Home
Kiswahili
Precalculus (OpenStax)
12: Utangulizi wa Calculus
12.1: Kupata Mipaka - Njia za Nambari na za kielelezo

12.1: Kupata Mipaka - Njia za Nambari na za kielelezo

Last updated
Save as PDF

Page ID: 181320

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Intuitively, tunajua kikomo ni nini. Gari linaweza kwenda kwa haraka sana na hakuna kasi. Takataka inaweza kushikilia 33 galoni na hakuna zaidi. Ni kawaida kwa kiasi cha kipimo kuwa na mipaka. Nini, kwa mfano, ni kikomo cha urefu wa mwanamke? Mwanamke mrefu zaidi katika rekodi alikuwa Jinlian Zeng kutoka China, ambaye alikuwa 8 ft 1 katika. ¹ Je, hii ni kikomo cha urefu ambao wanawake wanaweza kukua? Labda si, lakini kuna uwezekano kikomo tuweze kuelezea katika inchi kama tulikuwa na uwezo wa kuamua nini ilikuwa.

Ili kuiweka hesabu, kazi ambayo pembejeo yake ni mwanamke na ambaye pato lake ni urefu wa kipimo katika inchi ina kikomo. Katika sehemu hii, tutachunguza mbinu za namba na za kielelezo za kutambua mipaka.

Kuelewa Nukuu ya Kikomo

Tumeona jinsi mlolongo unaweza kuwa na kikomo, thamani kwamba mlolongo wa maneno hatua kuelekea kama nu mber ya suala kuongezeka. Kwa mfano, suala la mlolongo

\[1,\dfrac{1}{2},\dfrac{1}{4},\dfrac{1}{8}... \nonumber \]

anapata karibu na karibu na 0. Mlolongo ni aina moja ya kazi, lakini kazi ambazo si Utaratibu zinaweza pia kuwa na mipaka. Tunaweza kuelezea tabia ya kazi kama maadili pembejeo kupata karibu na thamani maalum. Ikiwa kikomo cha kazi$f(x)=L$, basi kama pembejeo$x$ inapata karibu na karibu na$a$, pato y -kuratibu anapata karibu na karibu na$L$. Tunasema kwamba pato “mbinu”$L$.

Kielelezo$\PageIndex{1}$ hutoa uwakilishi Visual ya dhana ya hisabati ya kikomo. Kama thamani ya pembejeo$x$ inakaribia$a$, thamani ya pato$f(x)$ inakaribia L.

Kielelezo$\PageIndex{1}$: Pato (y -kuratibu) mbinu$L$ kama pembejeo (x -kuratibu) mbinu$a$.

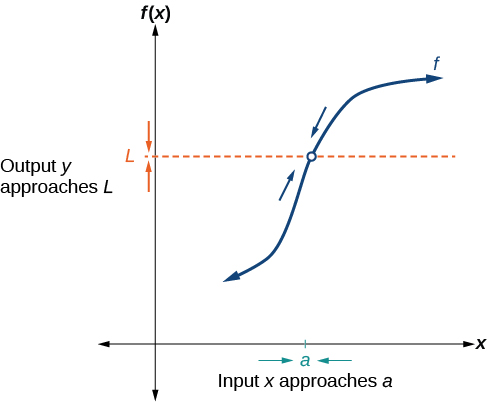
Tunaandika equation ya kikomo kama

\[\lim_{x \to a} f(x)=L. \nonumber \]

Uthibitisho huu unaonyesha kwamba, kama$x$ njia$a$ zote mbili kutoka upande wa kushoto$x=a$ na haki ya thamani$x=a,$ ya pato, mbinu.$L.$

Fikiria kazi

\[f(x)=\dfrac{x^2−6x−7}{x−7}. \label{eq1}\]

Tunaweza sababu kazi katika Equation\ ref {eq1} kama inavyoonekana.

\[\begin{array}{ll} f(x)=\dfrac{\cancel{(x−7)}(x+1)}{\cancel{x−7}} & \text{Cancel like factors in numerator and denominator.} \\ f(x)=x+1,x≠7 & \text{Simplify.} \end{array} \nonumber \]

Angalia kwamba$x$ haiwezi kuwa 7, au tungegawanyika kwa 0, hivyo 7 haipo katika uwanja wa kazi katika Equation\ ref {eq1}. Ili kuepuka kubadilisha kazi wakati sisi kurahisisha, sisi kuweka hali hiyo$x≠7$,, kwa kazi rahisi. Tunaweza kuwakilisha kazi graphically kama inavyoonekana katika Kielelezo$\PageIndex{2}$.

Kielelezo$\PageIndex{2}$: Kwa sababu 7 hairuhusiwi kama pembejeo, hakuna uhakika katika$x=7$.

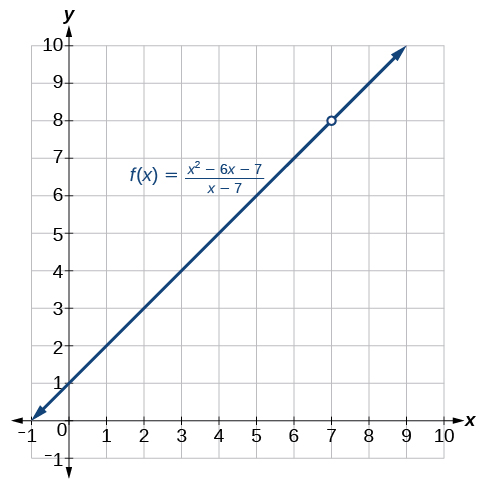
Kinachotokea$x=7$ ni tofauti kabisa na kile kinachotokea$x=7$ kwenye pointi karibu na upande wowote. Nukuu

\[\lim_{x \to 7} f(x)=8 \nonumber \]

inaonyesha kwamba kama pembejeo$x$ inakaribia 7 kutoka upande wa kushoto au wa kulia, pato linakaribia 8. Pato linaweza kupata karibu na 8 kama tunavyopenda ikiwa pembejeo iko karibu na 7.

Ni nini kinachotokea$x=7$? Wakati$x=7$, hakuna pato sambamba. Tunaandika hii kama

\[f(7) \text{does not exist.} \nonumber \]

Uthibitisho huu unaonyesha kwamba 7 haipo katika uwanja wa kazi. Tulikuwa tayari unahitajika hii wakati sisi aliandika kazi kama

\[f(x)=x+1, x≠7. \nonumber \]

Kumbuka kwamba kikomo cha kazi inaweza kuwepo hata wakati$f(x)$ si defined katika$x=a.$ Mengi ya kazi yetu baadae itakuwa kuamua mipaka ya kazi kama$x$$a$ inakaribia, hata kama pato katika$x=a$ haipo.

KIKOMO CHA KAZI

Wingi$L$ ni kikomo cha kazi$f(x)$ kama$x$ mbinu kama,$a$ kama maadili ya pembejeo ya$x$ mbinu$a$ (lakini si sawa$a$), maadili sambamba pato ya$f(x)$ kupata karibu na$L$. Kumbuka kuwa thamani ya kikomo haiathiriwa na thamani ya pato la$f(x)$ saa$a$. Wote$a$ na$L$ lazima iwe namba halisi. Tunaandika kama

\[ \lim_{x \to a} f(x)=L \nonumber \]

Mfano$\PageIndex{1}$: Understanding the Limit of a Function

Kwa kikomo zifuatazo, kufafanua$a,f(x),$ na$L.$

\[ \lim_{x \to 2} (3x+5)=11 \nonumber \]

Suluhisho

Kwanza, tunatambua nukuu ya kikomo. Kama kikomo ipo, kama$x$ mbinu$a$, sisi kuandika

\[ \lim_{x \to a} f(x)=L. \nonumber \]

Tunapewa

\[ \lim_{x \to 2} (3x+5)=11. \nonumber \]

Hii ina maana kwamba$a=2,f(x)=3x+5,$ na$L=11.$

Uchambuzi

Kumbuka kwamba$y=3x+5$ ni mstari na mapumziko hakuna. Kama maadili ya pembejeo yanakaribia 2, maadili ya pato yatapata karibu na 11. Hii inaweza kuwa phrased na equation$ \lim_{x \to 2}(3x+5)=11,$ ambayo ina maana kwamba kama$x$ inakaribia 2 (lakini si hasa 2), pato la kazi$f(x)=3x+5$ anapata karibu kama tunataka$3(2)+5,$ au$11$, ambayo ni kikomo$L$, kama sisi kuchukua maadili ya$x$ kutosha karibu 2 lakini si katika $x=2$.

Zoezi$\PageIndex{1}$

Kwa kikomo kinachofuata, kufafanua$a,f(x)$, na$L$.

\[ \lim_{x \to 5} (2x^2 −4)=46 \nonumber \]

Suluhisho

$a=5, f(x)=2x^2−4,$na$L=46.$

Kuelewa Mipaka ya Mkono wa Kushoto na Mipaka

Tunaweza mbinu pembejeo ya kazi kutoka upande wa thamani - kutoka kushoto au kulia. Kielelezo$\PageIndex{3}$ inaonyesha maadili ya

\[f(x)=x+1,x≠7 \nonumber \]

kama ilivyoelezwa hapo awali na taswira katika Kielelezo$\PageIndex{3}$.

Kielelezo$\PageIndex{3}$ ni$6.9, 6.99,$ na$6.999$. matokeo sambamba ni$7.9,7.99,$ na maadili$7.999.$ haya ni kupata karibu na 8. Kikomo cha maadili ya$f(x)$ kama$x$ mbinu kutoka upande wa kushoto inajulikana kama kikomo cha mkono wa kushoto. Kwa kazi hii, 8 ni kikomo cha mkono wa kushoto wa kazi$f(x)=x+1,x≠7$ kama$x$ mbinu 7.

Maadili ilivyoelezwa kama “kutoka kulia” ni kubwa kuliko thamani ya pembejeo 7 na kwa hiyo itaonekana na haki ya thamani kwenye mstari wa namba. maadili pembejeo kwamba mbinu 7 kutoka kulia katika Kielelezo$\PageIndex{3}$ ni$7.1, 7.01, $ na$7.001.$ matokeo sambamba ni$8.1, 8.01,$ na maadili$8.001.$ haya ni kupata karibu na 8. Kikomo cha maadili ya$f(x)$ kama$x$ mbinu kutoka kulia inajulikana kama kikomo cha mkono wa kulia. Kwa kazi hii, 8 pia ni kikomo cha mkono wa kulia wa kazi$f(x)=x+1,x≠7$ kama$x$ mbinu 7.

Kielelezo$\PageIndex{3}$ kinaonyesha kwamba tunaweza kupata pato la kazi ndani ya umbali wa 0.1 kutoka 8 kwa kutumia pembejeo ndani ya umbali wa 0.1 kutoka 7. Kwa maneno mengine, tunahitaji pembejeo$x$ ndani ya muda$6.9<x<7.1$ ili kuzalisha thamani ya pato ya$f(x)$ ndani ya muda$7.9<f(x)<8.1.$

Pia tunaona kwamba tunaweza kupata maadili ya pato ya$f(x)$ mfululizo karibu na 8 kwa kuchagua maadili ya pembejeo karibu na 7. Kwa kweli, tunaweza kupata maadili ya pato ndani ya muda wowote maalum kama sisi kuchagua maadili sahihi pembejeo.

Kielelezo$\PageIndex{4}$ hutoa uwakilishi Visual ya kushoto- na haki ya mipaka ya kazi. Kutoka grafu ya$f(x)$, tunaona pato inaweza kupata infinitesimally karibu na$L=8$ kama$x $ mbinu 7 kutoka kushoto na kama$x$ mbinu 7 kutoka kulia.

Ili kuonyesha kikomo cha mkono wa kushoto, tunaandika

\[ \lim_{x \to 7^−} f(x)=8. \nonumber \]

Ili kuonyesha kikomo cha mkono wa kulia, tunaandika

\[\lim_{x \to 7^+} f(x)=8. \nonumber \]

Kielelezo$\PageIndex{4}$: kushoto- na kulia mipaka ni sawa kwa ajili ya kazi hii.

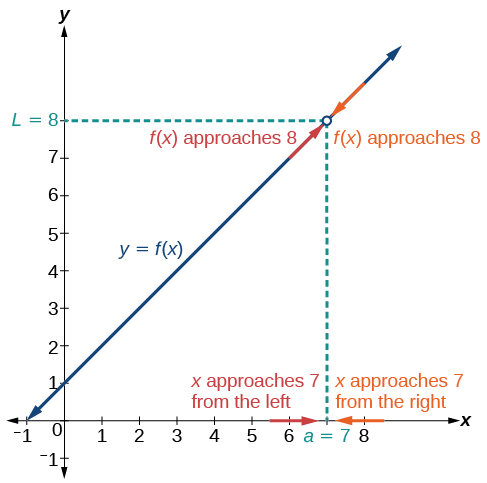
MIPAKA YA KUSHOTO NA MKONO WA KULIA

Kikomo cha mkono wa kushoto cha kazi$f(x)$ kama$x$ mbinu$a$ kutoka upande wa kushoto ni sawa na$L$, iliyoashiria\[\lim_{x \to a^−}f(x)=L. \nonumber \]

Maadili ya$f(x)$ yanaweza kupata karibu na kikomo$L$ kama tunavyopenda kwa kuchukua maadili ya$x$ kutosha karibu na$a$ vile vile$x<a$ na$x≠a.$

Kikomo cha mkono wa kulia wa kazi$f(x),$ kama$x$ mbinu$a$ kutoka kwa haki, ni sawa na$L,$ kutajwa na\[ \lim_{x \to a^+} f(x)=L. \nonumber \]

Maadili ya$f(x)$ yanaweza kupata karibu na kikomo$L$ kama tunavyopenda kwa kuchukua maadili ya$x$ kutosha karibu$a$ lakini zaidi kuliko$a$. Wote$a$ na$L$ ni idadi halisi.

Kuelewa Mipaka miwili

Katika mfano uliopita, kikomo cha mkono wa kushoto na kikomo cha mkono wa kulia kama$x$ mbinu$a$ ni sawa. Kama kushoto- na haki ya mipaka ni sawa, tunasema kwamba kazi$f(x)$ ina kikomo mbili upande mmoja kama$x $ mbinu$a.$ Zaidi ya kawaida, sisi tu rejea kikomo mbili upande mmoja kama kikomo. Ikiwa kikomo cha mkono wa kushoto haufanani na kikomo cha mkono wa kulia, au ikiwa mmoja wao haipo, tunasema kikomo haipo.

Kikomo cha kazi$f(x)$, kama$x$ mbinu$a$, ni sawa na$L$, yaani,\[ \lim_{x \to a} f(x)=L \nonumber \] ikiwa na tu ikiwa\[\lim_{x \to a^−} f(x)= \lim_{x \to a^+} f(x). \nonumber \]

Kwa maneno mengine, kikomo cha mkono wa kushoto wa kazi$f(x)$ kama$x$ mbinu$a$ ni sawa na kikomo cha mkono wa kulia wa kazi sawa na$x$ mbinu$a.$ Ikiwa kikomo hicho kipo, tunarejelea kikomo kama kikomo cha upande mmoja. Vinginevyo tunasema kikomo haipo.

Kutafuta Kikomo Kutumia Grafu

Kwa kuibua kuamua kama kikomo ipo kama$x$ mbinu$a$, tunaona grafu ya kazi wakati$x$ ni karibu sana na$x=a.$ Katika Kielelezo$\PageIndex{5}$ tunaona tabia ya grafu pande zote mbili za a.

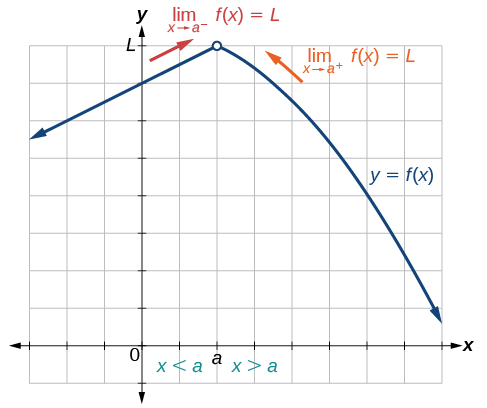
Kuamua kama kikomo cha mkono wa kushoto kipo, tunaona tawi la grafu upande wa kushoto$x=a$, lakini karibu$x=a$. Hapa ndipo$x<a.$ Tunaona kwamba matokeo ni kupata karibu na baadhi ya idadi halisi$L$ hivyo kuna kikomo mkono wa kushoto.

Kuamua kama kikomo cha mkono wa kulia kipo, angalia tawi la grafu kwa haki ya$x=a,$ lakini karibu$x=a$. Hii ndio wapi$x>a$. Tunaona kwamba matokeo ni kupata karibu na baadhi ya idadi halisi$L$, hivyo kuna kikomo haki mkono.

Ikiwa kikomo cha mkono wa kushoto na kikomo cha mkono wa kulia ni sawa, kama ilivyo kwenye Mchoro$\PageIndex{5}$, basi tunajua kwamba kazi ina kikomo cha upande mmoja. Kwa kawaida, tunapotaja “kikomo,” tunamaanisha kikomo cha upande mmoja, isipokuwa tukiiita kikomo cha upande mmoja.

Hatimaye, tunaweza kuangalia kwa thamani pato kwa ajili ya kazi$f(x)$ wakati thamani pembejeo$x$ ni sawa na$a$. Jozi ya kuratibu ya uhakika itakuwa$(a,f(a)).$ Kama hatua hiyo ipo, basi$f(a)$ ina thamani. Ikiwa hatua haipo, kama ilivyo kwenye Kielelezo$\PageIndex{5}$, basi tunasema kwamba$f(a)$ haipo.

JINSI YA: Kutokana na kazi$f(x)$, use a graph to find the limits and a function value as $x$ approaches $a.$

Kuchunguza grafu ili uone kama kikomo cha mkono wa kushoto kipo.
Kuchunguza grafu ili uone kama kikomo cha mkono wa kulia kipo.
Ikiwa mipaka miwili ya upande mmoja iko na ni sawa, basi kuna kikomo cha upande mbili-kile tunachokiita “kikomo.”
Kama kuna uhakika katika$x=a,$ basi$f(a)$ ni sambamba kazi thamani.

Mfano$\PageIndex{2}$: Finding a Limit Using a Graph

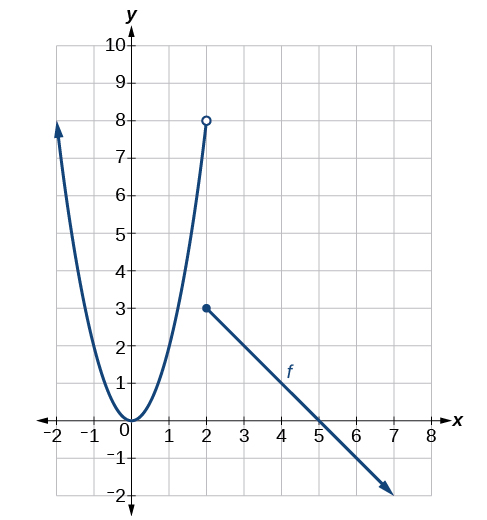
Kuamua mipaka ifuatayo na thamani ya kazi kwa ajili ya kazi$f$ inavyoonekana katika Kielelezo$\PageIndex{6}$.

$ \lim_{x \to 2^−} f(x)$
$ \lim_{x \to 2^+} f(x)$
$ \lim_{x \to 2} f(x)$
$f(2)$

Kuamua mipaka ifuatayo na thamani ya kazi kwa ajili ya kazi f f inavyoonekana katika Kielelezo.

$ \lim_{x \to 2^−} f(x)$
$ \lim_{x \to 2^+} f(x)$
$ \lim_{x \to 2} f(x)$
$f(2)$

Kuangalia Kielelezo:
1. $\lim_{x \to 2^−} f(x)=8; $wakati$x<2$, lakini infinitesimally karibu na 2, maadili ya pato kupata karibu na$y=8$.
2. $ \lim_{x \to 2^+} f(x)=3;$wakati$x>2$, lakini infinitesimally karibu na 2, maadili ya pato mbinu$y=3$.
3. $ \lim_{x \to 2} f(x)$haipo kwa sababu mipaka$ \lim_{x \to 2 ^−} f(x)≠ \lim_{x \to 2^+} f(x);$ ya kushoto na ya kulia si sawa.
4. $f(2)=3$kwa sababu grafu ya kazi$f$ inapita kupitia hatua$(2,f(2))$ au$(2,3).$
Kuangalia Kielelezo:
1. $\lim_{x \to 2^−} f(x)=8; $wakati$x<2$ lakini infinitesimally karibu na 2, maadili ya pato mbinu$y=8.$
2. $\lim_{x \to 2^+} f(x)=8; $wakati$x>2$ lakini infinitesimally karibu na 2, maadili ya pato mbinu$y=8$.
3. $\lim_{x \to 2} f(x)=8; $$ \lim_{x \to 2^−} f(x)= \lim_{x \to 2^+} f(x)=8;$kwa sababu mipaka ya kushoto na ya kulia ni sawa.
4. $f(2)=4$kwa sababu grafu ya kazi$f$ hupita kupitia hatua$(2,f(2))$ au$(2,4)$.

Zoezi$\PageIndex{2}$:

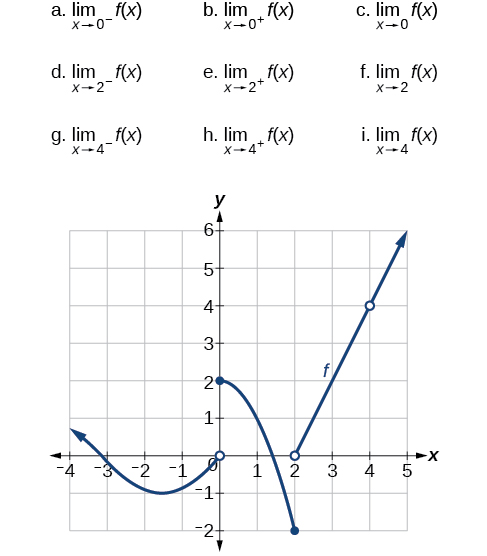
Kutumia grafu ya kazi y=f (x) y=f (x) iliyoonyeshwa kwenye Kielelezo, tathmini mipaka ifuatayo.

$Grafu ya kazi piecewise ambayo ina makundi matatu: 1) infinity hasi kwa 0, 2) kwa 2, na 3) 2 kwa infinity chanya, ambayo ina discontinuity katika (4, 4)$

Suluhisho

a. 0; b. 2; c. haipo; d.-1; -2; e. 0; f. haipo; g. 4; h. 4; i. 4

Kutafuta Kikomo Kutumia Jedwali

Kujenga meza ni njia ya kuamua mipaka kwa kutumia habari za nambari. Tunaunda meza ya maadili ambayo maadili ya pembejeo ya$x$ mbinu$a$ kutoka pande zote mbili. Kisha tunaamua ikiwa maadili ya pato yanakaribia na karibu na thamani halisi, kikomo$L$.

Hebu fikiria mfano kwa kutumia kazi ifuatayo:

\[ \lim_{x \to 5} \left( \dfrac{x^3−125}{x−5} \right) \nonumber \]

Ili kuunda meza, tunatathmini kazi kwa maadili karibu na$x=5$. Sisi kutumia baadhi ya maadili pembejeo chini ya 5 na baadhi ya maadili zaidi ya 5 kama katika Kielelezo. Maadili ya meza yanaonyesha kwamba wakati$x>5$ lakini inakaribia 5, pato linalofanana linapata karibu na 75. Wakati$x>5$ lakini inakaribia 5, pato linalofanana pia linapata karibu na 75.

$CNX_Precalc_Figure_12_01_008n.jpg$

Kwa sababu

\[\lim_{x \to 5^−} f(x)=75= \lim_{x \to 5^+} f(x), \nonumber \]

basi

\[ \lim_{x \to 5} f(x)=75. \nonumber \]

Kumbuka kwamba$f(5)$ haipo.

Jinsi ya: Kutokana na kazi$f$,use a table to find the limit as $x$ approaches $a$ and the value of $f(a)$, if it exists.

Chagua maadili kadhaa ya pembejeo ambayo inakaribia a kutoka upande wa kushoto na wa kulia. Rekodi yao katika meza.
Tathmini kazi katika kila thamani ya pembejeo. Rekodi yao katika meza.
Tambua ikiwa maadili ya meza yanaonyesha kikomo cha mkono wa kushoto na kikomo cha mkono wa kulia.
Ikiwa mipaka ya mkono wa kushoto na wa kulia iko na ni sawa, kuna kikomo cha upande mmoja.
Badilisha nafasi$x$ na$a$ kupata thamani ya$f(a)$.

Mfano$\PageIndex{3}$: Finding a Limit Using a Table

Ukadiria kwa kiasi kikubwa kikomo cha maneno yafuatayo kwa kuanzisha meza ya maadili pande zote mbili za kikomo.

\[\lim_{x \to 0} \left( \dfrac{5 \sin(x)}{3x} \right) \nonumber \]

Suluhisho

Tunaweza kukadiria thamani ya kikomo, kama ipo, kwa kutathmini kazi katika maadili karibu$x=0$. Hatuwezi kupata thamani ya kazi kwa$x=0$ moja kwa moja kwa sababu matokeo yatakuwa na denominator sawa na 0, na hivyo itakuwa haijulikani.

\[ f(x)= \dfrac{5 \sin (x)}{3x} \nonumber \]

Sisi kujenga Kielelezo kwa kuchagua maadili kadhaa pembejeo karibu$x=0,$ na nusu yao chini ya$x=0$ na nusu yao kubwa kuliko$x=0.$ Kumbuka kwamba tunahitaji kuwa na uhakika sisi ni kutumia mode radian. Tunatathmini kazi katika kila thamani ya pembejeo ili kukamilisha meza.

Maadili ya meza yanaonyesha kwamba wakati$x<0$ lakini inakaribia 0, pato linalofanana linakaribia$\frac{5}{3}.$

Wakati$x>0$ lakini inakaribia 0, pato sambamba pia inakaribia$\frac{5}{3}.$

$CNX_Precalc_Figure_12_01_009.jpg$

Kwa sababu

\[ \lim_{x \to 0^−} f(x)=\dfrac{5}{3} = \lim_{x \to 0^+} f(x), \nonumber \]

basi

\[\lim_{x \to 0} f(x)=\dfrac{5}{3}. \nonumber \]

Swali & A: Inawezekana kuangalia jibu letu kwa kutumia matumizi ya graphing?

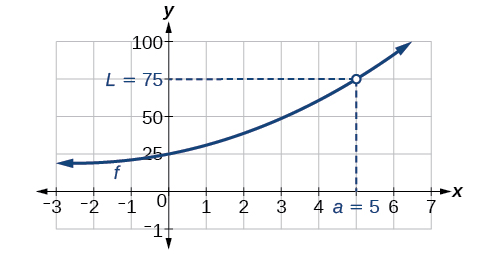
Ndiyo. Sisi hapo awali kutumika meza ya kupata kikomo cha 75 kwa ajili ya kazi $f(x)=\frac{x^3−125}{x−5}$kama$x$ mbinu 5. Kuangalia, sisi grafu kazi kwenye dirisha la kutazama kama inavyoonekana kwenye Kielelezo. Cheti cha picha kinaonyesha matawi yote ya grafu ya kazi kupata karibu na pato 75 kama$x$ inakaribia 5. Zaidi ya hayo, tunaweza kutumia kipengele cha 'kufuatilia' cha calculator ya graphing. By inakaribia$x=5$ tunaweza numerically kuchunguza matokeo sambamba kupata karibu na 75.

$CNX_Precalc_Figure_12_01_010F.jpg$

Zoezi$\PageIndex{3}$:

Kwa kiasi kikubwa kukadiria kikomo cha kazi ifuatayo kwa kufanya meza:

\[ \lim_{x \to 0} \left( \dfrac{20 \sin (x)}{4x} \right) \nonumber \]

Suluhisho

\[ \lim_{x \to 0} \left( \dfrac{20 \sin (x)}{4x} \right) = 5 \nonumber \]

$CNX_Precalc_Figure_12_01_014.jpg$

Q & A

Je, njia moja ya kuamua kikomo bora kuliko nyingine?

Hapana. Njia zote mbili zina faida. Graphing inaruhusu ukaguzi wa haraka. Majedwali yanaweza kutumika wakati huduma za graphical hazipatikani, na zinaweza kuhesabiwa kwa usahihi wa juu kuliko inaweza kuonekana kwa jicho lisilosaidiwa kuchunguza grafu.

Mfano$\PageIndex{4}$: Using a Graphing Utility to Determine a Limit

Kwa matumizi ya matumizi ya graphing, ikiwa inawezekana, tambua mipaka ya kushoto na ya kulia ya kazi ifuatayo kama$x$ mbinu 0. Kama kazi ina kikomo kama$x$ mbinu 0, hali yake. Ikiwa sio, jadili kwa nini hakuna kikomo.

\[f(x)=3 \sin (\dfrac{π}{x}) \nonumber \]

Suluhisho

Tunaweza kutumia matumizi ya graphing kuchunguza tabia ya grafu karibu na$x=0$. Kuzunguka karibu$x=0,$ tunachagua madirisha mawili ya kutazama kama vile ya pili imefungwa karibu na$x=0$ ya kwanza. Matokeo yake yanafanana Kielelezo$[−2,2]$ kwa na$[−3,3]$.

Figure_12_01_012">Kielelezo$[−0.1,0.1]$ kwa$[−3,3]$.

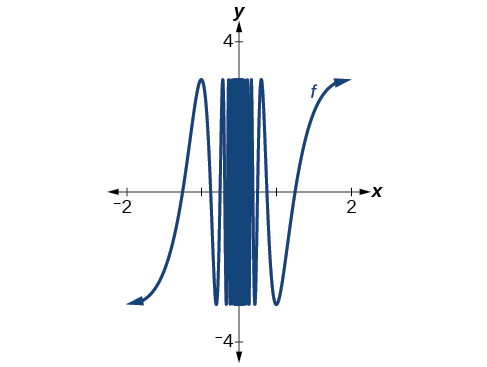
Hata karibu na sifuri, sisi ni hata chini ya uwezo wa kutofautisha mipaka yoyote.

Karibu tunapata 0, zaidi ya swings katika maadili ya pato ni. Hiyo sio tabia ya kazi na kikomo cha mkono wa kushoto au kikomo cha mkono wa kulia. Na kama hakuna kikomo cha mkono wa kushoto au kikomo cha mkono wa kulia, hakika hakuna kikomo kwa kazi$f(x)$ kama$x$ mbinu 0.

Tunaandika

\[ \lim_{x \to 0^−} \left( 3 \sin \left( \dfrac{π}{x} \right) \right) \;\;\; \text{does not exist.} \nonumber \]

\[ \lim_{x \to 0^+} \left( 3 \sin \left( \dfrac{π}{x} \right) \right) \;\;\; \text{does not exist.} \nonumber \]

\[ \lim_{x \to 0} \left( 3 \sin \left( \dfrac{π}{x} \right) \right) \;\;\; \text{does not exist.} \nonumber \]

Zoezi$\PageIndex{4}$:

Numerically makisio kikomo zifuatazo:$ \lim \limits_{x \to 0} (\sin (\frac{2}{x}))$.

Suluhisho

haipo

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kupata mipaka.

Dhana muhimu

kazi ina kikomo kama maadili pato mbinu baadhi ya thamani$L$ kama maadili pembejeo mbinu baadhi ya kiasi a. tazama mfano.
Notation shorthand hutumiwa kuelezea kikomo cha kazi kulingana na fomu$ \lim \limits_{x \to a} f(x)=L,$ ambayo inaonyesha kuwa kama$x$ mbinu$a$, wote kutoka kushoto$x=a$ na haki ya thamani$x=a,$ ya pato anapata karibu na$L.$
kazi ina kikomo mkono wa kushoto kama$f(x)$ mbinu$L$ kama$x$ mbinu$x<a.$ a ambapo kazi ina kikomo haki mkono kama$f(x)$ mbinu$L$ kama$x$ mbinu$a$ ambapo$x>a$.
Kikomo cha upande mmoja kipo ikiwa kikomo cha mkono wa kushoto na kikomo cha mkono wa kulia cha kazi ni sawa. Kazi inasemekana kuwa na kikomo ikiwa ina kikomo cha upande mmoja.
Grafu hutoa njia ya kuona ya kuamua kikomo cha kazi.
Ikiwa kazi ina kikomo kama$x$ mbinu$a$, matawi ya grafu yatakaribia$y-$ kuratibu sawa karibu$x=a$ na kushoto na kulia. Angalia Mfano.
Jedwali linaweza kutumika kuamua kama kazi ina kikomo. Jedwali linapaswa kuonyesha maadili ya pembejeo ambayo yanakaribia$a$ kutoka kwa maelekezo yote ili maadili ya pato yanaweza kupimwa. Ikiwa maadili ya pato yanakaribia nambari fulani, kazi ina kikomo. Angalia Mfano.
Huduma ya graphing pia inaweza kutumika kupata kikomo. Angalia Mfano.

maelezo ya chini

1 https://en.Wikipedia.org/wiki/Human_height na http://en.Wikipedia.org/wiki/List_of_tallest_people

faharasa

kikomo cha mkono wa kushoto: kikomo cha maadili ya$f(x) \nonumber $ kama$x$ mbinu kutoka upande$a$ wa kushoto, ulionyehsa\[\lim \limits_{x \to a^−} f(x)=L. \nonumber \] Maadili ya$f(x) \nonumber $ yanaweza kupata karibu na kikomo$L$ kama tunavyopenda kwa kuchukua maadili ya$x$ kutosha karibu na kama hiyo$x<a \nonumber $ na $x≠a. \nonumber $. Wote$a$ na$L$ ni idadi halisi.

kikomo: wakati ipo, thamani$L$, kwamba pato la kazi$f(x)$ mbinu kama pembejeo$x$ anapata karibu na karibu na$a$ lakini si sawa$a$. Thamani ya pato,$f(x), \nonumber $ inaweza kupata karibu na$L$ tunapochagua kuifanya kwa kutumia maadili ya pembejeo ya$x$ kutosha karibu na$x=a$, lakini sio lazima$x=a$. Wote wawili$a$ na$L$ ni idadi halisi, na$L$ ni ulionyehsa\[\lim \limits_{x \to a}f(x)=L. \nonumber \]

kikomo cha mkono wa kulia: kikomo cha maadili ya$f(x)$ kama$x$ mbinu$a$ kutoka kulia, inaashiria Maadili\[\lim \limits_{x \to a^+}f(x)=L. \nonumber \] ya$f(x)$ yanaweza kupata karibu na kikomo$L$ kama tunavyopenda kwa kuchukua maadili ya$x$ kutosha karibu na$a$ wapi $x>a,$ na$x≠a.$ Wote wawili$a$ na$L$ ni idadi halisi.

kikomo cha upande mmoja: kikomo cha kazi\[f(x), \nonumber \] kama$x$ mbinu$a$, ni sawa na$L$, yaani,\[\lim \limits_{x \to a} f(x)=L \nonumber \] kama na tu kama\[\lim \limits_{x \to a^−} f(x)= \lim \limits_{x \to a^+}f(x). \nonumber \]