7.2: Utambulisho wa Jumla na Tofauti
- Page ID
- 181507
- Tumia jumla na tofauti formula kwa cosine.
- Matumizi jumla na tofauti formula kwa sine.
- Tumia jumla na tofauti formula kwa tangent.
- Tumia jumla na tofauti formula kwa cofunctions.
- Tumia jumla na tofauti formula ili kuthibitisha utambulisho.
Urefu wa mlima unaweza kupimwaje? Nini kuhusu umbali kutoka Dunia hadi jua? Kama matatizo mengi yanayoonekana haiwezekani, tunategemea kanuni za hisabati ili kupata majibu. Utambulisho wa trigonometric, unaotumiwa kwa kawaida katika ushahidi wa hisabati, umekuwa na maombi halisi ya ulimwengu kwa karne nyingi, ikiwa ni pamoja na matumizi yao katika kuhesabu umbali mrefu.
Utambulisho wa trigonometric tutachunguza katika sehemu hii unaweza kufuatiliwa na mwanaastronomia wa Kiajemi ambaye aliishi karibu 950 AD, lakini Wagiriki wa kale waligundua kanuni hizi sawa mapema na kuzielezea kwa suala la chords. Hizi ni equations maalum au postulates, kweli kwa maadili yote pembejeo kwa equations, na kwa maombi yasiyo na idadi.

Katika sehemu hii, tutajifunza mbinu ambazo zitatuwezesha kutatua matatizo kama vile yale yaliyotolewa hapo juu. Fomu zinazofuata zitapunguza maneno mengi ya trigonometric na equations. Kumbuka kwamba, katika sehemu hii, fomu ya neno hutumiwa sawa na utambulisho wa neno.
Kutumia Fomu za Jumla na Tofauti kwa Cosine
Kupata thamani halisi ya sine, cosine, au tangent ya angle mara nyingi ni rahisi kama tunaweza kuandika upya angle iliyotolewa kwa suala la pembe mbili ambazo zinajulikana maadili ya trigonometric. Tunaweza kutumia pembe maalum, ambayo tunaweza kupitia katika mduara kitengo inavyoonekana katika Kielelezo\(\PageIndex{2}\).
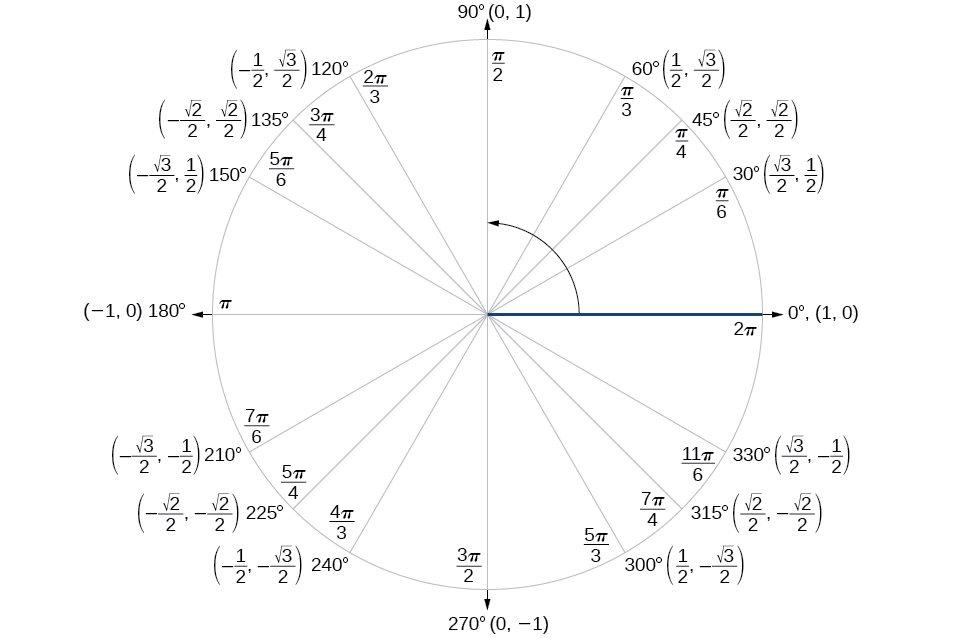
Tutaanza na kanuni za jumla na tofauti za cosine, ili tuweze kupata cosine ya angle iliyotolewa ikiwa tunaweza kuivunja ndani ya jumla au tofauti ya pembe mbili maalum (Jedwali\(\PageIndex{1}\)).
| Fomu ya jumla ya cosine | \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\) |
| Fomu tofauti ya cosine | \(\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
Kwanza, tutaonyesha formula tofauti kwa cosines. Hebu fikiria pointi mbili kwenye mduara wa kitengo (Kielelezo\(\PageIndex{3}\)). Point\(P\) ni kwa pembe\(\alpha\) kutoka kwa\(x\) mhimili mzuri na kuratibu\((\cos \alpha,\sin \alpha)\) na uhakika\(Q\) ni pembe ya\(\beta\) kutoka kwa mhimili mzuri\(x\) na kuratibu\((\cos \beta,\sin \beta)\). Kumbuka kipimo cha angle\(POQ\) ni\(\alpha−\beta\).
Weka alama mbili zaidi: kwa\(A\) pembe ya\((\alpha−\beta)\) kutoka kwa mhimili mzuri\(x\) na kuratibu\((\cos(\alpha−\beta),\sin(\alpha−\beta))\); na ueleze\(B\) na kuratibu\((1,0)\). Triangle\(POQ\) ni mzunguko wa pembetatu\(AOB\) na hivyo umbali kutoka\(P\) kwa\(Q\) ni sawa na umbali kutoka\(A\) kwa\(B\).
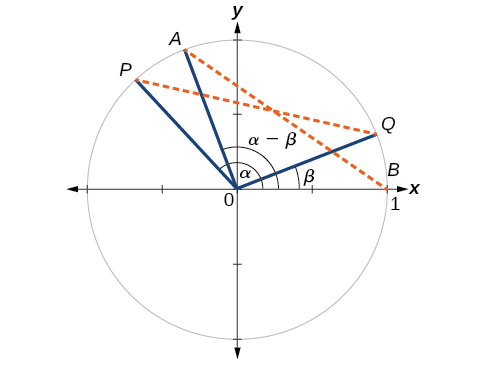
Tunaweza kupata umbali kutoka kwa\(P\)\(Q\) kutumia formula ya umbali.
\ [kuanza {align*}
d_ {PQ} &=\ sqrt {{(\ cos\ alpha -\ cos\ beta)} ^2+ {(dhambi\ alpha - dhambi\ beta)} ^2}\\ [4pt]
&=\ sqrt {\ cos} ^2\ alpha-2\ cos\\ alpha\ beta+ {\ cos} ^2\ beta+ dhambi} ^2\ alpha-2\ dhambi\ alpha\ dhambi\ beta+ {\ dhambi} ^2\ beta} & &\ maandishi {Weka utambulisho wa Pythagorean na kurahisisha.}\\ [4pt]
&=\ sqrt {({\ cos} ^2\ alpha+ {\ dhambi} ^2\ alpha) + ({\ cos} ^2\ beta+ {\ dhambi} ^2\ beta) -2\ cos\ alpha\\ dhambi\ beta}\\ [4pt]
&=\ sqrt {1+1-2\ cos\ alpha\ cos\ beta-2\ dhambi\ alpha\ dhambi\ beta}\\ [4pt]
&=\ sqrt {2-2\ cos\ alpha\ cos\ beta-2\ dhambi\ alpha\ dhambi\ beta}\ mwisho {align*}\]
Vile vile, kwa kutumia formula ya umbali tunaweza kupata umbali kutoka\(A\) kwa\(B\).
\ [kuanza {kuungana*}
d_ {AB} &=\ sqrt {{(\ cos (\ alpha-\ beta) -1)} ^2+ {(\ dhambi (\ alpha-\ beta) -0)} ^2}\\ [4pt]
&=\ sqrt {{\ cos} ^2 (\ alpha-\ beta) -2\ cos (\ alpha-\ beta) +1+\ dhambi} ^2 (\ alpha-\ beta)} & &\ maandishi {Weka utambulisho wa Pythagorean na kurahisisha}\\ [4pt]
&=\ sqrt {({\ cos} ^2 (\ alpha-\ beta) + {\ dhambi} ^2 (\ alpha-\ beta) -2\ cos (\ alpha-\ beta) +1}\\ [4pt]
&=\ sqrt {1-2\ cos (\ alpha-\ beta) +1}\\ [4pt]
&=\ sqrt {2-2\ cos (\ alpha-\ beta)} & &\ maandishi {Ondoa 2 kutoka pande zote mbili na kugawanya pande zote mbili kwa -2.}\\ [4pt]
\ cos\ alpha\ cos\ beta+\ sin\ alpha\ dhambi\ beta&=\ cos (\ alpha-\ beta)
\ mwisho {align*}\]
Hivyo, tuna formula tofauti ya cosine. Tunaweza kutumia mbinu sawa ili kupata cosine ya jumla ya pembe mbili.
Fomu hizi zinaweza kutumika kuhesabu cosine ya jumla na tofauti za pembe.
\[\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\]
\[\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\]
- Andika formula tofauti ya cosine.
- Weka maadili ya pembe zilizopewa katika formula.
- Kurahisisha.
Kutumia formula ya cosine ya tofauti ya pembe mbili, pata thamani halisi ya\(\cos\left(\dfrac{5\pi}{4}−\dfrac{\pi}{6}\right)\).
Suluhisho
Anza kwa kuandika formula ya cosine ya tofauti ya pembe mbili. Kisha ubadilisha maadili yaliyotolewa.
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos\left(\dfrac{5\pi}{4}-\dfrac{\pi}{6}\right)&= \cos\left(\dfrac{5\pi}{4}\right)\cos\left(\dfrac{\pi}{6}\right)+\sin\left(\dfrac{5\pi}{4}\right)\sin\left(\dfrac{\pi}{6}\right)\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{\sqrt{3}}{2}\right)-\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{1}{2}\right)\\[4pt] &= -\dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{-\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Kumbuka kwamba tunaweza daima kuangalia jibu kwa kutumia calculator graphing katika mode radian.
Kupata thamani halisi ya\(\cos\left(\dfrac{\pi}{3}−\dfrac{\pi}{4}\right)\).
- Jibu
-
\(\dfrac{\sqrt{2}+\sqrt{6}}{4}\)
Kupata thamani halisi ya\(\cos(75°)\).
Suluhisho
Kama\(75°=45°+30°\), tunaweza kutathmini\(\cos(75°)\) kama\(\cos(45°+30°)\).
\[\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta -\sin \alpha \sin \beta\\[4pt] \cos(45^{\circ}+30^{\circ})&= \cos(45^{\circ})\cos(30^{\circ})-\sin(45^{\circ})\sin(30^{\circ})\\[4pt] &= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Kumbuka kwamba tunaweza daima kuangalia jibu kwa kutumia calculator graphing katika hali ya shahada.
Uchambuzi
Kumbuka kwamba tunaweza pia kutatuliwa tatizo hili kwa kutumia ukweli kwamba\( 75°=135°−60°\).
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos(135^{\circ}-60^{\circ})&= \cos(135^{\circ})\cos(60^{\circ})+\sin(135^{\circ})\sin(60^{\circ})\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{1}{2}\right)+\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= -\dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{6}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Kupata thamani halisi ya\(\cos(105°)\).
- Jibu
-
\(\dfrac{\sqrt{2}-\sqrt{6}}{4}\)
Kutumia Sum na Tofauti Formula kwa Sine
Fomu za jumla na tofauti za sine zinaweza kupatikana kwa njia sawa na zile za cosine, na zinafanana na kanuni za cosine.
Fomu hizi zinaweza kutumiwa kuhesabu sines ya jumla na tofauti za pembe.
\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]
\[\sin(\alpha−\beta)=\sin \alpha \cos \beta−\cos \alpha \sin \beta\]
- Andika formula tofauti kwa sine.
- Weka pembe zilizopewa katika formula.
- Kurahisisha.
Tumia utambulisho wa jumla na tofauti ili kutathmini tofauti ya pembe na kuonyesha kwamba sehemu a ni sawa na sehemu b.
- \(\sin(45°−30°)\)
- \(\sin(135°−120°)\)
Suluhisho
- Hebu tuanze kwa kuandika formula na ubadilishe pembe zilizopewa.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(45^{\circ}-30^{\circ})&= \sin(45^{\circ})\cos(30^{\circ})-\cos(45^{\circ})\sin(30^{\circ}) \end{align*}\]
Kisha, tunahitaji kupata maadili ya maneno ya trigonometric.
\(\sin(45°)=\frac{\sqrt{2}}{2}, \qquad \cos(30°)=\frac{\sqrt{3}}{2}, \qquad \cos(45°)=\frac{\sqrt{2}}{2}, \qquad \sin(30°)=\frac{1}{2}\)
Sasa tunaweza kubadilisha maadili haya katika equation na kurahisisha.
\[\begin{align*} \sin(45°-30°)&= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
- Tena, tunaandika formula na badala ya pembe zilizopewa.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(135^{\circ}-120^{\circ})&= \sin(135^{\circ})\cos(120^{\circ})-\cos(135^{\circ})\sin(120^{\circ}) \end{align*}\]
Kisha, tunapata maadili ya maneno ya trigonometric.
\(\sin(135°)=\frac{\sqrt{2}}{2}, \qquad \cos(120°)=-\frac{1}{2}, \qquad \cos(135°)=\frac{\sqrt{2}}{2}, \qquad \sin(120°)=\frac{\sqrt{3}}{2}\)
Sasa tunaweza kubadilisha maadili haya katika equation na kurahisisha.
\[\begin{align*} \sin(135^{\circ}-120^{\circ})&= \dfrac{\sqrt{2}}{2}\left(-\dfrac{1}{2}\right)-\left(-\dfrac{\sqrt{2}}{2}\right)\left (\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Kupata thamani halisi ya\(\sin\left ({\cos}^{−1}\frac{1}{2}+{\sin}^{−1}\frac{3}{5}\right)\). Kisha angalia jibu kwa calculator ya graphing.
Suluhisho
Mfano unaoonyeshwa katika tatizo hili ni\(\sin(\alpha+\beta)\). Hebu\(\alpha={\cos}^{−1}\frac{1}{2}\) na\(\beta={\sin}^{−1}\frac{3}{5}\). Basi tunaweza kuandika
\ [kuanza {align*}
\ cos\ alpha&=\ dfrac {1} {2},\ quad 0\ leq\ alpha\ leq\ pi\\ [4pt]
\ dhambi\ beta&=\ dfrac {3} {5},\ quad -\ dfrac {\ pi} {2}\ leq\ beta\ leq\ dfrac {\ pi} 2}\\[4pt]\end{align*}\]
Tutatumia utambulisho wa Pythagorean kupata\(\sin \alpha\) na\(\cos \beta\)
\ [kuanza {align*}
\ dhambi\ alpha&=\ sqrt {1- {\ cos} ^2\ alpha}\\ [4pt]
&=\ sqrt {1-\ dfrac {1} {4}}\\ [4pt]
&=\ [4pt]
&=\\ sqrt {\ sqrt {3}} {2}\\ [4pt]\ cos
\ beta&=\ sqrt {1- {\ dhambi} ^2\ beta}\\ [4pt]
& =\ sqrt {1-\ dfrac {9} {25}}\\ [4pt]
&=\ sqrt {\ dfrac {16} {25}}\ [4pt]
&=\ dfrac {4} {5}
\ mwisho {align*}\]
Kutumia formula jumla kwa sine,
\[\begin{align*} \sin \left({\cos}^{-1}\tfrac{1}{2}+{\sin}^{-1}\tfrac{3}{5}\right)&= \sin(\alpha+\beta)\\[4pt] &= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \dfrac{\sqrt{3}}{2}\cdot \dfrac{4}{5}+\dfrac{1}{2}\cdot \dfrac{3}{5}\\[4pt] &= \dfrac{4\sqrt{3}+3}{10} \end{align*}\]
Kutumia Fomu za Jumla na Tofauti kwa Tangent
Kupata maadili halisi kwa tangent ya jumla au tofauti ya pembe mbili ni ngumu zaidi, lakini tena, ni suala la kutambua mfano.
Kupata jumla ya pembe mbili formula kwa tangent inahusisha kuchukua quotient ya formula jumla kwa sine na cosine na kurahisisha. Kumbuka,\(\tan x=\dfrac{\sin x}{\cos x}\), wakati\(\cos x≠0\).
Hebu tupate fomu ya jumla ya tangent.
\ [kuanza {kuungana*}
\ tan\ kushoto (\ alpha+\ beta\ kulia) &=\ dfrac {\ dhambi\ kushoto (\ alpha+\ beta\ kulia)} {\ cos (\ alpha+\ beta)}\\ [6pt]
&=\ dfrac {\ sin\ alpha\ alpha\ cos\ beta-\ dhambi\ alpha\ sin\ beta}\\ [6pt]
&=\ dfrac {\ dfrac {\ dhambi\ alpha \\ cos\ beta+\ cos\ alpha\ sin\ beta} {\ cos\ alpha\ cos\ beta} {\ dfrac {\ cos\ alpha\ beta-\ dhambi\ alpha\ beta} {\ cos\ cos\\ beta}}\\ [6pt]
&=\ dfrac {\ dhambi\ alpha\ cos\ beta} {\ cos\ alpha\ alpha\ cos\ beta} +\ dfrac {\ cos\ alpha\ sin\ beta} {\ cos\ alpha\ cos\ beta}} {\ dfrac {\ cos\ alpha\ cos\ beta} {\ cos\ alpha\ cos\ beta} -\ dfrac {\ dhambi\ alpha\ sin\ beta} {\ cos\ alpha\ cos\ beta}\\ [6pt]
&=\ dfrac {\ dhambi\ alpha} {\ cos\ alpha} +\ dfrac {\ sin\ beta} {\ cos\ beta}} {\ cos\\ dfrac\ dhambi\ alpha\ dhambi\ beta} {\ cos\ alpha\ cos\ beta}}\\ [6pt]
&=\ dfrac {\ tan\ alpha+\ tan\ beta} {1-\ tan\ alpha\ tan\ beta}
\ mwisho {align*}\]
Tunaweza hupata tofauti formula kwa tangent kwa njia sawa.
Jumla na tofauti formula kwa tangent ni:
\[\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1−\tan \alpha \tan \beta}\]
\[\tan(\alpha-\beta)=\dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}\]
- Andika fomu ya jumla ya tangent.
- Weka pembe zilizopewa katika formula.
- Kurahisisha.
Kupata thamani halisi ya\(\tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)\).
Suluhisho
Hebu kwanza tuandike fomu ya jumla ya tangent na kisha ubadilishe pembe zilizopewa kwenye formula.
\ [kuanza {kuungana*}
\ tan (\ alpha+\ beta) &=\ dfrac {\ tan\ alpha+\ tan\ beta} {1-\ tan\ alpha\ tan\ beta}
\\ [4pt]\ tan\ kushoto (\ dfrac {\ pi} {\ pi} {4}\ haki) &=\ dfrac {\ tan {\ kushoto (\ dfrac {\ pi} {6}\ kulia) +\ tan\ kushoto (\ dfrac {\ pi} {4}\ kulia)} {1-\ kushoto (\ tan\ kushoto (\ dfrac {\ pi} {6}\ haki)\ kulia )\ kushoto (\ tan\ kushoto (\ dfrac {\ pi} {4}\ haki)\ haki)}\ mwisho {align*}\]
Kisha, tunaamua maadili ya kazi ya mtu binafsi ndani ya formula:
\[\tan\left (\dfrac{\pi}{6}\right )= \dfrac{1}{\sqrt{3}}, \quad \text{and} \quad \tan\left (\dfrac{\pi}{4}\right) = 1\]
Hivyo tuna,
\ [kuanza {\ pi}\ tan\ kushoto (\ dfrac {\ pi} {6} +\ dfrac {\ pi} {4}\ haki) &=\ dfrac {\ dfrac {1} {\ sqrt {3}} +1} {1-\ kushoto (\ dfrac {1} {\ sqrt {3}}\ haki) (1)}\\ [6pt]
&=\ dfrac {\ dfrac {1+\ sqrt {3}} {\ sqrt {3}}} {\ dfrac {\ sqrt {\ sqrt {3}}}\\ [6pt]
& amp; =\ dfrac {1+\ sqrt {3}} {\ sqrt {3}}\ dot\ dfrac {\ sqrt {3}} {\ sqrt {3} -1}\ [6pt]
&=\ drac {\ sqrt {3} +1} {\ sqrt {3} -1}
\ mwisho {align*}\]
Kupata thamani halisi ya\(\tan\left (\dfrac{2\pi}{3}+\dfrac{\pi}{4}\right )\).
- Jibu
-
\(\dfrac{1-\sqrt{3}}{1+\sqrt{3}}\)
Kutokana\(\sin \alpha=\frac{3}{5}, \quad 0<\alpha<\frac{\pi}{2},\) na\(\cos \beta=−\frac{5}{13}, \quad \pi<\beta<\frac{3\pi}{2}\),
pata
- \(\sin(\alpha+\beta)\)
- \(\cos(\alpha+\beta)\)
- \(\tan(\alpha+\beta)\)
- \(\tan(\alpha−\beta)\)
Suluhisho
Tunaweza kutumia jumla na tofauti formula kutambua jumla au tofauti ya pembe wakati uwiano wa sine, cosine, au tangent hutolewa kwa kila pembe ya mtu binafsi. Kwa kufanya hivyo, sisi kujenga kile kinachoitwa pembetatu rejea kusaidia kupata kila sehemu ya jumla na tofauti formula.
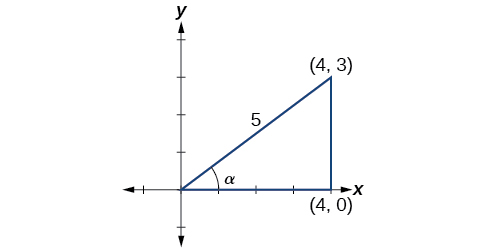
- Ili kupata\(\sin(\alpha+\beta)\), tunaanza\(\sin \alpha=\dfrac{3}{5}\) na\(0<\alpha<\dfrac{\pi}{2}\). Upande wa kinyume\(\alpha\) una urefu wa 3, hypotenuse ina urefu wa 5, na\(\alpha\) iko katika quadrant ya kwanza. Angalia Kielelezo\(\PageIndex{4}\). Kutumia Theorem ya Pythagorean, tunaweza kupata urefu wa upande\(a\):
\[\begin{align*} a^2+3^2&= 5^2\\[4pt] a^2&= 16\\[4pt] a&= 4 \end{align*}\]
Tangu\(\cos \beta=−\dfrac{5}{13}\) na\(\pi<\beta<\dfrac{3\pi}{2}\), upande wa karibu na\(\beta\) ni\(−5\), hypotenuse ni\(13\), na\(\beta\) iko katika quadrant ya tatu. Angalia Kielelezo\(\PageIndex{5}\). Tena, kwa kutumia Theorem ya Pythagorean, tuna
\[\begin{align*} {(-5)}^2+a^2&= {13}^2\\[4pt] 25+a^2&= 169\\[4pt] a^2&= 144\\[4pt] a&= \pm 12 \end{align*}\]
Tangu\(\beta\) ni katika roboduara ya tatu,\(a=–12\).
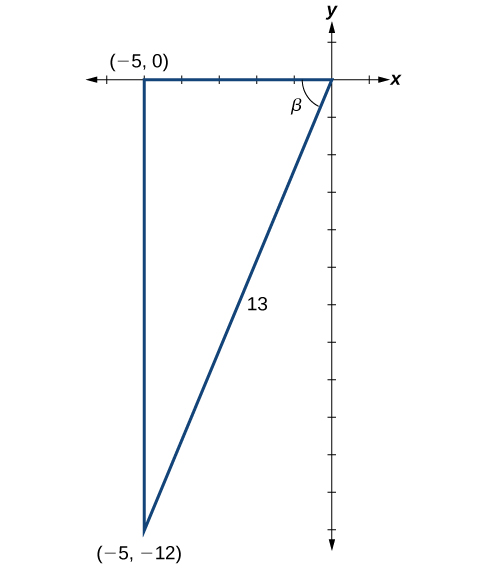
Hatua inayofuata ni kutafuta cosine ya\(\alpha\) na sine ya\(\beta\). Cosine ya α α ni upande wa karibu juu ya hypotenuse. Tunaweza kuipata kutoka pembetatu katika Kielelezo\(\PageIndex{5}\):\(\cos \alpha=\dfrac{4}{5}\). Tunaweza pia kupata sine ya\(\beta\) kutoka pembetatu katika Kielelezo\(\PageIndex{5}\), kama upande kinyume juu ya hypotenuse:\(\sin \beta=−\dfrac{12}{13}\). Sasa tuko tayari kutathmini\(\sin(\alpha+\beta)\).
\[\begin{align*} \sin(\alpha+\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \left(\dfrac{3}{5}\right)\left(-\dfrac{5}{13}\right )+\left (\dfrac{4}{5}\right )\left(-\dfrac{12}{13}\right )\\[4pt] &= -\dfrac{15}{65}-\dfrac{48}{65}\\[4pt] &= -\dfrac{63}{65} \end{align*}\]
- Tunaweza kupata kwa\(\cos(\alpha+\beta)\) namna hiyo. Sisi badala ya maadili kulingana na formula.
\[\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta-\sin \alpha \sin \beta\\[4pt] &= \left(\dfrac{4}{5}\right)\left(-\dfrac{5}{13}\right)-\left(\dfrac{3}{5}\right )\left(-\dfrac{12}{13}\right)\\[4pt] &= -\dfrac{20}{65}+\dfrac{36}{65}\\[4pt] &= \dfrac{16}{65} \end{align*}\]
- Kwa\(\tan(\alpha+\beta)\), ikiwa\(\sin \alpha=\dfrac{3}{5}\) na\(\cos \alpha=\dfrac{4}{5}\), basi
\(\tan \alpha=\dfrac{\dfrac{3}{5}}{\dfrac{4}{5}}=\dfrac{3}{4}\)
Kama\(\sin \beta=−\dfrac{12}{13}\) na\(\cos \beta=−\dfrac{5}{13}\), basi
\(\tan \beta=\dfrac{−\dfrac{12}{13}}{−\dfrac{5}{13}}=\dfrac{12}{5}\)
Kisha,
\ [kuanza {align*}
\ tan (\ alpha+\ beta) &=\ dfrac {\ tan\ alpha+\ tan\ beta} {1-\ tan\ alpha\ tan\ beta}\\ [6pt]
&=\ dfrac {3} {4} +\ dfrac {12} {5}} {1-\ dfrac {3} 4}\ kushoto (\ dfrac {12} {5}\ haki)}\\ [6pt]
&=\ dfrac {\ dfrac {63} {20}} {-\ dfrac {16} {20}}\\ [6pt]
& amp; = -\ dfrac {63} {16}
\ mwisho {align*}\]
- Ili kupata\(\tan(\alpha−\beta)\), tuna maadili tunayohitaji. Tunaweza badala yao katika na kutathmini.
\ [kuanza {align*}
\ tan (\ alpha-\ beta) &=\ dfrac {\ tan\ alpha-\ tan\ beta} {1+\ tan\ alpha\ tan\ beta}\\ [6pt]
&=\ dfrac {3} {4} -\ dfrac {4}\ kushoto (\ dfrac {12} {5}\ haki)}\\ [6pt]
&=\ dfrac {-\ dfrac {33} {20}} {\ dfrac {56} {20}}\\ [6pt]
& amp; = -\ dfrac {33} {56}
\ mwisho {align*}\]
Uchambuzi
Hitilafu ya kawaida wakati wa kushughulikia matatizo kama haya ni kwamba tunaweza kujaribiwa kufikiri hiyo\(\alpha\) na\(\beta\) ni pembe katika pembetatu moja, ambayo bila shaka, sio. Pia kumbuka kuwa
\(\tan(\alpha+\beta)=\sin(\alpha+\beta)\cos(\alpha+\beta)\)
Kutumia Fomu za Jumla na Tofauti kwa Cofunctions
Sasa kwa kuwa tunaweza kupata sine, cosine, na kazi tangent kwa kiasi na tofauti ya pembe, tunaweza kutumia yao kufanya hivyo kwa cofunctions yao. Unaweza kukumbuka kutoka Right Triangle Trigonometry kwamba, kama jumla ya pembe mbili chanya ni\(\frac{\pi}{2}\), wale pembe mbili ni mchango, na jumla ya pembe mbili papo hapo katika pembetatu haki ni\(\frac{\pi}{2}\), hivyo wao pia ni mchango. Katika Kielelezo\(\PageIndex{6}\), taarifa kwamba kama moja ya pembe papo hapo ni kinachoitwa kama\(\theta\), basi angle nyingine papo hapo lazima lebo\(\frac{\pi}{2}−\theta\).
Angalia pia kwamba\(\sin \theta=\cos\left(\frac{\pi}{2}−\theta\right)\), ambayo ni kinyume juu ya hypotenuse. Hivyo, wakati pembe mbili ni complimentary, tunaweza kusema kwamba sine ya\(\theta\) sawa na cofunction ya inayosaidia ya\(\theta\). Vile vile, tangent na cotangent ni cofunctions, na secant na cosecant ni cofunctions.
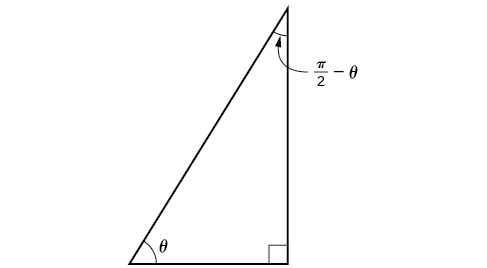
Kutoka kwa mahusiano haya, utambulisho wa cofunction huundwa. Kumbuka kwamba wewe kwanza ulikutana na utambulisho huu katika Mzunguko wa Unit: Kazi za Sine na Cosine.
Utambulisho wa cofunction ni muhtasari katika Jedwali\(\PageIndex{2}\).
| \(\sin \theta=\cos\left(\dfrac{\pi}{2}−\theta\right)\) | \(\cos \theta=\sin\left(\dfrac{\pi}{2}−\theta\right)\) |
| \(\tan \theta=\cot\left(\dfrac{\pi}{2}−\theta\right)\) | \(\cot \theta=\tan\left(\dfrac{\pi}{2}−\theta\right )\) |
| \(\sec \theta=\csc\left (\dfrac{\pi}{2}−\theta\right )\) | \(\csc \theta=\sec\left (\dfrac{\pi}{2}−\theta\right )\) |
Angalia kwamba formula katika meza pia inaweza kuhesabiwa haki kwa kutumia jumla na tofauti formula. Kwa mfano, kwa kutumia
\(\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\)
Tunaweza kuandika
\[\begin{align*} \cos\left (\dfrac{\pi}{2}-\theta \right )&= \cos \dfrac{\pi}{2} \cos \theta+\sin \dfrac{\pi}{2} \sin \theta \\[4pt] &=(0)\cos \theta+(1)\sin \theta \\[4pt] &=\sin \theta \end{align*}\]
Andika\(\tan \dfrac{\pi}{9}\) kwa suala la ushirikiano wake.
Suluhisho
Kazi ya\(\tan \theta=\cot\left (\dfrac{\pi}{2}−\theta\right )\). Hivyo,
\[\begin{align*} \tan\left (\dfrac{\pi}{9}\right )&= \cot\left (\dfrac{\pi}{2}-\dfrac{\pi}{9}\right )\\[4pt] &= \cot\left (\dfrac{9\pi}{18}-\dfrac{2\pi}{18}\right )\\[4pt] &= \cot\left (\dfrac{7\pi}{18}\right ) \end{align*}\]
Andika\(\sin \dfrac{\pi}{7}\) in terms of its cofunction.
- Jibu
-
\(\cos\left (\dfrac{5\pi}{14}\right )\)
Kutumia Fomu za Jumla na Tofauti ili kuthibitisha Utambulisho
Kuthibitisha utambulisho ina maana ya kuonyesha kwamba equation inashikilia maadili yote ya kutofautiana. Inasaidia kuwa ukoo sana na utambulisho au kuwa na orodha yao kupatikana wakati wa kufanya kazi matatizo. Kupitia sheria za jumla zilizowasilishwa mapema zinaweza kusaidia kurahisisha mchakato wa kuthibitisha utambulisho.
- Anza na maneno upande wa ishara sawa inayoonekana ngumu zaidi. Andika upya maneno hayo mpaka yanafanana na upande mwingine wa ishara sawa. Mara kwa mara, tunaweza kuwa na mabadiliko ya pande zote mbili, lakini kufanya kazi kwa upande mmoja tu ni ufanisi zaidi.
- Angalia fursa za kutumia jumla na tofauti formula.
- Andika upya kiasi au tofauti za quotients kama quotients moja.
- Ikiwa mchakato unakuwa mbaya, fungua upya maneno kwa suala la sines na cosines.
Thibitisha utambulisho\(\sin(\alpha+\beta)+\sin(\alpha−\beta)=2\sin \alpha \cos \beta\).
Suluhisho
Tunaona kwamba upande wa kushoto wa equation ni pamoja na sines ya jumla na tofauti ya pembe.
\(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\)
\(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\)
Tunaweza kuandika upya kila kutumia jumla na tofauti formula.
\[\begin{align*} \sin(\alpha+\beta)+\sin(\alpha-\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta+\sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] &= 2\sin \alpha \cos \beta \end{align*}\]
Tunaona kwamba utambulisho umehakikishiwa.
Thibitisha utambulisho uliofuata.
\(\dfrac{\sin(\alpha−\beta)}{\cos \alpha \cos \beta}=\tan \alpha−\tan \beta\)
Suluhisho
Tunaweza kuanza kwa kuandika upya namba upande wa kushoto wa equation.
\[\begin{align*} \dfrac{\sin(\alpha-\beta)}{\cos \alpha \cos \beta}&= \dfrac{\sin \alpha \cos \beta-\cos \alpha \sin \beta}{\cos \alpha \cos \beta}\\[4pt] &= \dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}-\dfrac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta} & & \text{Rewrite using a common denominator}\\[4pt] &= \dfrac{\sin \alpha}{\cos \alpha}-\dfrac{\sin \beta}{\cos \beta} & & \text{Cancel}\\[4pt] &= \tan \alpha-\tan \beta & & \text{Rewrite in terms of tangent} \end{align*}\]
Thibitisha utambulisho:\(\tan(\pi−\theta)=−\tan \theta\).
- Jibu
-
\[\begin{align*} \tan(\pi-\theta)&= \dfrac{\tan(\pi)-\tan \theta}{1+\tan(\pi)\tan \theta}\\[4pt] &= \dfrac{0-\tan \theta}{1+0\cdot \tan \theta}\\[4pt] &= -\tan \theta \end{align*}\]
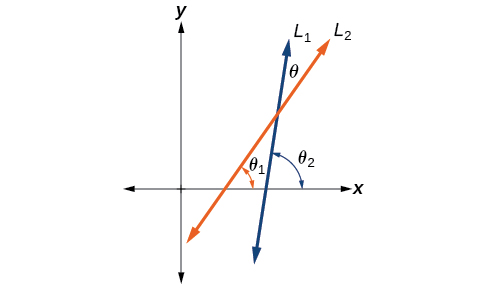
Hebu\(L_1\) na\(L_2\) ueleze mistari miwili isiyo ya wima inayoingiliana, na hebu\(θ\) ueleze angle ya papo hapo kati\(L_1\) na\(L_2\). Angalia Kielelezo\(\PageIndex{7}\). Onyesha kwamba
\(\tan \theta=\dfrac{m_2-m_1}{1+m_1m_2}\)
wapi\(m_1\) na\(m_2\) ni mteremko wa\(L_1\) na\(L_2\) kwa mtiririko huo. (kidokezo: Matumizi ya ukweli kwamba\(\tan \theta_1=m_1\) na\(\tan \theta_2=m_2\).)
Suluhisho
Kutumia formula tofauti kwa tangent, tatizo hili halionekani kuwa ngumu kama inaweza.
\[\begin{align*} \tan \theta&= \tan(\theta_2-\theta_1)\\[4pt] &= \dfrac{\tan \theta_2-\tan \theta_1}{1+\tan \theta_1 \tan \theta_2}\\[4pt] &= \dfrac{m_2-m_1}{1+m_1m_2} \end{align*}\]
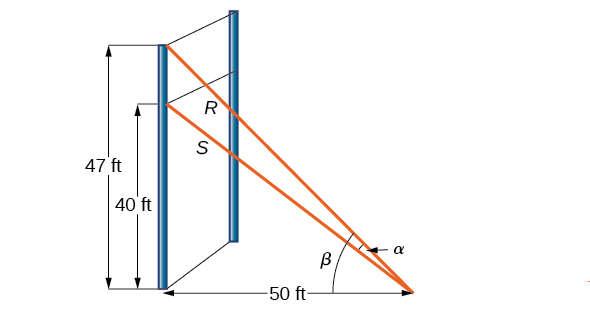
Kwa ukuta wa kupanda, waya wa mvulana\(R\) huunganishwa\(47\) miguu juu ya pole ya wima. Aliongeza msaada hutolewa na mwingine guy-waya\(S\) masharti\(40\) miguu juu ya ardhi juu ya pole moja. Ikiwa waya zinaunganishwa na\(50\) miguu ya chini kutoka kwenye pigo, pata angle\(\alpha\) kati ya waya. Angalia Kielelezo\(\PageIndex{8}\).
Suluhisho
Hebu kwanza tufanye muhtasari habari tunayoweza kukusanya kutoka kwenye mchoro. Kama tu pande zilizo karibu na angle ya kulia zinajulikana, tunaweza kutumia kazi ya tangent. Kumbuka kwamba\(\tan \beta=\frac{47}{50}\), na\(\tan(\beta−\alpha)=\frac{40}{50}=\frac{4}{5}\). Basi tunaweza kutumia tofauti formula kwa tangent.
\[\tan(\beta-\alpha) = \dfrac{\tan \beta-\tan \alpha}{1+\tan \beta \tan \alpha}\]
Sasa, badala ya maadili tunayoyajua katika formula, tuna,
\ [kuanza {align*}\ dfrac {4} {5} &=\ dfrac {\ tfrac {47} {50} -\ tan\ alpha} {1+\ tfrac {47} {50}\ tan\ alpha}\ [4pt]
4\ kushoto (1+\ tfrac {47} 50}\ tan\ alpha\ haki) &= 5\ kushoto (\ tfrac {47} {50} -\ tan\ alpha\ haki)\ mwisho {align*}\]
Tumia mali ya kusambaza, na kisha kurahisisha kazi.
\ [kuanza {align*} 4 (1) +4\ kushoto (\ tfrac {47} {50}\ haki)\ tan\ alpha &= 5\ kushoto (\ tfrac {47} {50}\ haki) -5\ tan\ alpha\\ [4pt]
4+3.76\ tan\ alpha&= 4.7-5\ tan\ alpha\\ [4pt]
5\ tan\ alpha\ +3.76\ tan\ alpha&= 0.7\\ [4pt]
8.76\ tan\ alpha&= 0.7\\ [4pt]
\ tan\ alpha&\ takriban 0.07991\\ [4pt]
\ tan^ {-1} (0.07991) &\ takriban .079741\ mwisho {align*}\]
Sasa tunaweza kuhesabu angle kwa digrii.
\ [kuanza {align*}\ alpha &\ takriban 0.079741\ kushoto (\ dfrac {180} {\ pi}\ haki)\\ [4pt]
&\ takriban 4.57^ {\ circ}
\ mwisho {align*}\]
Uchambuzi
Mara kwa mara, wakati programu inaonekana ambayo inajumuisha pembetatu sahihi, tunaweza kufikiri kwamba kutatua ni suala la kutumia Theorem ya Pythagorean. Hiyo inaweza kuwa sehemu ya kweli, lakini inategemea kile tatizo linauliza na ni habari gani inayotolewa.
Fikia rasilimali hizi mtandaoni kwa maelekezo ya ziada na mazoezi na utambulisho wa jumla na tofauti.
- Utambulisho wa Jumla na Tofauti kwa Cosine
- Jumla na Tofauti Utambulisho kwa Sine
- Utambulisho wa Jumla na Tofauti kwa Tangent
Mlinganyo muhimu
| Mfumo wa jumla wa Cosine | \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\) |
| Mfumo wa Tofauti kwa Cosine | \(\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
| Mfumo wa jumla kwa ajili ya Sine | \(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\) |
| Tofauti formula kwa ajili ya Sine | \(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\) |
| Mfumo wa jumla kwa Tangent | \(\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\) |
| Tofauti formula kwa Tangent | \(\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
| Utambulisho wa ushirikiano |
\(\sin \theta=\cos\left(\dfrac{\pi}{2}-\theta\right)\) \(\cos \theta=\sin\left(\dfrac{\pi}{2}-\theta\right)\) \(\tan \theta=\cot\left(\dfrac{\pi}{2}-\theta\right)\) \(\cot \theta=\tan\left(\dfrac{\pi}{2}-\theta\right)\) \(\sec \theta=\csc\left(\dfrac{\pi}{2}-\theta\right)\) \(\csc \theta=\sec\left(\dfrac{\pi}{2}-\theta\right)\) |
Dhana muhimu
- Fomu ya jumla ya cosines inasema kwamba cosine ya jumla ya pembe mbili ni sawa na bidhaa ya cosines ya pembe bala bidhaa ya sines ya pembe. Fomu tofauti ya cosines inasema kwamba cosine ya tofauti ya pembe mbili ni sawa na bidhaa ya cosines ya pembe pamoja na bidhaa ya sines ya pembe.
- Fomu za jumla na tofauti zinaweza kutumika kupata maadili halisi ya sine, cosine, au tangent ya angle. Angalia Mfano\(\PageIndex{1}\) na Mfano\(\PageIndex{2}\).
- Fomu ya jumla ya sines inasema kwamba sine ya jumla ya pembe mbili ni sawa na bidhaa ya sine ya angle ya kwanza na cosine ya angle ya pili pamoja na bidhaa ya cosine ya angle ya kwanza na sine ya angle ya pili. Fomu tofauti ya sines inasema kwamba sine ya tofauti ya pembe mbili ni sawa na bidhaa ya sine ya angle ya kwanza na cosine ya angle ya pili bala bidhaa ya cosine ya angle ya kwanza na sine ya angle ya pili. Angalia Mfano\(\PageIndex{3}\).
- Jumla na tofauti formula kwa sine na cosine pia inaweza kutumika kwa kazi inverse trigonometric. Angalia Mfano\(\PageIndex{4}\).
- Fomu ya jumla ya tangent inasema kwamba tangent ya jumla ya pembe mbili ni sawa na jumla ya tangents ya pembe zilizogawanywa na\(1\) kupunguza bidhaa ya tangents ya pembe. Fomu tofauti ya tangent inasema kwamba tangent ya tofauti ya pembe mbili ni sawa na tofauti ya tangents ya pembe zilizogawanywa na\(1\) pamoja na bidhaa ya tangents ya pembe. Angalia Mfano\(\PageIndex{5}\).
- Theorem ya Pythagorean pamoja na jumla na tofauti formula inaweza kutumika kupata kiasi nyingi na tofauti ya pembe. Angalia Mfano\(\PageIndex{6}\).
- Utambulisho wa cofunction hutumika kwa pembe za ziada na jozi za kazi za usawa. Angalia Mfano\(\PageIndex{7}\).
- Sum na tofauti formula ni muhimu katika kuthibitisha utambulisho. Angalia Mfano\(\PageIndex{8}\) na Mfano\(\PageIndex{9}\).
- Matatizo ya maombi mara nyingi ni rahisi kutatua kwa kutumia jumla na tofauti formula. Angalia Mfano\(\PageIndex{10}\) na Mfano\(\PageIndex{11}\).


