7.1: Kutatua Ulinganisho wa Trigonometric na Utambulisho

Malengo ya kujifunza

• Thibitisha utambulisho wa msingi wa trigonometric.
• Kurahisisha maneno trigonometric kutumia algebra na utambulisho.

Katika sinema za upelelezi, tunaona wapelelezi wa kimataifa wenye pasipoti nyingi, kila mmoja akidai utambulisho tofauti. Hata hivyo, tunajua kwamba kila moja ya pasipoti hizo inawakilisha mtu huyo huyo. Utambulisho wa trigonometric hufanya kwa namna sawa na pasipoti nyingi—kuna njia nyingi za kuwakilisha usemi huo wa trigonometric. Kama vile kupeleleza kuchagua Italia pasipoti wakati wa kusafiri kwenda Italia, sisi kuchagua utambulisho ambayo inatumika kwa mazingira fulani wakati wa kutatua equation trigonometric.

Kielelezo\(\PageIndex{1}\): Pasi za kimataifa na nyaraka za kusafiri

Katika sehemu hii, tutaanza uchunguzi wa utambulisho wa msingi wa trigonometric, ikiwa ni pamoja na jinsi tunavyoweza kuthibitisha na jinsi tunavyoweza kuitumia ili kurahisisha maneno ya trigonometric.

Kuthibitisha Utambulisho wa Msingi wa Trigonometri

Utambulisho hutuwezesha kurahisisha maneno ngumu. Wao ni zana za msingi za trigonometry zinazotumiwa katika kutatua equations trigonometric, kama vile factoring, kutafuta denominators ya kawaida, na kutumia formula maalum ni zana za msingi za kutatua equations algebraic. Kwa kweli, tunatumia mbinu za algebraic daima ili kurahisisha maneno ya trigonometric. Mali ya msingi na formula za algebra, kama tofauti ya formula ya mraba na formula kamili ya mraba, itapunguza kazi inayohusika na maneno ya trigonometric na equations. Tayari tunajua kwamba kazi zote za trigonometric zinahusiana kwa sababu zote zinaelezwa kwa suala la mduara wa kitengo. Kwa hiyo, utambulisho wowote wa trigonometric unaweza kuandikwa kwa njia nyingi.

Ili kuthibitisha utambulisho wa trigonometric, kwa kawaida huanza na upande mgumu zaidi wa equation na kimsingi kuandika tena usemi mpaka umebadilishwa kuwa kujieleza sawa na upande mwingine wa equation. Wakati mwingine tunapaswa kuzingatia maneno, kupanua maneno, kupata denominators ya kawaida, au kutumia mikakati mingine ya algebraic ili kupata matokeo yaliyohitajika. Katika sehemu hii ya kwanza, tutafanya kazi na utambulisho wa msingi: utambulisho wa Pythagorean, utambulisho hata usio wa kawaida, utambulisho wa usawa, na utambulisho wa quotient.

Tutaanza na utambulisho wa Pythagorean (Jedwali\(\PageIndex{1}\)), ambazo ni equations zinazohusisha kazi za trigonometric kulingana na mali ya pembetatu sahihi. Tayari tumeona na kutumika kwanza ya hizi kubainisha, lakini sasa sisi pia kutumia utambulisho wa ziada.

Jedwali\(\PageIndex{1}\): Utambulisho wa Pythagorean

\({\sin}^2 \theta+{\cos}^2 \theta=1\)

\(1+{\cot}^2 \theta={\csc}^2 \theta\)

\(1+{\tan}^2 \theta={\sec}^2 \theta\)

Utambulisho wa pili na wa tatu unaweza kupatikana kwa kuendesha kwanza. Utambulisho\(1+{\cot}^2 \theta={\csc}^2 \theta\) hupatikana kwa kuandika upya upande wa kushoto wa equation kwa suala la sine na cosine.

Thibitisha:\(1+{\cot}^2 \theta={\csc}^2 \theta\)

\[\begin{align*} 1+{\cot}^2 \theta&= (1+\dfrac{{\cos}^2}{{\sin}^2})\qquad \text{Rewrite the left side}\\ &= \left(\dfrac{{\sin}^2}{{\sin}^2}\right)+\left (\dfrac{{\cos}^2}{{\sin}^2}\right)\qquad \text{Write both terms with the common denominator}\\ &= \dfrac{{\sin}^2+{\cos}^2}{{\sin}^2}\\ &= \dfrac{1}{{\sin}^2}\\ &= {\csc}^2 \end{align*}\]

Vile vile,\(1+{\tan}^2 \theta={\sec}^2 \theta\) inaweza kupatikana kwa kuandika upya upande wa kushoto wa utambulisho huu kwa suala la sine na cosine. Hii inatoa

\[\begin{align*} 1+{\tan}^2 \theta&= 1+{\left(\dfrac{\sin \theta}{\cos \theta}\right )}^2\qquad \text{Rewrite left side}\\ &= {\left (\dfrac{\cos \theta}{\cos \theta}\right )}^2+{\left (\dfrac{\sin \theta}{\cos \theta}\right)}^2\qquad \text{Write both terms with the common denominator}\\ &= \dfrac{{\cos}^2 \theta+{\sin}^2 \theta}{{\cos}^2 \theta}\\ &= \dfrac{1}{{\cos}^2 \theta}\\ &= {\sec}^2 \theta \end{align*}\]

Kumbuka kwamba tuliamua kazi gani za trigonometric ni isiyo ya kawaida na ambayo ni hata. Seti inayofuata ya utambulisho wa msingi ni seti ya utambulisho hata usio wa kawaida. Utambulisho hata usio wa kawaida unahusisha thamani ya kazi ya trigonometric kwa pembe iliyotolewa kwa thamani ya kazi kwa pembe tofauti (Jedwali\(\PageIndex{2}\)).

Jedwali\(\PageIndex{2}\): Hata-Odd Utambulisho

\(\tan(−\theta)=−\tan \theta\)	\(\sin(−\theta)=−\sin \theta\)	\(\cos(−\theta)=\cos \theta\)
\(\cot(−\theta)=−\cot \theta\)	\(\csc(−\theta)=−\csc \theta\)	\(\sec(−\theta)=\sec \theta\)

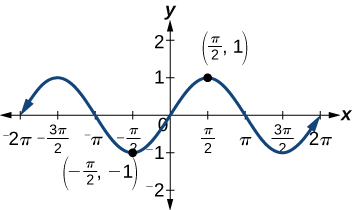
Kumbuka kwamba kazi isiyo ya kawaida ni moja ambayo\(f(−x)= −f(x)\) kwa ajili ya wote\(x\) katika uwanja off. f. kazi sine ni kazi isiyo ya kawaida kwa sababu\(\sin(−\theta)=−\sin \theta\). Grafu ya kazi isiyo ya kawaida ni sawa na asili. Kwa mfano, fikiria pembejeo zinazofanana za\(\dfrac{\pi}{2}\) na\(−\dfrac{\pi}{2}\). Pato la\(\sin\left (\dfrac{\pi}{2}\right )\) ni kinyume na pato la\(\sin \left (−\dfrac{\pi}{2}\right )\). Hivyo,

\[\begin{align*} \sin\left (\dfrac{\pi}{2}\right)&=1 \\[4pt] \sin\left (-\dfrac{\pi}{2}\right) &=-\sin\left (\dfrac{\pi}{2}\right) \\[4pt] &=-1 \end{align*}\]

Hii inavyoonekana katika Kielelezo\(\PageIndex{2}\).

Kielelezo\(\PageIndex{2}\): Grafu ya\(y=\sin \theta\)

Kumbuka kwamba hata kazi ni moja ambayo

\(f(−x)=f(x)\)kwa wote\(x\) katika uwanja wa\(f\)

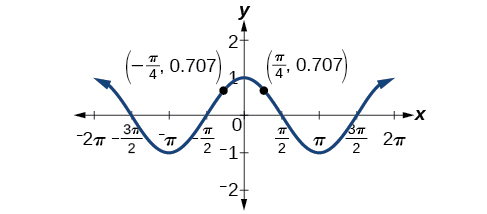
Grafu ya kazi hata ni sawa na y- axis. Kazi ya cosine ni kazi hata kwa sababu\(\cos(−\theta)=\cos \theta\). Kwa mfano, fikiria pembejeo zinazofanana\(\dfrac{\pi}{4}\) na\(−\dfrac{\pi}{4}\). Pato la\(\cos\left (\dfrac{\pi}{4}\right)\) ni sawa na pato la\(\cos\left (−\dfrac{\pi}{4}\right)\). Hivyo,

\[\begin{align*} \cos\left (−\dfrac{\pi}{4}\right ) &=\cos\left (\dfrac{\pi}{4}\right) \\[4pt] &≈0.707 \end{align*}\]

Angalia Kielelezo\(\PageIndex{3}\).

Kielelezo\(\PageIndex{3}\): Grafu ya\(y=\cos \theta\)

Kwa wote\(\theta\) katika uwanja wa kazi za sine na cosine, kwa mtiririko huo, tunaweza kusema yafuatayo:

• tangu\(\sin(−\theta)=−\sin \theta\), sine ni kazi isiyo ya kawaida.
• Tangu\(\cos(−\theta)=\cos \theta\), cosine ni kazi hata.

nyingine hata-isiyo ya kawaida utambulisho kufuata kutoka hata na isiyo ya kawaida asili ya kazi sine na cosine. Kwa mfano, fikiria utambulisho wa tangent,\(\tan(−\theta)=−\tan \theta\). Tunaweza kutafsiri tangent ya angle hasi kama

\[\tan (−\theta)=\dfrac{\sin (−\theta)}{\cos (−\theta)}=\dfrac{−\sin \theta}{\cos \theta}=−\tan \theta. \nonumber\]

Tangent hiyo ni kazi isiyo ya kawaida, ambayo ina maana kwamba\(\tan(−\theta)=−\tan(\theta)\) kwa wote\(\theta\) katika uwanja wa kazi tangent.

Utambulisho wa cotangent\(\cot(−\theta)=−\cot \theta\), pia hufuata kutoka kwa utambulisho wa sine na cosine. Tunaweza kutafsiri cotangent ya angle hasi kama

\[\cot(−\theta)=\dfrac{\cos(−\theta)}{\sin(−\theta)}=\dfrac{\cos \theta}{−\sin \theta}=−\cot \theta.\nonumber\]

Cotangent hiyo ni kazi isiyo ya kawaida, ambayo ina maana kwamba\(\cot(−\theta)=−\cot(\theta)\) kwa wote\(\theta\) katika uwanja wa kazi cotangent.

Kazi ya cosecant ni usawa wa kazi ya sine, ambayo ina maana kwamba cosecant ya angle hasi itafsiriwa kama

\[\csc(−\theta)=\dfrac{1}{\sin(−\theta)}=\dfrac{1}{−\sin \theta}=−\csc \theta. \nonumber\]

Kazi ya cosecant hiyo ni isiyo ya kawaida.

Hatimaye, kazi ya salama ni ya usawa wa kazi ya cosine, na secant ya angle hasi hutafsiriwa kama

\[\sec(−\theta)=\dfrac{1}{\cos(−\theta)}=\dfrac{1}{\cos \theta}=\sec \theta. \nonumber\]

Kazi ya secant ni hivyo hata.

Kwa jumla, kazi mbili tu za trigonometric, cosine na secant, ni hata. Kazi nyingine nne ni isiyo ya kawaida, kuthibitisha utambulisho hata-isiyo ya kawaida.

Seti inayofuata ya utambulisho wa msingi ni seti ya utambulisho wa usawa, ambao, kama jina lao linamaanisha, zinahusiana na kazi za trigonometric ambazo zinafaa kwa kila mmoja. (Jedwali\(\PageIndex{3}\)). Kumbuka kwamba sisi kwanza tulikutana na utambulisho huu wakati wa kufafanua kazi za trigonometric kutoka pembe za kulia katika Trigonometry ya Angle ya kulia.

Jedwali\(\PageIndex{3}\): Utambulisho wa Kukubaliana

\(\sin \theta=\dfrac{1}{\csc \theta}\)	\(\csc \theta=\dfrac{1}{\sin \theta}\)
\(\cos \theta = \dfrac{1}{\sec \theta}\)	\(\sec \theta=\dfrac{1}{\cos \theta}\)
\(\tan \theta=\dfrac{1}{\cot \theta}\)	\(\cot \theta=\dfrac{1}{\tan \theta}\)

Seti ya mwisho ya utambulisho ni seti ya utambulisho wa quotient, ambayo hufafanua uhusiano kati ya kazi fulani za trigonometric na inaweza kusaidia sana katika kuthibitisha utambulisho mwingine (Jedwali\(\PageIndex{4}\)).

Jedwali\(\PageIndex{4}\): Utambulisho wa Quotient

\(\tan \theta=\dfrac{\sin \theta}{\cos \theta}\)	\(\cot \theta=\dfrac{\cos \theta}{\sin \theta}\)

Utambulisho wa usawa na wa quotient unatokana na ufafanuzi wa kazi za msingi za trigonometric.

MUHTASARI WA UTAMBULISHO WA TRIGON

Utambulisho wa Pythagorean unategemea mali ya pembetatu sahihi.

\[{\cos}^2 \theta+{\sin}^2 \theta=1\]

\[1+{\cot}^2 \theta={\csc}^2 \theta\]

\[1+{\tan}^2 \theta={\sec}^2 \theta\]

Utambulisho hata usio wa kawaida unahusisha thamani ya kazi ya trigonometric kwa pembe iliyotolewa kwa thamani ya kazi kwa pembe tofauti.

\[\tan(−\theta)=−\tan \theta\]

\[\cot(−\theta)=−\cot \theta\]

\[\sin(−\theta)=−\sin \theta\]

\[\csc(−\theta)=−\csc \theta\]

\[\cos(−\theta)=\cos \theta\]

\[\sec(−\theta)=\sec \theta\]

Utambulisho wa usawa hufafanua usawa wa kazi za trigonometric.

\[\sin \theta=\dfrac{1}{\csc \theta}\]

\[\cos \theta=\dfrac{1}{\sec \theta}\]

\[\tan \theta=\dfrac{1}{\cot \theta}\]

\[\csc \theta=\dfrac{1}{\sin \theta}\]

\[\sec \theta=\dfrac{1}{\cos \theta}\]

\[\cot \theta=\dfrac{1}{\tan \theta}\]

Utambulisho wa quotient hufafanua uhusiano kati ya kazi za trigonometri.

\[\tan \theta=\dfrac{\sin \theta}{\cos \theta}\]

\[\cot \theta=\dfrac{\cos \theta}{\sin \theta}\]

Mfano\(\PageIndex{1}\): Graphing the Equations of an Identity

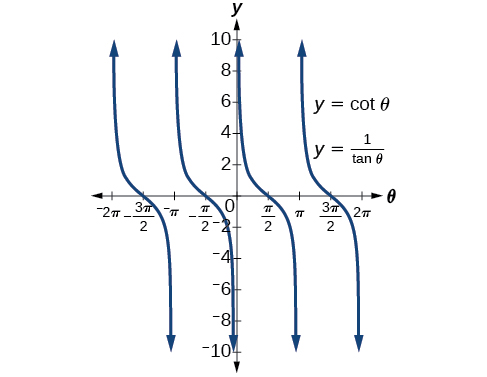
Grafu pande zote mbili za utambulisho\(\cot \theta=\dfrac{1}{\tan \theta}\). Kwa maneno mengine, kwenye calculator graphing, grafu\(y=\cot \theta\) na\(y=\dfrac{1}{\tan \theta}\).

Suluhisho

Angalia Kielelezo\(\PageIndex{4}\).

Kielelezo\(\PageIndex{4}\)

Uchambuzi

Tunaona grafu moja tu kwa sababu maneno yote yanazalisha picha sawa. Moja ni juu ya nyingine. Hii ni njia nzuri ya kuthibitisha utambulisho wowote. Ikiwa maneno yote yanatoa grafu sawa, basi lazima iwe utambulisho.

Jinsi ya: Kutokana na utambulisho wa trigonometric, hakikisha kuwa ni kweli.

1. Kazi upande mmoja wa equation. Kwa kawaida ni bora kuanza na upande mgumu zaidi, kwa kuwa ni rahisi kurahisisha kuliko kujenga.
2. Angalia fursa za kutafakari maneno, mraba binomial, au kuongeza sehemu ndogo.
3. Akibainisha kazi gani ziko katika kujieleza mwisho, tafuta fursa za kutumia utambulisho na ufanye mbadala sahihi.
4. Ikiwa hatua hizi hazipati matokeo yaliyohitajika, jaribu kubadili maneno yote kwa sines na cosines.

Mfano\(\PageIndex{2}\): Verifying a Trigonometric Identity

Thibitisha\(\tan \theta \cos \theta=\sin \theta\).

Suluhisho

Tutaanza upande wa kushoto, kwa kuwa ni upande mgumu zaidi:

\[ \begin{align*} \tan \theta \cos \theta &=\left(\dfrac{\sin \theta}{\cos \theta}\right)\cos \theta \\[4pt] &=\sin \theta \end{align*}\]

Uchambuzi

Utambulisho huu ulikuwa rahisi sana kuthibitisha, kama ilivyotakiwa tu kuandika\(\tan \theta\) kwa suala la\(\sin \theta\) na\(\cos \theta\).

Zoezi\(\PageIndex{1}\)

Thibitisha utambulisho\(\csc \theta \cos \theta \tan \theta=1\).

Jibu

\[ \begin{align*} \csc \theta \cos \theta \tan \theta=\left(\dfrac{1}{\sin \theta}\right)\cos \theta\left(\dfrac{\sin \theta}{\cos \theta}\right) \\[4pt] & =\dfrac{\cos \theta}{\sin \theta}(\dfrac{\sin \theta}{\cos \theta}) \\[4pt] & =\dfrac{\sin \theta \cos \theta}{\sin \theta \cos \theta} \\[4pt] &=1 \end{align*}\]

Mfano\(\PageIndex{3A}\): Verifying the Equivalency Using the Even-Odd Identities

Thibitisha ulinganifu ufuatao kwa kutumia utambulisho hata isiyo ya kawaida:

\((1+\sin x)[1+\sin(−x)]={\cos}^2 x\)

Suluhisho

Kufanya kazi upande wa kushoto wa equation, tuna

\( (1+\sin x)[1+\sin(−x)]=(1+\sin x)(1-\sin x)\)

Tangu

\[\begin{align*} \sin(-x)&= -\sin x \\ [5pt] &=1-{\sin}^2 x\qquad \text{Difference of squares} \\ [5pt] &={\cos}^2 x \\ {\cos}^2 x&= 1-{\sin}^2 x \\ \end{align*}\]

Mfano\(\PageIndex{3B}\): Verifying a Trigonometric Identity Involving \({\sec}^2 \theta\)

Thibitisha utambulisho\(\dfrac{{\sec}^2 \theta−1}{{\sec}^2 \theta}={\sin}^2 \theta\)

Suluhisho

Kama upande wa kushoto ni ngumu zaidi, hebu tuanze huko.

\ [kuanza {\ sec}
\ dfrac {\ sec} ^2\ theta-1} {\ sec} ^2\ theta} &=\ dfrac {({\ tan} ^2\ theta +1) -1} {\ sec} ^2\
theta}\\ {\ sec} ^2\ theta +1\\
&=\ dfrac {\ tan} ^2\ theta} {\ sec} ^2\ theta}\\
&= {\ tan} ^2\ theta\ kushoto (\ dfrac {1} {\ sec} ^2\ theta}\ haki)\\
&= {\ tan} ^2\ theta\ kushoto ({\ cos} ^2\ theta\ haki)\\
{\ cos} ^2\ theta&=\ dfrac {1} {\ sec} ^2\ theta}\\
&=\ kushoto (\ dfrac {\ dhambi} ^2\ theta} {\ sec} {\ sec} {\ theta} {\} ^2\ theta}\ haki)\\
{\ tan} ^2\ theta&=\ dfrac {\ dhambi} ^2\ theta} {\ cos} ^2\ theta} {\ cos} ^2\ theta }\\
&= {\ dhambi} ^2\ theta
\ mwisho {align*}\]

Kuna njia zaidi ya moja ya kuthibitisha utambulisho. Hapa kuna uwezekano mwingine. Tena, tunaweza kuanza na upande wa kushoto.

\[\begin{align*} \dfrac{{\sec}^2 \theta-1}{{\sec}^2 \theta}&= \dfrac{{\sec}^2 \theta}{{\sec}^2 \theta}-\dfrac{1}{{\sec}^2 \theta}\\ &= 1-{\cos}^2 \theta\\ &= {\sin}^2 \theta \end{align*}\]

Uchambuzi

Katika njia ya kwanza, tulitumia utambulisho\({\sec}^2 \theta={\tan}^2 \theta+1\) na kuendelea kurahisisha. Katika njia ya pili, tunagawanya sehemu, kuweka maneno yote kwa namba juu ya denominator ya kawaida. Tatizo hili linaonyesha kwamba kuna njia nyingi tunaweza kuthibitisha utambulisho. Kuajiri ubunifu fulani wakati mwingine kunaweza kurahisisha utaratibu. Kwa muda mrefu kama mbadala ni sahihi, jibu litakuwa sawa.

Zoezi\(\PageIndex{2}\)

Onyesha hilo\(\dfrac{\cot \theta}{\csc \theta}=\cos \theta\).

Jibu

\[\begin{align*} \dfrac{\cot \theta}{\csc \theta}&= \dfrac{\tfrac{\cos \theta}{\sin \theta}}{\dfrac{1}{\sin \theta}}\\ &= \dfrac{\cos \theta}{\sin \theta}\cdot \dfrac{\sin \theta}{1}\\ &= \cos \theta \end{align*}\]

Mfano\(\PageIndex{4}\): Creating and Verifying an Identity

Kujenga utambulisho kwa kujieleza\(2 \tan \theta \sec \theta\) kwa kuandika upya madhubuti katika suala la sine.

Suluhisho

Kuna njia kadhaa za kuanza, lakini hapa tutatumia utambulisho wa quotient na usawa ili kuandika tena maneno:

\[\begin{align*} 2 \tan \theta \sec \theta&= 2\left (\dfrac{\sin \theta}{\cos \theta}\right )\left(\dfrac{1}{\cos \theta}\right )\\ &= \dfrac{2\sin \theta}{{\cos}^2 \theta}\\ &= \dfrac{2\sin \theta}{1-{\sin}^2 \theta}\qquad \text{Substitute } 1-{\sin}^2 \theta \text{ for } {\cos}^2 \theta \end{align*}\]

Hivyo,

\(2 \tan \theta \sec \theta=\dfrac{2 \sin \theta}{1−{\sin}^2 \theta}\)

Mfano\(\PageIndex{5}\): Verifying an Identity Using Algebra and Even/Odd Identities

Thibitisha utambulisho:

\(\dfrac{{\sin}^2(−\theta)−{\cos}^2(−\theta)}{\sin(−\theta)−\cos(−\theta)}=\cos \theta−\sin \theta\)

Suluhisho

Hebu tuanze na upande wa kushoto na kurahisisha:

\[\begin{align*} \dfrac{{\sin}^2(-\theta)-{\cos}^2(-\theta)}{\sin(-\theta)-\cos(-\theta)}&= \dfrac{{[\sin(-\theta)]}^2-{[\cos(-\theta)]}^2}{\sin(-\theta)-\cos(-\theta)}\\ &= \dfrac{{(-\sin \theta)}^2-{(\cos \theta)}^2}{-\sin \theta -\cos \theta} \;\; \; , \sin(-x) = -\sin\space x\text { and } \cos(-x)=\cos \space x\\ &= \dfrac{{(\sin \theta)}^2-{(\cos \theta)}^2}{-\sin \theta -\cos \theta}\qquad \text{Difference of squares}\\ &= \dfrac{(\sin \theta-\cos \theta)(\sin \theta+\cos \theta)}{-(\sin \theta+\cos \theta)}\\ &= \cos \theta-\sin \theta \end{align*}\]

Zoezi\(\PageIndex{3}\)

Thibitisha utambulisho\(\dfrac{{\sin}^2 \theta−1}{\tan \theta \sin \theta−\tan \theta}=\dfrac{\sin \theta+1}{\tan \theta}\).

Jibu

\[\begin{align*} \dfrac{{\sin}^2 \theta-1}{\tan \theta \sin \theta-\tan \theta}&= \dfrac{(\sin \theta +1)(\sin \theta -1)}{\tan \theta(\sin \theta -1)}\\ &= \dfrac{\sin \theta+1}{\tan \theta} \end{align*}\]

Mfano\(\PageIndex{6}\): Verifying an Identity Involving Cosines and Cotangents

Thibitisha utambulisho:\((1−{\cos}^2 x)(1+{\cot}^2 x)=1\).

Suluhisho

\[\begin{align*} (1-{\cos}^2 x)(1+{\cot}^2 x)&= (1-{\cos}^2 x)\left(1+\dfrac{{\cos}^2 x}{{\sin}^2 x}\right)\\ &= (1-{\cos}^2 x)\left(\dfrac{{\sin}^2 x}{{\sin}^2 x}+\dfrac{{\cos}^2 x}{{\sin}^2 x}\right )\qquad \text{Find the common denominator}\\ &= (1-{\cos}^2 x)\left(\dfrac{{\sin}^2 x +{\cos}^2 x}{{\sin}^2 x}\right)\\ &= ({\sin}^2 x)\left (\dfrac{1}{{\sin}^2 x}\right )\\ &= 1 \end{align*}\]

Kutumia Algebra kurahisisha Maneno ya Trigonometric

Tumeona kwamba algebra ni muhimu sana katika kuthibitisha utambulisho wa trigonometric, lakini ni muhimu sana katika kurahisisha maneno ya trigonometric kabla ya kutatua. Kuwa ukoo na mali ya msingi na formula za algebra, kama vile tofauti ya formula ya mraba, formula kamili ya mraba, au badala, itapunguza kazi inayohusika na maneno ya trigonometric na equations.

Kwa mfano, equation\((\sin x+1)(\sin x−1)=0\) inafanana na equation\((x+1)(x−1)=0\), ambayo inatumia fomu factored ya tofauti ya mraba. Kutumia algebra hufanya kutafuta suluhisho moja kwa moja na ya kawaida. Tunaweza kuweka kila sababu sawa na sifuri na kutatua. Huu ni mfano mmoja wa kutambua mifumo ya algebraic katika maneno ya trigonometric au equations.

Mfano mwingine ni tofauti ya mraba formula,\(a^2−b^2=(a−b)(a+b)\), ambayo hutumika sana katika maeneo mengi zaidi ya hisabati, kama vile uhandisi, usanifu, na fizikia. Tunaweza pia kuunda utambulisho wetu wenyewe kwa kuendelea kupanua kujieleza na kufanya mbadala zinazofaa. Kutumia mali ya algebraic na formula hufanya equations nyingi za trigonometric rahisi kuelewa na kutatua.

Mfano\(\PageIndex{7A}\): Writing the Trigonometric Expression as an Algebraic Expression

Andika maneno yafuatayo ya trigonometric kama kujieleza kwa algebraic:\(2{\cos}^2 \theta+\cos \theta−1\).

Suluhisho

Kumbuka kwamba muundo kuonyeshwa ina fomu sawa na kujieleza kiwango quadratic,\(ax^2+bx+c\). Kuruhusu\(\cos \theta=x\), tunaweza kuandika upya maneno kama ifuatavyo:

\(2x^2+x−1\)

Maneno haya yanaweza kuhesabiwa kama\((2x+1)(x−1)\). Kama ni kuweka sawa na sifuri na tulitaka kutatua equation, tunataka kutumia sifuri sababu mali na kutatua kila sababu kwa\(x\). Katika hatua hii, tunataka kuchukua nafasi\(x\)\(\cos \theta\) na kutatua kwa\(\theta\).

Mfano\(\PageIndex{7B}\): Rewriting a Trigonometric Expression Using the Difference of Squares

Andika upya kujieleza kwa trigonometric kwa kutumia tofauti ya mraba:\(4{cos}^2 \theta−1\).

Suluhisho

Angalia kwamba mgawo wote na kujieleza kwa trigonometric katika muda wa kwanza ni mraba, na mraba wa namba 1 ni 1. Hii ni tofauti ya mraba.

\[\begin{align*} 4{\cos}^2 \theta-1&= {(2\cos \theta)}^2-1\\ &= (2\cos \theta-1)(2\cos \theta+1) \end{align*}\]

Uchambuzi

Kama maneno haya yaliandikwa katika mfumo wa equation kuweka sawa na sifuri, tunaweza kutatua kila sababu kwa kutumia sifuri sababu mali. Tunaweza pia kutumia badala kama tulivyofanya katika tatizo uliopita na basi\(\cos \theta=x\), kuandika upya kujieleza kama\(4x^2−1\), na sababu\((2x−1)(2x+1)\). Kisha kuchukua nafasi\(x\)\(\cos \theta\) na kutatua kwa angle.

Zoezi\(\PageIndex{4}\)

Andika upya kujieleza kwa trigonometric kwa kutumia tofauti ya mraba:\(25−9{\sin}^2 \theta\).

Jibu

Hii ni tofauti ya mraba formula:\(25−9{\sin}^2 \theta=(5−3\sin \theta)(5+3\sin \theta)\).

Mfano\(\PageIndex{8}\): Simplify by Rewriting and Using Substitution

Kurahisisha usemi kwa kuandika upya na kutumia utambulisho:

\({\csc}^2 \theta−{\cot}^2 \theta\)

Suluhisho

Tunaweza kuanza na utambulisho wa Pythagorean.

\[\begin{align*} 1+{\cot}^2 \theta&= {\csc}^2 \theta\\ \text{Now we can simplify by substituting } 1+{\cot}^2 \theta \text{ for } {\csc}^2 \theta\\ {\csc}^2 \theta-{\cot}^2 \theta&= 1+{\cot}^2 \theta-{\cot}^2 \theta\\ &= 1 \end{align*}\]

Zoezi\(\PageIndex{5}\)

Tumia mbinu za algebraic ili kuthibitisha utambulisho:\(\dfrac{\cos \theta}{1+\sin \theta}=\dfrac{1−\sin \theta}{\cos \theta}\).

(Kidokezo: Kuzidisha nambari na denominator upande wa kushoto na\(1−\sin \theta\).)

Jibu

\[\begin{align*} \dfrac{\cos \theta}{1+\sin \theta}\left(\dfrac{1-\sin \theta}{1-\sin \theta}\right)&= \dfrac{\cos \theta (1-\sin \theta)}{1-{\sin}^2 \theta}\\ &= \dfrac{\cos \theta (1-\sin \theta)}{{\cos}^2 \theta}\\ &= \dfrac{1-\sin \theta}{\cos \theta} \end{align*}\]

vyombo vya habari

Fikia rasilimali hizi mtandaoni kwa maelekezo ya ziada na mazoezi na utambulisho wa msingi wa trigonometric.

• Utambulisho wa msingi wa trigonometri
• Kuthibitisha Utambulisho wa Trigonometri

Mlinganyo muhimu

Utambulisho wa Pythagorean	\({\cos}^2 \theta+{\sin}^2 \theta=1\) \(1+{\cot}^2 \theta={\csc}^2 \theta\) \(1+{\tan}^2 \theta={\sec}^2 \theta\)
Hata-isiyo ya kawaida utambulisho	\(\tan(−\theta)=-\tan \theta\) \(\cot(-\theta)=-\cot \theta\) \(\sin(-\theta)=-\sin \theta\) \(\csc(-\theta)=-\csc \theta\) \(\cos(-\theta)=\cos \theta\) \(\sec(-\theta)=\sec \theta\)
Utambulisho wa kurudisha	\(\sin \theta=\dfrac{1}{\csc \theta}\) \(\cos \theta=\dfrac{1}{\sec \theta}\) \(\tan \theta=\dfrac{1}{\cot \theta}\) \(\csc \theta=\dfrac{1}{\sin \theta}\) \(\sec \theta=\dfrac{1}{\cos \theta}\) \(\cot \theta=\dfrac{1}{\tan \theta}\)
Utambulisho wa Quotient	\(\tan \theta=\dfrac{\sin \theta}{\cos \theta}\) \(\cot \theta=\dfrac{\cos \theta}{\sin \theta}\)

Dhana muhimu

• Kuna njia nyingi za kuwakilisha kujieleza kwa trigonometric. Kuthibitisha utambulisho unaonyesha jinsi maneno yanaweza kuandikwa upya ili kurahisisha tatizo.
• Graphing pande zote mbili za utambulisho kutathibitisha. Angalia Mfano\(\PageIndex{1}\).
• Kurahisisha upande mmoja wa equation kuwa sawa upande mwingine ni njia nyingine ya kuthibitisha utambulisho. Angalia Mfano\(\PageIndex{2}\) na Mfano\(\PageIndex{3}\).
• Njia ya kuthibitisha utambulisho inategemea asili ya utambulisho. Mara nyingi ni muhimu kuanza upande mgumu zaidi wa equation. Angalia Mfano\(\PageIndex{4}\).
• Tunaweza kuunda utambulisho na kisha uhakikishe. Angalia Mfano\(\PageIndex{5}\).
• Kuthibitisha utambulisho unaweza kuhusisha algebra na utambulisho wa msingi. Angalia Mfano\(\PageIndex{6}\) na Mfano\(\PageIndex{7}\).
• Mbinu za algebraic zinaweza kutumika kurahisisha maneno ya trigonometric. Tunatumia mbinu za algebraic katika maandishi haya, kwa kuwa zinajumuisha sheria za msingi za hisabati. Angalia Mfano\(\PageIndex{8}\), Mfano\(\PageIndex{9}\), na Mfano\(\PageIndex{10}\).