7.3: Mbili-Angle, Nusu-Angle, na Kupunguza Formula

Malengo ya kujifunza

• Tumia formula mbili za angle ili kupata maadili halisi
• Tumia fomu mbili za angle ili kuthibitisha utambulisho
• Tumia formula za kupunguza ili kurahisisha kujieleza
• Tumia formula za nusu-angle ili kupata maadili halisi

Ramps za baiskeli zilizofanywa kwa ushindani (angalia Mchoro\(\PageIndex{1}\)) zinapaswa kutofautiana kwa urefu kulingana na kiwango cha ujuzi wa washindani. Kwa washindani wa juu, angle iliyoundwa na barabara na ardhi inapaswa kuwa\(\theta\) hivyo\(\tan \theta=\dfrac{5}{3}\). Pembe imegawanywa kwa nusu kwa novices. Je, ni mwinuko wa barabara kwa novices? Katika sehemu hii, tutachunguza makundi matatu ya ziada ya utambulisho ambayo tunaweza kutumia ili kujibu maswali kama haya.

Kielelezo\(\PageIndex{1}\): Baiskeli ramps kwa wanunuzi juu na mwinuko elekea kuliko wale iliyoundwa kwa ajili ya novices.

Kutumia Formula mbili za Angle ili Kupata Maadili halisi

Katika sehemu iliyopita, tulitumia fomu za kuongeza na kuondoa kwa kazi za trigonometric. Sasa, tunaangalia mwingine fomu hizo. Fomu mbili za angle ni kesi maalum ya jumla ya formula, wapi\(\alpha=\beta\). Kupata formula mbili-angle kwa sine huanza na formula jumla,

\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]

Kama sisi basi\(\alpha=\beta=\theta\), basi tuna

\[\begin{align*} \sin(\theta+\theta)&= \sin \theta \cos \theta+\cos \theta \sin \theta\\[4pt] \sin(2\theta)&= 2\sin \theta \cos \theta \end{align*}\]

Kupata pembe mbili kwa cosine inatupa chaguzi tatu. Kwanza, kuanzia formula jumla,\(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\), na kuruhusu\(\alpha=\beta=\theta\), tuna

\[\begin{align*} \cos(\theta+\theta)&= \cos \theta \cos \theta-\sin \theta \sin \theta\\[4pt] \cos(2\theta)&= {\cos}^2 \theta - {\sin}^2 \theta \end{align*}\]

Kutumia mali ya Pythagorean, tunaweza kupanua formula hii mbili-angle kwa cosine na kupata tofauti mbili zaidi. Tofauti ya kwanza ni:

\[\begin{align*} \cos(2\theta)&= {\cos}^2 \theta - {\sin}^2 \theta \\[4pt] &= (1-{\sin}^2 \theta)-{\sin}^2 \theta \end{align*}\]

Tofauti ya pili ni:

\[\begin{align*} \cos(2\theta)&= {\cos}^2 \theta-{\sin}^2 \theta\\[4pt] &= {\cos}^2 \theta-(1-{\cos}^2 \theta)\\[4pt] &= 2 {\cos}^2 \theta-1 \end{align*}\]

Vile vile, kupata formula mbili-angle kwa tangent, kuchukua nafasi\(\alpha=\beta=\theta\) katika formula jumla inatoa

\[\begin{align*} \tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\\[4pt] \tan(\theta+\theta)&= \dfrac{\tan \theta+\tan \theta}{1-\tan \theta \tan \theta}\\[4pt] \tan(2\theta)&= \dfrac{2\tan \theta}{1-{\tan}^2 \theta} \end{align*}\]

FORMULA ZA PEMBE MBILI

Fomu mbili za angle zimefupishwa kama ifuatavyo:

\[\begin{align} \sin(2\theta)&= 2 \sin \theta \cos \theta\\[4pt] \cos(2\theta)&= {\cos}^2 \theta-{\sin}^2 \theta =1-2 {\sin}^2 \theta = 2{\cos}^2 \theta-1\\[4pt] \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2\theta} \end{align}\]

Jinsi ya: Kutokana na tangent ya angle na quadrant ambayo iko, tumia fomu mbili za angle ili kupata thamani halisi

1. Chora pembetatu ili kutafakari habari iliyotolewa.
2. Tambua formula sahihi ya angle mbili.
3. Maadili ya mbadala katika formula kulingana na pembetatu.
4. Kurahisisha.

Mfano\(\PageIndex{1}\): Using a Double-Angle Formula to Find the Exact Value Involving Tangent

Kutokana\(\tan \theta=−\dfrac{3}{4}\) na kwamba na\(\theta\) ni katika roboduara II, kupata zifuatazo:

1. \(\sin(2\theta)\)
2. \(\cos(2\theta)\)
3. \(\tan(2\theta)\)

Suluhisho

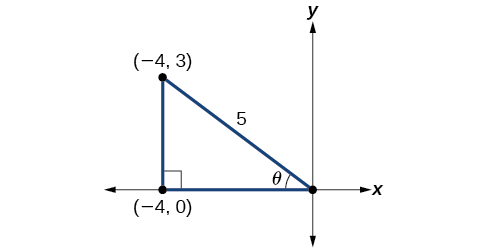
Ikiwa tunapata pembetatu ili kutafakari habari iliyotolewa, tunaweza kupata maadili yanayotakiwa kutatua matatizo kwenye picha. Tunapewa\(\tan \theta=−\dfrac{3}{4}\), kama\(\theta\) ilivyo katika quadrant II. Tangent ya angle ni sawa na upande wa pili juu ya upande wa karibu, na kwa sababu\(\theta\) iko katika roboduara ya pili, upande wa karibu ni kwenye x -axis na ni hasi. Tumia Theorem ya Pythagorean ili kupata urefu wa hypotenuse:

\[\begin{align*} {(-4)}^2+{(3)}^2&= c^2\\[4pt] 16+9&= c^2\\[4pt] 25&= c^2\\[4pt] c&= 5 \end{align*}\]

Sasa tunaweza kuteka pembetatu sawa na ile iliyoonyeshwa kwenye Kielelezo\(\PageIndex{2}\).

Kielelezo\(\PageIndex{2}\)

1. Hebu tuanze kwa kuandika formula mbili-angle kwa sine.

   \(\sin(2\theta)=2 \sin \theta \cos \theta\)

   Tunaona kwamba tunahitaji kupata\(\sin \theta\) na\(\cos \theta\). Kulingana na Kielelezo\(\PageIndex{2}\), tunaona kwamba hypotenuse ni sawa\(5\)\(\sin θ=35\), hivyo\(\sin θ=35\), na\(\cos θ=−45\). Badilisha maadili haya katika equation, na kurahisisha.

   Hivyo,

   \[\begin{align*} \sin(2\theta)&= 2\left(\dfrac{3}{5}\right)\left(-\dfrac{4}{5}\right)\\[4pt] &= -\dfrac{24}{25} \end{align*}\]

2. Andika formula mbili-angle kwa cosine.

   \(\cos(2\theta)={\cos}^2 \theta−{\sin}^2 \theta\)

   Tena, badala ya maadili ya sine na cosine katika equation, na kurahisisha.

   \[\begin{align*} \cos(2\theta)&= {\left(-\dfrac{4}{5}\right)}^2-{\left(\dfrac{3}{5}\right)}^2\\[4pt] &= \dfrac{16}{25}-\dfrac{9}{25}\\[4pt] &= \dfrac{7}{25} \end{align*}\]

3. Andika formula mbili-angle kwa tangent.

   \(\tan(2\theta)=\dfrac{2 \tan \theta}{1−{\tan}^2\theta}\)

   Katika formula hii, tunahitaji tangent, ambayo tulipewa kama\(\tan \theta=−\dfrac{3}{4}\). Badilisha thamani hii katika equation, na kurahisisha.

   \ [kuanza {align*}\ tan (2\ theta) &=\ dfrac {2\ kushoto (-\ dfrac {3} {4}\ haki)} {1- {\ kushoto (-\ dfrac {3} {4}\ haki)} ^2}\ [4pt]
   &=\ dfrac {-\ dfrac {3} {2}} {2}} 1-\ dfrac {9} {16}}\ [4pt]
   &= -\ dfrac {3} {2}\ kushoto (\ dfrac {16} {7}\ haki)\\ [4pt]
   &= -\ dfrac {24} {7}
   \ mwisho {align*}\]

Zoezi\(\PageIndex{1}\)

Kutokana\(\sin \alpha=\dfrac{5}{8}\), na\(\theta\) katika roboduara mimi, kupata\(\cos(2\alpha)\).

Jibu

\(\cos(2\alpha)=\dfrac{7}{32}\)

Mfano\(\PageIndex{2}\): Using the Double-Angle Formula for Cosine without Exact Values

Tumia formula mbili-angle kwa cosine kuandika\(\cos(6x)\) kwa suala la\(cos(3x)\).

Suluhisho

\[\begin{align*} \cos(6x)&= \cos(3x+3x)\\[4pt] &= \cos 3x \cos 3x-\sin 3x \sin 3x\\[4pt] &= {\cos}^2 3x-{\sin}^2 3x \end{align*}\]

Uchambuzi

Mfano huu unaeleza kwamba tunaweza kutumia formula mbili-angle bila kuwa na maadili halisi. Inasisitiza kuwa mfano ni kile tunachohitaji kukumbuka na kwamba utambulisho ni wa kweli kwa maadili yote katika uwanja wa kazi ya trigonometric.

Kutumia Fomu mbili za Angle ili kuthibitisha Utambulisho

Kuanzisha utambulisho kwa kutumia formula mbili-angle ni kazi kwa kutumia hatua sawa tulizotumia kupata jumla na tofauti formula. Chagua upande ngumu zaidi wa equation na uandike upya mpaka inafanana na upande wa pili.

Mfano\(\PageIndex{3}\): Using the Double-Angle Formulas to Verify an Identity

Thibitisha utambulisho wafuatayo kwa kutumia formula mbili za angle:

\[1+\sin(2\theta)={(\sin\theta+\cos\theta)}^2 \nonumber \]

Suluhisho

Tutafanya kazi upande wa kulia wa ishara sawa na kuandika tena maneno mpaka inafanana na upande wa kushoto.

\[\begin{align*} {(\sin \theta+\cos \theta)}^2&= {\sin}^2 \theta+2 \sin \theta \cos \theta+{\cos}^2 \theta\\[4pt] &= ({\sin}^2 \theta+{\cos}^2 \theta)+2 \sin \theta \cos \theta\\[4pt] &= 1+2 \sin \theta \cos \theta\\[4pt] &= 1+\sin(2\theta) \end{align*}\]

Uchambuzi

Utaratibu huu sio ngumu, kwa muda mrefu tunapokumbuka formula kamili ya mraba kutoka kwa algebra:

\[{(a\pm b)}^2=a^2\pm 2ab+b^2 \nonumber \]

wapi\(a=\sin \theta\) na\(b=\cos \theta\). Sehemu ya kufanikiwa katika hisabati ni uwezo wa kutambua ruwaza. Wakati maneno au alama zinaweza kubadilika, algebra inabakia thabiti.

Zoezi\(\PageIndex{2}\)

Thibitisha utambulisho:\({\cos}^4 \theta−{\sin}^4 \theta=\cos(2\theta)\).

Jibu

\({\cos}^4 \theta−{\sin}^4 \theta=({\cos}^2 \theta+{\sin}^2 \theta)({\cos}^2 \theta−{\sin}^2 \theta)=\cos(2\theta)\)

Mfano\(\PageIndex{4}\): Verifying a Double-Angle Identity for Tangent

Thibitisha utambulisho:\(\tan(2 \theta)=2\cot \theta−\tan \theta\)

Suluhisho

Katika kesi hii, tutafanya kazi na upande wa kushoto wa equation na kurahisisha au kuandika upya mpaka ni sawa na upande wa kulia wa equation.

\[\begin{align*} \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2 \theta} \qquad \text{Double-angle formula}\\[4pt] &= \dfrac{2 \tan \theta\left (\dfrac{1}{\tan \theta}\right)}{(1-{\tan}^2 \theta)\left (\dfrac{1}{\tan \theta}\right )} \qquad \text{Multiply by a term that results in desired numerator}\\[4pt] &= \dfrac{2}{\dfrac{1}{\tan \theta}-\dfrac{ {\tan}^2 \theta}{\tan \theta}}\\[4pt] &= \dfrac{2}{\cot \theta-\tan \theta} \qquad \text {Use reciprocal identity for } \dfrac{1}{\tan \theta} \end{align*}\]

Uchambuzi

Hapa ni kesi ambapo upande ngumu zaidi wa equation ya awali ilionekana upande wa kulia, lakini tulichagua kufanya kazi upande wa kushoto. Hata hivyo, kama tulikuwa amechagua upande wa kushoto kuandika upya, tungekuwa tukifanya kazi nyuma ili kufika equivalency. Kwa mfano, tuseme kwamba tulitaka kuonyesha

\[\begin{align*} \dfrac{2\tan \theta}{1-{\tan}^2 \theta}&= \dfrac{2}{\cot \theta-\tan \theta} \\[4pt] \text{Lets work on the right side}\\[4pt] \dfrac{2}{\cot \theta-\tan \theta}&= \frac{2}{\frac{1}{\tan \theta }-\tan \theta }\left ( \frac{\tan \theta }{\tan \theta } \right )\\[4pt] &= \dfrac{2 \tan \theta}{\dfrac{1}{\tan \theta}(\tan \theta)-\tan \theta(\tan \theta)}\\[4pt] &= \dfrac{2 \tan \theta}{1-{\tan}^2 \theta} \end{align*}\]

Wakati wa kutumia utambulisho ili kurahisisha kujieleza kwa trigonometric au kutatua equation ya trigonometric, kuna kawaida njia kadhaa kwa matokeo yaliyohitajika. Hakuna utawala uliowekwa kwa upande gani unapaswa kutumiwa. Hata hivyo, tunapaswa kuanza na miongozo iliyoelezwa mapema.

Zoezi\(\PageIndex{3}\)

Thibitisha utambulisho:\(\cos(2\theta)\cos \theta={\cos}^3 \theta−\cos \theta {\sin}^2 \theta\).

Jibu

\(\cos(2 \theta)\cos \theta=({\cos}^2 \theta−{\sin}^2 \theta) \cos \theta={\cos}^3 \theta−\cos \theta {\sin}^2 \theta\)

Tumia Fomu za Kupunguza ili kurahisisha Kuelezea

Mbili-angle formula inaweza kutumika kupata formula kupunguza, ambayo ni formula tunaweza kutumia ili kupunguza nguvu ya kujieleza kutolewa kuwashirikisha hata nguvu ya sine au cosine. Wanatuwezesha kuandika tena nguvu za sine au cosine kwa suala la nguvu ya kwanza ya cosine. Fomula hizi ni muhimu hasa katika kozi ya kiwango cha juu cha hesabu, calculus hasa. Pia huitwa formula za kupunguza nguvu, utambulisho tatu umejumuishwa na hutolewa kwa urahisi kutoka kwa fomu mbili za angle.

Tunaweza kutumia mbili ya tatu formula mbili-angle kwa cosine kupata formula kupunguza kwa sine na cosine. Hebu tuanze na\(\cos(2\theta)=1−2 {\sin}^2 \theta\). Tatua kwa\({\sin}^2 \theta\):

\[\begin{align*} \cos(2\theta)&= 1-2 {\sin}^2 \theta\\[4pt] 2 {\sin}^2 \theta&= 1-\cos(2\theta)\\[4pt] {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2} \end{align*}\]

Kisha, tunatumia formula\(\cos(2\theta)=2 {\cos}^2 \theta−1\). Tatua kwa\({\cos}^2 \theta\):

\[\begin{align*} \cos(2\theta)&= 2 {\cos}^2 \theta-1\\[4pt] 1+\cos(2\theta)&= 2 {\cos}^2 \theta\\[4pt] \dfrac{1+\cos(2\theta)}{2}&= {\cos}^2 \theta \end{align*}\]

Fomu ya mwisho ya kupunguza inatokana na kuandika tangent kwa suala la sine na cosine:

\[\begin{align*} \tan^2 \theta &= \frac{\sin^2 \theta}{\cos^2 \theta} \\[4pt] &= \dfrac{\dfrac{1-\cos(2\theta)}{2}}{\dfrac{1+\cos(2\theta)}{2}} \qquad \tag{Substitute the reduction formulas} \\[4pt] &= \left(\dfrac{1-\cos(2 \theta)}{2}\right)\left(\dfrac{2}{1+\cos(2 \theta)}\right) \\[4pt] &= \dfrac{1-\cos(2 \theta)}{1+\cos(2 \theta)} \end{align*}\]

KUPUNGUZA FORMULA

Fomu za kupunguza ni muhtasari kama ifuatavyo:

\[{\sin}^2 \theta=\dfrac{1−\cos(2 \theta)}{2}\]

\[{\cos}^2 \theta=\dfrac{1+\cos(2 \theta)}{2}\]

\[{\tan}^2 \theta=\dfrac{1−\cos(2 \theta)}{1+\cos(2 \theta)}\]

Mfano\(\PageIndex{5}\): Writing an Equivalent Expression Not Containing Powers Greater Than 1

Andika kujieleza sawa kwa\({\cos}^4 x\) kuwa haina kuhusisha mamlaka yoyote ya sine au cosine kubwa kuliko\(1\).

Suluhisho

Tutatumia formula ya kupunguza kwa cosine mara mbili.

\ [kuanza {align*}
{\ cos} ^4 x&= {({\ cos} ^2 x)} ^2\\ [4pt]
&= {\ kushoto (\ dfrac {1+\ cos (2x)} {2}\ haki)} ^2\ qquad\ maandishi {formula kupunguza badala}\\ [4pt]
&=\ dfrac {1} {4} (4} 1+2\ cos (2x) + {\ cos} ^2 (2x))\\ [4pt]
&=\ dfrac {1} {4} +\ dfrac {1} {2}\ cos (2x) +\ dfrac {1} {4}\ kushoto (\ dfrac {1+ {\ cos} ^2 (2x)} {2}\ haki)\ qquad\ maandishi {formula ya kupunguza mbadala kwa} {\ cos} ^2 x\\ [4pt]
&=\ dfrac {1} {1} {2}\ cos (2x) +\ dfrac {1} {8} +\ dfrac {1} {8}\ cos (4x)\\ [4pt]
&=\ dfrac {3} {8} +\ dfrac {1} {2}\ cos (2x) +\ dfrac {1} {8}\ cos (4x)
\ mwisho {align*}\]

Uchambuzi

Suluhisho hupatikana kwa kutumia formula ya kupunguza mara mbili, kama ilivyoelezwa, na formula kamili ya mraba kutoka kwa algebra.

Mfano\(\PageIndex{6}\): Using the Power-Reducing Formulas to Prove an Identity

Tumia formula za kupunguza nguvu ili kuthibitisha\({\sin}^3(2x)=\left[ \dfrac{1}{2} \sin(2x) \right] [ 1−\cos(4x) \)

Suluhisho

Tutafanya kazi kwa kurahisisha upande wa kushoto wa equation:

\[\begin{align*} {\sin}^3(2x)&= [\sin(2x)][{\sin}^2(2x)]\\[4pt] &= \sin(2x)\left [\dfrac{1-\cos(4x)}{2}\right ]\qquad \text{Substitute the power-reduction formula.}\\[4pt] &= \sin(2x)\left(\dfrac{1}{2}\right)[1-\cos(4x)]\\[4pt] &= \dfrac{1}{2}[\sin(2x)][1-\cos(4x)] \end{align*}\]

Uchambuzi

Kumbuka kuwa katika mfano huu,\(\dfrac{1−\cos(4x)}{2}\) tumebadilisha\({\sin}^2(2x)\). Hali ya formula\({\sin}^2 \theta=\dfrac{1−\cos(2\theta)}{2}\)

Sisi basi\(\theta=2x\), hivyo\(2\theta=4x\).

Zoezi\(\PageIndex{4}\)

Tumia formula za kupunguza nguvu ili kuthibitisha hilo\(10{\cos}^4 x=\dfrac{15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x)\).

Jibu

\[\begin{align*} 10{\cos}^4 x&= 10{({\cos}^2x)}^2\\[4pt] &= 10{\left[\dfrac{ 1+\cos(2x)}{2} \right]}^2\qquad \text{Substitute reduction formula for } {\cos}^2x\\[4pt] &= \dfrac{10}{4}[1+2\cos(2x)+{\cos}^2(2x)]\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2}\cos(2x)+\dfrac{10}{4}\left(\dfrac{1+{\cos}^2(2x)}{2}\right)\qquad \text{ Substitute reduction formula for } {\cos}^2 x\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}\]

Kutumia Fomu za Nusu-Angle ili Kupata Maadili halisi

Seti inayofuata ya utambulisho ni seti ya formula za nusu-angle, ambazo zinaweza kupatikana kutokana na fomu za kupunguza na tunaweza kutumia wakati tuna angle ambayo ni nusu ya ukubwa wa angle maalum. Kama sisi kuchukua nafasi\(\theta\) na\(\dfrac{\alpha}{2}\), nusu-angle formula kwa sine hupatikana kwa kurahisisha equation na kutatua kwa\(\sin\left(\dfrac{\alpha}{2}\right)\). Kumbuka kuwa kanuni za nusu za angle zinatanguliwa na\(\pm\) ishara. Hii haina maana kwamba maneno mazuri na mabaya ni halali. Badala yake, inategemea quadrant ambayo\(\dfrac{\alpha}{2}\) inakoma.

Fomu ya nusu ya angle ya sine inatokana kama ifuatavyo:

\[\begin{align*} {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2}\\[4pt] {\sin}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\left(\cos 2\cdot \dfrac{\alpha}{2}\right)}{2}\\[4pt] &= \dfrac{1-\cos \alpha}{2}\\[4pt] \sin \left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}} \end{align*}\]

Kupata formula nusu-angle kwa cosine, tuna

\[\begin{align*} {\cos}^2 \theta&= \dfrac{1+\cos(2\theta)}{2}\\[4pt] {\cos}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{2}\\[4pt] &= \dfrac{1+\cos \alpha}{2}\\[4pt] \cos\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}} \end{align*}\]

Kwa utambulisho tangent, tuna

\[\begin{align*} {\tan}^2 \theta&= \dfrac{1-\cos(2\theta)}{1+\cos(2\theta)}\\[4pt] {\tan}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}\\[4pt] \tan\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} \end{align*}\]

NUSU ANGLE FORMULA

Fomu za nusu-angle ni kama ifuatavyo:

\[\begin{align} \sin\left(\dfrac{\alpha}{2}\right)&=\pm \sqrt{\dfrac{1-\cos \alpha}{2}} \label{halfsine} \\[4pt] \cos \left(\dfrac{\alpha}{2} \right) &=\pm \sqrt{\dfrac{1+\cos \alpha}{2}} \\[4pt] \tan\left(\dfrac{\alpha}{2}\right) &=\pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} =\dfrac{\sin \alpha}{1+\cos \alpha} =\dfrac{1-\cos \alpha}{\sin \alpha}\end{align}\]

Mfano\(\PageIndex{7}\)

Kutumia Mfumo wa Nusu-Angle ili Kupata Thamani halisi ya Kazi ya Sine. Pata\(\sin(15°)\) kutumia formula ya nusu ya angle.

Suluhisho

Tangu\(15°=\dfrac{30°}{2}\), tunatumia formula ya nusu-angle kwa sine (Equation\ ref {halfsine}):

\ [kuanza {align*}
\ dhambi\ dfrac {30^ {\ circ}} {2} &=\ sqrt {\ dfrac {1-\ cos 30^ {\ circ}} {2}}\ [4pt]
&=\ sqrt {1-\ dfrac {\ sqrt {3}} {2}} {2}}\\ [4pt]
&=\ sqrt {\ drac {\ drac {2-\ sqrt {3}} {2}} {2}}\\ [4pt]
&=\ sqrt {2-\ sqrt {3}} {4}}\\ [4pt]
&=\ drac {\ sqrt {2-\ sqrt {3}}} {2}
\ mwisho {align*}\]

Kumbuka kwamba tunaweza kuangalia jibu kwa calculator graphing.

Uchambuzi

Kumbuka kwamba tulitumia tu mizizi chanya kwa sababu\(\sin(15°)\) ni chanya.

Jinsi ya: Kutokana na tangent ya angle na quadrant ambayo angle iko, kupata maadili halisi ya kazi trigonometric ya nusu ya angle.

1. Chora pembetatu ili kuwakilisha taarifa iliyotolewa.
2. Tambua formula sahihi ya nusu ya angle.
3. Maadili ya mbadala katika formula kulingana na pembetatu.
4. Kurahisisha.

Mfano\(\PageIndex{8}\): Finding Exact Values Using Half-Angle Identities

Kutokana\(\tan \alpha=\dfrac{8}{15}\) na hilo na\(α\) liko katika quadrant III, pata thamani halisi ya yafuatayo:

1. \(\sin\left(\dfrac{\alpha}{2}\right)\)
2. \(\cos\left(\dfrac{\alpha}{2}\right)\)
3. \(\tan\left(\dfrac{\alpha}{2}\right)\)

Suluhisho

Kutumia taarifa iliyotolewa, tunaweza kuteka pembetatu iliyoonyeshwa kwenye Kielelezo\(\PageIndex{3}\). Kutumia Theorem ya Pythagorean, tunapata hypotenuse kuwa 17. Kwa hiyo, tunaweza kuhesabu\(\sin \alpha=−\dfrac{8}{17}\) na\(\cos \alpha=−\dfrac{15}{17}\).

Kielelezo\(\PageIndex{3}\)

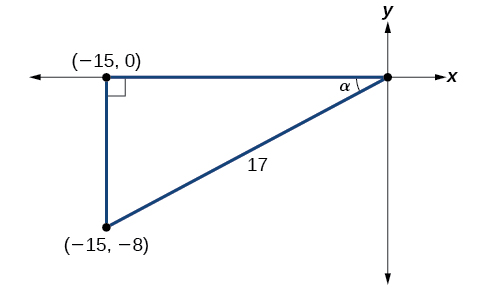
1. Kabla ya kuanza, tunapaswa kukumbuka kwamba ikiwa\(α\) iko katika quadrant III, basi\(180°<\alpha<270°\), hivyo\(\dfrac{180°}{2}<\dfrac{\alpha}{2}<\dfrac{270°}{2}\). Hii ina maana kwamba upande terminal ya\(\dfrac{\alpha}{2}\) ni katika roboduara II, tangu\(90°<\dfrac{\alpha}{2}<135°\). Ili kupata\(\sin \dfrac{\alpha}{2}\), tunaanza kwa kuandika formula ya nusu-angle kwa sine. Kisha sisi badala ya thamani ya cosine tuliyopata kutoka pembetatu katika Kielelezo\(\PageIndex{3}\) na kurahisisha. \[\begin{align*} \sin \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1-(-\dfrac{15}{17})}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{2}}\\[4pt] &= \pm \sqrt{\dfrac{32}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{16}{17}}\\[4pt] &= \pm \dfrac{4}{\sqrt{17}}\\[4pt] &= \dfrac{4\sqrt{17}}{17} \end{align*}\]Sisi kuchagua thamani chanya ya\(\sin \dfrac{\alpha}{2}\) sababu angle huisha katika roboduara II na sine ni chanya katika roboduara II.
2. Ili kupata\(\cos \dfrac{\alpha}{2}\), tutaandika formula ya nusu-angle kwa cosine, badala ya thamani ya cosine tuliyopata kutoka pembetatu kwenye Kielelezo\(\PageIndex{3}\), na kurahisisha. \[\begin{align*} \cos \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1+\left(-\dfrac{15}{17}\right)}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{2}{17}}{2}}\\[4pt] &= \pm \sqrt{\dfrac{2}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1}{17}}\\[4pt] &= -\dfrac{\sqrt{17}}{17} \end{align*}\]Sisi kuchagua thamani hasi ya\(\cos \dfrac{\alpha}{2}\) sababu angle ni katika roboduara II kwa sababu cosine ni hasi katika roboduara II.
3. Ili kupata\(\tan \dfrac{\alpha}{2}\), tunaandika formula ya nusu-angle kwa tangent. Tena, tunabadilisha thamani ya cosine tuliyopata kutoka pembetatu kwenye Kielelezo\(\PageIndex{3}\) na kurahisisha. \[\begin{align*} \tan \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}}\\[4pt] &= \pm \sqrt{\dfrac{1-\left(-\dfrac{15}{17}\right)}{1+\left(-\dfrac{15}{17}\right)}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{\dfrac{2}{17}}}\\[4pt] &= \pm \sqrt{\dfrac{32}{2}}\\[4pt] &= -\sqrt{16}\\[4pt] &= -4 \end{align*}\]Sisi kuchagua thamani hasi ya\(\tan \dfrac{\alpha}{2}\) sababu\(\dfrac{\alpha}{2}\) liko katika roboduara II, na tangent ni hasi katika roboduara II.

Zoezi\(\PageIndex{5}\)

Kutokana\(\sin \alpha=−\dfrac{4}{5}\) na kwamba na\(\alpha\) uongo katika roboduara IV, kupata thamani halisi ya\(\cos \left(\dfrac{\alpha}{2}\right)\).

Jibu

\(-\dfrac{2}{\sqrt{5}}\)

Mfano\(\PageIndex{9}\): Finding the Measurement of a Half Angle

Sasa, tutarudi kwenye tatizo lililofanywa mwanzoni mwa sehemu hiyo. Njia ya baiskeli inajengwa kwa ushindani wa kiwango cha juu na angle ya\(θ\) sumu na barabara na ardhi. Njia panda nyingine ni kuwa ujenzi nusu kama mwinuko kwa ajili ya ushindani novice. Ikiwa\(tan θ=53\) kwa ushindani wa ngazi ya juu, ni kipimo gani cha angle kwa ushindani wa novice?

Suluhisho

Kwa kuwa angle ya ushindani wa novice hatua nusu mwinuko wa angle kwa ushindani wa ngazi ya juu, na\(\tan \theta=\dfrac{5}{3}\) kwa ushindani mkubwa, tunaweza kupata\(\cos \theta\) kutoka pembetatu sahihi na Theorem ya Pythagorean ili tuweze kutumia utambulisho wa nusu angle. Angalia Kielelezo\(\PageIndex{4}\).

\[\begin{align*} 3^2+5^2&=34\\[4pt] c&=\sqrt{34} \end{align*}\]

Kielelezo\(\PageIndex{4}\)

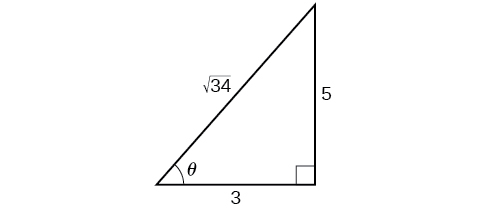
Tunaona kwamba\(\cos \theta=\dfrac{3}{\sqrt{34}}=\dfrac{3\sqrt{34}}{34}\). Tunaweza kutumia formula ya nusu-angle kwa tangent:\(\tan \dfrac{\theta}{2}=\sqrt{\dfrac{1−\cos \theta}{1+\cos \theta}}\). Tangu\(\tan \theta\) ni katika quadrant ya kwanza, ndivyo ilivyo\(\tan \dfrac{\theta}{2}\).

\ [kuanza {align*}
\ tan\ dfrac {\ theta} {2} &=\ sqrt {\ drac {1-\ drac {3\ sqrt {34}} {1+\ drac {3\ sqrt {34}} {34}}\ [4pt]
&=\ sqrt {\ drac {\ drac {\ drac {34-3\ sqrt {34}} {34}} {\ drac {34+3\ sqrt {34}} {34}}\ [4pt]
&=\ sqrt {34-3\ sqrt {34}} {34+3\ sqrt {34}}}\ [4pt]
&\ takriban 0.57
\ mwisho {align*}\]

Tunaweza kuchukua tangent inverse kupata angle:\({\tan}^{−1}(0.57)≈29.7°\). Hivyo angle ya barabara ya ushindani wa novice ni\(≈29.7°\).

Media

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na fomu mbili, nusu ya angle, na kupunguza.

• Utambulisho wa Pembe mbili
• Utambulisho wa nusu Angle

Mlinganyo muhimu

Fomu mbili za angle	\(\sin(2\theta)=2\sin \theta \cos \theta\) \(\cos(2\theta)={\cos}^2 \theta−{\sin}^2 \theta\) \(=1−2{\sin}^2 \theta\) \(=2{\cos}^2 \theta−1\) \(\tan(2\theta)=\dfrac{2\tan \theta}{1−{\tan}^2 \theta}\)
Kupunguza formula	\({\sin}^2 \theta=\dfrac{1−\cos(2\theta)}{2}\) \({\cos}^2 \theta=\dfrac{1+\cos(2\theta)}{2}\) \({\tan}^2 \theta=\dfrac{1−\cos(2\theta)}{1+\cos(2\theta)}\)
Nusu-angle formula	\(\sin \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{2}}\) \(\cos \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}\) \(\tan \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{1+\cos \alpha}}\) \(=\dfrac{\sin \alpha}{1+\cos \alpha}\) \(=\dfrac{1−\cos \alpha}{\sin \alpha}\)

Dhana muhimu

• Utambulisho wa pembeni mbili hutokana na kanuni za jumla za kazi za msingi za trigonometric: sine, cosine, na tangent. Angalia Mfano\(\PageIndex{1}\), Mfano\(\PageIndex{2}\), Mfano\(\PageIndex{3}\), na Mfano\(\PageIndex{4}\).
• Njia za kupunguza ni muhimu hasa katika calculus, kwa vile zinatuwezesha kupunguza nguvu ya muda wa trigonometric. Angalia Mfano\(\PageIndex{5}\) na Mfano\(\PageIndex{6}\).
• Njia za nusu za angle zinatuwezesha kupata thamani ya kazi za trigonometric zinazohusisha pembe za nusu, ikiwa angle ya awali inajulikana au la. Angalia Mfano\(\PageIndex{7}\), Mfano\(\PageIndex{8}\), na Mfano\(\PageIndex{9}\).