3.7: Kazi za busara

Last updated
Save as PDF

Page ID: 181248

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Kutumia arrow nukuu.
Tatua matatizo yaliyotumika yanayohusisha kazi za busara.
Pata nyanja za kazi za busara.
Tambua asymptotes wima.
Tambua asymptotes ya usawa.
Grafu kazi za busara.

Tuseme tunajua kwamba gharama ya kufanya bidhaa inategemea idadi ya vitu$x$, zinazozalishwa. Hii ni iliyotolewa na equation$C (x)=15,000x−0.1x^2+1000.$ Kama tunataka kujua wastani wa gharama kwa ajili ya kuzalisha$x$ vitu, tunataka kugawanya gharama kazi na idadi ya vitu,$x$. Kazi ya wastani ya gharama, ambayo hutoa gharama ya wastani kwa kila kitu kwa$x$ vitu zinazozalishwa, ni

\[f(x)=\dfrac{15,000x−0.1x^2+1000}{x} \nonumber\]

Matatizo mengine mengi ya maombi yanahitaji kutafuta thamani ya wastani kwa namna hiyo, kutupa vigezo katika denominator. Imeandikwa bila kutofautiana katika denominator, kazi hii itakuwa na nguvu hasi integer.

Katika sehemu chache zilizopita, tumefanya kazi na kazi za polynomial, ambazo ni kazi na integers zisizo hasi kwa watazamaji. Katika sehemu hii, tunachunguza kazi za busara, ambazo zina vigezo katika denominator.

Kutumia Arrow Nukuu

Tumeona grafu ya kazi ya msingi ya usawa na kazi ya usawa ya mraba kutoka kwa utafiti wetu wa kazi za toolkit. Kuchunguza grafu hizi, kama inavyoonekana katika Kielelezo$\PageIndex{1}$, na taarifa baadhi ya vipengele vyao.

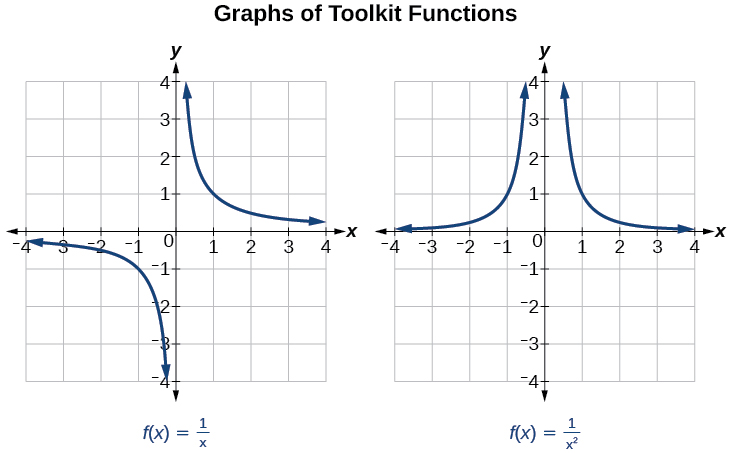
Grafu ya f (x) =1/x na f (x) =1/x ^ 2 — Kielelezo$\PageIndex{1}$

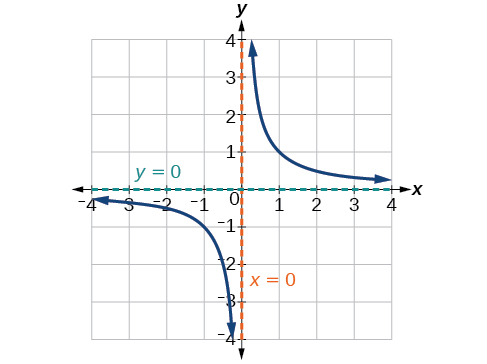
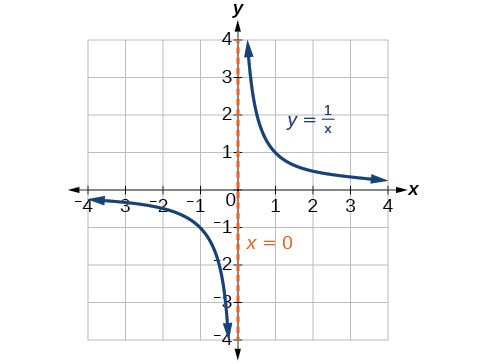
Mambo kadhaa ni dhahiri kama sisi kuchunguza grafu ya$f(x)=\frac{1}{x}$.

Kwenye tawi la kushoto la grafu, safu inakaribia$x$ -axis$(y=0)$ kama$x\rightarrow -\infty$.
Kama grafu inakaribia$x = 0$ kutoka upande wa kushoto, matone ya curve, lakini tunapokaribia sifuri kutoka kulia, safu inaongezeka.
Hatimaye, kwenye tawi la kulia la grafu, curves inakaribia$x$ -axis$(y=0) $ kama$x\rightarrow \infty$.

Kwa muhtasari, tunatumia nukuu ya mshale ili kuonyesha kwamba$x$ au$f (x)$ inakaribia thamani fulani (Jedwali$\PageIndex{1}$).

Jedwali$\PageIndex{1}$
Mkono	Maana
$x\rightarrow a^-$	$x$inakaribia kutoka upande wa kushoto ($x<a$lakini karibu na$a$)
$x\rightarrow a^+$	$x$mbinu kutoka kulia ($x>a$lakini karibu na$a$)
$x\rightarrow \infty$	$x$inakaribia infinity ($x$huongezeka bila kufungwa)
$x\rightarrow −\infty$	$x$inakaribia infinity hasi ($x$itapungua bila kufungwa)
$f(x)\rightarrow \infty$	pato inakaribia infinity (pato huongezeka bila kufungwa)
$f(x)\rightarrow −\infty$	pato inakaribia infinity hasi (pato hupungua bila kufungwa)
$f(x)\rightarrow a$	mbinu za pato$a$

Tabia ya Mitaa ya$f(x)=\frac{1}{x}$

Hebu tuanze kwa kuangalia kazi ya usawa,$f(x)=\frac{1}{x}$. Hatuwezi kugawanya na sifuri, ambayo ina maana kazi ni undefined katika$x=0$; hivyo sifuri si katika uwanja. Kama maadili ya pembejeo yanakaribia sifuri kutoka upande wa kushoto (kuwa ndogo sana, maadili hasi), maadili ya kazi hupungua bila kufungwa (kwa maneno mengine, wanakaribia infinity hasi). Tunaweza kuona tabia hii katika Jedwali$\PageIndex{2}$.

Jedwali$\PageIndex{2}$
$x$	—0.1	—0.01	—0.001	— 0.0001
$f(x)=\frac{1}{x}$	—10	—100	—1000	—10,000

Tunaandika kwa nukuu ya mshale

kama$x\rightarrow 0^−,f(x)\rightarrow −\infty$

Kama maadili ya pembejeo yanakaribia sifuri kutoka upande wa kulia (kuwa ndogo sana, maadili mazuri), maadili ya kazi huongezeka bila kufungwa (inakaribia infinity). Tunaweza kuona tabia hii katika Jedwali$\PageIndex{3}$.

Jedwali$\PageIndex{3}$
$x$	0.1	0.01	0.001	0.0001
$f(x)=\frac{1}{x}$	10	100	1000	10,000

Tunaandika kwa nukuu ya mshale

Kama$x\rightarrow 0^+, f(x)\rightarrow \infty$.

Angalia Kielelezo$\PageIndex{2}$.

Grafu ya f (x) =1/x ambayo inaashiria tabia ya mwisho. Kama x inakwenda infinity hasi, f (x) inakwenda 0, na kama x inakwenda 0^-, f (x) inakwenda infinity hasi. Kama x inakwenda infinity chanya, f (x) inakwenda 0, na kama x inakwenda 0 ^ +, f (x) inakwenda infinity chanya. — Kielelezo$\PageIndex{2}$.

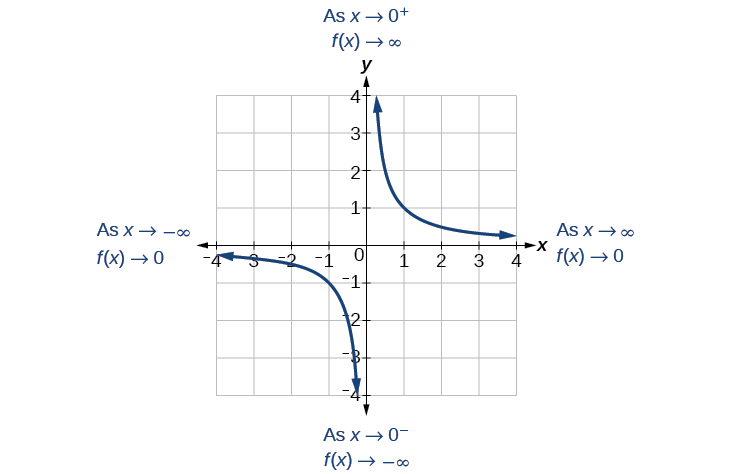
Tabia hii inajenga asymptote ya wima, ambayo ni mstari wa wima ambao grafu inakaribia lakini kamwe huvuka. Katika kesi hii, grafu inakaribia mstari wa wima$x=0$ kama pembejeo inakuwa karibu na sifuri (Kielelezo$\PageIndex{3}$).

Grafu ya f (x) =1/x na asymptote yake ya wima katika x=0. — Kielelezo$\PageIndex{3}$.

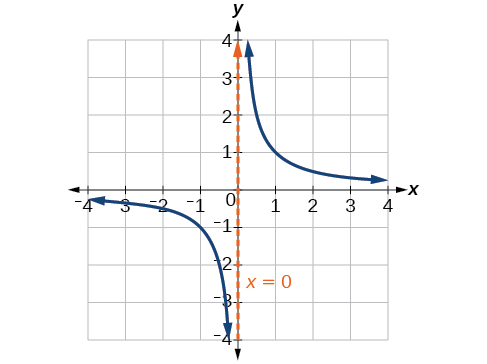
Ufafanuzi: VERTICAL ASYMPTOTE

Asymptote ya wima ya grafu ni mstari wa wima$x=a$ ambapo grafu huelekea kwenye infinity chanya au hasi kama mbinu za pembejeo$a$. Tunaandika

Kama$x\rightarrow a$,$f(x)\rightarrow \infty$, au kama$x\rightarrow a$,$f(x)\rightarrow −\infty$.

Mwisho Tabia ya$f(x)=\frac{1}{x}$

Kama maadili ya infinity$x$ mbinu, kazi maadili mbinu$0$. Kama maadili ya$x$ mbinu infinity hasi, kazi maadili mbinu$0$ (Kielelezo$\PageIndex{4}$). Kwa mfano, kwa kutumia nukuu ya mshale

Kama$x\rightarrow \infty$,$f(x)\rightarrow 0$, na kama$x\rightarrow −\infty$,$f(x)\rightarrow 0$.

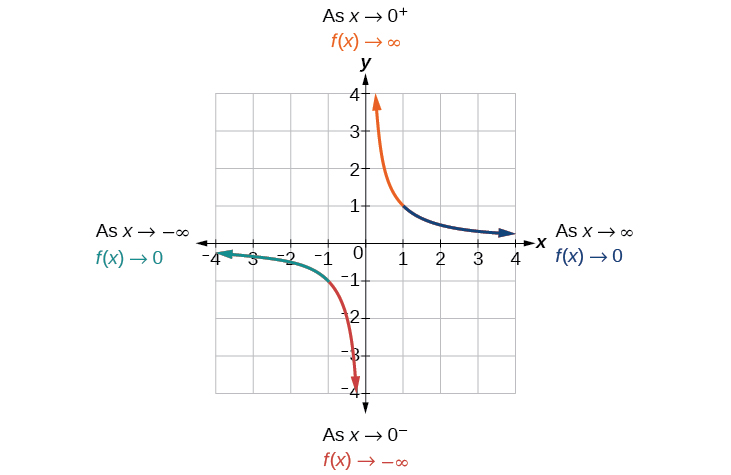
Grafu ya f (x) =1/x ambayo inaonyesha makundi ya pointi za kugeuka ili kuonyesha tabia yao ya mwisho. — Kielelezo$\PageIndex{4}$.

Kulingana na tabia hii ya jumla na grafu, tunaweza kuona kwamba kazi mbinu 0 lakini kamwe kweli fika 0; inaonekana ngazi mbali kama pembejeo kuwa kubwa. Tabia hii inajenga asymptote ya usawa, mstari usio na usawa ambao grafu inakaribia kama ongezeko la pembejeo au hupungua bila kufungwa. Katika kesi hii, grafu inakaribia mstari usio na usawa$y=0$. Angalia Kielelezo$\PageIndex{5}$.

Grafu ya f (x) =1/x na asymptote yake ya wima katika x=0 na asymptote yake ya usawa katika y=0. — Kielelezo$\PageIndex{5}$.

Ufafanuzi: USAWA ASYMPTOTE

Asymptote ya usawa ya grafu ni mstari usio na usawa$y=b$ ambapo grafu inakaribia mstari kama pembejeo zinaongezeka au kupungua bila kufungwa. Tunaandika

Kama$x\rightarrow \infty \text{ or } x\rightarrow −\infty$,$f(x)\rightarrow b$.

Mfano$\PageIndex{1}$: Using Arrow Notation.

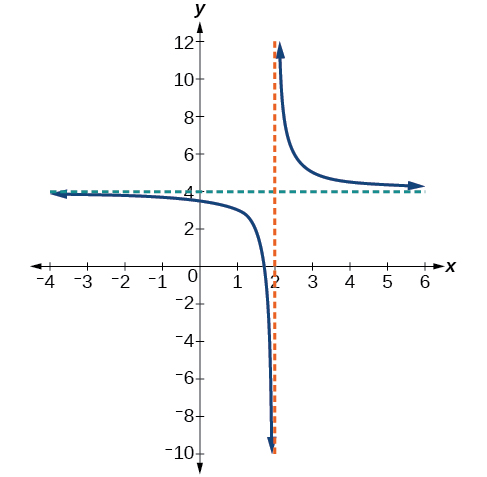
Matumizi arrow nukuu kuelezea tabia ya mwisho na tabia ya ndani ya kazi graphed katika Kielelezo$\PageIndex{6}$.

Grafu ya f (x) =1/ (x-2) +4 na asymptote yake ya wima saa x=2 na asymptote yake ya usawa katika y=4. — Kielelezo$\PageIndex{6}$.

Suluhisho

Kumbuka kwamba grafu inaonyesha asymptote wima katika$x=2$, ambayo inatuambia kwamba kazi haijulikani katika$x=2$.

Kama$x\rightarrow 2^−$,$f(x)\rightarrow −\infty,$ na kama$x\rightarrow 2^+$,$f(x)\rightarrow \infty$.

Na kama pembejeo kupungua bila amefungwa, grafu inaonekana kuwa leveling mbali katika maadili pato la$4$, kuonyesha asymptote usawa katika$y=4$. Kama pembejeo zinaongezeka bila kufungwa, viwango vya grafu huondoka$4$.

Kama$x\rightarrow \infty$,$f(x)\rightarrow 4$ na kama$x\rightarrow −\infty$,$f(x)\rightarrow 4$.

Mazoezi$\PageIndex{1}$

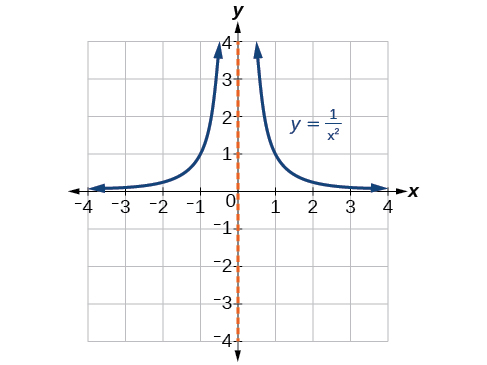
Tumia alama ya mshale kuelezea tabia ya mwisho na tabia za mitaa kwa kazi ya mraba ya usawa.

Jibu

Mwisho tabia: kama$x\rightarrow \pm \infty$,$f(x)\rightarrow 0$;

Tabia za mitaa: kama$x\rightarrow 0$,$f(x)\rightarrow \infty$ (hakuna x- au y-intercepts)

Mfano$\PageIndex{2}$: Using Transformations to Graph a Rational Function.

Mchoro grafu ya kazi ya usawa ilibadilisha vitengo viwili upande wa kushoto na hadi vitengo vitatu. Tambua asymptotes ya usawa na wima ya grafu, ikiwa ipo.

Suluhisho

Kuhamisha grafu kushoto 2 hadi 3 ingeweza kusababisha kazi

\[f(x)=\dfrac{1}{x+2}+3\]

au equivalently, kwa kutoa maneno denominator ya kawaida,

\[f(x)=\dfrac{3x+7}{x+2}\]

Grafu ya kazi iliyobadilishwa imeonyeshwa kwenye Kielelezo$\PageIndex{7}$.

Grafu ya f (x) =1/ (x+2) +3 na asymptote yake ya wima saa x=-2 na asymptote yake ya usawa katika y=3. — Kielelezo$\PageIndex{7}$.

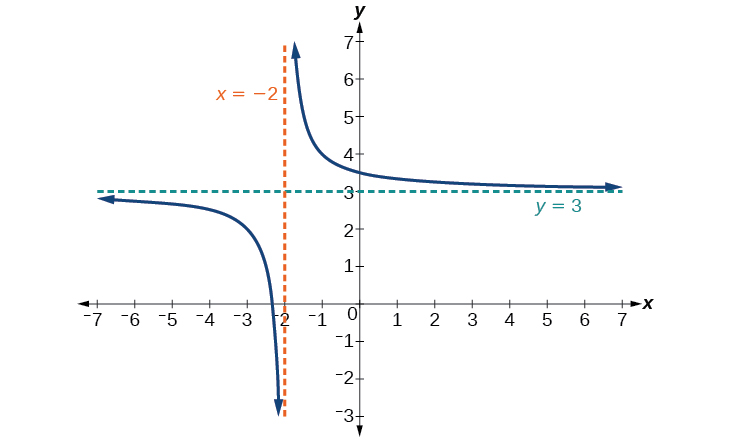
Kumbuka kwamba kazi hii haijulikani$x=−2$, na grafu pia inaonyesha asymptote wima katika$x=−2$.

Kama$x\rightarrow −2^−$,$f(x)\rightarrow −\infty$, na kama$x\rightarrow −2^+$,$f(x)\rightarrow \infty$.

Kama pembejeo zinaongezeka na kupungua bila kufungwa, grafu inaonekana kuwa inazidi kuongezeka kwa maadili ya pato ya 3, kuonyesha asymptote ya usawa$y=3$.

Kama$x\rightarrow \pm \infty$,$f(x)\rightarrow 3$.

Uchambuzi

Kumbuka kwamba asymptotes usawa na wima ni kubadilishwa kushoto 2 kuendelea 3 pamoja na kazi.

Zoezi$\PageIndex{2}$

Mchoro grafu, na upate asymptotes ya usawa na wima ya kazi ya mraba ya usawa ambayo imebadilishwa vitengo 3 na vitengo vya chini vya 4.

Suluhisho

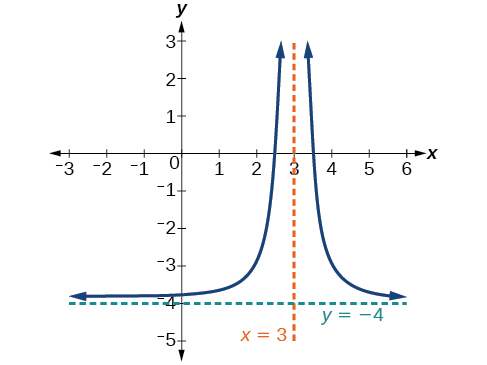
Grafu ya f (x) =1/ (x-3) ^2-4 na asymptote yake ya wima saa x=3 na asymptote yake ya usawa katika y=-4. — Kielelezo$\PageIndex{8}$.

Kazi na asymptotes hubadilishwa vitengo 3 haki na vitengo 4 chini. Kama$x\rightarrow 3$, $f(x)\rightarrow \infty$, and as $x\rightarrow \pm \infty$, $f(x)\rightarrow −4$.

Kazi ni$f(x)=\frac{1}{{(x−3)}^2}−4$.

Kutatua Matatizo yaliyotumika Kuhusisha Kazi za busara

Katika Mfano$\PageIndex{2}$, sisi kubadilishwa kazi toolkit kwa njia ambayo ilisababisha kazi$f(x)=\frac{3x+7}{x+2}$. Hii ni mfano wa kazi ya busara. Kazi ya busara ni kazi ambayo inaweza kuandikwa kama quotient ya kazi mbili za polynomial. Matatizo mengi ya ulimwengu halisi yanahitaji sisi kupata uwiano wa kazi mbili za polynomial. Matatizo yanayohusisha viwango na viwango mara nyingi huhusisha kazi za busara.

Ufafanuzi: KAZI YA MANUFAA

Kazi ya busara ni kazi ambayo inaweza kuandikwa kama quotient ya kazi mbili za polynomial$P(x)$ na$Q(x)$.

\[f(x)=\dfrac{P(x)}{Q(x)}=\dfrac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0},\space Q(x)≠0\]

Mfano$\PageIndex{3}$: Solving an Applied Problem Involving a Rational Function

Tangi kubwa ya kuchanganya sasa ina galoni 100 za maji ambayo paundi 5 za sukari zimechanganywa. Bomba litafungua kumwagilia galoni 10 kwa dakika ya maji ndani ya tangi wakati huo huo sukari hutiwa ndani ya tangi kwa kiwango cha pound 1 kwa dakika. Kupata mkusanyiko (paundi kwa kila lita) ya sukari katika tank baada ya dakika 12. Je, hiyo ni mkusanyiko mkubwa kuliko mwanzoni?

Suluhisho

Hebu kuwa idadi ya dakika tangu bomba kufunguliwa. Kwa kuwa maji huongezeka kwa galoni 10 kwa dakika, na sukari huongezeka kwa pound 1 kwa dakika, haya ni viwango vya mabadiliko ya mara kwa mara. Hii inatuambia kiasi cha maji katika tangi kinabadilika kwa mstari, kama vile kiasi cha sukari katika tangi. Tunaweza kuandika equation kwa kujitegemea kwa kila:

maji:$W(t)=100+10t$ katika galoni

sukari:$S(t)=5+1t$ kwa paundi

Mkusanyiko,$C$, itakuwa uwiano wa paundi ya sukari kwa galoni ya maji

\[C(t)=\dfrac{5+t}{100+10t}\]

Mkusanyiko baada ya dakika 12 hutolewa kwa kutathmini$C(t)$ saa$t= 12$.

\[\begin{align} C(12) & =\dfrac{5+12}{100+10(12)} \\ &= \dfrac{17}{220} \end{align} \]

Hii inamaanisha mkusanyiko ni paundi 17 za sukari hadi galoni 220 za maji.

Mwanzoni, ukolezi ni

\[\begin{align} C(0) & =\dfrac{5+0}{100+10(0)} \\ & =\dfrac{1}{20} \end{align} \]

Tangu$\frac{17}{220}≈0.08>\frac{1}{20}=0.05$, mkusanyiko ni mkubwa baada ya dakika 12 kuliko mwanzo.

Uchambuzi

Ili kupata asymptote ya usawa, ugawanye mgawo wa kuongoza katika nambari kwa mgawo wa kuongoza katika denominator:

\[\dfrac{1}{10}=0.1\]

Angalia asymptote ya usawa ni$y= 0.1.$ Hii inamaanisha mkusanyiko, uwiano$C,$ wa paundi za sukari hadi galoni za maji, utafikia 0.1 kwa muda mrefu.

Zoezi$\PageIndex{3}$

Kuna 1,200 freshmen na 1,500 sophomores katika mkutano wa hadhara prep saa sita mchana. Baada ya saa 12 p.m., 20 freshmen kufika katika mkutano wa hadhara kila baada ya dakika tano wakati 15 sophomores kuondoka mkutano wa hadhara. Pata uwiano wa freshmen kwa sophomores saa 1 p.m.

Jibu: $\frac{12}{11}$

Kutafuta Domains ya Kazi za busara

Asymptote ya wima inawakilisha thamani ambayo kazi ya busara haijulikani, hivyo thamani hiyo sio katika uwanja wa kazi. Kazi ya kurudisha haiwezi kuwa na maadili katika uwanja wake ambayo husababisha denominator kuwa sifuri sawa. Kwa ujumla, ili kupata uwanja wa kazi ya busara, tunahitaji kuamua ni pembejeo gani zinazosababisha mgawanyiko kwa sifuri.

Ufafanuzi: DOMAIN YA KAZI YA busara

Kikoa cha kazi ya busara kinajumuisha namba zote halisi isipokuwa zile zinazosababisha denominator kuwa sifuri sawa.

Jinsi ya: Kutokana na kazi ya busara, tafuta kikoa.

Weka denominator sawa na sifuri.
Tatua kupata maadili ya x-ambayo husababisha denominator kwa sifuri sawa.
Kikoa ni namba zote halisi isipokuwa zile zinazopatikana katika Hatua ya 2.

Mfano$\PageIndex{4}$: Finding the Domain of a Rational Function

Kupata uwanja wa$f(x)=\dfrac{x+3}{x^2−9}$.

Suluhisho

Anza kwa kuweka denominator sawa na sifuri na kutatua.

\[x^2-9=0 \nonumber \]

\[x^2=9 \nonumber \]\[x=\pm 3 \nonumber \]

Denominator ni sawa na sifuri wakati$x=\pm 3$. Kikoa cha kazi ni namba zote halisi isipokuwa$x=\pm 3$.

Uchambuzi

Grafu ya kazi hii, kama inavyoonekana katika Kielelezo$\PageIndex{9}$, inathibitisha kwamba kazi haijafafanuliwa wakati$x=\pm 3$.

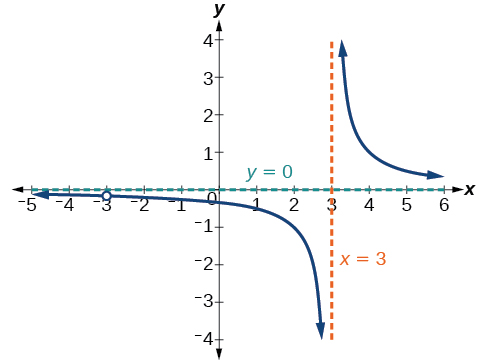
Grafu ya f (x) =1/ (x-3) na asymptote yake ya wima saa x=3 na asymptote yake ya usawa katika y=0. — Kielelezo$\PageIndex{9}$.

Kuna asymptote wima katika$x=3$ na shimo katika grafu katika$x=−3$. Tutazungumzia aina hizi za mashimo kwa undani zaidi baadaye katika sehemu hii.

Zoezi$\PageIndex{4}$

Kupata uwanja wa$f(x)=\dfrac{4x}{5(x−1)(x−5)}$.

Jibu: Kikoa ni namba zote halisi isipokuwa$x=1$ na$x=5$.

Kutambua Asymptotes ya Wima ya Kazi za Bora

Kwa kuangalia grafu ya kazi ya busara, tunaweza kuchunguza tabia yake ya ndani na kuona kwa urahisi ikiwa kuna asymptotes. Tunaweza hata kuwa na uwezo wa takriban eneo lao. Hata bila grafu, hata hivyo, tunaweza bado kuamua kama kazi ya busara iliyotolewa ina asymptotes yoyote, na kuhesabu eneo lao.

Asymptotes ya wima

Asymptotes wima ya kazi ya busara inaweza kupatikana kwa kuchunguza mambo ya denominator ambayo si ya kawaida kwa sababu katika namba. Asymptotes ya wima hutokea kwenye zero za mambo kama hayo.

Jinsi ya: Kutokana na kazi ya busara, tambua asymptotes yoyote ya wima ya grafu yake

Fanya namba na denominator.
Angalia vikwazo vyovyote katika uwanja wa kazi.
Kupunguza maneno kwa kufuta mambo ya kawaida katika nambari na denominator.
Kumbuka maadili yoyote yanayosababisha denominator kuwa sifuri katika toleo hili kilichorahisishwa. Hizi ndio ambapo asymptotes ya wima hutokea.
Angalia vikwazo vyovyote katika uwanja ambapo asymptotes haitoke. Hizi ni discontinuities removable, au “mashimo.”

Mfano$\PageIndex{5}$: Identifying Vertical Asymptotes

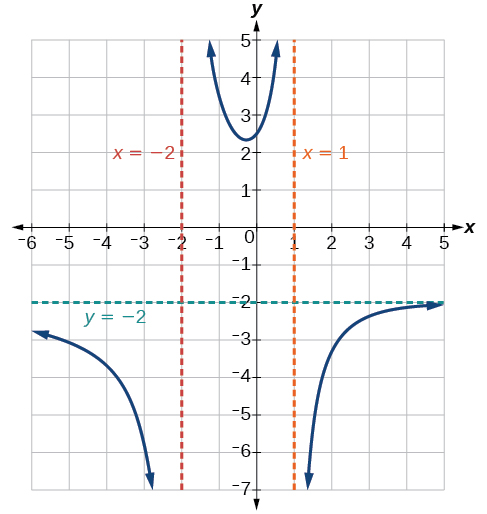
Kupata asymptotes wima ya grafu ya$k(x)=\dfrac{5+2x^2}{2−x−x^2}$.

Suluhisho

Kwanza, fikiria namba na denominator.

\[k(x)=\dfrac{5+2x^2}{2−x−x^2} \nonumber \]

\[=\dfrac{5+2x^2}{(2+x)(1-x)} \nonumber \]

Ili kupata asymptotes wima, tunaamua ambapo kazi hii itakuwa haijulikani kwa kuweka denominator sawa na sifuri:

\[(2+x)(1−x)=0 \nonumber \]

\[x=−2, \; x=1 \nonumber \]

$x=–2$Wala$x=1$ sio zero za nambari, hivyo maadili mawili yanaonyesha asymptotes mbili za wima. Grafu katika Kielelezo$\PageIndex{10}$ inathibitisha eneo la asymptotes mbili za wima.

$Grafu ya k (x) = (5+2x) ^2/ (2-x-x ^ 2) na asymptots yake ya wima saa x=-2 na x=1 na asymptote yake ya usawa katika y=-2.$

Kielelezo$\PageIndex{10}$.

Discontinuities inayoondolewa

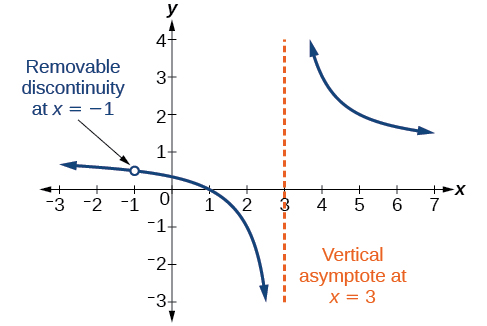
Mara kwa mara, grafu itakuwa na shimo: hatua moja ambapo grafu haijafafanuliwa, imeonyeshwa na mduara wazi. Tunaita shimo hilo kuwa discontinuity inayoondolewa. Kwa mfano, kazi$f(x)=\dfrac{x^2−1}{x^2−2x−3}$ inaweza kuandikwa tena kwa kuzingatia nambari na denominator.

\[f(x)=\dfrac{(x+1)(x−1)}{(x+1)(x−3)} \nonumber \]

Angalia kwamba$x+1$ ni jambo la kawaida kwa nambari na denominator. Zero ya jambo hili$x=−1$, ni eneo la kuacha kutolewa. Angalia pia kwamba$ (x–3) $ si sababu katika nambari zote mbili na denominator. Zero ya jambo hili$x=3$, ni asymptote ya wima. Angalia Kielelezo$\PageIndex{11}$. [Kumbuka kuwa discontinuities removable inaweza kuonekana wakati sisi kutumia graphing calculator, kulingana na dirisha kuchaguliwa.]

Grafu ya f (x) = (x ^ 2-1)/(x ^ 2-2x-3) na asymptote yake ya wima saa x=3 na kuacha kutolewa kwa x=-1. — Kielelezo$\PageIndex{11}$.

DISCONTINUITIES INAYOONDOLEWA YA KAZI

Kuondolewa kutolewa hutokea katika grafu ya kazi ya busara$x=a$ ikiwa$a$ ni sifuri kwa sababu katika denominator ambayo ni ya kawaida na sababu katika nambari. Tunaweka namba na denominator na angalia mambo ya kawaida. Ikiwa tunapata chochote, tunaweka sababu ya kawaida sawa na 0 na kutatua. Hii ndio eneo la kuacha kutolewa. Hii ni kweli kama msururu wa jambo hili ni mkubwa kuliko au sawa na ule katika denominator. Ikiwa wingi wa jambo hili ni mkubwa zaidi katika denominator, basi bado kuna asymptote kwa thamani hiyo.

Mfano$\PageIndex{6}$: Identifying Vertical Asymptotes and Removable Discontinuities for a Graph

Kupata asymptotes wima na discontinuities kutolewa ya grafu ya$k(x)=\dfrac{x−2}{x^2−4}$.

Suluhisho

Fanya namba na denominator.

\[k(x)=\dfrac{x−2}{(x−2)(x+2)} \nonumber \]

Angalia kwamba kuna jambo la kawaida katika nambari na denominator,$x–2$. Zero kwa sababu hii ni$x=2$. Hii ndio eneo la kuacha kutolewa.

Angalia kwamba kuna sababu katika denominator ambayo si katika nambari,$x+2$. Zero kwa sababu hii ni$x=−2$. Asymptote ya wima ni$x=−2$. Angalia Kielelezo$\PageIndex{12}$.

Grafu ya k (x) = (x-2)/(x-2) (x+2) na asymptote yake ya wima saa x=-2 na kuacha kutolewa kwa x=2. — Kielelezo$\PageIndex{12}$.

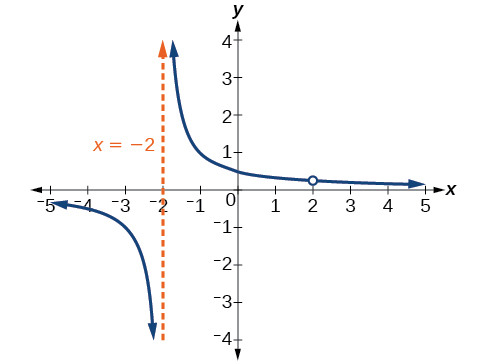
Grafu ya kazi hii itakuwa na asymptote ya wima$x=−2$, lakini$x=2$ kwenye grafu itakuwa na shimo.

Zoezi$\PageIndex{5}$

Kupata asymptotes wima na discontinuities kutolewa ya grafu ya$f(x)=\dfrac{x^2−25}{x^3−6x^2+5x}$.

Jibu

Kuondolewa kutolewa katika$x=5$.

Asymptotes ya wima:$x=0$,$x=1$.

Kutambua Asymptotes Horizontal ya Kazi za busara

Wakati asymptots wima kuelezea tabia ya grafu kama pato anapata kubwa sana au ndogo sana, asymptots usawa kusaidia kuelezea tabia ya grafu kama pembejeo anapata kubwa sana au ndogo sana. Kumbuka kwamba tabia ya mwisho ya polynomial itaonyesha ile ya neno linaloongoza. Vivyo hivyo, tabia ya mwisho ya kazi ya busara itakuwa kioo ile ya uwiano wa kazi ambayo ni uwiano wa maneno ya kuongoza.

Kuna matokeo matatu tofauti wakati wa kuangalia kwa asymptotes usawa:

Uchunguzi 1: Ikiwa kiwango cha denominator> shahada ya nambari, kuna asymptote ya usawa$y=0$.

Mfano:$f(x)=\dfrac{4x+2}{x^2+4x−5}$

Katika kesi hii, tabia ya mwisho ni$f(x)≈\dfrac{4x}{x^2}=\dfrac{4}{x}$. Hii inatuambia kwamba, kama pembejeo zinaongezeka au kupungua bila kufungwa, kazi hii itaishi sawa na kazi$g(x)=\dfrac{4}{x}$, na matokeo yatakaribia sifuri, na kusababisha asymptote ya usawa$y=0$. Angalia Kielelezo$\PageIndex{13}$. Kumbuka kwamba grafu hii inavuka asymptote ya usawa.

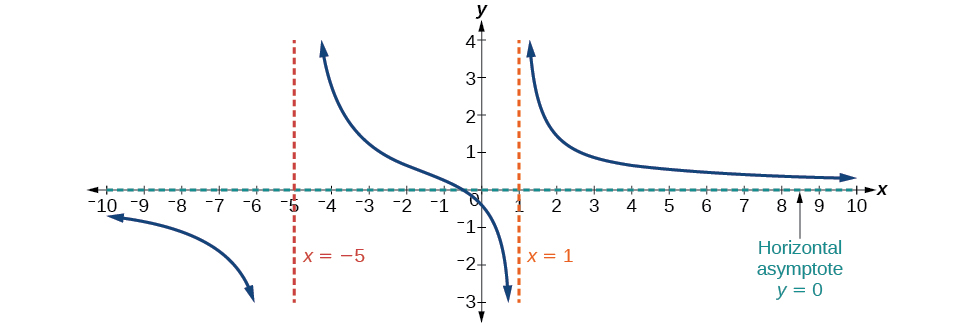
Grafu ya f (x) = (4x+2)/(x ^ 2+4x-5) na asymptots yake ya wima saa x=-5 na x=1 na asymptote yake ya usawa katika y=0. — Kielelezo$\PageIndex{13}$: Horizontal asymptote$y=0$ wakati$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$ ambapo shahada ya$p$ <shahada ya$q$.

Uchunguzi wa 2: Ikiwa kiwango cha denominator <shahada ya nambari kwa moja, tunapata asymptote ya slant.

Mfano:$f(x)=\dfrac{3x^2−2x+1}{x−1}$

Katika kesi hii, tabia ya mwisho ni$f(x)≈\dfrac{3x^2}{x}=3x$. Hii inatuambia kwamba kama pembejeo kuongezeka au kupungua bila amefungwa, kazi hii kuishi sawa na kazi$g(x)=3x$. Kama pembejeo zinakua kubwa, matokeo yatakua na sio kiwango cha mbali, hivyo grafu hii haina asymptote ya usawa. Hata hivyo, grafu ya$g(x)=3x$ inaonekana kama mstari wa diagonal, na tangu$f$ itaishi sawa na$g$, itakaribia mstari karibu na$y=3x$. Mstari huu ni asymptote ya slant.

Ili kupata equation ya asymptote ya slant, ugawanye$\dfrac{3x^2−2x+1}{x−1}$. Quotient ni$3x+1$, na salio ni 2. Asymptote ya slant ni grafu ya mstari$g(x)=3x+1$. Angalia Kielelezo$\PageIndex{14}$.

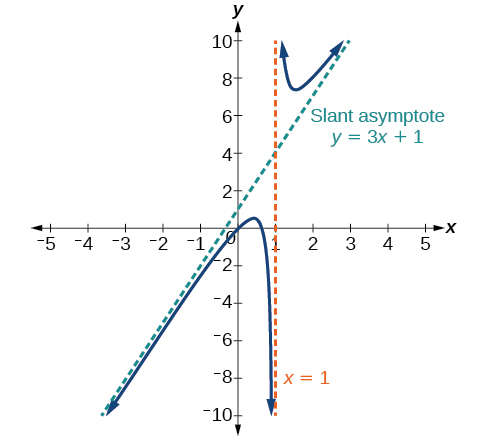
Grafu ya f (x) = (3x ^ 2-2x+1)/(x-1) na asymptote yake ya wima saa x=1 na asymptote ya slant aty=3x+1. — Kielelezo$\PageIndex{14}$: Slant asymptote wakati$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$ ambapo shahada$p$ ya> shahada ya$q$ na 1.

Uchunguzi 3: Ikiwa kiwango cha denominator = shahada ya nambari, kuna asymptote ya usawa$y=\dfrac{a_n}{b_n}$, wapi$a_n$ na$b_n$ kwa mtiririko huo coefficients inayoongoza$p(x)$ na$q(x)$ kwa$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$.

Mfano:$f(x)=\dfrac{3x^2+2}{x^2+4x−5}$

Katika kesi hii, tabia ya mwisho ni$f(x)≈\dfrac{3x^2}{x^2}=3$. Hii inatuambia kwamba kama pembejeo kukua kubwa, kazi hii itakuwa kuishi kama kazi$g(x)=3$, ambayo ni mstari usawa. Kama$x\rightarrow \pm \infty$,$f(x)\rightarrow 3$, kusababisha asymptote usawa saa$y=3$. Angalia Kielelezo$\PageIndex{15}$. Kumbuka kwamba grafu hii inavuka asymptote ya usawa.

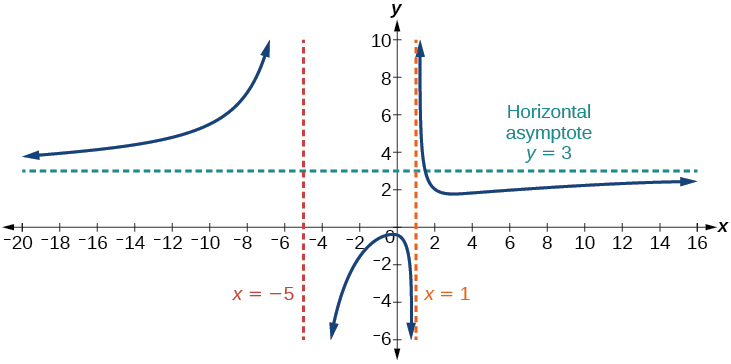
Grafu ya f (x) = (3x ^ 2+2)/(x ^ 2+4x-5) na asymptots yake ya wima saa x=-5 na x=1 na asymptote yake ya usawa katika y=3. — Kielelezo$\PageIndex{15}$: Horizontal asymptote wakati$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$ ambapo shahada ya$p$ = shahada ya$q$.

Kumbuka kwamba, wakati grafu ya kazi ya busara haitavuka kamwe asymptote ya wima, grafu inaweza au haiwezi kuvuka asymptote ya usawa au ya slant. Pia, ingawa grafu ya kazi ya busara inaweza kuwa na asymptotes nyingi za wima, grafu itakuwa na moja zaidi ya usawa (au slant) asymptote.

Ikumbukwe kwamba, ikiwa kiwango cha nambari ni kubwa kuliko kiwango cha denominator kwa zaidi ya moja, tabia ya mwisho ya grafu itaiga tabia ya sehemu ya mwisho ya tabia. Kwa mfano, kama tulikuwa na kazi

\[f(x)=\dfrac{3x^5−x^2}{x+3} \nonumber \]

na tabia ya mwisho

\[f(x)≈\dfrac{3x^5}{x}=3x^4 \nonumber \]

tabia ya mwisho ya grafu itaonekana sawa na ile ya hata polynomial na mgawo mzuri wa kuongoza.

$x\rightarrow \pm \infty, f(x)\rightarrow \infty$

DALILI ZA USAWA ZA KAZI ZA BUSARA

Asymptote ya usawa ya kazi ya busara inaweza kuamua kwa kuangalia digrii za nambari na denominator.

Shahada ya nambari ni chini ya shahada ya denominator: asymptote ya usawa saa$y=0$.
Kiwango cha nambari ni kubwa kuliko kiwango cha denominator kwa moja: hakuna asymptote ya usawa; asymptote ya slant.
Kiwango cha nambari ni sawa na kiwango cha denominator: asymptote ya usawa kwa uwiano wa coefficients inayoongoza.

Mfano$\PageIndex{7}$: Identifying Horizontal and Slant Asymptotes

Kwa kazi zilizoorodheshwa, tambua asymptote ya usawa au ya slant.

$g(x)=\dfrac{6x^3−10x}{2x^3+5x^2}$
$h(x)=\dfrac{x^2−4x+1}{x+2}$
$k(x)=\dfrac{x^2+4x}{x^3−8}$

Suluhisho

Kwa ufumbuzi huu, tutatumia$f(x)=\dfrac{p(x)}{q(x)},\space q(x)≠0$.

$g(x)=\dfrac{6x^3−10x}{2x^3+5x^2}$: Kiwango cha$p = $ shahada ya$q=3$, hivyo tunaweza kupata asymptote ya usawa kwa kuchukua uwiano wa maneno ya kuongoza. Kuna asymptote ya usawa$y =\frac{6}{2}$ au$y=3$.
$h(x)=\dfrac{x^2−4x+1}{x+2}$: shahada ya$p=2$ na shahada ya$q=1$. Tangu$p>q$ kwa 1, kuna asymptote ya slant iliyopatikana$\dfrac{x^2−4x+1}{x+2}$.
$clipboard_e5ff4f00a1466e92caa3ddac0dac32f5b.png$
$k(x)=\dfrac{x^2+4x}{x^3−8}$: Kiwango cha$p=2$ <shahada ya$q=3$, hivyo kuna asymptote ya usawa$y=0$.

Mfano$\PageIndex{8}$ Identifying Horizontal Asymptotes

Katika tatizo la ukolezi wa sukari mapema, tuliunda equation$C(t)=\dfrac{5+t}{100+10t}$.

Pata asymptote ya usawa na uifasiri kwa muktadha wa tatizo.

Suluhisho

Nambari zote na denominator ni linear (shahada 1). Kwa sababu digrii ni sawa, kutakuwa na asymptote ya usawa katika uwiano wa coefficients inayoongoza. Katika nambari, neno la kuongoza ni$t$, na mgawo wa 1. Katika denominator, neno la kuongoza ni 10t, na mgawo wa 10. Asymptote ya usawa itakuwa katika uwiano wa maadili haya:

$t\rightarrow \infty,\space C(t)\rightarrow \frac{1}{10}$

Kazi hii itakuwa na asymptote ya usawa$y=\frac{1}{10}$.

Hii inatuambia kwamba kama maadili ya$t$ ongezeko, maadili ya$C$ mapenzi yanakaribia$\frac{1}{10}$. Katika muktadha, hii inamaanisha kwamba, kama muda mwingi unavyoendelea, ukolezi wa sukari katika tangi utakaribia moja ya kumi ya pauni ya sukari kwa kila lita ya maji au$\frac{1}{10}$ paundi kwa kila lita.

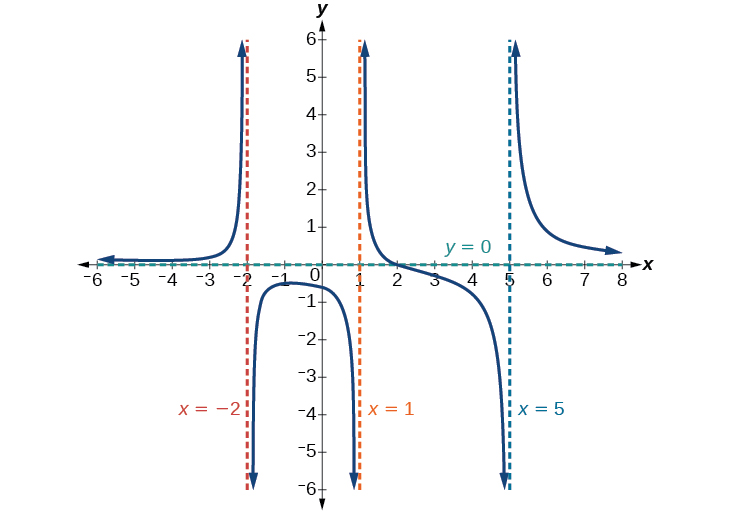
Mfano$\PageIndex{9}$: Identifying Horizontal and Vertical Asymptotes

Pata asymptotes ya usawa na wima ya kazi$f(x)=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}$

Suluhisho

Kwanza, kumbuka kuwa kazi hii haina mambo ya kawaida, kwa hiyo hakuna discontinuities zinazoweza kutolewa.

Kazi itakuwa na asymptotes wima wakati denominator ni sifuri, na kusababisha kazi kuwa haijulikani. Denominator itakuwa sifuri saa$x=1,–2,$ na$5$, kuonyesha asymptotes wima katika maadili haya.

Nambari ina shahada$2$, wakati denominator ina shahada ya 3. Kwa kuwa shahada ya denominator ni kubwa kuliko kiwango cha nambari, denominator itakua kwa kasi zaidi kuliko nambari, na kusababisha matokeo kuwa yanaelekea sifuri kama pembejeo zinapata kubwa, na hivyo$x\rightarrow \pm \infty$,$f(x)\rightarrow 0$. Kazi hii itakuwa na asymptote usawa katika$y =0.$ Angalia Kielelezo$\PageIndex{16}$.

Grafu ya f (x) = (x-2) (x+3)/(x-1) (x+2) (x-5) na asymptots zake za wima katika x=-2, x=1, na x=5 na asymptote yake ya usawa katika y=0. — Kielelezo$\PageIndex{16}$.

Zoezi$\PageIndex{6}$

Pata asymptotes ya wima na ya usawa ya kazi:

$f(x)=\dfrac{(2x−1)(2x+1)}{(x−2)(x+3)}$

Jibu

Asymptotes ya wima saa$x=2$ na$x=–3$

asymptote usawa katika$y =4$.

INACHUKUA KAZI ZA BUSARA

Kazi ya busara itakuwa na$y$ -intercept$f(0),$ ikiwa kazi inaelezwa kwa sifuri. Kazi ya busara haitakuwa na$y$ -intercept ikiwa kazi haijafafanuliwa kwenye sifuri.

Vivyo hivyo, kazi ya busara itakuwa na$x$ -intercepts katika pembejeo kwamba kusababisha pato kuwa sifuri. Kwa kuwa sehemu ni sawa na sifuri wakati namba ni sifuri, x-intercepts inaweza kutokea tu wakati nambari ya kazi ya busara ni sawa na sifuri.

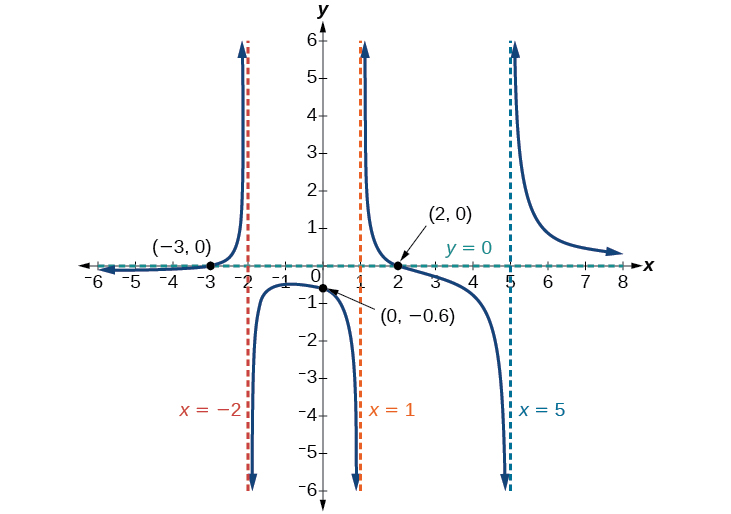
Mfano$\PageIndex{10}$: Finding the Intercepts of a Rational Function

Kupata intercepts ya $f(x)=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}$.

Suluhisho

Tunaweza kupata y-intercept kwa kutathmini kazi katika sifuri

$f(0)=\dfrac{(0−2)(0+3)}{(0−1)(0+2)(0−5)}$

$=−\dfrac{6}{10}$

$=−\dfrac{3}{5}$

$=−0.6$

X-intercepts itatokea wakati kazi ni sawa na sifuri:

\[ 0=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)} \text{ This is zero when the numerator is zero.} \nonumber \]

\[ 0=(x−2)(x+3) \qquad \qquad \qquad \qquad \qquad \nonumber \]

\[ x=2, x=−3 \qquad \qquad \qquad \qquad \qquad \nonumber \]

Y-intercept ni$(0,–0.6)$, x-intercepts ni$(2,0)$ na$(–3,0)$. Angalia Kielelezo$\PageIndex{17}$.

Grafu ya f (x) = (x-2) (x+3)/(x-1) (x+2) (x-5) na asymptots zake za wima katika x=-2, x=1, na x=5, asymptote yake ya usawa katika y = 0, na inachukua yake katika (-3, 0), (0, -0.6), na (2, 0). — Kielelezo$\PageIndex{17}$.

Zoezi$\PageIndex{7}$

Kutokana na kazi ya mraba ya usawa ambayo imebadilishwa vitengo 3 na chini ya vitengo 4, andika hii kama kazi ya busara. Kisha, tafuta x- na y-intercepts na asymptotes usawa na wima.

Jibu

Kwa kazi ya mraba iliyobadilishwa, tunapata fomu ya busara.

$f(x)=\dfrac{1}{{(x−3)}^2}−4=\dfrac{1−4{(x−3)}^2}{{(x−3)}^2}=\dfrac{1−4(x^2−6x+9)}{(x−3)(x−3)}=\dfrac{−4x^2+24x−35}{x^2−6x+9}$

Kwa sababu namba ni shahada sawa na denominator tunajua kwamba kama$x\rightarrow \pm \infty$,$f(x)\rightarrow −4$; hivyo$y=–4$ ni asymptote usawa. Kisha, tunaweka denominator sawa na sifuri, na kupata kwamba asymptote wima ni$x=3$, kwa sababu kama$x\rightarrow 3$,$f(x)\rightarrow \infty$. Sisi kisha kuweka nambari sawa$0$ na na kupata x-intercepts ni saa$(2.5,0)$ na$(3.5,0)$. Hatimaye, sisi kutathmini kazi katika 0 na kupata y-intercept kuwa katika$(0,−\frac{35}{9})$.

Graphing Kazi za Mantiki

Katika Mfano$\PageIndex{10}$, tunaona kwamba nambari ya kazi ya busara inaonyesha x -intercepts ya grafu, wakati denominator inaonyesha asymptotes wima ya grafu. Kama ilivyo na polynomials, sababu za nambari zinaweza kuwa na nguvu kamili zaidi kuliko moja. Kwa bahati nzuri, athari juu ya sura ya grafu katika wale intercepts ni sawa na tulivyoona na polynomials.

Asymptotes wima zinazohusiana na mambo ya denominator itakuwa kioo moja ya kazi mbili toolkit kubadilishwa. Wakati kiwango cha sababu katika denominator ni isiyo ya kawaida, tabia ya kutofautisha ni kwamba upande mmoja wa asymptote wima grafu inaelekea infinity chanya, na kwa upande mwingine grafu inaelekea infinity hasi. Angalia Kielelezo$\PageIndex{18}$.

Grafu ya y=1/x na asymptote yake ya wima katika x=0. — Kielelezo$\PageIndex{18}$.

Wakati kiwango cha sababu katika denominator ni hata, tabia ya kutofautisha ni kwamba grafu ama inaelekea infinity chanya pande zote mbili za asymptote wima au vichwa kuelekea infinity hasi pande zote mbili. Angalia Kielelezo$\PageIndex{19}$.

Grafu ya y=1/x ^ 2 na asymptote yake ya wima katika x=0. — Kielelezo$\PageIndex{19}$.

Kwa mfano, grafu ya $f(x)=\dfrac{{(x+1)}^2(x−3)}{{(x+3)}^2(x−2)}$inavyoonekana kwenye Kielelezo$\PageIndex{20}$.

Grafu ya f (x) = (x+1) ^2 (x-3)/(x+3) ^2 (x-2) na asymptots zake za wima katika x=-3 na x=2, asymptote yake ya usawa katika y=1, na inakabiliwa na (-1, 0), (0, 1/6), na (3, 0). — Kielelezo$\PageIndex{20}$.

Katika x-intercept$x=−1$ sambamba na${(x+1)}^2$ sababu ya nambari, grafu “bounces”, sambamba na hali ya quadratic ya sababu.
Katika x-intercept$x=3$ sambamba na$(x−3)$ sababu ya nambari, grafu hupita kupitia mhimili kama tunavyotarajia kutoka kwa sababu ya mstari.
Katika asymptote wima$x=−3$ sambamba na${(x+3)}^2$ sababu ya denominator, grafu inaelekea infinity chanya pande zote mbili za asymptote, sambamba na tabia ya kazi$f(x)=\dfrac{1}{x^2}$.
Katika asymptote wima$x=2$, sambamba na$(x−2)$ sababu ya denominator, grafu inaelekea infinity chanya upande wa kushoto wa asymptote na kuelekea infinity hasi upande wa kulia, sambamba na tabia ya kazi$f(x)=\dfrac{1}{x}$.

Jinsi ya: Kutokana na kazi ya busara, mchoro grafu.

Tathmini kazi saa 0 ili kupata y-intercept.
Fanya namba na denominator.
Kwa sababu katika nambari isiyo ya kawaida kwa denominator, onyesha ambapo kila sababu ya nambari ni sifuri ili kupata x-intercepts.
Pata wingi wa x-intercepts kuamua tabia ya grafu katika pointi hizo.
Kwa sababu katika denominator, angalia wingi wa zero ili kuamua tabia ya ndani. Kwa sababu hizo si za kawaida kwa nambari, tafuta asymptotes wima kwa kuweka mambo hayo sawa na sifuri na kisha kutatua.
Kwa sababu katika denominator kawaida kwa sababu katika nambari, kupata discontinuities removable kwa kuweka mambo hayo sawa na 0 na kisha kutatua.
Linganisha digrii za nambari na denominator ili kuamua asymptotes ya usawa au ya slant.
Mchoro grafu.

Mfano$\PageIndex{11}$: Graphing a Rational Function

Mchoro grafu ya$f(x)=\frac{(x+2)(x−3)}{{(x+1)}^2(x−2)}$.

Suluhisho

Tunaweza kuanza kwa kutambua kwamba kazi tayari imechukuliwa, kutuokoa hatua.

Kisha, tutapata intercepts. Kutathmini kazi katika sifuri hutoa y-intercept:

$f(0)=\dfrac{(0+2)(0−3)}{{(0+1)}^2(0−2)}=3$

Ili kupata x-intercepts, tunaamua wakati nambari ya kazi ni sifuri. Kuweka kila sababu sawa na sifuri, tunapata x-intercepts saa$x=–2$ na$x=3$. Kwa kila mmoja, tabia itakuwa mstari (wingi 1), na grafu inayopita kupitia intercept.

Tuna y-intercept katika$(0,3)$ na x-intercepts katika$(–2,0)$ na$(3,0)$.

Ili kupata asymptotes wima, tunaamua wakati denominator ni sawa na sifuri. Hii hutokea wakati$x+1=0$ na wakati$x–2=0$, kutupa asymptotes wima katika$x=–1$ na$x=2$.

Hakuna mambo ya kawaida katika nambari na denominator. Hii inamaanisha kuwa hakuna discontinuities inayoondolewa.

Hatimaye, kiwango cha denominator ni kubwa kuliko kiwango cha nambari, inatuambia grafu hii ina asymptote ya usawa$y =0$.

Kwa mchoro grafu, tunaweza kuanza kwa kupanga njama intercepts tatu. Kwa kuwa grafu haina x-intercepts kati ya asymptots wima, na y-intercept ni chanya, tunajua kazi lazima kubaki chanya kati ya asymptots, kuruhusu sisi kujaza sehemu ya kati ya grafu kama inavyoonekana katika Kielelezo$\PageIndex{21}$.

Grafu ya sehemu ya kati tu ya f (x) = (x+2) (x-3)/(x+1) ^2 (x-2) na intercepts yake katika (-2, 0), (0, 3), na (3, 0). — Kielelezo$\PageIndex{21}$.

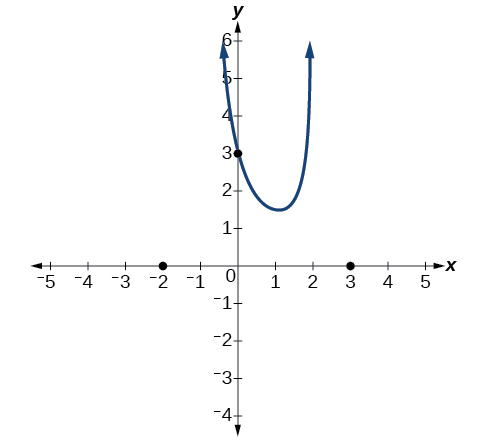
Sababu inayohusishwa na asymptote ya wima$x=−1$ ilikuwa mraba, kwa hiyo tunajua tabia itakuwa sawa pande zote mbili za asymptote. Grafu inaelekea infinity nzuri kama pembejeo inakaribia asymptote upande wa kulia, hivyo grafu itaelekea kuelekea infinity chanya upande wa kushoto pia.

Kwa asymptote wima saa$x=2$, sababu haikuwa mraba, hivyo grafu itakuwa na tabia tofauti upande wowote wa asymptote. Angalia Kielelezo$\PageIndex{22}$. Baada ya kupitisha x-intercepts, grafu hiyo itaondoka kuelekea pato la sifuri, kama ilivyoonyeshwa na asymptote ya usawa.

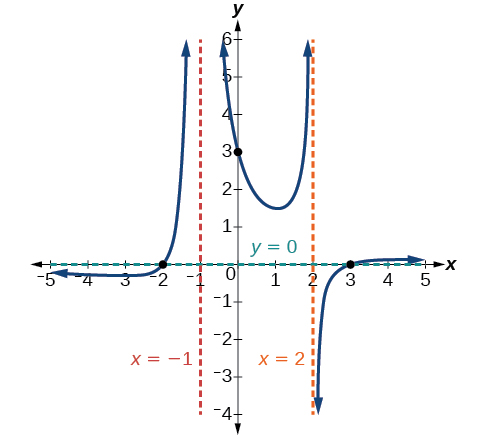
Grafu ya f (x) = (x+2) (x-3)/(x+1) ^2 (x-2) na asymptots yake ya wima katika x=-1 na x=2, asymptote yake ya usawa katika y = 0, na inachukua yake katika (-2, 0), (0, 3), na (3, 0). — Kielelezo$\PageIndex{22}$.

Zoezi$\PageIndex{8}$

Kutokana na kazi$f(x)=\frac{{(x+2)}^2(x−2)}{2{(x−1)}^2(x−3)}$, tumia sifa za polynomials na kazi za busara kuelezea tabia yake na mchoro kazi.

Jibu

Horizontal asymptote saa$y=\frac{1}{2}$. Asymptotes ya wima$x=1$ na$x=3$. y-intercept saa$(0,\frac{4}{3})$.

x-intercepts katika$(2,0)$ na$(–2,0)$. $(–2,0)$ni sifuri na wingi$2$, na grafu huondoka kwenye mhimili wa x kwa hatua hii. $(2,0)$ni sifuri moja na grafu huvuka mhimili kwa hatua hii.

Grafu ya f (x) = (x+2) ^2 (x-2) /2 (x-1) ^2 (x-3) na asymptots yake ya wima na ya usawa. — Kielelezo$\PageIndex{23}$.

Kuandika Kazi za busara

Sasa kwa kuwa tumechambua usawa wa kazi za busara na jinsi wanavyohusiana na grafu ya kazi, tunaweza kutumia habari iliyotolewa na grafu kuandika kazi. Kazi ya busara iliyoandikwa katika fomu iliyopangwa itakuwa na x -intercept ambapo kila sababu ya namba ni sawa na sifuri. (Isipokuwa hutokea katika kesi ya discontinuity removable.) Matokeo yake, tunaweza kuunda namba ya kazi ambayo grafu itapita kupitia seti ya x -intercepts kwa kuanzisha seti sambamba ya mambo. Vivyo hivyo, kwa sababu kazi itakuwa na asymptote wima ambapo kila sababu ya denominator ni sawa na sifuri, tunaweza kuunda denominator ambayo kuzalisha asymptots wima kwa kuanzisha seti sambamba ya mambo.

KUANDIKA KAZI ZA BUSARA KUTOKA KWA INTERCEPTS NA ASYMPTOTES

Ikiwa kazi ya busara ina x-intercepts saa$x=x_1,x_2,...,x_n$, asymptotes wima$x_i=$ saa$x=v_1,v_2,…,v_m$$v_j$, na hakuna, basi kazi inaweza kuandikwa kwa fomu:

$f(x)=a\dfrac{ {(x−x_1)}^{p_1} {(x−x_2)}^{p_2}⋯{(x−x_n)}^{p_n} }{ {(x−v_1)}^{q_1} {(x−v_2)}^{q_2}⋯{(x−v_m)}^{q_n}}$

ambapo nguvu$p_i$ au$q_i$ juu ya kila sababu inaweza kuamua na tabia ya grafu katika intercept sambamba au asymptote, na kunyoosha sababu$a$ inaweza kuamua kutokana na thamani ya kazi isipokuwa x-intercept au asymptote usawa kama ni nonzero.

Kutokana na grafu ya kazi ya busara, andika kazi.

Tambua sababu za nambari. Kuchunguza tabia ya grafu katika x -intercepts kuamua zero na kuzidisha yao. (Hii ni rahisi kufanya wakati wa kutafuta kazi “rahisi” na kuzidisha ndogo-kama vile 1 au 3—lakini inaweza kuwa vigumu kwa kuzidisha kubwa-kama vile 5 au 7, kwa mfano.)
Kuamua sababu za denominator. Kuchunguza tabia kwa pande zote mbili za asymptote wima kuamua sababu na nguvu zao.
Tumia hatua yoyote ya wazi kwenye grafu ili kupata sababu ya kunyoosha.

Mfano$\PageIndex{12}$: Writing a Rational Function from Intercepts and Asymptotes

Andika equation kwa kazi ya busara inavyoonekana katika Kielelezo$\PageIndex{24}$.

Grafu ya kazi ya busara. — Kielelezo$\PageIndex{24}$.

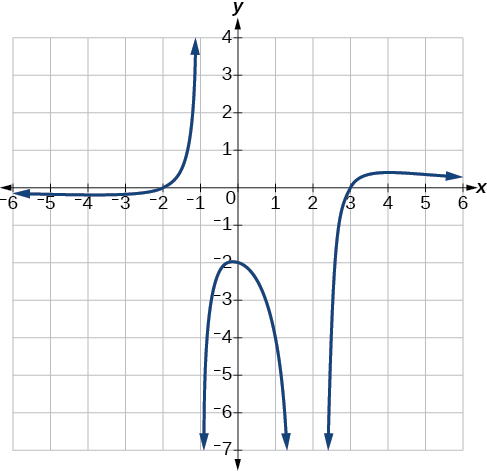
Suluhisho

Grafu inaonekana kuwa na x-intercepts saa$x=–2$ na$x=3$. Kwa wote wawili, grafu hupita kupitia intercept, na kupendekeza mambo ya mstari. Grafu ina asymptotes mbili za wima. Moja$x=–1$ inaonekana kuonyesha tabia ya msingi sawa na$\dfrac{1}{x}$, na grafu inaelekea kuelekea infinity chanya upande mmoja na kuelekea kuelekea infinity hasi kwa upande mwingine. Asymptote katika$x=2$ inaonyesha tabia sawa na$\dfrac{1}{x^2}$, na grafu inaelekea kuelekea infinity hasi pande zote mbili za asymptote. Angalia Kielelezo$\PageIndex{25}$.

Grafu ya kazi ya busara inayoashiria asymptotes yake ya wima na x-intercepts. — Kielelezo$\PageIndex{25}$.

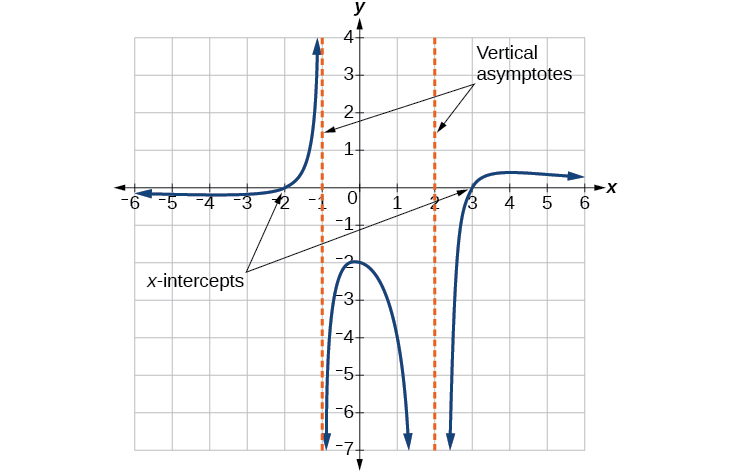
Tunaweza kutumia habari hii kuandika kazi ya fomu

$f(x)=a\dfrac{(x+2)(x−3)}{(x+1){(x−2)}^2}$

Ili kupata sababu ya kunyoosha, tunaweza kutumia hatua nyingine wazi kwenye grafu, kama vile y -intercept$(0,–2)$.

$−2=a\dfrac{(0+2)(0−3)}{(0+1){(0−2)}^2}$

$-2=a\dfrac{−6}{4}$

$a=\dfrac{−8}{−6}=\dfrac{4}{3}$

Hii inatupa kazi ya mwisho ya$f(x)=\dfrac{4(x+2)(x−3)}{3(x+1){(x−2)}^2}$.

vyombo vya habari

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kazi za busara.

Mlinganyo muhimu

Kazi ya busara$ \qquad $$f(x)=\dfrac{P(x)}{Q(x)}=\dfrac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0},\space Q(x)≠0$

Dhana muhimu

Tunaweza kutumia arrow nukuu kuelezea tabia ya ndani na tabia ya mwisho ya kazi toolkit$f(x)=\frac{1}{x}$ na$f(x)=\frac{1}{x^2}$. Angalia Mfano$\PageIndex{1}$.
Kazi ambayo inazidi kwa thamani ya usawa ina asymptote ya usawa. Kazi inaweza kuwa na asymptote zaidi ya moja ya wima. Angalia Mfano.
Matatizo ya maombi yanayohusisha viwango na viwango mara nyingi huhusisha kazi za busara. Angalia Mfano.
Kikoa cha kazi ya busara kinajumuisha namba zote halisi isipokuwa zile zinazosababisha denominator kuwa sifuri sawa. Angalia Mfano.
Asymptotes wima ya kazi ya busara itatokea ambapo denominator ya kazi ni sawa na sifuri na nambari si sifuri. Angalia Mfano.
Kuondolewa kwa kutolewa kunaweza kutokea katika grafu ya kazi ya busara ikiwa pembejeo husababisha nambari zote mbili na denominator kuwa sifuri. Angalia Mfano.
Tabia ya mwisho ya kazi ya busara itaonyesha ile ya uwiano wa maneno ya kuongoza ya kazi za nambari na denominator. Angalia Mfano, Mfano, Mfano, na Mfano.
Grafu kazi ya busara kwa kutafuta intercepts, tabia katika intercepts na asymptotes, na tabia ya mwisho. Angalia Mfano.
Ikiwa kazi ya busara ina x-intercepts saa$x=x_1,x_2,…,x_n$, asymptotes wima$x_i=$ saa$x=v_1,v_2,…,v_m$$v_j$, na hakuna, basi kazi inaweza kuandikwa kwa fomu

Mkono	Maana
\(x\rightarrow a^-\)	\(x\)inakaribia kutoka upande wa kushoto (\(x<a\)lakini karibu na\(a\))
\(x\rightarrow a^+\)	\(x\)mbinu kutoka kulia (\(x>a\)lakini karibu na\(a\))
\(x\rightarrow \infty\)	\(x\)inakaribia infinity (\(x\)huongezeka bila kufungwa)
\(x\rightarrow −\infty\)	\(x\)inakaribia infinity hasi (\(x\)itapungua bila kufungwa)
\(f(x)\rightarrow \infty\)	pato inakaribia infinity (pato huongezeka bila kufungwa)
\(f(x)\rightarrow −\infty\)	pato inakaribia infinity hasi (pato hupungua bila kufungwa)
\(f(x)\rightarrow a\)	mbinu za pato\(a\)

\(x\)	—0.1	—0.01	—0.001	— 0.0001
\(f(x)=\frac{1}{x}\)	—10	—100	—1000	—10,000

Kutumia Arrow Nukuu

Tabia ya Mitaa ya\(f(x)=\frac{1}{x}\)

Mwisho Tabia ya\(f(x)=\frac{1}{x}\)

Kutatua Matatizo yaliyotumika Kuhusisha Kazi za busara

Kutafuta Domains ya Kazi za busara

Kutambua Asymptotes ya Wima ya Kazi za Bora

Asymptotes ya wima

Discontinuities inayoondolewa

Kutambua Asymptotes Horizontal ya Kazi za busara

Graphing Kazi za Mantiki

Kuandika Kazi za busara

Mlinganyo muhimu

Dhana muhimu