3.6: Zero za Kazi za Polynomial

Malengo ya kujifunza

• Tathmini polynomial kutumia Theorem ya Salio.
• Tumia Theorem ya Factor kutatua equation ya polynomial.
• Tumia Theorem ya Zero ya Mantiki ili kupata zero za busara.
• Pata zero za kazi ya polynomial.
• Tumia Theorem ya Factorization ya Linear ili kupata polynomials na zero zilizopewa.
• Tumia Utawala wa Descartes wa Ishara.
• Tatua matumizi halisi ya ulimwengu wa milinganyo ya polynomial

Bakery mpya hutoa mikate ya karatasi iliyopambwa kwa vyama vya kuzaliwa vya watoto na matukio mengine maalum. Bakery inataka kiasi cha keki ndogo kuwa inchi 351 za ujazo. Keki iko katika sura ya imara ya mstatili. Wanataka urefu wa keki uwe mrefu wa inchi nne kuliko upana wa keki na urefu wa keki kuwa theluthi moja ya upana. Je! Vipimo vya sufuria ya keki vinapaswa kuwa nini?

Tatizo hili linaweza kutatuliwa kwa kuandika kazi ya ujazo na kutatua equation ya ujazo kwa kiasi cha keki. Katika sehemu hii, tutajadili zana mbalimbali za kuandika kazi za polynomial na kutatua usawa wa polynomial.

Kutathmini Polynomial Kutumia Theorem ya Salio

Katika sehemu ya mwisho, tulijifunza jinsi ya kugawanya polynomials. Sasa tunaweza kutumia mgawanyiko wa polynomial kutathmini polynomials kwa kutumia Theorem ya Salio. Ikiwa polynomial imegawanywa na\(x–k\), salio inaweza kupatikana haraka kwa kutathmini kazi ya polynomial saa\(k\), yaani,\(f(k)\). Hebu tembee kupitia ushahidi wa theorem.

Kumbuka kwamba Idara Algorithm inasema kwamba, kutokana\(f(x)\) na mgao polynomial na yasiyo ya sifuri polynomial mgawanyiko\(d(x)\) ambapo shahada ya\(d(x)\) ni chini ya au sawa na shahada ya\(f(x)\), kuna polynomials kipekee\(q(x)\) na\(r(x)\) vile kwamba

\[f(x)=d(x)q(x)+r(x) \nonumber\]

Kama mgawanyiko,\(d(x)\), ni\(x−k\), hii inachukua fomu

\[f(x)=(x−k)q(x)+r \nonumber\]

Tangu mgawanyiko\(x−k\)

ni linear, salio itakuwa mara kwa mara,\(r\). Na, kama sisi kutathmini hii kwa\(x=k\), tuna

\[\begin{align*} f(k)&=(k−k)q(k)+r \\[4pt] &=0{\cdot}q(k)+r \\[4pt] &=r \end{align*}\]

Kwa maneno mengine,\(f(k)\) ni salio kupatikana kwa kugawa\(f(x)\) na\(x−k\).

Theorem ya Salio

Ikiwa polynomial\(f(x)\) imegawanywa na\(x−k\), basi salio ni thamani\(f(k)\).

Kutokana na kazi ya polynomial\(f\), tathmini\(f(x)\) kwa\(x=k\) kutumia Theorem ya Salio.

1. Tumia mgawanyiko wa synthetic kugawanya polynomial na\(x−k\).
2. Salio ni thamani\(f(k)\).

Mfano\(\PageIndex{1}\): Using the Remainder Theorem to Evaluate a Polynomial

Tumia Theorem ya Salio ili kutathmini\(f(x)=6x^4−x^3−15x^2+2x−7\) saa\(x=2\).

Suluhisho

Ili kupata salio kwa kutumia Theorem ya Salio, tumia mgawanyiko wa synthetic kugawanya polynomial na\(x−2\).

\[ 2 \begin{array}{|ccccc} \; 6 & −1 & −15 & 2 & −7 \\ \text{} & 12 & 22 & 14 & 32 \\ \hline \end{array} \\ \begin{array}{ccccc} 6 & 11 & \; 7 & \;\;16 & \;\; 25 \end{array} \]

Salio ni 25. Kwa hiyo,\(f(2)=25\).

Uchambuzi

Tunaweza kuangalia jibu letu kwa kutathmini\(f(2)\).

\[\begin{align*} f(x)&=6x^4−x^3−15x^2+2x−7 \\ f(2)&=6(2)^4−(2)^3−15(2)^2+2(2)−7 \\ &=25 \end{align*}\]

Zoezi\(\PageIndex{1}\)

Tumia Theorem ya Salio ili kutathmini\(f(x)=2x^5−3x^4−9x^3+8x^2+2\) saa\(x=−3\).

Jibu

\(f(−3)=−412\)

Kutumia Theorem ya Sababu ya Kutatua Equation ya Polynomial

Theorem ya Factor ni theorem nyingine ambayo inatusaidia kuchambua equations polynomial. Inatuambia jinsi zero za polynomial zinahusiana na mambo. Kumbuka kwamba Algorithm Idara.

\[f(x)=(x−k)q(x)+r\]

Ikiwa\(k\) ni sifuri, basi salio\(r\) ni\(f(k)=0\) na\(f (x)=(x−k)q(x)+0\) au\(f(x)=(x−k)q(x)\).

Taarifa, imeandikwa katika fomu hii,\(x−k\) ni sababu ya\(f(x)\). Tunaweza kuhitimisha kama\(k\) ni sifuri ya\(f(x)\), basi\(x−k\) ni sababu ya\(f(x)\).

Vile vile, kama\(x−k\) ni sababu ya\(f(x)\), basi salio ya Algorithm Idara\(f(x)=(x−k)q(x)+r\) ni\(0\). Hii inatuambia kwamba\(k\) ni sifuri.

Hii jozi ya maana ni Theorem Factor. Kama tutakavyoona hivi karibuni, shahada ya shahada\(n\) katika mfumo wa nambari tata itakuwa na\(n\) zero. Tunaweza kutumia Theorem ya Factor ili kuzingatia kabisa polynomial katika bidhaa ya\(n\) mambo. Mara baada ya polynomial imechukuliwa kabisa, tunaweza kuamua kwa urahisi zero za polynomial.

THEOREM YA SABABU

Kwa mujibu wa Theorem Factor,\(k\) ni sifuri ya\(f(x)\) kama na tu kama\((x−k)\) ni sababu ya\(f(x)\).

Jinsi ya: Kutokana na sababu na polynomial ya shahada ya tatu, tumia Theorem ya Factor ili kuzingatia polynomial

1. Tumia mgawanyiko wa synthetic kugawanya polynomial na\((x−k)\).
2. Thibitisha kwamba salio ni\(0\).
3. Andika polynomial kama bidhaa\((x−k)\) na quotient quadratic.
4. Ikiwezekana, fikiria quadratic.
5. Andika polynomial kama bidhaa ya mambo.

Mfano\(\PageIndex{2}\): Using the Factor Theorem to Solve a Polynomial Equation

Onyesha kwamba\((x+2)\) ni sababu ya\(x^3−6x^2−x+30\). Pata mambo yaliyobaki. Tumia mambo ya kuamua zero za polynomial.

Suluhisho

Tunaweza kutumia mgawanyiko wa synthetic kuonyesha kwamba\((x+2)\) ni sababu ya polynomial.

\[ -2 \begin{array}{|cccc} \; 1 & −6 & −1 & 30 \\ \text{} & -2 & 16 & -30 \\ \hline \end{array} \\ \begin{array}{cccc} 1 & -8 & \; 15 & \;\;0 \end{array} \]

Salio ni sifuri, hivyo\((x+2)\) ni sababu ya polynomial. Tunaweza kutumia Algorithm ya Idara kuandika polynomial kama bidhaa ya mgawanyiko na quotient:

\[(x+2)(x^2−8x+15)\]

Tunaweza sababu ya quadratic kuandika polynomial kama

\[(x+2)(x−3)(x−5)\]

Kwa Theorem ya Factor, zero za\(x^3−6x^2−x+30\) ni —2, 3, na 5.

Zoezi\(\PageIndex{2}\)

Tumia Theorem ya Factor kupata zero za\(f(x)=x^3+4x^2−4x−16\) kupewa kwamba\((x−2)\) ni sababu ya polynomial.

Jibu

Zeros ni 2, —2, na —4.

Kutumia Theorem ya Zero ya Mantiki ili Kupata Zero za busara

Matumizi mengine kwa Theorem ya Salio ni kupima kama namba ya busara ni sifuri kwa polynomial iliyotolewa. Lakini kwanza tunahitaji bwawa la namba za busara kupima. Theorem ya Zero ya Mantiki inatusaidia kupunguza idadi ya zero zinazowezekana za busara kwa kutumia uwiano wa sababu za muda wa mara kwa mara na sababu za mgawo wa kuongoza wa polynomial

Fikiria kazi ya quadratic na zero mbili,\(x=\frac{2}{5}\) na\(x=\frac{3}{4}\). Kwa Theorem ya Factor, zero hizi zina sababu zinazohusiana nao. Hebu tuweke kila sababu sawa na 0, na kisha tengeneze kazi ya awali ya quadratic mbali na sababu yake ya kuenea.

Angalia kwamba mambo mawili ya muda wa mara kwa mara, 6, ni namba mbili kutoka mizizi ya awali ya busara: 2 na 3. Vile vile, sababu mbili kutoka kwa mgawo wa kuongoza, 20, ni denominators mbili kutoka mizizi ya awali ya busara: 5 na 4.

Tunaweza kudai kwamba nambari za mizizi ya busara zitakuwa daima sababu za muda wa mara kwa mara na denominators itakuwa sababu za mgawo wa kuongoza. Hii ni kiini cha Theorem ya Zero ya Mantiki; ni njia ya kutupa bwawa la zero zinazowezekana.

THEOREM YA SIFURI YA BUS

Theorem ya Zero ya Mantiki inasema kwamba, ikiwa polynomial\(f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0\) ina coefficients integer, basi kila sifuri ya busara ya\(f(x)\) ina fomu\(\frac{p}{q}\) ambapo\(p\) ni sababu ya muda wa mara kwa mara\(a_0\) na\(q\) ni sababu ya mgawo wa kuongoza\(a_n\).

Wakati mgawo wa kuongoza ni 1, zero zinazowezekana za busara ni sababu za muda wa mara kwa mara.

Jinsi ya: Kutokana na kazi ya polynomial\(f(x)\), use the Rational Zero Theorem to find rational zeros.

1. Kuamua mambo yote ya muda wa mara kwa mara na mambo yote ya mgawo wa kuongoza.
2. Kuamua maadili yote iwezekanavyo ya\(\dfrac{p}{q}\), ambapo\(p\) ni sababu ya muda wa mara kwa mara na\(q\) ni sababu ya mgawo wa kuongoza. Kuwa na uhakika wa ni pamoja na wagombea wote chanya na hasi.
3. Kuamua ambayo zeros iwezekanavyo ni zero halisi kwa kutathmini kila kesi ya\(f(\frac{p}{q})\).

Mfano\(\PageIndex{3}\): Listing All Possible Rational Zeros

Orodha zote inawezekana zeros busara ya\(f(x)=2x^4−5x^3+x^2−4\).

Suluhisho

Zero pekee zinazowezekana za busara\(f(x)\) ni quotients ya sababu za muda wa mwisho, -4, na sababu za mgawo wa kuongoza, 2.

Neno la mara kwa mara ni —4; sababu za —4 ni\(p=±1,±2,±4\).

Mgawo wa kuongoza ni 2; sababu za 2 ni\(q=±1,±2\).

Ikiwa mojawapo ya zero nne halisi ni zero za busara, basi watakuwa wa moja ya mambo yafuatayo ya -4 imegawanywa na moja ya sababu za 2.

\[\dfrac{p}{q}=±\dfrac{1}{1},±\dfrac{1}{2} \; \; \; \; \; \; \frac{p}{q}=±\dfrac{2}{1},±\dfrac{2}{2} \; \; \; \; \; \; \dfrac{p}{q}=±\dfrac{4}{1},±\dfrac{4}{2} \nonumber\]

Kumbuka kwamba\(\frac{2}{2}=1\) na\(\frac{4}{2}=2\), ambayo tayari imeorodheshwa. Hivyo tunaweza kufupisha orodha yetu.

\[\dfrac{p}{q} = \dfrac{\text{Factors of the last}}{\text{Factors of the first}}=±1,±2,±4,±\dfrac{1}{2}\nonumber \]

Mfano\(\PageIndex{4}\): Using the Rational Zero Theorem to Find Rational Zeros

Tumia Theorem ya Zero ya Mantiki ili kupata zero za busara za\(f(x)=2x^3+x^2−4x+1\).

Suluhisho

Theorem ya Zero ya Mantiki inatuambia kwamba ikiwa\(\frac{p}{q}\)\(p\) ni sifuri ya\(f(x)\), basi ni sababu ya 1 na\(q\) ni sababu ya 2.

\[ \begin{align*} \dfrac{p}{q}=\dfrac{factor\space of\space constant\space term}{factor\space of\space leading\space coefficient} \\[4pt] &=\dfrac{factor\space of\space 1}{factor\space of\space 2} \end{align*}\]

Sababu za 1 ni ± 1 na sababu za 2 ni ± 1 na ± 2. maadili inawezekana kwa\(\frac{p}{q}\) ni ± 1 na\(±\frac{1}{2}\). Hizi ni zero za busara zinazowezekana kwa kazi. Tunaweza kuamua ni ipi kati ya zeros iwezekanavyo ni zeros halisi kwa kubadilisha maadili haya kwa\(x\) in\(f(x)\).

\[f(−1)=2{(−1)}^3+{(−1)}^2−4(−1)+1=4\]

\[f(1)=1{(1)}^3+{(1)}^2−4(1)+1=0\]

\[f(−\dfrac{1}{2})=2{(−\dfrac{1}{2})}^3+{(−\dfrac{1}{2})}^2−4(−\dfrac{1}{2})+1=3\]

\[f(\dfrac{1}{2})=2{(\dfrac{1}{2})}^3+{(\dfrac{1}{2})}^2−4(\dfrac{1}{2})+1=−\dfrac{1}{2}\]

Kati ya wale\(−1\),\(−\dfrac{1}{2}\),, na si\(\dfrac{1}{2}\) zeros ya\(f(x)\). 1 ni tu busara sifuri ya\(f(x)\).

Zoezi\(\PageIndex{3}\)

Tumia Theorem ya Zero ya Mantiki ili kupata zero za busara za\(f(x)=x^3−5x^2+2x+1\).

Jibu

Hakuna zero za busara.

Kutafuta Zero za Kazi za Polynomial

Theorem ya Zero ya Mantiki inatusaidia kupunguza orodha ya zero zinazowezekana za busara kwa kazi ya polynomial. Mara baada ya kufanya hivyo, tunaweza kutumia mgawanyiko wa synthetic mara kwa mara ili kuamua zero zote za kazi ya polynomial.

Jinsi ya: Kutokana na kazi ya polynomial\(f\), use synthetic division to find its zeros.

1. Tumia Theorem ya Zero ya Mantiki ili kuorodhesha zero zote zinazowezekana za kazi.
2. Tumia mgawanyiko wa synthetic kutathmini sifuri inayowezekana kwa kugawanya mgombea katika polynomial. Kama salio ni 0, mgombea ni sifuri. Kama salio si sifuri, kumtupa mgombea.
3. Kurudia hatua mbili kwa kutumia quotient kupatikana kwa mgawanyiko synthetic. Ikiwezekana, endelea mpaka quotient ni quadratic.
4. Pata zero za kazi ya quadratic. Mbinu mbili zinazowezekana za kutatua quadratics ni factoring na kutumia formula quadratic.

Mfano\(\PageIndex{5}\): Finding the Zeros of a Polynomial Function with Repeated Real Zeros

Kupata zeros ya\(f(x)=4x^3−3x−1\).

Suluhisho

Mantiki Zero Theorem inatuambia kwamba kama\(\dfrac{p}{q}\)\(p\) ni sifuri ya\(f(x)\), basi ni sababu ya -1 na\(q\) ni sababu ya 4.

\[\begin{align*}\dfrac{p}{q}=\dfrac{factor\space of\space constant\space term}{factor\space of\space leading\space coefficient} \\[4pt] =\dfrac{factor\space of\space -1}{factor\space of\space 4} \end{align*}\]

Sababu za —1 ni ± 1 na mambo ya 4 ni ± 1, ± 2, na ± 4. Maadili iwezekanavyo\(\dfrac{p}{q}\) ni\(±1\),\(±\dfrac{1}{2}\), na\(±\dfrac{1}{4}\). Hizi ni zero za busara zinazowezekana kwa kazi. Tutatumia mgawanyiko wa synthetic kutathmini kila sifuri iwezekanavyo mpaka tutapata moja ambayo inatoa salio ya 0. Hebu tuanze na 1.

Kugawanyika kwa\((x−1)\) anatoa salio ya 0, hivyo 1 ni sifuri ya kazi. Polynomial inaweza kuandikwa kama

\[(x−1)(4x^2+4x+1) \nonumber\]

Quadratic ni mraba kamilifu. \(f(x)\)inaweza kuandikwa kama

\[(x−1){(2x+1)}^2\nonumber\]

Tayari tunajua kwamba 1 ni sifuri. Zero nyingine itakuwa na wingi wa 2 kwa sababu sababu ni mraba. Ili kupata zero nyingine, tunaweza kuweka sababu sawa na 0.

\[ \begin{align*} 2x+1=0 \\[4pt] x &=−\dfrac{1}{2} \end{align*}\]

Zero za kazi ni 1\(−\frac{1}{2}\) na kwa wingi 2.

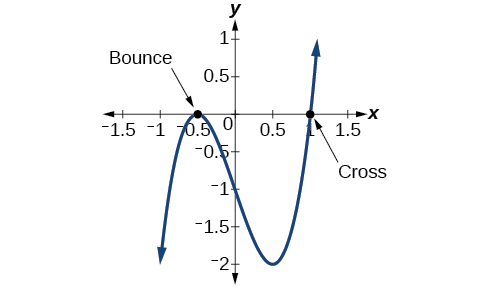
Uchambuzi

Angalia grafu ya kazi\(f\) katika Kielelezo\(\PageIndex{1}\). Angalia, saa\(x =−0.5\), grafu inaondoka kwenye mhimili wa x-axis, ikionyesha hata wingi (2,4,6...) kwa sifuri -0.5. Kwa\(x=1\), grafu inavuka mstari wa x-axis, ikionyesha wingi usio wa kawaida (1,3,5...) kwa sifuri\(x=1\).

Kielelezo\(\PageIndex{1}\).

Kutumia Theorem ya Msingi ya Algebra

Sasa kwa kuwa tunaweza kupata zero za busara kwa kazi ya polynomial, tutaangalia theorem inayozungumzia idadi ya zero tata za kazi ya polynomial. Theorem ya Msingi ya Algebra inatuambia kwamba kila kazi ya polynomial ina angalau sifuri moja tata. Theorem hii inaunda msingi wa kutatua equations polynomial.

Tuseme\(f\) ni kazi ya polynomial ya shahada nne, na\(f (x)=0\). Theorem ya Msingi ya Algebra inasema kuwa kuna angalau suluhisho moja tata, piga simu\(c_1\). Kwa Theorem ya Factor, tunaweza kuandika\(f(x)\) kama bidhaa\(x−c_1\) na quotient polynomial. Kwa kuwa\(x−c_1\) ni mstari, quotient ya polynomial itakuwa ya shahada tatu. Sasa tunatumia Theorem ya Msingi ya Algebra kwa quotient ya shahada ya tatu ya polynomial. Itakuwa na angalau sifuri moja tata, piga simu\(c_2\). Hivyo tunaweza kuandika quotient polynomial kama bidhaa ya\(x−c_2\) na mpya polynomial quotient ya shahada mbili. Endelea kutumia Theorem ya Msingi ya Algebra mpaka zero zote zinapatikana. Kutakuwa na nne kati yao na kila mmoja atatoa sababu ya\(f(x)\).

THEOREM YA MSINGI YA ALGEBRA

Theorem ya Msingi ya Algebra inasema kwamba, ikiwa\(f(x)\) ni polynomial ya shahada\(n > 0\), basi\(f(x)\) ina angalau sifuri moja tata.

Tunaweza kutumia theorem hii kusema kwamba, ikiwa\(f(x)\) ni polynomial ya shahada\(n >0\), na ni nambari isiyo ya sifuri halisi, basi\(f(x)\) ina mambo halisi ya\(n\) mstari

\[f(x)=a(x−c_1)(x−c_2)...(x−c_n)\]

ambapo\(c_1,c_2\),... ,\(c_n\) ni namba tata. Kwa hiyo,\(f(x)\) ina\(n\) mizizi ikiwa tunaruhusu kuzidisha.

Q & A: Je, kila polynomial ina angalau sifuri moja imaginary?

Hapana. Nambari halisi ni subset ya idadi tata, lakini si njia nyingine kote. Nambari ngumu sio lazima imaginary. Nambari halisi pia ni namba ngumu.

Mfano\(\PageIndex{6}\): Finding the Zeros of a Polynomial Function with Complex Zeros

Kupata zeros ya\(f(x)=3x^3+9x^2+x+3\).

Suluhisho

Theorem ya Zero ya Mantiki inatuambia kwamba ikiwa\(\frac{p}{q}\)\(p\) ni sifuri ya\(f(x)\), basi ni sababu ya 3 na\(q\) ni sababu ya 3.

\[ \begin{align*} \dfrac{p}{q}=\dfrac{factor\space of\space constant\space term}{factor\space of\space leading\space coefficient} \\[4pt] &=\dfrac{factor\space of\space 3}{factor\space of\space 3} \end{align*}\]

Sababu za 3 ni ± 1 na ± 3. maadili inawezekana kwa\(\dfrac{p}{q}\), na kwa hiyo inawezekana zeros busara kwa ajili ya kazi, ni ± 3, ± 1, na\(±\dfrac{1}{3}\). Tutatumia mgawanyiko wa synthetic kutathmini kila sifuri iwezekanavyo mpaka tutapata moja ambayo inatoa salio ya 0. Hebu tuanze na —3.

Kugawanyika kwa\((x+3)\) anatoa salio ya 0, hivyo —3 ni sifuri ya kazi. Polynomial inaweza kuandikwa kama

\[(x+3)(3x^2+1) \nonumber\]

Tunaweza kisha kuweka quadratic sawa na 0 na kutatua kupata zeros nyingine ya kazi.

\[ \begin{align*} 3x^2+1=0 \\[4pt] x^2 &=−\dfrac{1}{3} \\[4pt] x&=±−\sqrt{\dfrac{1}{3}} \\[4pt] &=±\dfrac{i\sqrt{3}}{3} \end{align*}\]

Zeros ya\(f(x)\) ni\(–3\) na\(±\dfrac{i\sqrt{3}}{3}\).

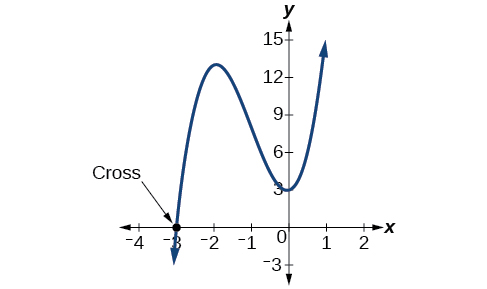
Uchambuzi

Angalia grafu ya kazi\(f\) katika Kielelezo\(\PageIndex{2}\). Angalia kwamba, saa\(x =−3\), grafu inavuka mhimili wa x-axis, ikionyesha msururu usio wa kawaida (1) kwa sifuri\(x=–3\). Pia angalia uwepo wa pointi mbili za kugeuka. Hii ina maana kwamba, kwa kuwa kuna\(3^{rd}\) shahada ya polynomial, tunaangalia idadi kubwa ya pointi za kugeuka. Hivyo, tabia ya mwisho ya kuongezeka bila kufungwa kwa haki na kupungua bila kufungwa kwa kushoto itaendelea. Hivyo, kila x-intercepts kwa ajili ya kazi ni umeonyesha. Hivyo ama msururu wa\(x=−3\) ni 1 na kuna mbili ufumbuzi tata, ambayo ni nini sisi kupatikana, au msururu katika\(x =−3\) ni tatu. Kwa njia yoyote, matokeo yetu ni sahihi.

Kielelezo\(\PageIndex{2}\).

\(\PageIndex{4}\)

Kupata zeros ya\(f(x)=2x^3+5x^2−11x+4\).

Suluhisho

Zero ni\(–4\),\(\frac{1}{2}\), na\(1\).

Kutumia Theorem ya Factorization ya Linear Kupata Polynomials na Zeros zilizopewa

Madhumuni muhimu ya Theorem ya Msingi ya Algebra, kama tulivyosema hapo juu, ni kwamba kazi ya polynomial ya shahada n itakuwa na\(n\) zero katika seti ya namba tata, ikiwa tunaruhusu kuzidisha. Hii ina maana kwamba tunaweza kuzingatia kazi ya polynomial katika\(n\) mambo. Theorem ya Factorization ya Linear inatuambia kwamba kazi ya polynomial itakuwa na idadi sawa ya mambo kama shahada yake, na kwamba kila sababu itakuwa katika fomu\((x−c)\), ambapo c ni idadi tata.

Hebu\(f\) kuwa kazi polynomial na coefficients halisi, na tuseme\(a +bi\)\(b≠0\),, ni sifuri ya\(f(x)\). Kisha, kwa Theorem Factor,\(x−(a+bi)\) ni sababu ya\(f(x)\). Kwa\(f\) kuwa na coefficients halisi,\(x−(a−bi)\) lazima pia kuwa sababu ya\(f(x)\). Hii ni kweli kwa sababu sababu yoyote isipokuwa\(x−(a−bi)\), wakati imeongezeka kwa\(x−(a+bi)\), itaacha vipengele vya kufikiri katika bidhaa. Kuzidisha tu na jozi za kuunganisha zitaondoa sehemu za kufikiri na kusababisha coefficients halisi. Kwa maneno mengine, kama kazi ya polynomial\(f\) na coefficients halisi ina sifuri tata\(a +bi\), basi conjugate tata\(a−bi\) lazima pia kuwa sifuri ya\(f(x)\). Hii inaitwa Theorem Complex Conjugate.

TATA CONJUGATE THEOREM

Kwa mujibu wa Theorem ya Factorization ya Linear, kazi ya polynomial itakuwa na idadi sawa ya mambo kama shahada yake, na kila sababu itakuwa katika fomu\((x−c)\), wapi\(c\) idadi tata.

Ikiwa kazi ya polynomial\(f\) ina coefficients halisi na sifuri tata katika fomu\(a+bi\), basi mchanganyiko tata wa sifuri\(a−bi\), pia ni sifuri.

Jinsi ya

Kutokana zero ya kazi polynomial\(f\) na uhakika\((c, f(c))\) juu ya grafu ya\(f\), kutumia Linear Factorization Theorem kupata kazi polynomial.

1. Tumia zero ili kujenga mambo ya mstari wa polynomial.
2. Panua mambo ya mstari ili kupanua polynomial.
3. \((c,f(c))\)Kuingiza katika kazi ili kuamua mgawo wa kuongoza.
4. Kurahisisha.

Mfano\(\PageIndex{7}\): Using the Linear Factorization Theorem to Find a Polynomial with Given Zeros

Pata shahada ya nne ya polynomial na coefficients halisi ambayo ina zero za\(–3\)\(2\)\(i\),, kama vile\(f(−2)=100\).

Suluhisho

Kwa sababu\(x =i\) ni sifuri, na Theorem Complex Conjugate pia\(x =–i\) ni sifuri. Polynomial lazima iwe na sababu za\((x+3),(x−2),(x−i)\), na\((x+i)\). Kwa kuwa tunatafuta shahada ya 4 polynomial, na sasa tuna zero nne, tuna mambo yote manne. Hebu tuanze kwa kuzidisha mambo haya.

\[\begin{align} f(x) & =a(x+3)(x−2)(x−i)(x+i) \\ f(x) & =a(x^2+x−6)(x^2+1) \\ f(x) & =a(x^4+x^3−5x^2+x−6) \end{align} \]

Tunahitaji kupata\(a\) ili kuhakikisha\(f(–2)=100\). Mbadala\(x=–2\) na\(f (-2)=100\) ndani ya\(f (x)\).

\[\begin{align} 100=a({(−2)}^4+{(−2)}^3−5{(−2)}^2+(−2)−6) \\ 100=a(−20) \\ −5=a \end{align} \]

Hivyo kazi ya polynomial ni

\[f(x)=−5(x^4+x^3−5x^2+x−6)\]

au

\[f(x)=−5x^4−5x^3+25x^2−5x+30\] Uchambuzi

Tuligundua kwamba wote wawili\(i\) na\(−i\) walikuwa zeros, lakini moja tu ya zero hizi zinahitajika kupewa. Ikiwa\(i\) ni sifuri ya polynomial na coefficients halisi, basi\(−i\) lazima pia kuwa sifuri ya polynomial kwa sababu\(−i\) ni conjugate tata ya\(i\).

Q & A

Ikiwa\(2+3i\) walipewa kama sifuri ya polynomial na coefficients halisi, ingehitaji\(2−3i\) pia kuwa sifuri?

Ndiyo. Wakati idadi yoyote tata na sehemu ya kufikiri inapewa kama sifuri ya polynomial na coefficients halisi, conjugate lazima pia kuwa sifuri ya polynomial.

\(\PageIndex{5}\)

Kupata shahada ya tatu polynomial na coefficients halisi ambayo ina zero ya\(5\) na\(−2i\) kama hiyo\(f (1)=10\).

Suluhisho

\(f(x)=−\frac{1}{2}x^3+\frac{5}{2}x^2−2x+10\)

Kutumia Utawala wa Descartes wa Ishara

Kuna njia moja kwa moja ya kuamua idadi iwezekanavyo ya zero halisi na hasi kwa kazi yoyote ya polynomial. Ikiwa polynomial imeandikwa kwa utaratibu wa kushuka, Utawala wa Descartes wa Ishara hutuambia uhusiano kati ya idadi ya mabadiliko ya ishara\(f(x)\) na idadi ya zero halisi. Kwa mfano, kazi ya polynomial hapa chini ina mabadiliko ya ishara moja.

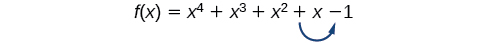
Hii inatuambia kwamba kazi lazima 1 chanya halisi sifuri.

Kuna uhusiano sawa kati ya idadi ya mabadiliko ya ishara\(f(−x)\) na idadi ya zero halisi hasi.

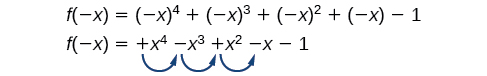
Katika kesi hii,\(f(−x)\) ina 3 mabadiliko ya ishara. Hii inatuambia kwamba\(f(x)\) inaweza kuwa na zero 3 au 1 hasi halisi.

UTAWALA WA DESCARTES WA ISHARA

Kwa mujibu wa Utawala wa Descartes wa Ishara, ikiwa tunaruhusu\(f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0\) kuwa kazi ya polynomial na coefficients halisi:

• Idadi ya zero halisi halisi ni sawa na idadi ya mabadiliko ya ishara ya\(f(x)\) au ni chini ya idadi ya mabadiliko ya ishara na hata integer.
• Idadi ya zero halisi hasi ni sawa na idadi ya mabadiliko ya ishara ya\(f(−x)\) au ni chini ya idadi ya mabadiliko ya ishara na hata integer.

Mfano\(\PageIndex{8}\): Using Descartes’ Rule of Signs

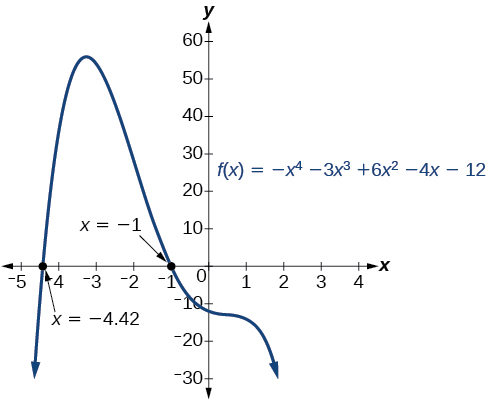
Matumizi Descartes 'Utawala wa Ishara kuamua idadi iwezekanavyo ya zero chanya na hasi halisi kwa\(f(x)=−x^4−3x^3+6x^2−4x−12\).

Suluhisho

Anza kwa kuamua idadi ya mabadiliko ya ishara.

Kuna mabadiliko mawili ya ishara, kwa hiyo kuna mizizi ya kweli ya 2 au 0. Kisha, tunachunguza\(f(−x)\) ili kuamua idadi ya mizizi halisi hasi.

\[ \begin{align} f(−x) & =−{(−x)}^4−3{(−x)}^3+6{(−x)}^2−4(−x)−12 \\ f(−x) & =−x^4+3x^3+6x^2+4x−12 \end{align} \]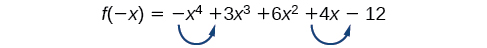

Tena, kuna mabadiliko mawili ya ishara, kwa hiyo kuna mizizi 2 au 0 hasi halisi.

Kuna uwezekano wa nne, kama tunaweza kuona katika Jedwali\(\PageIndex{1}\).

Jedwali\(\PageIndex{1}\)

Chanya Halisi Zeros	Hasi Halisi Zeros	Zeros tata	Jumla ya Zeros
2	2	0	4
2	0	2	4
0	2	2	4
0	0	4	4

Uchambuzi

Tunaweza kuthibitisha idadi ya mizizi halisi na hasi kwa kuchunguza grafu ya kazi. Angalia Kielelezo\(\PageIndex{3}\). Tunaweza kuona kutoka kwenye grafu kwamba kazi ina mizizi ya kweli ya 0 na mizizi 2 hasi halisi.

Kielelezo\(\PageIndex{3}\).

\(\PageIndex{6}\)

Matumizi Descartes 'Utawala wa Ishara kuamua idadi ya juu iwezekanavyo ya zero chanya na hasi halisi kwa\(f(x)=2x^4−10x^3+11x^2−15x+12\). Tumia grafu ili kuthibitisha idadi ya zero halisi na hasi za kazi.

Suluhisho

Lazima kuwe na mizizi 4, 2, au 0 nzuri halisi na mizizi ya kweli ya 0. Grafu inaonyesha kwamba kuna 2 zero halisi halisi na zero 0 hasi halisi.

Kutatua Matumizi halisi ya Dunia

Sasa tumeanzisha zana mbalimbali za kutatua usawa wa polynomial. Hebu tutumie zana hizi kutatua tatizo la mkate tangu mwanzo wa sehemu hiyo.

Mfano\(\PageIndex{9}\)

Kutatua equations Polynomial

Bakery mpya hutoa mikate ya karatasi iliyopambwa kwa vyama vya kuzaliwa vya watoto na matukio mengine maalum. Bakery inataka kiasi cha keki ndogo kuwa inchi 351 za ujazo. Keki iko katika sura ya imara ya mstatili. Wanataka urefu wa keki uwe mrefu wa inchi nne kuliko upana wa keki na urefu wa keki kuwa theluthi moja ya upana. Je! Vipimo vya sufuria ya keki vinapaswa kuwa nini?

Suluhisho

Anza kwa kuandika equation kwa kiasi cha keki. Kiasi cha imara ya mstatili hutolewa na\(V=lwh\). Tulipewa kwamba urefu lazima inchi nne zaidi ya upana, ili tuweze kueleza urefu wa keki kama\(l=w+4\). Tulipewa kwamba urefu wa keki ni theluthi moja ya upana, hivyo tunaweza kueleza urefu wa keki kama\(h=\dfrac{1}{3}w\). Hebu tuandike kiasi cha keki kulingana na upana wa keki.

\[V=(w+4)(w)(\dfrac{1}{3}w)\] \[V=\dfrac{1}{3}w^3+\dfrac{4}{3}w^2\]

Badilisha kiasi kilichopewa katika equation hii.

\(351=13w^3+43w^2\)Mbadala 351 kwa V. \(1053=w^3+4w^2\) kuzidisha pande zote mbili na 3. \(0=w^3+7w^2−1053\)Ondoa 1053 kutoka pande zote mbili.

Utawala wa Descartes wa ishara unatuambia kuna suluhisho moja nzuri. Theorem ya Zero ya Mantiki inatuambia kwamba zero zinazowezekana za busara ni\(\pm 1,±3,±9,±13,±27,±39,±81,±117,±351,\) na\(±1053\). Tunaweza kutumia mgawanyiko synthetic mtihani zeros hizi iwezekanavyo. Nambari nzuri tu zina maana kama vipimo vya keki, kwa hiyo hatuhitaji kupima maadili yoyote hasi. Hebu tuanze kwa kupima maadili ambayo hufanya maana zaidi kama vipimo vya keki ndogo ya karatasi. Tumia mgawanyiko wa maandishi ili\(x=1\) uangalie.

Tangu 1 sio suluhisho, tutaangalia\(x=3\).

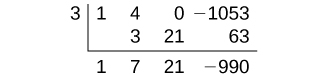
Kwa kuwa 3 sio suluhisho ama, tutajaribu\(x=9\).

Mgawanyiko wa usanifu hutoa salio la 0, hivyo 9 ni suluhisho la equation. Tunaweza kutumia mahusiano kati ya upana na vipimo vingine ili kuamua urefu na urefu wa sufuria ya keki ya karatasi.

\(l=w+4=9+4=13\)na\(h=\dfrac{1}{3}w=\dfrac{1}{3}(9)=3\)

Pani ya keki ya karatasi inapaswa kuwa na vipimo vya inchi 13 na inchi 9 na inchi 3

\(\PageIndex{7}\)

Chombo cha meli katika sura ya imara ya mstatili lazima iwe na kiasi cha mita za ujazo 84. Mteja anamwambia mtengenezaji kwamba, kwa sababu ya yaliyomo, urefu wa chombo lazima uwe mita moja zaidi kuliko upana, na urefu lazima uwe mita moja zaidi ya upana mara mbili. Vipimo vya chombo vinapaswa kuwa nini?

Suluhisho

Mita 3 na mita 4 na mita 7

Media

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na zero za kazi nyingi.

• Zero halisi, Mambo, na Grafu za Kazi za Polynomial
• Tata Factorization Theorem
• Pata Zero za Kazi ya Polynomial
• Pata Zeros ya Kazi ya Polynomial 2
• Pata Zeros ya Kazi ya Polynomial 3

Dhana muhimu

• Ili kupata\(f(k)\), tambua salio ya polynomial\(f(x)\) wakati imegawanywa na\(x−k\). Hii inajulikana kama Theorem ya Salio. Angalia Mfano\(\PageIndex{1}\).
• Kwa mujibu wa Theorem Factor,\(k\) ni sifuri ya\(f(x)\) kama na tu kama\((x−k)\) ni sababu ya\(f(x)\). Angalia Mfano\(\PageIndex{2}\).
• Kwa mujibu wa Theorem ya Zero ya Mantiki, kila sifuri ya busara ya kazi ya polynomial na coefficients integer itakuwa sawa na sababu ya muda wa mara kwa mara umegawanyika na sababu ya mgawo wa kuongoza. Angalia Mfano\(\PageIndex{3}\) na Mfano\(\PageIndex{4}\).
• Wakati mgawo wa kuongoza ni 1, zero zinazowezekana za busara ni sababu za muda wa mara kwa mara.
• Mgawanyiko wa usanifu unaweza kutumika kupata zero za kazi ya polynomial. Angalia Mfano\(\PageIndex{5}\).
• Kwa mujibu wa Theorem ya Msingi, kila kazi ya polynomial yenye shahada kubwa kuliko 0 ina angalau sifuri moja tata. Angalia Mfano\(\PageIndex{6}\).
• Kuruhusu kuzidisha, kazi ya polynomial itakuwa na idadi sawa ya mambo kama shahada yake. Kila sababu itakuwa katika fomu\((x−c)\), ambapo\(c\) ni namba tata. Angalia Mfano\(\PageIndex{7}\).
• Idadi ya zero halisi za kazi ya polynomial ni idadi ya mabadiliko ya ishara ya kazi au chini ya idadi ya ishara inabadilika na hata integer.
• Idadi ya zero halisi ya kazi ya polynomial ni ama idadi ya mabadiliko ya ishara ya\(f(−x)\) au chini ya idadi ya mabadiliko ya ishara na hata integer. Angalia Mfano\(\PageIndex{8}\).
• Ulinganyo wa polynomial mfano matukio mengi ya ulimwengu halisi. Kutatua equations ni rahisi kufanywa na mgawanyiko wa synthetic. Angalia Mfano\(\PageIndex{9}\).

faharasa

Utawala wa Descartes wa Ishara

sheria ambayo huamua idadi kubwa iwezekanavyo ya zero halisi na hasi kulingana na idadi ya mabadiliko ya ishara ya\(f(x)\) na\(f(−x)\)

Theorem ya sababu

\(k\)ni sifuri ya kazi polynomial\(f(x)\) kama na tu kama\((x−k)\) ni sababu ya\(f(x)\)

Theorem ya msingi ya Algebra

kazi ya polynomial yenye shahada kubwa kuliko 0 ina angalau sifuri moja tata

Theorem ya Kiwanda cha Mstari

kuruhusu kuzidisha, kazi ya polynomial itakuwa na idadi sawa ya mambo kama shahada yake, na kila sababu itakuwa katika fomu\((x−c)\),\(c\) wapi idadi tata

Theorem ya sifuri

zero zinazowezekana za busara za kazi ya polynomial zina fomu\(\frac{p}{q}\) ambapo\(p\) ni sababu ya muda wa mara kwa mara na\(q\) ni sababu ya mgawo wa kuongoza.

Theorem ya Salio

ikiwa polynomial\(f(x)\) imegawanywa na\(x−k\), basi salio ni sawa na thamani\(f(k)\)