3.5: Kugawanya Polynomials

Malengo ya kujifunza

• Tumia mgawanyiko mrefu kugawanya polynomials.
• Tumia mgawanyiko wa maandishi ili kugawanya polynomials.

Nje ya Lincoln Memorial katika Washington, D.C., ni kubwa mstatili imara na$61.5$ mita urefu (m), upana$40$ m, na urefu$30$ m.$^1$

Tunaweza kupata kiasi kwa urahisi kutumia jiometri ya msingi.

$$\begin{align*} V&=l \; {\cdot} \; w \; {\cdot} \; h \\ &=61.5 \; {\cdot} \; 40 \; {\cdot} \; 30 \\ &=73,800 \end{align*}$$

Hivyo kiasi ni mita$73,800$ za ujazo ($m^3$).

Kielelezo$\PageIndex{1}$: Lincoln Memorial, Washington, D.C. (mikopo: Ron Cogswell, Flickr)

Tuseme tulijua kiasi, urefu, na upana. Tunaweza kugawanya ili kupata urefu.

$$\begin{align*} h&=\dfrac{V}{l{\cdot}w} \\&=\dfrac{73,800}{61.5{\cdot}40} \\ &=30 \end{align*}$$

Kama tunaweza kuthibitisha kutoka vipimo hapo juu, urefu ni 30 m Tunaweza kutumia mbinu sawa ili kupata yoyote ya vipimo kukosa. Tunaweza pia kutumia njia sawa kama yoyote au yote ya vipimo vyenye maneno variable. Kwa mfano, tuseme kiasi cha imara ya mstatili hutolewa na polynomial$3x^4−3x^3−33x^2+54x$. Urefu wa imara hutolewa na$3x$; upana hutolewa na$x−2$.

Ili kupata urefu wa imara, tunaweza kutumia mgawanyiko wa polynomial, ambayo ni lengo la sehemu hii.

Kutumia Idara ya Muda mrefu kugawanya Polynomi

Tunajua na algorithm ya mgawanyiko wa muda mrefu kwa hesabu ya kawaida. Tunaanza kwa kugawa katika tarakimu za mgao ambao una thamani kubwa zaidi ya mahali. Tunagawanya, kuzidisha, toa, ni pamoja na tarakimu katika nafasi ya thamani ya mahali, na kurudia. Kwa mfano, hebu tugawanye 178 na 3 kwa kutumia mgawanyiko mrefu.

Njia nyingine ya kuangalia suluhisho ni kama jumla ya sehemu. Hii inapaswa kuangalia ya kawaida, kwa kuwa ni njia sawa inayotumiwa kuangalia mgawanyiko katika hesabu ya msingi.

$$\begin{align*} \text{dividend}&=(\text{divisor}{\cdot}\text{quotient})+\text{remainder} \\ 178&=(3{\cdot}59)+1 \\ &=177+1 \\ &=178\end{align*}$$

Tunaita hii Division Algorithm na kujadili ni rasmi zaidi baada ya kuangalia mfano.

Idara ya polynomials ambayo yana zaidi ya muda mmoja ina kufanana na mgawanyiko mrefu wa idadi nzima. Tunaweza kuandika mgao wa polynomial kama bidhaa ya mgawanyiko na quotient aliongeza kwa salio. Masharti ya mgawanyiko wa polynomial yanahusiana na tarakimu (na maadili ya mahali) ya mgawanyiko wa namba nzima. Njia hii inatuwezesha kugawanya polynomials mbili. Kwa mfano, ikiwa tungegawanyika$2x^3−3x^2+4x+5$ kwa$x+2$ kutumia algorithm ya mgawanyiko mrefu, ingekuwa inaonekana kama hii:

\\ zinahitaji {enclose}\ kuanza {safu} {rll}\ kubwa x+2\ enclose {longdiv} {2x ^ 3-3x^2+4x+5\ njozi {0}} &\ qquad &\ kubwa\ maandishi {Weka tatizo la mgawanyiko.}\\ [8pt]\ kubwa 2x^2
\ hnafasi {5.45em} &\ qquad &\ large2x2x2t] ^ 3\ maandishi {imegawanywa na} x\ maandishi {ni} 2x^2.\\ [-3pt]
\ kubwa x+2\ enclose { longdiv} {2x ^ 3-3x ^ 2+4x+5\ njozi {0}} &\ quad &\ [8pt]
\ kubwa 2x ^ 2\ hnafasi {5.45em} &\ qquad &\ [-3pt]
\ kubwa x+2\ enclose {longdiv} {2x ^ 3-3x ^ 2+4x+5\ Phantom {0}} &\ qq quad &\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (2x ^ 3 + 4x^ 2\ haki)}\ hnafasi {4.9em} & \ qquad &\ kubwa\ maandishi {Kuzidisha} x+2\ maandishi {na} 2x ^ 2\ maandishi {na Ondoa.}\\ [-3pt]
\ kubwa -7x ^ 2+4x\ hnafasi {2.8em} &\ qquad &\ kubwa\ maandishi {Lete chini mrefu.}\\ [8pt]

\ kubwa 2x ^ 2 - 7x\ hnafasi {2.85em\} &\ qquad &\ kubwa -7x ^ 2\ Nakala {imegawanywa na} x\ maandishi {ni} -7x.\\ [-3pt]
\ kubwa x+2\ enclose {longdiv} {2x ^ 3-3x ^ 2+4x+5\ njozi {0}} &\ qquad &\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (2x^3 + 4x^ 2\ haki)}\ hnafasi {4.9em} &\ qquad &\ [-3pt]
\ kubwa -7x ^ 2+4x\ hnafasi {2.8em} &\ quad &\ [-3pt]
\\ kubwa\ kusisitiza {-\ kushoto (-7x ^ 2 - 14x\ haki)}\ hnafasi {2.0em} &\ qquad &\ kubwa\ maandishi {Kuzidisha} x+2\ maandishi {na} -7x.\\ [-3pt]
\ kubwa 18x+5\ Phantom {0} &\ qquad &\ kubwa\ Nakala {Ondoa na kuleta muda ujao.}\\ [8pt]

\ kubwa 2x^2 - 7x+18 &\ qquad &\ kubwa 18x\ maandishi {kugawanywa na} x\ maandishi {ni} 18.\\ [-3pt]
\ kubwa x+2\ enclose {longdiv} {2x^3-3x ^ 2+4x+5\ njozi {0}} &\ qquad &\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (2x ^ 3 + 4x^ 2\ haki)}\ h nafasi {4.9em} &\ quad &\ [-3pt]
\ kubwa -7x ^ 2+4x\ hnafasi {2.8 em} &\ qquad &\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (-7x ^ 2 - 14x\ haki)}\ hnafasi {2.0em} &\ qquad &\ [-3pt]
\ kubwa 18x+\ njozi {0} 5 &\ qquad &\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (18x + 36\ haki)}\ hspace {-0.45em} &\ quad &\ kubwa\ maandishi {Kuzidisha} x+2\ maandishi {na} 18.\\ [-3pt]
\ kubwa -31 &\ qquad &\ kubwa\ maandishi {Ondoa.}\\ [8pt]
\ mwisho {safu}\ nonumber\]

Tumegundua

$$\dfrac{2x^3−3x^2+4x+5}{x+2}=2x^2−7x+18−\dfrac{31}{x+2} \nonumber$$

au

$$2x^3−3x^2+4x+5=(x+2)(2x^2−7x+18)−31 \nonumber$$

Tunaweza kutambua mgao, mgawanyiko, quotient, na salio.

Kuandika matokeo kwa namna hii unaeleza Idara ya Algorithm.

Algorithm Idara

Idara Algorithm inasema kwamba, kutokana$f(x)$ na mgao polynomial na yasiyo ya sifuri polynomial mgawanyiko$d(x)$ ambapo shahada ya$d(x)$ ni chini ya au sawa na shahada ya$f(x)$, kuna polynomials kipekee$q(x)$ na$r(x)$ vile kwamba

$$f(x)=d(x)q(x)+r(x)$$

$q(x)$ni quotient na$r(x)$ ni salio. Salio ni ama sawa na sifuri au ina shahada madhubuti chini ya$d(x)$.

Ikiwa$r(x)=0$, basi$d(x)$ hugawanya sawasawa$f(x)$. Hii ina maana kwamba, katika kesi hii, wote wawili$d(x)$ na$q(x)$ ni sababu za$f(x)$.

Kutokana na polynomial na binomial, tumia mgawanyiko mrefu kugawanya polynomial na binomial

1. Weka tatizo la mgawanyiko.
2. Kuamua muda wa kwanza wa quotient kwa kugawa muda wa kuongoza wa mgao kwa muda wa kuongoza wa mgawanyiko.
3. Panua jibu kwa mgawanyiko na uandike chini ya masharti kama hayo ya mgao.
4. Ondoa binomial ya chini kutoka binomial ya juu.
5. Kuleta chini mrefu ya mgao.
6. Kurudia hatua 2—5 mpaka kufikia muda wa mwisho wa mgao.
7. Ikiwa salio ni zisizo sifuri, onyesha kama sehemu kwa kutumia kigawanyo kama denominator.

Mfano$\PageIndex{1}$: Using Long Division to Divide a Second-Degree Polynomial

Gawanya$5x^2+3x−2$ na$x+1$.

Suluhisho

Quotient ni$5x−2$. Salio ni 0. Tunaandika matokeo kama

$$\dfrac{5x^2+3x−2}{x+1}=5x−2 \nonumber$$

au

$$5x^2+3x−2=(x+1)(5x−2) \nonumber$$

Uchambuzi

Tatizo hili mgawanyiko alikuwa salio ya 0. Hii inatuambia kwamba mgao umegawanyika sawasawa na mgawanyiko, na kwamba mgawanyiko ni sababu ya mgao.

Mfano$\PageIndex{2}$: Using Long Division to Divide a Third-Degree Polynomial

Gawanya$6x^3+11x^2−31x+15$ na$3x−2$.

Suluhisho

\ [\ zinahitaji {enclose}\ kuanza {safu} {rll}
\ kubwa 2x ^ 2 +\ njozi {0} 5x-\ njozi {0} 7 &\ qquad &\ kubwa 6x^3\ maandishi {kugawanywa na} 3x\ maandishi {ni} 2x^2.\\ [-3pt]\ kubwa 3x-2
\ enclose {longdiv} {6x ^ 3} {6x ^ 3pt] +11x ^ 2-31x+15} &\ qquad &\\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (6x^3 - 4x^2 \ kulia)}\ hnafasi {5.8em} &\ qquad &\ kubwa\ maandishi {Kuzidisha} 3x-2\ maandishi {na} 2x^2.\\ [-3pt]
\ kubwa 15x ^ 2-31x\ hnafasi {3.0em} &\ qquad &\ kubwa\ maandishi {Ondoa. Kuleta muda ujao.} 15x^2\ maandishi {imegawanywa na} 3x\ maandishi {ni} 5x.\\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (15x^2 - 10x\ kulia)}\ hnafasi {2.5em} &\ qquad &\ kubwa\ maandishi {Kuzidisha} 3x-2\ maandishi {na} 5x.\\ [-3pt]
\ kubwa -2121\ x+15\ hnafasi {0.5em} &\ quad &\ kubwa\ maandishi {Ondoa. Lete chini neno linalofuata.} -21x\ maandishi {imegawanywa na} 3x\ maandishi {ni} -7.\\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (-21x + 14\ haki)}\ hnafasi {0.1em} &\ qquad &\ kubwa\ maandishi {Kuzidisha} 3x-2\ maandishi {na} -7.\ [-3pt]
\ kubwa 1\ hnafasi {0.5em} &\ qquad &\ kubwa\ maandishi {Ondoa. Salio ni 1.}\\ [8pt]
\ mwisho {safu}\ nonumber\]

Kuna salio ya 1. Tunaweza kueleza matokeo kama:

$$\dfrac{6x^3+11x^2−31x+15}{3x−2}=2x^2+5x−7+\dfrac{1}{3x−2} \nonumber$$

Uchambuzi

Tunaweza kuangalia kazi yetu kwa kutumia Algorithm Idara ya kuandika upya suluhisho. Kisha kuzidisha.

$$(3x−2)(2x^2+5x−7)+1=6x^3+11x^2−31x+15 \nonumber$$

Angalia, kama sisi kuandika matokeo yetu,

• mgao ni$6x^3+11x^2−31x+15$
• mgawanyiko ni$3x−2$
• quotient ni$2x^2+5x−7$
• salio ni$1$

Jaribu! $\PageIndex{2}$

Gawanya$16x^3−12x^2+20x−3$ na$4x+5$.

Suluhisho

$4x^2−8x+15−\dfrac{78}{4x+5}$

Kutumia Idara ya Synthetic kugawanya Polyn

Kama tulivyoona, mgawanyiko mrefu wa polynomials unaweza kuhusisha hatua nyingi na kuwa mbaya sana. Mgawanyiko wa usanifu ni njia ya kupunguzwa ya kugawa polynomials kwa kesi maalum ya kugawa kwa sababu ya mstari ambao mgawo unaoongoza ni$1.$

Ili kuonyesha mchakato, kumbuka mfano mwanzoni mwa sehemu hiyo.

Gawanya$2x^3−3x^2+4x+5$ kwa$x+2$ kutumia algorithm ya mgawanyiko mrefu.

Fomu ya mwisho ya mchakato inaonekana kama hii:

\ [\ zinahitaji {enclose}\ kuanza {safu} {rl}\ 2x^2 kubwa - 7x+18 &\ [-3pt]
\ kubwa x+2\ enclose {longdiv} {2x^3-3x^2+4x+5\ Phantom {0}} &\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (2x^3 + 4x^ 2\ haki)}\ hnafasi {4.9em} &\ [-3pt]
\ kubwa -7x ^ 2+4x\ hnafasi {2.8em} &\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (-7x ^ 2 - 14x\ haki)}\ hnafasi {2.0em} &\ [-3pt]
\ kubwa 18x+\ njozi {0} 5 &\ [-3pt]
\ kubwa\ kusisitiza {-\ kushoto (18x + 36\ haki)}\ hnafasi {-0.45em} &\\ [-3pt]
\ kubwa -31 &\\ [8pt]
\ mwisho {safu}\ nonumber \]

Kuna mengi ya kurudia katika meza. Kama hatuwezi kuandika vigezo lakini, badala yake, line up coefficients yao katika nguzo chini ya ishara ya mgawanyiko na pia kuondoa bidhaa sehemu, tayari tuna toleo rahisi ya tatizo zima.

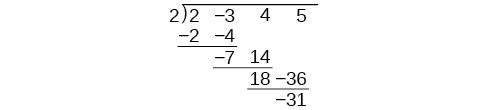
Mgawanyiko wa usanifu hubeba kurahisisha hii hata hatua chache zaidi. Kuanguka meza kwa kusonga kila safu hadi kujaza matangazo yoyote ya wazi. Pia, badala ya kugawa na 2, kama tunataka katika mgawanyiko wa idadi nzima, kisha kuzidisha na kutoa bidhaa ya kati, tunabadilisha ishara ya “mgawanyiko” hadi -2, kuzidisha na kuongeza. Utaratibu huanza kwa kuleta mgawo wa kuongoza.

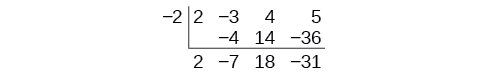
Sisi kisha kuzidisha kwa “mgawanyiko” na kuongeza, kurudia safu hii ya mchakato na safu, mpaka hakuna entries kushoto. Mstari wa chini unawakilisha coefficients ya quotient; kuingia mwisho wa mstari wa chini ni salio. Katika kesi hii, quotient ni$2x^2–7x+18$ na salio$–31.$ ni. mchakato utafanywa wazi zaidi katika Mfano$\PageIndex{3}$.

Idara ya usanifu

Mgawanyiko wa usanifu ni njia ya mkato ambayo inaweza kutumika wakati mgawanyiko ni binomial katika fomu$x−k$. Katika mgawanyiko wa synthetic, coefficients tu hutumiwa katika mchakato wa mgawanyiko.

Kutokana na polynomials mbili, tumia mgawanyiko wa synthetic kugawa

1. Andika$k$ kwa mgawanyiko.
2. Andika coefficients ya mgao.
3. Kuleta mgawo wa kuongoza chini.
4. Panua mgawo wa kuongoza na$k$. Andika bidhaa katika safu inayofuata.
5. Ongeza masharti ya safu ya pili.
6. Panua matokeo na$k$. Andika bidhaa katika safu inayofuata.
7. Kurudia hatua 5 na 6 kwa nguzo zilizobaki.
8. Tumia namba za chini kuandika quotient. Nambari katika safu ya mwisho ni salio na ina shahada ya 0, nambari inayofuata kutoka kwa haki ina shahada ya 1, namba inayofuata kutoka kwa haki ina shahada ya 2, na kadhalika.

Mfano$\PageIndex{3}$: Using Synthetic Division to Divide a Second-Degree Polynomial

Tumia mgawanyiko wa synthetic$5x^2−3x−36$ kugawa na$x−3$

Suluhisho

Anza kwa kuanzisha mgawanyiko wa synthetic. Andika$k$ na coefficients.

Kuleta mgawo wa kuongoza. Panua mgawo wa kuongoza na$k$.

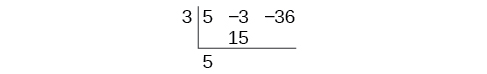
Endelea kwa kuongeza idadi katika safu ya pili. Panua nambari inayosababisha$k$ na.Andika matokeo katika safu inayofuata. Kisha kuongeza namba katika safu ya tatu.

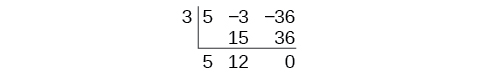
Matokeo yake ni$5x+12$. Salio ni 0. Hivyo$x−3$ ni sababu ya polynomial ya awali.

Uchambuzi

Kama ilivyo kwa mgawanyiko mrefu, tunaweza kuangalia kazi yetu kwa kuzidisha quotient na mgawanyiko na kuongeza salio.

$$(x−3)(5x+12)+0=5x^2−3x−36 \nonumber$$

Mfano$\PageIndex{4}$: Using Synthetic Division to Divide a Third-Degree Polynomial

Tumia mgawanyiko wa synthetic$4x^3+10x^2−6x−20$ kugawa na$x+2$

Suluhisho

Mgawanyiko wa binomial ni$x+2$ hivyo$k=−2$. Ongeza kila safu, kuzidisha matokeo kwa -2, na kurudia mpaka safu ya mwisho itafikia.

\ [kubwa {\ kuanza {safu} {c} -2\\\\\
\ mwisho {safu}} {\ kuanza
{align*} &\ [0pt]
& {\ kuanza {safu} {r|}\ [0pt]\
\ [0pt]\\ mwisho {safu}}\\ [1pt]
&\ [2pt] &\ mwisho {align*}}\\ \!
{\ kuanza {safu} {rrrr}
1 & -1 & -11 & 18\\
& 2 & 2 & -18\
\ hline 1 & 1 & -9 & 0
\ mwisho {safu}}
\ nonumber\]

Matokeo yake ni$4x^2+2x−10$.

Salio ni 0. Hivyo,$x+2$ ni sababu ya$4x^3+10x^2−6x−20$.

Uchambuzi

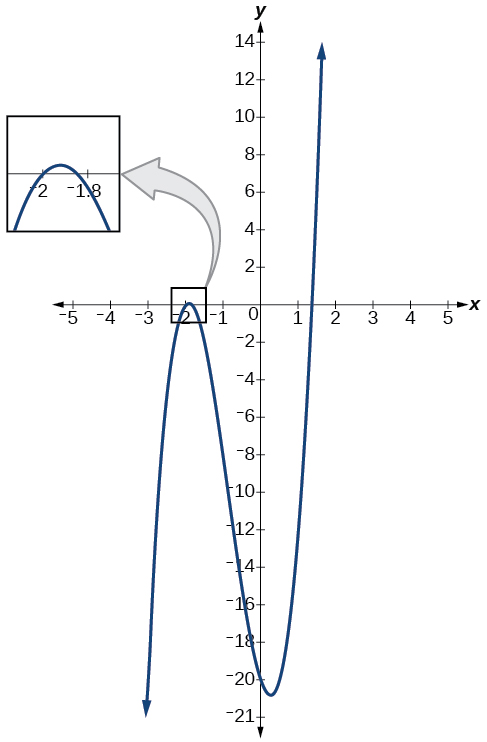
Grafu ya kazi ya polynomial$f(x)=4x^3+10x^2−6x−20$ katika Kielelezo$\PageIndex{2}$ inaonyesha sifuri saa$x=k=−2$. Hii inathibitisha kwamba$x+2$ ni sababu ya$4x^3+10x^2−6x−20$.

Kielelezo$\PageIndex{2}$

Mfano$\PageIndex{5}$: Using Synthetic Division to Divide a Fourth-Degree Polynomial

Tumia mgawanyiko wa synthetic$−9x^4+10x^3+7x^2−6$ kugawa na$x−1$

Suluhisho

Taarifa hakuna$x$ -mrefu. Tutatumia sifuri kama mgawo wa muda huo.

\ [kubwa {\ kuanza {safu} {c} 1\\\\\\
\ mwisho {safu}} {\ kuanza
{align*} &\ [0pt]
& {\ kuanza {safu} {r|}\\ [0pt]
\\ [0pt]\\ mwisho {safu}}\\ [1pt]
&\ [2pt] &\ mwisho {align*}}\\ \!
{\ kuanza {safu} {rrrr}
-9 & 10 & 7 & 0 &-6\
& -9 & 1 & 8 & 8 & 8\
\ hline -9 & 1 & 8 & 8 & 2
\ mwisho {safu}}
\ nonumber\]

Matokeo yake ni$−9x^3+x^2+8x+8+\dfrac{2}{x−1}$.

Jaribu! $\PageIndex{3}$

Tumia mgawanyiko wa synthetic$3x^4+18x^3−3x+40$ kugawa na$x+7$

Suluhisho

$3x^3−3x^2+21x−150+\dfrac{1090}{x+7}$

Kutumia Idara ya Polynomial kutatua Matatizo ya Maombi

Mgawanyiko wa polynomial unaweza kutumika kutatua matatizo mbalimbali ya maombi yanayohusisha maneno kwa eneo na kiasi. Tuliangalia programu mwanzoni mwa sehemu hii. Sasa tutasuluhisha tatizo hilo katika mfano unaofuata.

Mfano$\PageIndex{6}$: Using Polynomial Division in an Application Problem

Kiasi cha imara ya mstatili hutolewa na polynomial$3x^4−3x^3−33x^2+54x$. Urefu wa imara hutolewa$3x$ na upana hutolewa na$x−2$. Pata urefu$h$ wa imara.

Suluhisho

Kuna njia chache za kukabiliana na tatizo hili. Tunahitaji kugawanya maneno kwa kiasi cha imara kwa maneno kwa urefu na upana. Hebu kujenga mchoro kama katika Kielelezo$\PageIndex{3}$. Hebu$h$ sawa urefu wa sanduku.

Kielelezo$\PageIndex{3}$

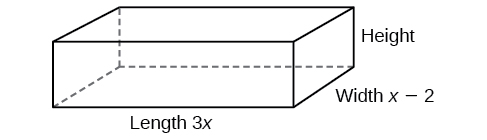
Sasa tunaweza kuandika equation kwa kubadilisha maadili inayojulikana katika formula kwa kiasi cha imara mstatili.

$$\begin{align*} V&=l{\cdot}w{\cdot}h \\ 3x^4−3x^3−33x^2+54x&=3x{\cdot}(x−2){\cdot}h \end{align*}$$

Ili kutatua$h$, kwanza ugawanye pande zote mbili na$3x$.

$$\dfrac{3x{\cdot}(x−2){\cdot}h}{3x}=\dfrac{3x^4−3x^3−33x^2+54x}{3x} \nonumber$$

$$(x-2)h=\dfrac{x^3-x^2-11x+18}{x-2} \nonumber$$

Sasa tatua kwa$h$ kutumia mgawanyiko wa maandishi.

$$h=\dfrac{x^3−x^2−11x+18}{x−2} \nonumber$$

\ [kubwa {\ kuanza {safu} {c} -2\\\\\
\ mwisho {safu}} {\ kuanza
{align*} &\ [0pt]
& {\ kuanza {safu} {r|}\ [0pt]\
\ [0pt]\\ mwisho {safu}}\\ [1pt]
&\ [2pt] &\ mwisho {align*}}\\ \!
{\ kuanza {safu} {rrrr}
1 & -1 & -11 & 18\\
& 2 & 2 & -18\
\ hline 1 & 1 & -9 & 0
\ mwisho {safu}}
\ nonumber\]

Quotient ni$x^2+x−9$ na salio ni urefu$0.$ wa imara ni$x^2+x−9$.

Jaribu! $\PageIndex{4}$

Eneo la mstatili hutolewa na$3x^3+14x^2−23x+6$. Upana wa mstatili hutolewa na$x+6$. Pata maelezo kwa urefu wa mstatili.

Suluhisho

$3x^2−4x+1$

Mlinganyo muhimu

Idara Algorithm$f(x)=d(x)q(x)+r(x)$ ambapo$q(x){\neq}0$

Dhana muhimu

• Mgawanyiko wa muda mrefu wa polynomial unaweza kutumika kugawanya polynomial na polynomial yoyote yenye shahada sawa au ya chini.
• Idara ya Algorithm inatuambia kwamba mgao wa polynomial unaweza kuandikwa kama bidhaa ya mgawanyiko na quotient aliongeza kwa salio.
• Mgawanyiko wa usanifu ni njia ya mkato ambayo inaweza kutumika kugawanya polynomial na binomial katika fomu$x−k.$
• Mgawanyiko wa Polynomial unaweza kutumika kutatua matatizo ya maombi, ikiwa ni pamoja na eneo na kiasi.

maelezo ya chini

$^1$National Park Service. “Lincoln Memorial Vifaa Takwimu.” www.nps.gov/linc/historycultu... statistics.htm. Ilipatikana 4/3/2014

faharasa

Idara ya Algorit

kupewa mgao polynomial$f(x)$ na yasiyo ya sifuri polynomial mgawanyiko$d(x)$ ambapo shahada ya$d(x)$ ni chini ya au sawa na shahada ya$f(x)$, kuna polynomials kipekee$q(x)$ na$r(x)$ kama kwamba$f(x)=d(x)q(x)+r(x)$ ambapo$q(x)$ ni quotient na$r(x)$ ni iliyobaki. Salio ni ama sawa na sifuri au ina shahada madhubuti chini ya$d(x)$.

mgawanyiko wa usanifu

njia ya mkato ambayo inaweza kutumika kugawanya polynomial na binomial ya fomu$x−k$