3.4: Grafu ya Kazi za Polynomial

Last updated
Save as PDF

Page ID: 181206

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Tambua sifa za grafu za kazi za polynomial.
Tumia factoring kupata zero za kazi za polynomial.
Tambua zero na wingi wao.
Kuamua tabia ya mwisho.
Kuelewa uhusiano kati ya shahada na pointi za kugeuka.
Grafu polynomial kazi.
Tumia Theorem ya Thamani ya Kati.

Mapato katika mamilioni ya dola kwa kampuni ya cable ya tamthiliya kutoka 2006 hadi 2013 inavyoonekana katika Jedwali$\PageIndex{1}$.

Jedwali$\PageIndex{1}$
Mwaka	2006	2007	2008	2009	2010	2011	2012	2013
Mapato	52.4	52.8	51.2	49.5	48.6	48.6	48.7	47.1

Mapato yanaweza kutajwa na kazi ya polynomial

\[R(t)=−0.037t^4+1.414t^3−19.777t^2+118.696t−205.332\]

ambapo$R$ inawakilisha mapato katika mamilioni ya dola na$t$ inawakilisha mwaka, na$t=6$ sambamba na 2006. Zaidi ya vipindi gani mapato ya kampuni yanaongezeka? Zaidi ya vipindi gani mapato ya kampuni hupungua? Maswali haya, pamoja na wengine wengi, yanaweza kujibiwa kwa kuchunguza grafu ya kazi ya polynomial. Tayari tumechunguza tabia ya ndani ya quadratics, kesi maalum ya polynomials. Katika sehemu hii sisi kuchunguza tabia ya ndani ya polynomials kwa ujumla.

Kutambua Tabia za Grafu za Kazi za Polynomial

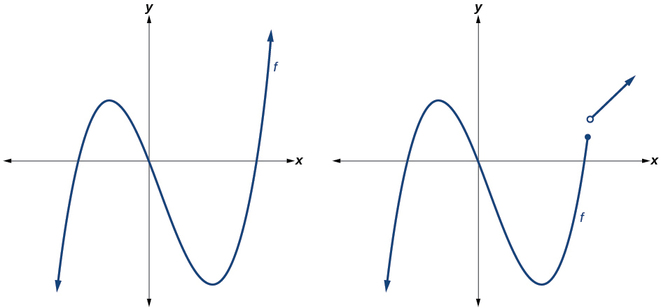
Kazi nyingi za shahada ya 2 au zaidi zina grafu ambazo hazina pembe kali; kumbuka kwamba aina hizi za grafu huitwa curves laini. Kazi za polynomial pia zinaonyesha grafu ambazo hazina mapumziko. Curves na mapumziko hakuna huitwa kuendelea. Kielelezo$\PageIndex{1}$ kinaonyesha grafu inayowakilisha kazi ya polynomial na grafu ambayo inawakilisha kazi ambayo si polynomial.

Grafu ya f (x) =x ^ 3-0.01x — Kielelezo$\PageIndex{1}$: Grafu ya$f(x)=x^3-0.01x$.

Mfano$\PageIndex{1}$: Recognizing Polynomial Functions

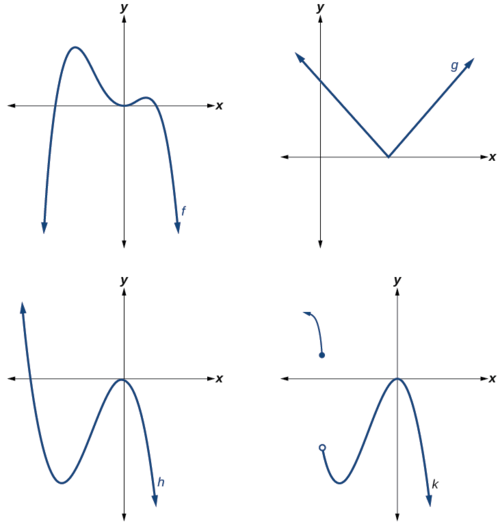
Ni ipi kati ya grafu katika Kielelezo$\PageIndex{2}$ inawakilisha kazi ya polynomial?

$Grafu mbili ambazo moja ina kazi ya polynomial na nyingine ina kazi kwa karibu inayofanana na polynomial lakini si. Grafu mbili ambazo moja ina kazi ya polynomial na nyingine ina kazi kwa karibu inayofanana na polynomial lakini si.$
Kielelezo$\PageIndex{2}$

Suluhisho

Grafu ya$f$ na$h$ ni grafu ya kazi za polynomial. Wao ni laini na inayoendelea.
Grafu ya$g$ na$k$ ni grafu ya kazi ambazo si polynomials. Grafu ya kazi$g$ ina kona kali. Grafu ya kazi$k$ haiendelei.

Q & A

Je! Kazi zote za polynomial zina kama uwanja wao wote namba halisi?

Ndiyo. Nambari yoyote halisi ni pembejeo halali kwa kazi ya polynomial.

Kutumia factoring Kupata Zeros ya Kazi Polynomial

Kumbuka kwamba ikiwa$f$ ni kazi ya polynomial, maadili ambayo$f(x)=0$ huitwa zero za$f$.$x$ Ikiwa equation ya kazi ya polynomial inaweza kuhesabiwa, tunaweza kuweka kila sababu sawa na sifuri na kutatua kwa zero.

Tunaweza kutumia njia hii ya kupata x-intercepts kwa sababu katika x-intercepts tunapata maadili pembejeo wakati thamani pato ni sifuri. Kwa polynomials ujumla, hii inaweza kuwa matarajio changamoto. Wakati quadratics inaweza kutatuliwa kwa kutumia formula rahisi quadratic, formula sambamba kwa polynomials za ujazo na ya nne ya shahada si rahisi kukumbuka, na formula hazipo kwa polynomials jumla ya shahada ya juu. Kwa hiyo, tutajiweka kwenye kesi tatu katika sehemu hii:

Polynomial inaweza kuzingatiwa kwa kutumia mbinu zinazojulikana: sababu kubwa ya kawaida na factoring trinomial.
Polynomial hutolewa kwa fomu iliyosababishwa.
Teknolojia hutumiwa kuamua intercepts.

HowTo: Kutokana na kazi ya polynomial$f$, find the x-intercepts by factoring

Weka$f(x)=0$.
Ikiwa kazi ya polynomial haipatikani kwa fomu iliyosababishwa:
1. Fanya nje mambo yoyote ya kawaida ya monomial.
2. Sababu yoyote binomials factorable au trinomials.
Weka kila sababu sawa na sifuri na kutatua kupata x-intercepts.

Mfano$\PageIndex{2}$: Finding the x-Intercepts of a Polynomial Function by Factoring

Kupata x-intercepts ya$f(x)=x^6−3x^4+2x^2$.

Suluhisho

Tunaweza kujaribu sababu polynomial hii ili kupata ufumbuzi kwa$f(x)=0$.

\[\begin{align*} x^6−3x^4+2x^2&=0 & &\text{Factor out the greatest common factor.} \\ x^2(x^4−3x^2+2)&=0 & &\text{Factor the trinomial.} \\ x^2(x^2−1)(x^2−2)&=0 & &\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x^2&=0 & & & (x^2−1)&=0 & & & (x^2−2)&=0 \\ x^2&=0 & &\text{ or } & x^2&=1 & &\text{ or } & x^2&=2 \\ x&=0 &&& x&={\pm}1 &&& x&={\pm}\sqrt{2} \end{align*}\].

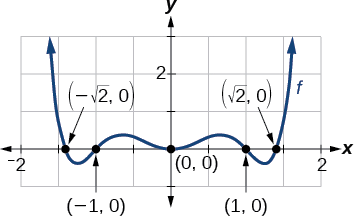
Hii inatupa tano x-intercepts:$(0,0)$,$(1,0)$,$(−1,0)$,$(\sqrt{2},0)$, na$(−\sqrt{2},0)$ (Kielelezo$\PageIndex{3}$). Tunaweza kuona kwamba hii ni hata kazi.

Mfano$\PageIndex{3}$: Finding the x-Intercepts of a Polynomial Function by Factoring

Kupata x-intercepts ya$f(x)=x^3−5x^2−x+5$.

Suluhisho

Kupata ufumbuzi$f(x)=0$ kwa factoring.

\[\begin{align*} x^3−5x^2−x+5&=0 &\text{Factor by grouping.} \\ x^2(x−5)−(x−5)&=0 &\text{Factor out the common factor.} \\ (x^2−1)(x−5)&=0 &\text{Factor the difference of squares.} \\ (x+1)(x−1)(x−5)&=0 &\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x+1&=0 & &\text{or} & x−1&=0 & &\text{or} & x−5&=0 \\ x&=−1 &&& x&=1 &&& x&=5\end{align*}\]

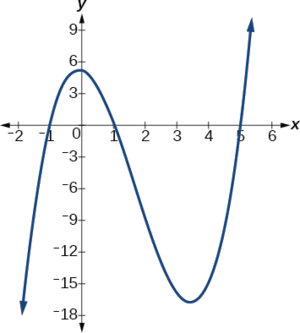
Kuna tatu x-intercepts:$(−1,0)$,$(1,0)$, na$(5,0)$ (Kielelezo$\PageIndex{4}$).

Grafu ya f (x) =x ^ 3-5x ^ 2-x+5 na mikataba yake mitatu (-1, 0), (1, 0), na (5, 0). — Kielelezo$\PageIndex{4}$: Grafu ya$f(x)$.

Mfano$\PageIndex{4}$: Finding the y- and x-Intercepts of a Polynomial in Factored Form

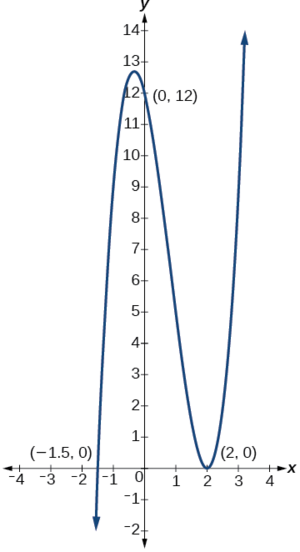
Kupata y- na x-intercepts ya$g(x)=(x−2)^2(2x+3)$.

Suluhisho

Y-intercept inaweza kupatikana kwa kutathmini$g(0)$.

\[\begin{align*} g(0)&=(0−2)^2(2(0)+3) \\ &=12 \end{align*}\]

Hivyo y-intercept ni$(0,12)$.

Ya x-intercepts inaweza kupatikana kwa kutatua$g(x)=0$.

\[(x−2)^2(2x+3)=0\]

\[\begin{align*} (x−2)^2&=0 & & & (2x+3)&=0 \\ x−2&=0 & &\text{or} & x&=−\dfrac{3}{2} \\ x&=2 \end{align*}\]

Hivyo x-intercepts ni$(2,0)$ na$\left(−\dfrac{3}{2},0\right)$.

Uchambuzi

Tunaweza daima kuangalia kwamba majibu yetu ni busara kwa kutumia calculator graph kwa grafu polynomial kama inavyoonekana katika Kielelezo$\PageIndex{5}$.

Grafu ya g (x) = (x-2) ^2 (2x+3) na x-intercepts zake mbili (2, 0) na (-3/2, 0) na y-intercept yake (0, 12). — Kielelezo$\PageIndex{5}$: Grafu ya$g(x)$.

Mfano$\PageIndex{5}$: Finding the x-Intercepts of a Polynomial Function Using a Graph

Kupata x-intercepts ya$h(x)=x^3+4x^2+x−6$.

Suluhisho

Polynomial hii si katika fomu factored, haina mambo ya kawaida, na haionekani kuwa factorable kutumia mbinu awali kujadiliwa. Kwa bahati nzuri, tunaweza kutumia teknolojia ili kupata intercepts. Kumbuka kwamba baadhi ya maadili hufanya graphing vigumu kwa mkono. Katika kesi hizi, tunaweza kuchukua faida ya huduma za kuchora.

Kuangalia grafu ya kazi hii, kama inavyoonekana kwenye Kielelezo$\PageIndex{6}$, inaonekana kwamba kuna x-intercepts saa$x=−3,−2, \text{ and }1$.

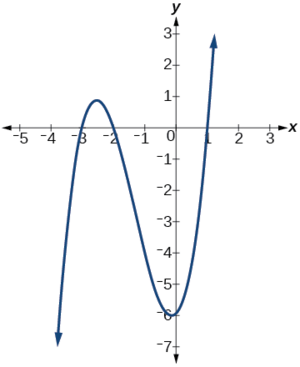
Grafu ya h (x) =x ^ 3+4x^2+x-6. — Kielelezo$\PageIndex{6}$: Grafu ya$h(x)$.

Tunaweza kuangalia kama haya ni sahihi kwa kubadili maadili haya$x$ na kuthibitisha hilo
\[h(−3)=h(−2)=h(1)=0. \nonumber\]

Tangu$h(x)=x^3+4x^2+x−6$, tuna:

\[ \begin{align*} h(−3)&=(−3)^3+4(−3)^2+(−3)−6=−27+36−3−6=0 \\[4pt] h(−2) &=(−2)^3+4(−2)^2+(−2)−6 =−8+16−2−6=0 \\[4pt] h(1)&=(1)^3+4(1)^2+(1)−6=1+4+1−6=0 \end{align*}\]

Kila x-intercept inalingana na sifuri ya kazi polynomial na kila sifuri hutoa sababu, hivyo sasa tunaweza kuandika polynomial katika fomu factored.

\[\begin{align*} h(x)&=x^3+4x^2+x−6 \\ &=(x+3)(x+2)(x−1) \end{align*}\]

Zoezi$\PageIndex{1}$

Pata y-na x-intercepts ya kazi$f(x)=x^4−19x^2+30x$.

Jibu

y-kukatiza$(0,0)$;
x-intercepts$(0,0)$$(–5,0)$,$(2,0)$,, na$(3,0)$

Kutambua Zero na Wengi wao

Grafu hufanya tofauti katika x-intercepts mbalimbali. Wakati mwingine, grafu itavuka juu ya mhimili usio na usawa wakati wa kupinga. Wakati mwingine, grafu itagusa mhimili usio na usawa na kuacha. Tuseme, kwa mfano, sisi grafu kazi

\[f(x)=(x+3)(x−2)^2(x+1)^3.\]

Angalia katika Kielelezo$\PageIndex{7}$ kwamba tabia ya kazi katika kila moja ya x-intercepts ni tofauti.

X-intercept -3 ni suluhisho la equation$(x+3)=0$. Grafu hupita moja kwa moja kwa njia ya-intercept saa$x=−3$. Sababu ni linear (ina shahada ya 1), hivyo tabia karibu na intercept ni kama ile ya mstari-inapita moja kwa moja kupitia intercept. Tunaita hii sifuri moja kwa sababu sifuri sambamba na sababu moja ya kazi.

X-intercept 2 ni suluhisho la mara kwa mara la equation$(x−2)^2=0$. Grafu inagusa mhimili wakati wa kupinga na kubadilisha mwelekeo. Sababu ni quadratic (shahada 2), hivyo tabia karibu intercept ni kama ile ya quadratic - ni bounces mbali ya mhimili usawa katika intercept.

\[(x−2)^2=(x−2)(x−2)\]

Sababu ni mara kwa mara, yaani, sababu$(x−2)$ inaonekana mara mbili. Idadi ya nyakati sababu iliyotolewa inaonekana katika fomu iliyosababishwa ya equation ya polynomial inaitwa wingi. Zero zinazohusiana na jambo hili$x=2$,, ina wingi 2 kwa sababu sababu$(x−2)$ hutokea mara mbili.

X-intercept -1 ni suluhisho la mara kwa mara la$(x+1)^3=0$ sababu.Grafu hupita kupitia mhimili kwenye kizuizi, lakini hupiga kidogo kwanza. Sababu hii ni ujazo (shahada 3), hivyo tabia karibu intercept ni kama ile ya mchemraba-na huo S-sura karibu intercept kama kazi toolkit$f(x)=x^3$. Tunaita hii sifuri tatu, au sifuri na wingi 3.

Kwa zero na hata kuzidisha, grafu hugusa au ni tangent kwa x-axis. Kwa zero na kuzidisha isiyo ya kawaida, grafu huvuka au kuingiliana na x-axis. Angalia Kielelezo$\PageIndex{8}$ kwa mifano ya grafu ya kazi za polynomial na wingi 1, 2, na 3.

Kielelezo$\PageIndex{8}$: Grafu tatu zinaonyesha kazi tatu tofauti za polynomial na wingi 1, 2, na 3.

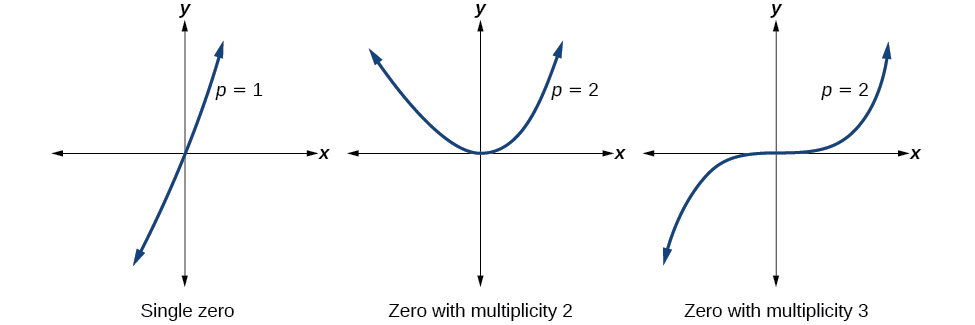
Kwa nguvu za juu hata, kama vile 4, 6, na 8, grafu bado itagusa na kuondokana na mhimili usio na usawa lakini, kwa kila kuongezeka hata nguvu, grafu itaonekana kuwa ya kupendeza kama inakaribia na kuacha x-axis.

Kwa nguvu za juu isiyo ya kawaida, kama vile 5, 7, na 9, grafu bado itavuka kupitia mhimili usio na usawa, lakini kwa kila nguvu isiyo ya kawaida ya kuongezeka, grafu itaonekana kama inakaribia na kuacha mhimili wa x.

Tabia ya picha ya Polynomials katika X-intercepts

Ikiwa polynomial ina sababu ya fomu$(x−h)^p$, tabia karibu na x-intercepth imedhamiriwa na nguvu$p$. Tunasema kwamba$x=h$ ni sifuri ya wingi$p$.

Grafu ya kazi ya polynomial itagusa x-axis kwenye zero na hata kuzidisha. Grafu itavuka x-axis kwenye zero na kuzidisha isiyo ya kawaida.

Jumla ya kuzidisha ni kiwango cha kazi ya polynomial.

HOWTO: Kutokana na grafu ya kazi ya polynomial ya shahada$n$, identify the zeros and their multiplicities

Ikiwa grafu inavuka x-axis na inaonekana karibu linear katika intercept, ni sifuri moja.
Ikiwa grafu inagusa mhimili wa x-x na huondoka kwenye mhimili, ni sifuri na hata wingi.
Ikiwa grafu inavuka mhimili wa x kwenye sifuri, ni sifuri na wingi usio wa kawaida.
Jumla ya wingi ni$n$.

Mfano$\PageIndex{6}$: Identifying Zeros and Their Multiplicities

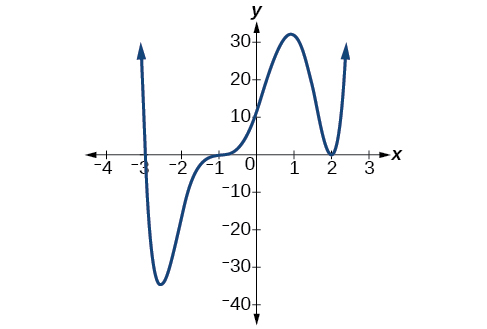
Tumia grafu ya kazi ya shahada ya 6 katika Kielelezo$\PageIndex{9}$ ili kutambua zero za kazi na kuzidisha kwao iwezekanavyo.

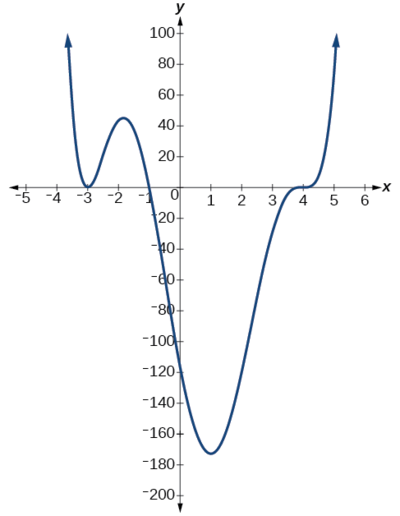
Grafu ya polynomial hata shahada na shahada 6. — Kielelezo$\PageIndex{9}$: Grafu ya kazi ya polynomial na shahada ya 5.

Suluhisho

Kazi ya polynomial ni ya shahada$n$. Jumla ya wingi lazima iwe$n$.

Kuanzia upande wa kushoto, sifuri ya kwanza hutokea$x=−3$. Grafu inagusa x-axis, hivyo wingi wa sifuri lazima iwe hata. Sifuri ya 1-3 ina msururu 2.

Zero ijayo hutokea$x=−1$. Grafu inaonekana karibu linear katika hatua hii. Hii ni sifuri moja ya wingi 1.

Zero ya mwisho hutokea$x=4$ katika.Grafu huvuka mstari wa x-axis, hivyo upeo wa sifuri lazima uwe usio wa kawaida. Tunajua kwamba msururu ni uwezekano 3 na kwamba jumla ya wingi ni uwezekano 6.

Zoezi$\PageIndex{2}$

Tumia grafu ya kazi ya shahada ya 5 katika Kielelezo$\PageIndex{10}$ ili kutambua zero za kazi na wingi wao.

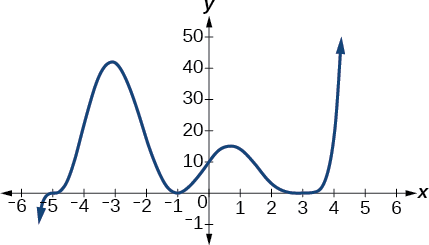
$Grafu ya kazi ya polynomial na shahada ya 5.$

Kielelezo$\PageIndex{10}$: Grafu ya kazi ya polynomial na shahada ya 5.

Jibu: Grafu ina sifuri ya —5 yenye msururu 1, sifuri ya -1 yenye wingi 2, na sifuri ya 3 na hata msururu.

Kuamua Mwisho Tabia

Kama tulivyojifunza, tabia ya grafu ya kazi ya polynomial ya fomu

\[f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0\]

ama hatimaye kupanda au kuanguka kama$x$ ongezeko bila amefungwa na ama kupanda au kuanguka kama$x$ itapungua bila amefungwa. Hii ni kwa sababu kwa pembejeo kubwa sana, sema 100 au 1,000, neno linaloongoza linatawala ukubwa wa pato. Vile vile ni kweli kwa pembejeo ndogo sana, sema -100 au —1,000.

Kumbuka kwamba tunaita tabia hii tabia ya mwisho ya kazi. Kama tulivyosema wakati wa kujadili equations quadratic, wakati mrefu inayoongoza ya kazi ya polynomial$a_nx^n$, ni hata kazi ya nguvu, kama$x$ ongezeko au hupungua bila kufungwa,$f(x)$ huongezeka bila kufungwa. Wakati mrefu kuongoza ni isiyo ya kawaida nguvu kazi, kama$x$ itapungua bila kufungwa,$f(x)$ pia itapungua bila amefungwa; kama$x$ ongezeko bila amefungwa,$f(x)$ pia kuongezeka bila amefungwa. Ikiwa neno linaloongoza ni hasi, litabadilisha mwelekeo wa tabia ya mwisho. $\PageIndex{11}$Kielelezo kinafupisha kesi zote nne.

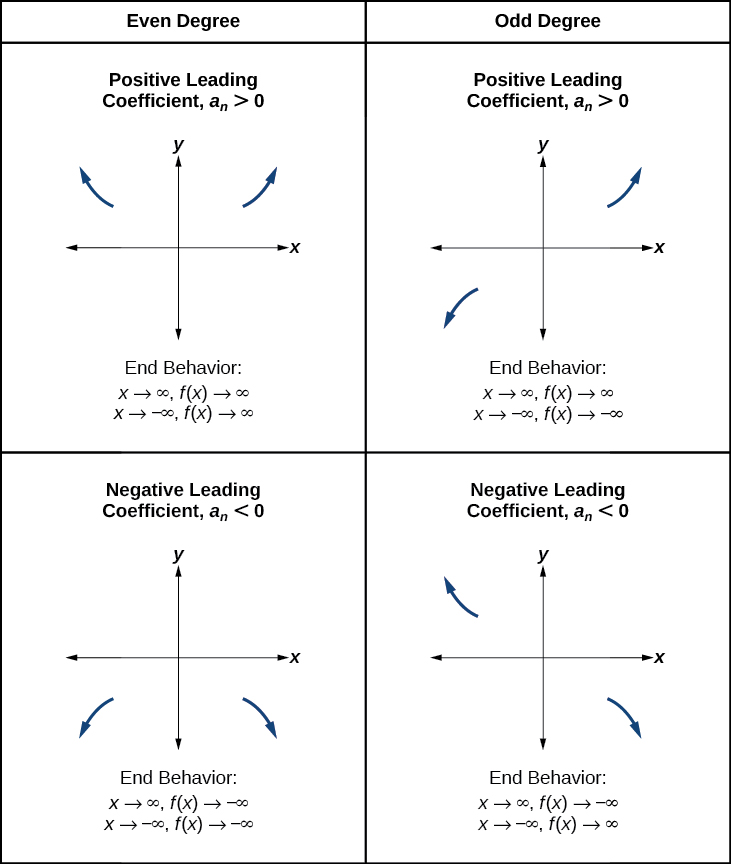
Jedwali kuonyesha tabia ya mwisho ya isiyo ya kawaida na hata polynomials na coefficients chanya na hasi — Kielelezo$\PageIndex{11}$.

Kuelewa Uhusiano kati ya Shahada na Pointi za Kugeuka

Mbali na tabia ya mwisho, kukumbuka kwamba tunaweza kuchambua tabia polynomial kazi ya ndani. Inaweza kuwa na hatua ya kugeuka ambapo grafu inabadilika kuongezeka hadi kupungua (kupanda hadi kuanguka) au kupungua kwa kuongezeka (kuanguka kwa kupanda). Angalia grafu ya kazi ya polynomial$f(x)=x^4−x^3−4x^2+4x$ katika Kielelezo$\PageIndex{12}$. Grafu ina pointi tatu za kugeuka.

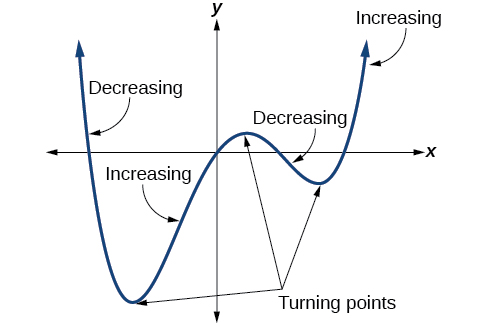
Grafu ya f (x) =x ^ 4-x ^ 3-4x^2+4x ambayo inaashiria ambapo kazi huongezeka na kupungua na pointi zake za kugeuka. — Kielelezo$\PageIndex{12}$: Grafu ya$f(x)=x^4-x^3-4x^2+4x$

Kazi hii$f$ ni kazi ya shahada ya 4 ya polynomial na ina pointi 3 za kugeuka. Idadi ya juu ya pointi za kugeuka za kazi ya polynomial daima ni moja chini ya kiwango cha kazi.

Ufafanuzi: Kutafsiri Pointi za Ku

Hatua ya kugeuka ni hatua ya grafu ambapo grafu inabadilika kutoka kuongezeka hadi kupungua (kupanda hadi kuanguka) au kupungua kwa kuongezeka (kuanguka kwa kupanda). Polynomial ya shahada$n$ itakuwa na pointi nyingi za$n−1$ kugeuka.

Mfano$\PageIndex{7}$: Finding the Maximum Number of Turning Points Using the Degree of a Polynomial Function

Pata idadi kubwa ya pointi za kugeuka za kila kazi ya polynomial.

$f(x)=−x^3+4x^5−3x^2+1$
$f(x)=−(x−1)^2(1+2x^2)$

Suluhisho

a.$f(x)=−x^3+4x^5−3x^2+1$

Kwanza, fungua upya kazi ya polynomial katika utaratibu wa kushuka:$f(x)=4x^5−x^3−3x^2+1$

Tambua kiwango cha kazi ya polynomial. Kazi hii ya polynomial ni ya shahada ya 5.

Idadi ya juu ya pointi za kugeuka ni$5−1=4$.

b.$f(x)=−(x−1)^2(1+2x^2)$

Kwanza, tambua muda wa kuongoza wa kazi ya polynomial ikiwa kazi ilipanuliwa.

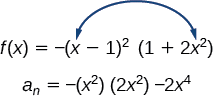
$imageedit_33_3540887475.png$

Kisha, tambua kiwango cha kazi ya polynomial. Kazi hii ya polynomial ni ya shahada ya 4.

Idadi ya juu ya pointi za kugeuka ni$4−1=3$.

Graphing Kazi Polynomial

Tunaweza kutumia kile tulichojifunza kuhusu kuzidisha, tabia ya mwisho, na pointi za kugeuka kwenye michoro za mchoro wa kazi nyingi. Hebu tuweke haya yote pamoja na tuangalie hatua zinazohitajika kwa graph kazi za polynomial.

Jinsi ya: Kutokana na kazi ya polynomial, mchoro grafu

Kupata intercepts.
Angalia ulinganifu. Ikiwa kazi ni kazi hata, grafu yake ni ya kawaida kuhusu mhimili wa y, yaani,$f(−x)=f(x)$. Ikiwa kazi ni kazi isiyo ya kawaida, grafu yake ni ya kawaida kuhusu asili, yaani,$f(−x)=−f(x)$.
Tumia wingi wa zero ili kuamua tabia ya polynomial kwenye x-intercepts.
Kuamua tabia ya mwisho kwa kuchunguza muda wa kuongoza.
Tumia tabia ya mwisho na tabia katika intercepts kwa mchoro grafu.
Hakikisha kwamba idadi ya pointi za kugeuka hazizidi moja chini ya kiwango cha polynomial.
Kwa hiari, tumia teknolojia ili uangalie grafu.

Mfano$\PageIndex{8}$: Sketching the Graph of a Polynomial Function

Mchoro grafu ya$f(x)=−2(x+3)^2(x−5)$.

Suluhisho

Grafu hii ina x-intercepts mbili. Kwa$x=−3$, sababu hiyo ni mraba, inayoonyesha wingi wa 2. Grafu itapungua kwenye x-intercept hii. Kwa$x=5$, kazi ina wingi wa moja, kuonyesha grafu itavuka kupitia mhimili kwenye kizuizi hiki.

Y-intercept hupatikana kwa kutathmini$f(0)$.

\[\begin{align*} f(0)&=−2(0+3)^2(0−5) \\ &=−2⋅9⋅(−5) \\ &=90 \end{align*}\]

Y-intercept ni$(0,90)$.

Zaidi ya hayo, tunaweza kuona mrefu kuongoza, kama polynomial hii walikuwa tele nje, itakuwa$−2x3$, hivyo tabia ya mwisho ni ile ya ujazo wima yalijitokeza, na matokeo kupungua kama pembejeo mbinu infinity, na matokeo kuongezeka kama mbinu pembejeo infinity hasi. Angalia Kielelezo$\PageIndex{13}$.

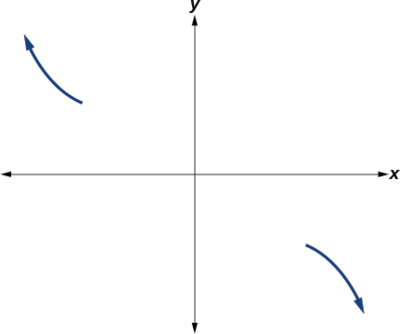
Kielelezo$\PageIndex{13}$: Kuonyesha usambazaji kwa muda wa kuongoza.

Ili mchoro huu, tunaona kwamba:

Kama$x{\rightarrow}−{\infty}$ kazi$f(x){\rightarrow}{\infty}$, hivyo tunajua graph kuanza katika roboduara ya pili na ni kupungua kuelekea x-axis.
Kwa kuwa$f(−x)=−2(−x+3)^2(−x–5)$ si sawa na$f(x)$, grafu haina kuonyesha ulinganifu.
Kwa$(−3,0)$, grafu inaondoka kwenye mhimili wa x, hivyo kazi lazima ianze kuongezeka.
Katika$(0,90)$, grafu huvuka mhimili wa y kwenye y-intercept. Angalia Kielelezo$\PageIndex{14}$.

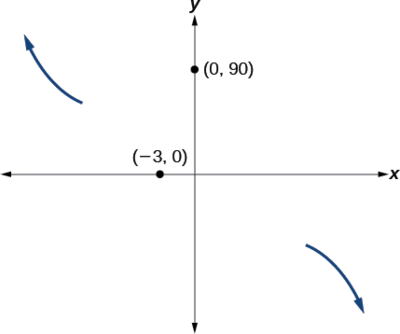
Grafu ya tabia ya mwisho na inakataza, (-3, 0) na (0, 90), kwa kazi f (x) =-2 (x+3) ^2 (x-5). — Kielelezo$\PageIndex{14}$: Grafu ya tabia ya mwisho na inakataza$(0, 90)$,$(-3, 0)$ na, kwa kazi$f(x)=-2(x+3)^2(x-5)$.

Mahali fulani baada ya hatua hii, grafu inapaswa kurejea chini au kuanza kupungua kuelekea mhimili usio na usawa kwa sababu grafu inapita kupitia intercept ijayo$(5,0)$. Angalia Kielelezo$\PageIndex{15}$.

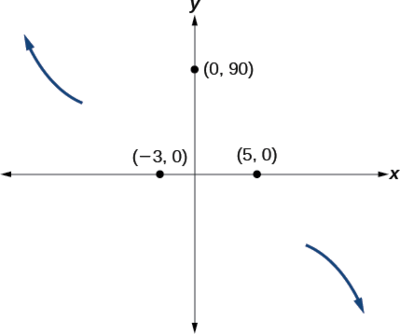
Grafu ya tabia ya mwisho na inakataza, (-3, 0), (0, 90) na (5, 0), kwa kazi f (x) =-2 (x+3) ^2 (x-5). — Kielelezo$\PageIndex{15}$: Grafu ya tabia ya mwisho na inakataza$(-3, 0)$,$(5, 0)$,$(0, 90)$ na, kwa kazi$f(x)=-2(x+3)^2(x-5)$.

Kama$x{\rightarrow}{\infty}$ kazi$f(x){\rightarrow}−{\infty}$,

hivyo tunajua grafu inaendelea kupungua, na tunaweza kuacha kuchora grafu katika roboduara ya nne.

Kutumia teknolojia, tunaweza kuunda grafu kwa kazi ya polynomial, iliyoonyeshwa kwenye Kielelezo$\PageIndex{16}$, na uhakikishe kuwa grafu inayoonekana inaonekana kama mchoro wetu kwenye Kielelezo$\PageIndex{15}$.

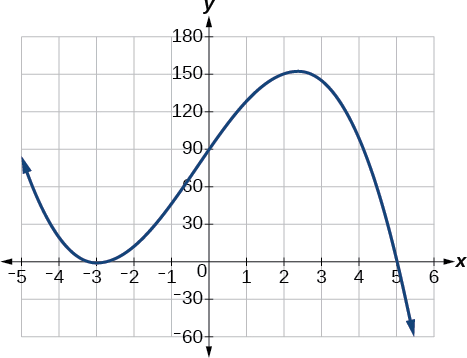
$Grafu kamili ya kazi ya polynomial f (x) =-1 (x+3) ^2 (x-5)$
Kielelezo$\PageIndex{16}$: Grafu kamili ya kazi ya polynomial$f(x)=−2(x+3)^2(x−5)$.

Zoezi$\PageIndex{8}$

Mchoro grafu ya$f(x)=\dfrac{1}{4}x(x−1)^4(x+3)^3$.

Jibu: $alt$
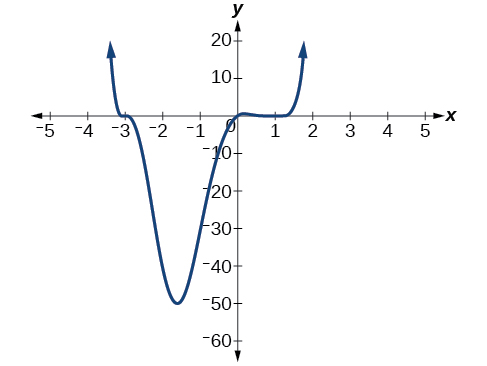
Kielelezo$\PageIndex{17}$: Grafu ya$f(x)=\frac{1}{4}x(x−1)^4(x+3)^3$

Kutumia Theorem ya Thamani ya Kati

Katika hali fulani, tunaweza kujua pointi mbili kwenye grafu lakini sio zero. Ikiwa pointi hizo mbili ziko kwenye pande tofauti za x-axis, tunaweza kuthibitisha kuwa kuna sifuri kati yao. Fikiria kazi ya polynomial$f$ ambayo grafu ni laini na inayoendelea. Theorem Theorem ya Thamani ya Kati inasema kwamba kwa namba mbili$a$$a<b$ na$b$ katika uwanja wa$f$$f(a){\neq}f(b)$, ikiwa na, basi kazi$f$ inachukua kila thamani kati$f(a)$ na$f(b)$. Tunaweza kutumia theorem hii kwa kesi maalum ambayo ni muhimu katika kuchora kazi za polynomial. Ikiwa hatua kwenye grafu ya kazi$f$ inayoendelea$x=a$ iko juu ya mhimili wa x na hatua nyingine$x=b$ iko chini yax-axis, kuna lazima kuwepo hatua ya tatu kati$x=a$ na$x=b$ ambapo grafu huvuka x-axis. Piga hatua$(c,f(c))$ hii.Hii ina maana kwamba tuna uhakika kuna suluhisho$c$ ambapo$f(c)=0$.

Kwa maneno mengine, Theorem ya Theorem ya Thamani ya Kati inatuambia kwamba wakati kazi ya polynomial inabadilika kutoka thamani hasi kwa thamani nzuri, kazi inapaswa kuvuka x-axis. Kielelezo$\PageIndex{18}$ kinaonyesha kwamba kuna sifuri kati$a$ na$b$.

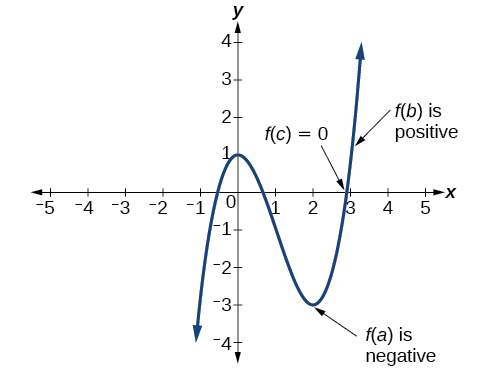
Grafu ya kazi isiyo ya kawaida ya shahada ya polynomial inayoonyesha hatua f (a) hiyo ni hasi, f (b) hiyo ni chanya, na f (c) hiyo ni 0. — Kielelezo$\PageIndex{18}$: Kutumia Theorem ya Thamani ya Kati ili kuonyesha kuna sifuri.

Ufafanuzi: Theorem ya Thamani ya Kati

Hebu$f$ iwe kazi ya polynomial. Theorem ya Theorem ya Thamani ya Kati inasema kwamba ikiwa$f(a)$ na$f(b)$ kuwa na ishara tofauti, basi kuna angalau thamani moja$c$ kati$a$ na$b$ ambayo$f(c)=0$.

Mfano$\PageIndex{9}$: Using the Intermediate Value Theorem

Onyesha kuwa kazi$f(x)=x^3−5x^2+3x+6$ ina angalau zeros mbili halisi kati$x=1$ na$x=4$.

Suluhisho

Kama mwanzo, tathmini$f(x)$ kwa maadili ya integer$x=1,\;2,\;3,\; \text{and }4$ (Jedwali$\PageIndex{2}$).

Jedwali$\PageIndex{2}$
$x$	1	2	3	4
$f(x)$	5	0	-3	2

Tunaona kwamba sifuri moja hutokea$x=2$. Pia,$f(3)$ kwa kuwa ni hasi na$f(4)$ ni chanya, na Theorem ya Theorem ya Thamani ya Kati, lazima iwe na angalau moja ya sifuri halisi kati ya 3 na 4.

Tumeonyesha kuwa kuna angalau zeros mbili halisi kati$x=1$ na$x=4$.

Uchambuzi

Pia tunaweza kuona kwenye graph ya kazi katika Kielelezo$\PageIndex{19}$ kwamba kuna mbili zeros halisi kati$x=1$ na$x=4$.

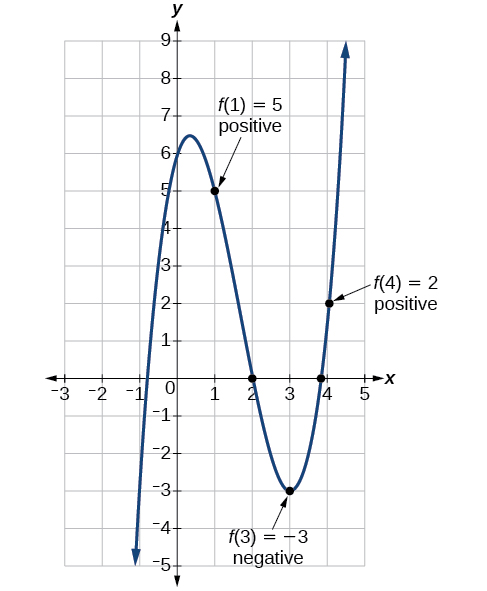
Grafu ya f (x) =x ^ 3-5x ^ 2+3x+6 na inaonyesha, na Theorem ya Thamani ya Kati, kwamba kuna zero mbili tangu f (1) =5 na f (4) =2 ni chanya na f (3) = -3 ni hasi. — Kielelezo$\PageIndex{19}$.

Zoezi$\PageIndex{4}$

Onyesha kwamba kazi$f(x)=7x^5−9x^4−x^2$ ina angalau moja sifuri halisi kati$x=1$ na$x=2$.

Jibu: Kwa sababu$f$ ni kazi polynomial na tangu$f(1)$ ni hasi na$f(2)$ ni chanya, kuna angalau moja sifuri halisi kati$x=1$ na$x=2$.

Kuandika Formula kwa Kazi za Polynomial

Sasa kwa kuwa tunajua jinsi ya kupata zero za kazi nyingi, tunaweza kuzitumia kuandika formula kulingana na grafu. Kwa sababu kazi polynomial iliyoandikwa katika fomu factored itakuwa na x-intercept ambapo kila sababu ni sawa na sifuri, tunaweza kuunda kazi ambayo itapita kupitia seti ya x-intercepts kwa kuanzisha seti sambamba ya mambo.

Kumbuka: Factored Fomu ya Polynomials

Ikiwa polynomial ya shahada ya chini$p$ ina intercepts usawa katika$x=x_1,x_2,…,x_n$, basi polynomial inaweza kuandikwa katika fomu factored:$f(x)=a(x−x_1)^{p_1}(x−x_2)^{p_2}⋯(x−x_n)^{p_n}$ ambapo nguvu$p_i$ juu ya kila sababu inaweza kuamua na tabia ya grafu katika intercept sambamba, na sababu ya kunyoosha$a$ inaweza kuamua kupewa thamani ya kazi zaidi ya x-intercept.

$alt$ Kutokana na grafu ya kazi ya polynomial, weka fomu ya kazi.

Tambua x-intercepts ya grafu ili kupata sababu za polynomial.
Kuchunguza tabia ya grafu katika x-intercepts kuamua wingi wa kila sababu.
Pata polynomial ya shahada ndogo iliyo na mambo yote yaliyopatikana katika hatua ya awali.
Tumia hatua nyingine yoyote kwenye grafu (y-intercept inaweza kuwa rahisi) kuamua sababu ya kunyoosha.

Mfano$\PageIndex{10}$: Writing a Formula for a Polynomial Function from the Graph

Andika fomu ya kazi ya polynomial iliyoonyeshwa kwenye Kielelezo$\PageIndex{20}$.

Grafu ya polynomial chanya hata-shahada na zero katika x=-3, 2, 5 na y =-2. — Kielelezo$\PageIndex{20}$.

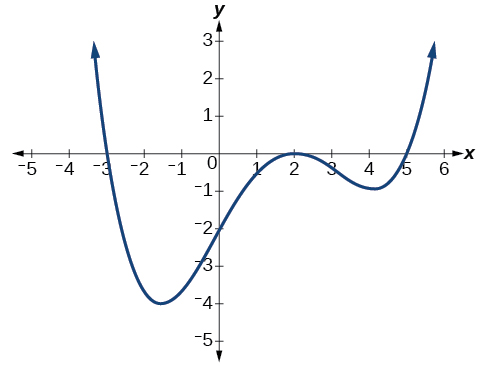
Suluhisho

Grafu hii ina tatu x-intercepts:$x=−3,\;2,\text{ and }5$. Y-intercept iko$(0,2)$ katika.Katika$x=−3$ na$ x=5$, grafu hupita kupitia mstari wa mhimili, na kupendekeza mambo yanayofanana ya polynomial yatakuwa ya mstari. Katika$x=2$, graph bounces katika intercept, na kupendekeza sababu sambamba ya polynomial itakuwa shahada ya pili (quadratic). Pamoja, hii inatupa

\[f(x)=a(x+3)(x−2)^2(x−5)\]

Kuamua sababu ya kunyoosha, tunatumia hatua nyingine kwenye grafu. Tutatumia y-intercept$(0,–2)$, kutatua kwa$a$.

\[\begin{align*} f(0)&=a(0+3)(0−2)^2(0−5) \\ −2&=a(0+3)(0−2)^2(0−5) \\ −2&=−60a \\ a&=\dfrac{1}{30} \end{align*}\]

Polynomial iliyochapishwa inaonekana kuwakilisha kazi$f(x)=\dfrac{1}{30}(x+3)(x−2)^2(x−5)$.

Zoezi$\PageIndex{5}$

Kutokana na grafu iliyoonyeshwa kwenye Kielelezo$\PageIndex{21}$, weka fomu ya kazi iliyoonyeshwa.

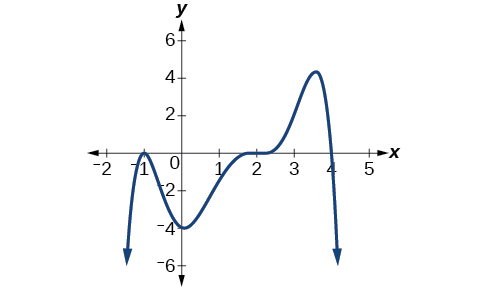
Grafu ya polynomial hasi hata-shahada na zero katika x=-1, 2, 4 na y = -4. — Kielelezo$\PageIndex{21}$.

Jibu: $f(x)=−\frac{1}{8}(x−2)^3(x+1)^2(x−4)$

Kutumia Extrema za Mitaa na Global

Kwa quadratics, tuliweza kupata thamani ya juu au ya chini ya kazi kwa kutafuta vertex. Kwa polynomials jumla, kutafuta pointi hizi kugeuka haiwezekani bila mbinu za juu zaidi kutoka calculus. Hata hivyo, kutafuta ambapo extrema kutokea bado inaweza algebraically changamoto. Kwa sasa, tutakadiria maeneo ya pointi za kugeuka kwa kutumia teknolojia ili kuzalisha grafu.

Kila hatua ya kugeuka inawakilisha kiwango cha chini au kiwango cha juu. Wakati mwingine, hatua ya kugeuka ni hatua ya juu au ya chini kabisa kwenye grafu nzima. Katika kesi hizi, tunasema kuwa hatua ya kugeuka ni kiwango cha juu cha kimataifa au kiwango cha chini cha kimataifa. Hizi pia hujulikana kama kiwango cha juu kabisa na maadili ya chini kabisa ya kazi.

Kumbuka: Extrema ya Mitaa na ya Kimataifa

Upeo wa ndani au kiwango cha chini cha ndani$x=a$ (wakati mwingine huitwa upeo wa jamaa au kiwango cha chini, kwa mtiririko huo) ni pato kwa kiwango cha juu au cha chini kabisa kwenye grafu katika kipindi cha wazi$x=a$ karibu.Ikiwa kazi ina kiwango cha juu cha ndani$a$, basi$f(a){\geq}f(x)$ kwa wote $x$katika kipindi cha wazi kote$x=a$. Ikiwa kazi ina kiwango cha chini cha ndani$a$, basi$f(a){\leq}f(x)$ kwa wote$x$ katika kipindi cha wazi kote$x=a$.

Upeo wa kimataifa au kiwango cha chini cha kimataifa ni pato kwenye hatua ya juu au ya chini ya kazi. Ikiwa kazi ina kiwango cha juu cha kimataifa$a$, basi$f(a){\geq}f(x)$ kwa wote$x$. Ikiwa kazi ina kiwango cha chini cha kimataifa$a$, basi$f(a){\leq}f(x)$ kwa wote$x$.

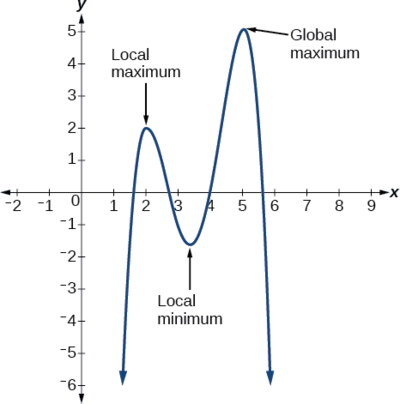
Tunaweza kuona tofauti kati ya extrema ndani na kimataifa katika Kielelezo$\PageIndex{22}$.

Kielelezo$\PageIndex{22}$: Grafu ya polynomial hata shahada ambayo inaashiria upeo wa ndani na kiwango cha chini na kiwango cha juu cha kimataifa.

$alt$ Je! Kazi zote za polynomial zina kiwango cha chini au kiwango cha juu cha kimataifa?

Hapana. Kazi za polynomial tu za shahada hata zina kiwango cha chini cha kimataifa au kiwango cha juu. Kwa mfano,$f(x)=x$ haina upeo wa kimataifa wala kiwango cha chini cha kimataifa.

Mfano$\PageIndex{11}$: Using Local Extrema to Solve Applications

Sanduku la wazi linapaswa kujengwa kwa kukata mraba kutoka kila kona ya cm 14 na karatasi 20 cm ya plastiki kisha kukunja pande. Pata ukubwa wa mraba ambao unapaswa kukatwa ili kuongeza kiasi kilichofungwa na sanduku.

Suluhisho

Tutaanza tatizo hili kwa kuchora picha kama hiyo katika Kielelezo$\PageIndex{23}$, kuipatia upana wa mraba uliokatwa na kutofautiana,$w$.

Kielelezo$\PageIndex{23}$: Mchoro wa mstatili na mraba nne kwenye pembe.

Kumbuka kwamba baada ya mraba kukatwa kutoka kila mwisho, inacha$a(14−2w)$ cm na$(20−2w)$ cm mstatili kwa msingi wa sanduku, na sanduku litakuwa$w$ urefu wa cm. Hii inatoa kiasi

\[\begin{align*} V(w)&=(20−2w)(14−2w)w \\ &=280w−68w^2+4w^3 \end{align*}\]

Angalia, kwa kuwa sababu ni$20–2w$$14–2w$, na$w$, zero tatu ni$10, \,7,$ na$0,) respectively. Because a height of \(0$ cm si busara, tunaona tu zero$10$ na$7.$ upande mfupi ni$14$ na sisi ni kukata mraba mbili, hivyo maadili$w$ inaweza kuchukua ni zaidi ya sifuri au chini ya$7.$ Hii ina maana sisi kuzuia uwanja wa kazi hii kwa$0<w<7$ .Kutumia teknolojia mchoro grafu ya$V(w)$ juu ya uwanja huu busara, sisi kupata grafu kama kwamba katika Kielelezo$\PageIndex{24}$. Tunaweza kutumia grafu hii kukadiria thamani ya kiwango cha juu kwa kiasi, vikwazo kwa maadili kwa$w$ kuwa ni busara kwa tatizo hili - maadili kutoka 0 hadi 7.

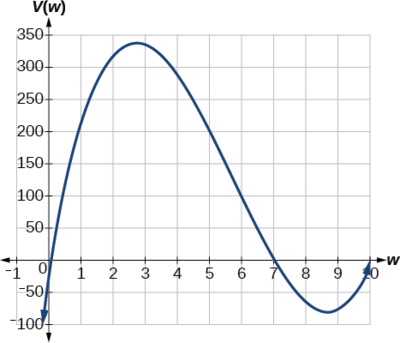
Grafu ya V (w) = (20-2w) (14-2w) w ambapo mhimili wa x umeandikwa w na mhimili wa y umeandikwa V (w). — Kielelezo$\PageIndex{24}$: Grafu ya$V(w)=(20-2w)(14-2w)w$

Kutoka kwenye grafu hii, tunageuka lengo letu kwa sehemu tu kwenye uwanja unaofaa,$[0, 7]$. Tunaweza kukadiria thamani ya juu kuwa karibu 340 cm za ujazo, ambayo hutokea wakati mraba ni karibu 2.75 cm kila upande. Ili kuboresha makadirio haya, tunaweza kutumia vipengele vya juu vya teknolojia yetu, ikiwa inapatikana, au tu kubadilisha dirisha letu ili kukuza kwenye grafu yetu ili kuzalisha Kielelezo$\PageIndex{25}$.

Grafu ya V (w) = (20-2w) (14-2w) w ambapo x-axis inaitwa w na mhimili wa y ni kinachoitwa V (w) kwenye uwanja [2.4, 3]. — Kielelezo$\PageIndex{25}$: Grafu ya$V(w)=(20-2w)(14-2w)w$.

Kutokana na mtazamo huu uliozunguka, tunaweza kuboresha makadirio yetu kwa kiasi cha juu hadi cm 339 za ujazo, wakati mraba hupima takriban 2.7 cm kila upande.

Zoezi$\PageIndex{1}$

Tumia teknolojia ili kupata maadili ya juu na ya chini wakati$[−1,4]$ wa kazi$f(x)=−0.2(x−2)^3(x+1)^2(x−4)$.

Jibu: Kima cha chini hutokea kwa takriban hatua$(0,−6.5)$,
na upeo hutokea kwa takriban hatua$(3.5,7)$.

Dhana muhimu

Kazi nyingi za shahada ya 2 au zaidi ni kazi laini, zinazoendelea.
Ili kupata zero za kazi ya polynomial, ikiwa inaweza kuzingatiwa, fanya kazi na kuweka kila sababu sawa na sifuri.
Njia nyingine ya kupata x-intercepts ya kazi polynomial ni grafu kazi na kutambua pointi ambazo grafu huvuka x-axis.
Uingizaji wa sifuri huamua jinsi grafu inavyofanya katika x-intercepts.
Grafu ya polynomial itavuka mhimili usio na usawa kwenye sifuri na wingi usio wa kawaida.
Grafu ya polynomial itagusa mhimili usio na usawa kwenye sifuri na hata wingi.
Tabia ya mwisho ya kazi ya polynomial inategemea muda unaoongoza.
Grafu ya kazi ya polynomial inabadilisha mwelekeo katika pointi zake za kugeuka.
Kazi ya polynomial ya shahada$n$ ina pointi nyingi za$n−1$ kugeuka.
Ili kuchora kazi za polynomial, pata zero na kuzidisha kwao, tambua tabia ya mwisho, na uhakikishe kuwa grafu ya mwisho ina pointi nyingi za$n−1$ kugeuka.
Kuchora kazi ya polynomial husaidia kukadiria extremas ya ndani na ya kimataifa.
Theorem ya Thamani ya Kati inatuambia kwamba ikiwa$f(a)$ na$f(b)$ kuwa na ishara tofauti, basi kuna angalau thamani moja$c$ kati$a$ na$b$ ambayo$f(c)=0$.

faharasa

kimataifa upeo
juu kugeuka uhakika juu ya grafu;$f(a)$ ambapo$f(a){\geq}f(x)$ kwa ajili ya wote$x$.

kimataifa chini ya
chini kugeuka uhakika juu ya grafu;$f(a)$ ambapo$f(a){\leq}f(x)$ kwa ajili ya wote$x$.

Theorem
ya Thamani ya Kati kwa namba mbili$a$ na$b$ katika uwanja wa$f$$f(a){\neq}f(b)$, ikiwa$a<b$ na, basi kazi inachukua kila thamani kati$f(a)$ na$f(b)$; hasa, wakati kazi ya polynomial inabadilika kutoka thamani hasi kwa thamani nzuri, kazi inapaswa kuvuka x-axis

kuzidisha idadi
ya mara sababu iliyotolewa inaonekana katika fomu iliyosababishwa ya equation ya polynomial; ikiwa polynomial ina sababu ya fomu$(x−h)^p$,$x=h$ ni sifuri ya wingi$p$.

Jedwali\(\PageIndex{2}\)
\(x\)	1	2	3	4
\(f(x)\)	5	0	-3	2