3.8: Inverses na Kazi kubwa

Last updated
Save as PDF

Page ID: 181247

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Katika sehemu hii, utakuwa:

Pata inverse ya kazi isiyo na nguvu ya polynomial.
Weka kikoa ili kupata inverse ya kazi ya polynomial.

Kipande cha changarawe kina sura ya koni na urefu sawa na radius mara mbili.

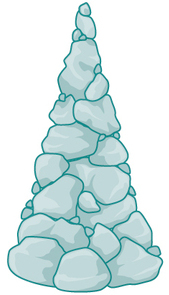
Gravel katika sura ya koni. — Kielelezo\(\PageIndex{1}\)

Kiasi kinapatikana kwa kutumia formula kutoka jiometri ya msingi.

\[ \begin{align*} V&=\dfrac{1}{3}\pi r^2h \\[4pt] &=\dfrac{1}{3}\pi r^2(2r)\\[4pt] &=\dfrac{2}{3}\pi r^3 \end{align*}\]

Tumeandika kiasi\(V\) katika suala la radius\(r\). Hata hivyo, wakati mwingine, tunaweza kuanza na kiasi na tunataka kupata radius. Kwa mfano: mteja anununua 100 miguu ya ujazo ya changarawe kujenga koni sura mlima na urefu mara mbili radius. Je, ni radius na urefu wa koni mpya? Ili kujibu swali hili, tunatumia formula

\[r=\sqrt[3]{\dfrac{3V}{2\pi}} \nonumber\]

Kazi hii ni inverse ya formula\(V\) kwa suala la\(r\).

Katika sehemu hii, tutazingatia inverses ya kazi nyingi na za busara na hasa kazi kubwa tunayokutana katika mchakato.

Kutafuta Inverse ya Kazi ya Polynomial

Kazi mbili\(f\) na\(g\) ni kazi inverse kama kwa kila jozi kuratibu katika\(f\)\((a,b)\), kuna sambamba kuratibu jozi katika kazi inverse,\(g\),\((b, a)\). Kwa maneno mengine, jozi za kuratibu za kazi za inverse zina pembejeo na pato zimebadilishana. Kazi moja kwa moja tu ina inverses. Kumbuka kwamba kazi moja kwa moja ina thamani ya pekee ya pato kwa kila thamani ya pembejeo na hupita mtihani wa mstari usio na usawa.

Kwa mfano, tuseme mtoza wa maji ya maji hujengwa kwa sura ya mto wa parabolic kama inavyoonekana kwenye Kielelezo\(\PageIndex{2}\). Tunaweza kutumia habari katika takwimu ili kupata eneo la uso wa maji ndani ya mto kama kazi ya kina cha maji.

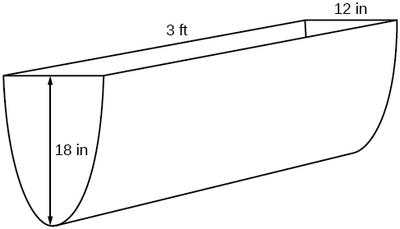
Mchoro wa kupitia nyimbo ya parabolic yaani 18 “kwa urefu, 3' urefu, na 12" kwa upana. — Kielelezo\(\PageIndex{2}\)

Kwa sababu itakuwa na manufaa kuwa na equation kwa sura parabolic msalaba-Sectional, sisi kulazimisha mfumo kuratibu katika sehemu ya msalaba, na\(x\)\(y\) kipimo usawa na kipimo wima, na asili katika vertex ya parabola (Kielelezo\(\PageIndex{3}\)).

Grafu ya parabola. — Kielelezo\(\PageIndex{3}\)

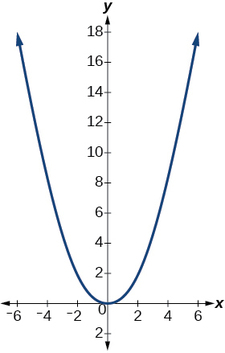
Kutoka hili tunapata equation kwa sura ya parabolic. Sisi kuwekwa asili katika vertex ya parabola, hivyo tunajua equation itakuwa na fomu\(y(x)=ax^2\). Equation yetu itahitaji kupitisha hatua\((6, 18)\), ambayo tunaweza kutatua kwa sababu ya kunyoosha\(a\).

\[ \begin{align*} 18&=a6^2 \\[4pt] a &=\dfrac{18}{36} \\[4pt] &=\dfrac{1}{2} \end{align*}\]

Sehemu yetu ya msalaba wa parabolic ina equation

\(y(x)=\dfrac{1}{2}x^2\)

Tunavutiwa na eneo la uso wa maji, kwa hiyo tunapaswa kuamua upana juu ya maji kama kazi ya kina cha maji. Kwa kina chochote\(y\), upana utapewa na\(2x\), kwa hiyo tunahitaji kutatua equation hapo juu\(x\) na kupata kazi inverse. Hata hivyo, angalia kwamba kazi ya awali sio moja kwa moja, na kwa kweli, kutokana na pato lolote kuna pembejeo mbili zinazozalisha pato sawa, moja chanya na moja hasi.

Ili kupata inverse, tunaweza kuzuia kazi yetu ya awali kwenye uwanja mdogo ambao ni moja kwa moja. Katika kesi hiyo, ni busara kujizuia\(x\) maadili mazuri. Kwenye uwanja huu, tunaweza kupata inverse kwa kutatua kwa kutofautiana kwa pembejeo:

\[ \begin{align*} y&=\dfrac{1}{2}x^2 \\[4pt] 2y&=x^2 \\[4pt] x&=\pm \sqrt{2y} \end{align*}\]

Hii si kazi kama ilivyoandikwa. Sisi ni kikwazo wenyewe kwa\(x\) maadili chanya, hivyo sisi kuondoa ufumbuzi hasi, kutupa kazi inverse sisi ni kuangalia kwa.

\(y=\dfrac{x^2}{2}\),\(x>0\)

Kwa sababu\(x\) ni umbali kutoka katikati ya parabola kwa upande wowote, upana mzima wa maji hapo juu utakuwa\(2x\). Mto huo ni miguu 3 (inchi 36) kwa muda mrefu, hivyo eneo la uso litakuwa:

\[ \begin{align*} \text{Area} &=l⋅w \\[4pt] &=36⋅2x \\[4pt] &=72x \\[4pt] &=72\sqrt{2y} \end{align*}\]

Mfano huu unaeleza pointi mbili muhimu:

Tunapopata inverse ya quadratic, tunapaswa kujizuia kwenye uwanja ambao kazi hiyo ni moja kwa moja.
Inverse ya kazi ya quadratic ni kazi ya mizizi ya mraba. Wote ni kazi za toolkit na aina tofauti za kazi za nguvu.

Kazi zinazohusisha mizizi mara nyingi huitwa kazi kubwa. Ingawa haiwezekani kupata inverse ya kazi nyingi za polynomial, baadhi ya polynomials ya msingi yana inverses. Kazi hizo huitwa kazi zisizoweza kuingizwa, na tunatumia notation\(f^{−1}(x)\).

\(f^{−1}(x)\)Onyo: si sawa na usawa wa kazi\(f(x)\). Matumizi haya ya “—1" yamehifadhiwa ili kuashiria kazi za inverse. Ili kutaja usawa wa kazi\(f(x)\), tunahitaji kuandika:

\[ (f(x))^{−1}=\frac{1}{f(x)}.\]

Uhusiano muhimu kati ya kazi za kinyume ni kwamba “hutenganisha” kila mmoja. Ikiwa\(f^{−1}\) ni inverse ya kazi\(f\), basi\(f\) ni inverse ya kazi\(f^{−1}\). Kwa maneno mengine, chochote kazi\(f\) gani kwa\(x\),\(f^{−1}\) undoes ni - na kinyume chake.

\(f^{−1}(f(x))=x\), kwa wote\(x\) katika uwanja wa\(f\)

\(f(f^{−1}(x))=x\), kwa wote\(x\) katika uwanja wa\(f^{−1}\)

Kumbuka kuwa inverse inachukua kikoa na aina mbalimbali ya kazi ya awali.

KUTHIBITISHA KAZI MBILI NI INVERSES YA MTU MWINGINE

Kazi mbili,\(f\) na\(g\), ni inverses ya mtu mwingine kama kwa wote\(x\) katika uwanja wa\(f\) na\(g\),

\(g(f(x))=f(g(x))=x\)

Howto: Kutokana na kazi ya polynomial, tafuta inverse ya kazi kwa kuzuia kikoa kwa namna ambayo kazi mpya ni moja kwa moja

Badilisha nafasi\(f(x)\) na\(y\).
\(x\)Kubadilishana na\(y\).
Kutatua kwa\(y\), na rename kazi\(f^{−1}(x)\).

Mfano\(\PageIndex{1}\): Verifying Inverse Functions

Onyesha kwamba\(f(x)=\frac{1}{x+1}\) na\(f^{−1}(x)=\frac{1}{x}−1\) ni inverses, kwa\(x≠0,−1\).

Suluhisho

Lazima tuonyeshe kwamba\(f^{−1}(f(x))=x\) na\(f(f^{−1}(x))=x\).

\[ \begin{align*} f^{−1}(f(x)) &=f^{−1}\left(\dfrac{1}{x+1}\right)\\[4pt] &=\dfrac{1}{\dfrac{1}{x+1}}−1\\[4pt] &=(x+1)−1\\[4pt] &=x\end{align*}\]

\[ \begin{align*} f(f^{−1}(x)) &=f(\dfrac{1}{x−1})\\[4pt] &=\dfrac{1}{\left(\dfrac{1}{x−1}\right)+1}\\[4pt] &=\dfrac{1}{\dfrac{1}{x}}\\[4pt] &=x\end{align*}\]

Kwa hiyo,\(f(x)=\dfrac{1}{x+1}\) na\(f^{−1}(x)=\dfrac{1}{x}−1\) ni inverses.

Zoezi\(\PageIndex{1}\)

Onyesha kwamba\(f(x)=\frac{x+5}{3}\) na\(f^{−1}(x)=3x−5\) ni inverses.

Jibu: \(f^{−1}(f(x))=f^{−1}(\frac{x+5}{3})=3(\frac{x+5}{3})−5=(x−5)+5=x\)
Jibu b: \(f(f^{−1}(x))=f(3x−5)=\frac{(3x−5)+5}{3}=\frac{3x}{3}=x\)

Mfano\(\PageIndex{2}\): Finding the Inverse of a Cubic Function

Pata inverse ya kazi\(f(x)=5x^3+1\).

Suluhisho

Hii ni mabadiliko ya kazi ya msingi ya vifaa vya ujazo, na kulingana na ujuzi wetu wa kazi hiyo, tunajua ni moja kwa moja. Kutatua kwa inverse kwa kutatua\(x\).

\(y=5x^3+1\)

\(x=5y^3+1\)

\(x−1=5y^3\)

\(\dfrac{x−1}{5}=y^3\)

\(f^{−1}(x)=\sqrt[3]{\dfrac{x−1}{5}}\)

Uchambuzi

Angalia grafu ya\(f\) na\(f^{–1}\). Angalia kwamba grafu moja ni mfano wa mwingine kuhusu mstari\(y=x\). Hii daima ni kesi wakati wa kuchora kazi na kazi yake inverse.

Pia, tangu njia hiyo ilihusisha kubadilishana\(x\) na\(y\), angalia pointi zinazofanana. Kama\((a,b)\) ni juu ya grafu ya\(f\), basi\((b,a)\) ni juu ya grafu ya\(f^{–1}\). Kwa kuwa\((0,1)\) ni juu ya grafu ya\(f\), basi\((1,0)\) ni juu ya grafu ya\(f^{–1}\). Vile vile, tangu\((1,6)\) ni kwenye grafu ya\(f\), basi\((6,1)\) ni kwenye grafu ya\(f^{–1}\) (Kielelezo\(\PageIndex{9}\)).

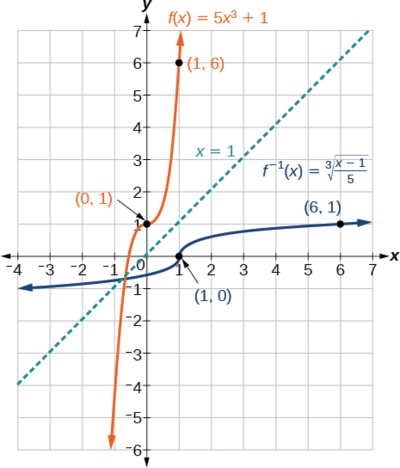
Grafu ya f (x) =5x^ 3+1 na inverse yake, f^ (-1) (x) =3sqrt ((x-1)/(5)). — Kielelezo\(\PageIndex{4}\)

Zoezi\(\PageIndex{2}\)

Kupata kazi inverse ya\(f(x)=\sqrt[3]{x+4}\).

Jibu: \(f^{−1}(x)=x^3−4\)

Kuzuia Domain Kupata Inverse ya Kazi Polynomial

Hadi sasa, tumeweza kupata kazi za inverse za kazi za ujazo bila ya kuzuia vikoa vyao. Hata hivyo, kama tunavyojua, sio polynomials zote za ujazo ni moja kwa moja. Baadhi ya kazi ambazo si moja kwa moja zinaweza kuwa na kikoa chao kizuizi ili wawe moja kwa moja, lakini tu juu ya uwanja huo. Kazi juu ya kikoa kilichozuiliwa ingekuwa na kazi ya inverse. Kwa kuwa kazi za quadratic sio moja kwa moja, tunapaswa kuzuia uwanja wao ili kupata inverses yao.

KUZUIA KIKOA

Ikiwa kazi si moja kwa moja, haiwezi kuwa na inverse. Kama sisi kuzuia uwanja wa kazi ili inakuwa moja kwa moja, hivyo kujenga kazi mpya, kazi hii mpya itakuwa na inverse.

Jinsi ya: Kutokana na kazi ya polynomial, kuzuia uwanja wa kazi ambayo si moja kwa moja na kisha kupata inverse

Kuzuia kikoa kwa kuamua uwanja ambao kazi ya awali ni moja kwa moja.
Badilisha nafasi\(f(x)\) na\(y\).
\(x\)Kubadilishana na\(y\).
Kutatua kwa\(y\), na kubadili jina kazi au jozi ya kazi\(f^{−1}(x)\).
Tathmini formula\(f^{−1}(x)\) kwa kuhakikisha kwamba matokeo ya kazi inverse yanahusiana na uwanja vikwazo wa kazi ya awali.

Mfano\(\PageIndex{3}\): Restricting the Domain to Find the Inverse of a Polynomial Function

Kupata kazi inverse ya\(f\):

\(f(x)={(x−4)}^2\),\(x≥4\)
\(f(x)={(x−4)}^2\),\(x≤4\)

Suluhisho

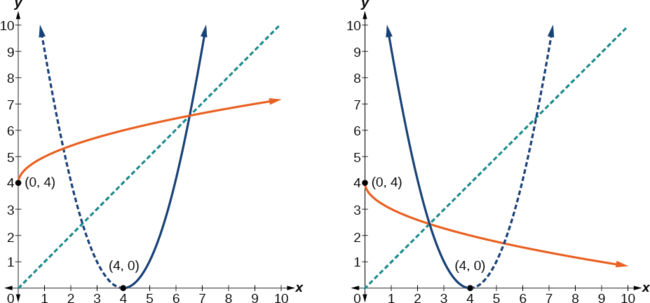
Kazi ya awali\(f(x)={(x−4)}^2\) sio moja kwa moja, lakini kazi imezuiwa\(x≤4\) kwenye uwanja wa\(x≥4\) au ambayo ni moja kwa moja (Kielelezo\(\PageIndex{6}\)).

Grafu mbili za f (x) = (x-4) ^2 ambapo kwanza ni wakati x — Kielelezo\(\PageIndex{5}\)

Ili kupata inverse, kuanza kwa kuchukua nafasi\(f(x)\) na kutofautiana rahisi\(y\).

\(y={(x−4)}^2\)\(x\)Kubadilishana na\(y\).

\(x={(y−4)}^2\)Chukua mizizi ya mraba.

\(\pm \sqrt{x}=y−4\)\(4\)Ongeza pande zote mbili.

\(4\pm \sqrt{x} =y\)

Hii si kazi kama ilivyoandikwa. Tunahitaji kuchunguza vikwazo kwenye uwanja wa kazi ya awali ili kuamua inverse. Kwa kuwa tulibadilisha majukumu ya\(x\) na\(y\) kwa asili\(f(x)\), tuliangalia uwanja: maadili\(x\) yanaweza kudhani. Wakati sisi kuachwa majukumu ya\(x\) na\(y\), hii alitupa maadili\(y\) inaweza kudhani. Kwa kazi hii,\(x≥4\), hivyo kwa inverse, tunapaswa kuwa\(y≥4\), ambayo ni nini kazi yetu inverse anatoa.

Uwanja wa kazi ya awali ulizuiliwa\(x≥4\), hivyo matokeo ya inverse yanahitaji kuwa sawa\(f(x)≥4\), na tunapaswa kutumia kesi +:
\(f^{−1}(x)=4+\sqrt{x}\)
uwanja wa kazi ya awali ilikuwa vikwazo kwa\(x≤4\), hivyo matokeo ya inverse haja ya kuwa sawa,\(f(x)≤4\), na ni lazima kutumia — kesi:
\(f^{−1}(x)=4−\sqrt{x}\)

Uchambuzi

Katika grafu katika Kielelezo\(\PageIndex{6}\), tunaona kazi ya awali iliyowekwa kwenye seti sawa ya shaba kama kazi yake ya inverse. Angalia kwamba pamoja grafu zinaonyesha ulinganifu kuhusu mstari\(y=x\). jozi kuratibu\((4,0)\) ni juu ya grafu off f na jozi kuratibu\((0, 4)\) ni juu ya grafu ya\(f^{−1}\). Kwa jozi yoyote kuratibu, kama\((a, b)\) ni juu ya grafu ya\(f\), basi\((b, a)\) ni juu ya grafu ya\(f^{−1}\). Hatimaye, angalia kwamba grafu ya\(f\) intersects grafu ya\(f^{−1}\) juu ya mstari\(y=x\). Pointi ya makutano kwa grafu ya\(f\) na\(f^{−1}\) daima uongo juu ya mstari\(y=x\).

Grafu mbili za kazi ya parabolic na nusu ya inverse yake. — Kielelezo\(\PageIndex{6}\)

Mfano\(\PageIndex{4}\): Finding the Inverse of a Quadratic Function When the Restriction Is Not Specified

Kuzuia uwanja na kisha kupata inverse ya

\(f(x)={(x−2)}^2−3\).

Suluhisho

Tunaweza kuona hii ni parabola na kipeo katika\((2,–3)\) kwamba kufungua zaidi. Kwa sababu grafu itapungua kwa upande mmoja wa kipeo na kuongezeka kwa upande mwingine, tunaweza kuzuia kazi hii kwenye uwanja ambao utakuwa moja kwa moja kwa kupunguza kikoa\(x≥2\).

Ili kupata inverse, tutatumia fomu ya vertex ya quadratic. Tunaanza\(f(x)\) kwa kuchukua nafasi ya kutofautiana rahisi\(y\), kisha tatua\(x\).

\(y={(x−2)}^2−3\)\(x\)Kubadilishana na\(y\).

\(x={(y−2)}^2−3\)Ongeza 3 kwa pande zote mbili.

\(x+3={(y−2)}^2\)Chukua mizizi ya mraba.

\(\pm \sqrt{x+3}=y−2\)Ongeza 2 kwa pande zote mbili.

\(2\pm \sqrt{x+3}=y\)Badilisha jina kazi.

\(f^{−1}(x)=2\pm \sqrt{x+3}\)

Sasa tunahitaji kuamua kesi ipi ya kutumia. Kwa sababu sisi vikwazo kazi yetu ya awali kwa uwanja wa\(x≥2\), matokeo ya inverse lazima sawa, kutuambia kutumia kesi +

\(f^{−1}(x)=2+\sqrt{x+3}\)

Ikiwa quadratic haikupewa katika fomu ya kipeo, kuandika tena katika fomu ya vertex ingekuwa hatua ya kwanza. Kwa njia hii tunaweza kuchunguza kwa urahisi kuratibu za vertex ili kutusaidia kuzuia kikoa.

Uchambuzi

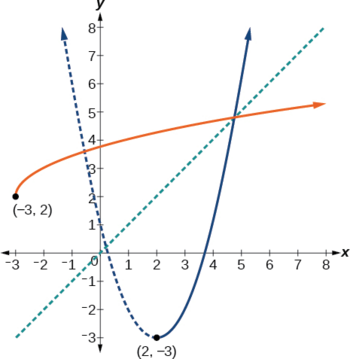
Kumbuka kwamba sisi kiholela aliamua kuzuia uwanja juu\(x≥2\). Tunaweza tu kwa urahisi wameamua kuzuia uwanja kwa\(x≤2\), katika kesi hiyo\(f^{−1}(x)=2−\sqrt{x+3}\). Kuzingatia kazi ya awali iliyowekwa kwenye seti moja ya shoka kama kazi yake inverse katika Kielelezo\(\PageIndex{7}\). Angalia kwamba grafu zote zinaonyesha ulinganifu kuhusu mstari\(y=x\). jozi kuratibu\((2, −3)\) ni juu ya grafu ya\(f\) na jozi kuratibu\((−3, 2)\) ni juu ya grafu ya\(f^{−1}\). Kuzingatia kutoka kwenye grafu ya kazi zote mbili kwenye seti moja ya shaba

uwanja wa\(f=\) aina mbalimbali\(f^{–1}=[2,\infty)\)

uwanja wa\(f^{–1}=\) aina mbalimbali ya\(f=[–3,\infty)\).

Hatimaye, angalia kwamba grafu ya\(f\) intersects grafu ya\(f^{−1}\) kando ya mstari\(y=x\).

Grafu ya kazi ya parabolic na nusu ya inverse yake. — Kielelezo\(\PageIndex{7}\)

Zoezi\(\PageIndex{4}\)

Pata inverse ya kazi\(f(x)=x^2+1\), kwenye kikoa\(x≥0\).

Jibu: \(f^{−1}(x)=\sqrt{x−1}\)

Kupata Inverses

Angalia kwamba kazi kutoka kwa mifano ya awali zilikuwa zote za polynomials, na inverses zao zilikuwa kazi kubwa. Ikiwa tunataka kupata inverse ya kazi kubwa, tutahitaji kuzuia uwanja wa jibu kwa sababu kazi ya awali ni mdogo.

Jinsi ya: Kutokana na kazi kubwa, tafuta inverse

Tambua aina mbalimbali za kazi ya awali.
Badilisha nafasi\(f(x)\) na\(y\), kisha tatua\(x\).
Ikiwa ni lazima, punguza kikoa cha kazi ya inverse kwa aina mbalimbali ya kazi ya awali.

Mfano\(\PageIndex{5}\): Finding the Inverse of a Radical Function

Kuzuia uwanja wa kazi\(f(x)=\sqrt{x−4}\) na kisha kupata inverse.

Suluhisho

Kumbuka kuwa kazi ya awali ina mbalimbali\(f(x)≥0\). Badilisha nafasi\(f(x)\) na\(y\), kisha tatua\(x\).

\(y=\sqrt{x−4}\)Badilisha nafasi\(f(x)\) na\(y\).

\(x=\sqrt{y−4}\)\(x\)Kubadilishana na\(y\).

\(x=\sqrt{y−4}\)Mraba kila upande.

\(x^2=y−4\)Ongeza 4.

\(x^2+4=y\)Badilisha jina kazi\(f^{−1}(x)\).

\(f^{−1}(x)=x^2+4\)

Kumbuka kwamba uwanja wa kazi hii lazima iwe mdogo kwa kazi mbalimbali ya awali.

\(f^{−1}(x)=x^2+4\),\(x≥0\)

Uchambuzi

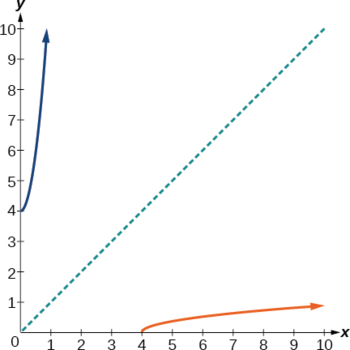
Taarifa katika Kielelezo\(\PageIndex{8}\) kwamba inverse ni reflection ya kazi ya awali juu ya mstari\(y=x\). Kwa sababu kazi ya awali ina matokeo mazuri tu, kazi ya inverse ina pembejeo zisizo za negative tu.

Grafu ya f (x) =sqrt (x-4) na inverse yake, f^ (-1) (x) =x ^ 2+4. — Kielelezo\(\PageIndex{8}\)

Zoezi\(\PageIndex{5}\)

Kuzuia kikoa na kisha kupata inverse ya kazi\(f(x)=\sqrt{2x+3}\).

Jibu: \(f^{−1}(x)=\frac{x^2−3}{2}\),\(x≥0\)

Kutatua Matumizi ya Kazi za Radical

Kazi kubwa ni ya kawaida katika mifano ya kimwili, kama tulivyoona katika kopo ya sehemu. Sasa tuna zana za kutosha ili tuweze kutatua tatizo lililofanywa mwanzoni mwa sehemu hiyo.

Mfano\(\PageIndex{6}\): Solving an Application with a Cubic Function

Kipande cha changarawe kina sura ya koni na urefu sawa na radius mara mbili. Kiasi cha koni katika suala la radius hutolewa na

\[V=\dfrac{2}{3}\pi r^3 \nonumber\]

Pata inverse ya kazi\(V=\frac{2}{3}\pi r^3\) ambayo huamua kiasi\(V\) cha koni na ni kazi ya radius\(r\). Kisha utumie kazi ya inverse ili kuhesabu radius ya kilima hicho cha changarawe kupima miguu 100 ya ujazo. Tumia\(\pi=3.14\).

Suluhisho

Anza na kazi iliyotolewa kwa\(V\). Kumbuka kwamba uwanja maana kwa ajili ya kazi ni\(r>0\) tangu radii hasi bila mantiki katika muktadha huu wala bila radius ya\(0\). Pia angalia aina mbalimbali za kazi (kwa hiyo, uwanja wa kazi ya inverse) ni\(V>0\). Tatua\(r\) kwa suala la\(V\), kwa kutumia njia iliyoelezwa hapo awali. Kumbuka kuwa katika programu halisi ya ulimwengu, hatuwezi kubadili vigezo wakati wa kutafuta inverses. Badala yake, sisi mabadiliko ambayo variable ni kuchukuliwa kuwa variable huru.

\[ V =\dfrac{2}{3}\pi r^3\nonumber \]

Kutatua kwa\(r^3\).

\[r^3 =\dfrac{3V}{2\pi} \nonumber\]

Kutatua kwa\(r\).

\[ r=\sqrt[3]{\dfrac{3V}{2\pi}} \nonumber \]

Hii ni matokeo yaliyotajwa katika kopo ya sehemu. Sasa tathmini hii kwa\(V=100\) na\(\pi=3.14\).

\[ \begin{align*} r&=\sqrt[3]{\dfrac{3V}{2\pi}} \\[4pt] &=\sqrt[3]{\dfrac{3⋅100}{2⋅3.14}} \\[4pt] &≈\sqrt[3]{47.7707} \\[4pt] &≈3.63 \end{align*}\]

Kwa hiyo, radius ni karibu 3.63 ft.

Kuamua Domain ya Kazi ya Radical Imejumuishwa na Kazi Zingine

Wakati kazi kubwa zinajumuisha kazi nyingine, kuamua uwanja unaweza kuwa ngumu zaidi.

Mfano\(\PageIndex{7}\): Finding the Domain of a Radical Function Composed with a Rational Function

Pata uwanja wa kazi:

\[f(x)=\sqrt{\frac{(x+2)(x−3)}{(x−1)}}. \nonumber\]

Suluhisho

Kwa sababu mizizi ya mraba inaelezwa tu wakati wingi chini ya radical sio hasi, tunahitaji kuamua wapi

\[\frac{(x+2)(x−3)}{(x−1)}≥0. \nonumber\]

Pato la kazi ya busara inaweza kubadilisha ishara (mabadiliko kutoka kwa chanya hadi hasi au kinyume chake) katika x -intercepts na kwa asymptotes wima. Kwa equation hii, grafu inaweza kubadilisha ishara katika\(x=–2\),\(1\), na\(3\).

Kuamua vipindi ambavyo kujieleza kwa busara ni chanya, tunaweza kupima maadili fulani katika kujieleza au kuchora grafu. Wakati mbinu zote mbili zinafanya kazi vizuri, kwa mfano huu tutatumia grafu kama inavyoonekana kwenye Kielelezo\(\PageIndex{9}\).

Grafu ya kazi kubwa ambayo inaonyesha ambapo matokeo ni yasiyo ya negative. — Kielelezo\(\PageIndex{9}\)

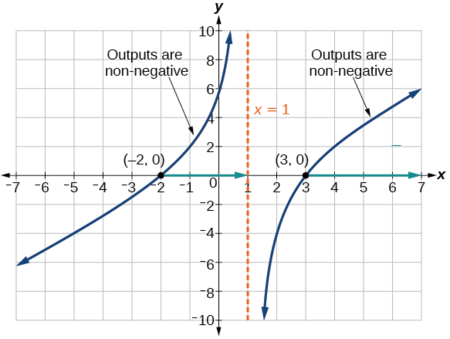
Kazi hii ina mbili x -intercepts, zote mbili ambazo zinaonyesha tabia linear karibu x -intercepts. Kuna asymptote moja ya wima, inayolingana na sababu ya mstari; tabia hii ni sawa na kazi ya msingi ya toolkit, na hakuna asymptote ya usawa kwa sababu kiwango cha nambari ni kubwa kuliko kiwango cha denominator. Kuna y -intercept at\((0,\sqrt{6})\).

Kutoka y -intercept na x -intercept saa\(x=−2\), tunaweza mchoro upande wa kushoto wa grafu. Kutoka kwa tabia katika asymptote, tunaweza kupiga upande wa kulia wa grafu.

Kutoka kwenye grafu, sasa tunaweza kusema juu ya vipindi vipi matokeo yatakuwa yasiyo ya hasi, ili tuweze kuwa na uhakika kwamba kazi ya awali\(f(x)\) itafafanuliwa. \(f(x)\)ina uwanja\(−2≤x<1\) au\(x≥3\), au katika nukuu ya muda,\([−2,1)∪[3,\infty)\).

Kutafuta Inverses ya Kazi za busara

Kama ilivyo kwa kutafuta inverses ya kazi za quadratic, wakati mwingine ni muhimu kupata inverse ya kazi ya busara, hasa ya kazi za busara ambazo ni uwiano wa kazi za mstari, kama vile katika maombi ya ukolezi.

Mfano\(\PageIndex{8}\): Finding the Inverse of a Rational Function

Kazi

\[\displaystyle C=\frac{20+0.4n}{100+n}\]

inawakilisha mkusanyiko\(C\) wa suluhisho la asidi baada ya\(n\) mL ya ufumbuzi wa 40% imeongezwa kwa 100 ml ya suluhisho la 20%. Kwanza, tafuta inverse ya kazi; yaani, kupata kujieleza\(n\) kwa suala la\(C\). Kisha utumie matokeo yako ili ueleze ni kiasi gani cha ufumbuzi wa 40% unapaswa kuongezwa ili mchanganyiko wa mwisho ni suluhisho la 35%.

Suluhisho

Sisi kwanza tunataka inverse ya kazi ili kuamua ngapi mL tunahitaji kwa mkusanyiko fulani. Tutatatua\(n\) kwa suala la\(C\).

\[ \begin{align*} C&=\dfrac{20+0.4n}{100+n} \\[4pt] C(100+n)&=20+0.4n\\[4pt] 100C+Cn&=20+0.4n\\[4pt] 100C−20&=0.4n−Cn\\[4pt] 100C−20&=(0.4−C)n\\[4pt] n&=\dfrac{100C−20}{0.4−C}\end{align*}\]

Sasa tathmini kazi hii kwa 35%, ambayo ni\(C=0.35\).

\[ \begin{align*} n&=\dfrac{100(0.35)−20}{0.4−0.35}\\[4pt] &=\dfrac{15}{0.05}\\[4pt] &=300\end{align*}\]

Tunaweza kuhitimisha kwamba 300 ml ya suluhisho la 40% inapaswa kuongezwa.

Zoezi\(\PageIndex{8}\)

Pata inverse ya kazi\(f(x)=\frac{x+3}{x−2}\).

Jibu: \(f^{−1}(x)=\frac{2x+3}{x−1}\)

vyombo vya habari

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na inverses na kazi kubwa.

Dhana muhimu

Inverse ya kazi ya quadratic ni kazi ya mizizi ya mraba.
Ikiwa\(f^{−1}\) ni inverse ya kazi\(f\), basi\(f\) ni inverse ya kazi\(f^{−1}\). Angalia Mfano\(\PageIndex{1}\).
Ingawa haiwezekani kupata inverse ya kazi nyingi za polynomial, baadhi ya polynomials ya msingi haiwezi kuingizwa. Angalia Mfano\(\PageIndex{2}\).
Ili kupata inverse ya kazi fulani, tunapaswa kuzuia kazi kwenye uwanja ambao utakuwa moja kwa moja. Angalia Mifano\(\PageIndex{3}\) na\(\PageIndex{4}\)
Tunapopata inverse ya kazi kubwa, tunahitaji kizuizi kwenye uwanja wa jibu. Angalia Mfano\(\PageIndex{5}\) na\(\PageIndex{7}\).
Inverse na radical na kazi inaweza kutumika kutatua matatizo ya maombi. Angalia Mifano\(\PageIndex{6}\) na\(\PageIndex{8}\).