3.2: Kazi za Quadratic

Last updated
Save as PDF

Page ID: 181281

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Tambua sifa za parabolas.
Kuelewa jinsi grafu ya parabola inahusiana na kazi yake ya quadratic.
Kuamua quadratic kazi ya chini au thamani ya kiwango cha juu.
Kutatua matatizo yanayohusisha quadratic kazi ya chini au thamani ya kiwango cha juu.

Curved Antena, kama vile wale inavyoonekana katika Kielelezo$\PageIndex{1}$, ni kawaida kutumika kwa lengo microwaves na mawimbi ya redio kusambaza televisheni na simu ishara, pamoja na satellite na spacecraft mawasiliano. Sehemu ya msalaba wa antenna iko katika sura ya parabola, ambayo inaweza kuelezewa na kazi ya quadratic.

$Satellite sahani.$

Kielelezo$\PageIndex{1}$: safu ya sahani satellite. (mikopo: Mathayo Colvin de Valle, Flickr)

Katika sehemu hii, sisi kuchunguza kazi quadratic, ambayo mara nyingi mfano matatizo kuwashirikisha eneo na projectile mwendo. Kufanya kazi na kazi za quadratic inaweza kuwa ngumu zaidi kuliko kufanya kazi na kazi za shahada ya juu, hivyo hutoa fursa nzuri kwa utafiti wa kina wa tabia ya kazi.

Kutambua Tabia za Parabolas

Grafu ya kazi ya quadratic ni safu ya U-umbo inayoitwa parabola. Kipengele kimoja muhimu cha grafu ni kwamba ina hatua kali, inayoitwa vertex. Ikiwa parabola inafungua, vertex inawakilisha hatua ya chini kabisa kwenye grafu, au thamani ya chini ya kazi ya quadratic. Ikiwa parabola inafungua, vertex inawakilisha hatua ya juu kwenye grafu, au thamani ya juu. Katika hali yoyote, vertex ni hatua ya kugeuka kwenye grafu. Grafu pia inalinganishwa na mstari wa wima inayotolewa kupitia vertex, inayoitwa mhimili wa ulinganifu. Makala haya ni mfano katika Kielelezo$\PageIndex{2}$.

alt — Kielelezo$\PageIndex{2}$: Grafu ya parabola kuonyesha ambapo$x$ na$y$ intercepts, kipeo, na mhimili wa ulinganifu ni.

Y-intercept ni hatua ambayo parabola huvuka$y$ -axis. Ya x-intercepts ni pointi ambazo parabola huvuka$x$ -axis. Ikiwa zipo, x-intercepts inawakilisha zero, au mizizi, ya kazi ya quadratic, maadili ambayo$y=0$.$x$

Mfano$\PageIndex{1}$: Identifying the Characteristics of a Parabola

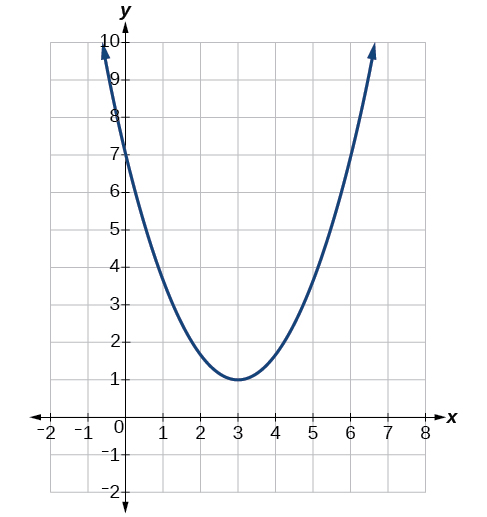
Kuamua vertex, mhimili wa ulinganifu, zero, na y-intercept ya parabola inavyoonekana katika Kielelezo$\PageIndex{3}$.

Grafu ya parabola yenye vertex saa (3, 1) na y-intercept saa (0, 7). — Kielelezo$\PageIndex{3}$.

Suluhisho

Vertex ni hatua ya kugeuka ya grafu. Tunaweza kuona kwamba kipeo ni saa$(3,1)$. Kwa sababu parabola hii inafungua juu, mhimili wa ulinganifu ni mstari wa wima unaozunguka parabola kwenye vertex. Hivyo mhimili wa ulinganifu ni$x=3$. Parabola hii haina msalaba wa x-axis, kwa hiyo haina zero. Inavuka$y$ -axis kwa$(0,7)$ hivyo hii ni y-intercept.

Kuelewa Jinsi Grafu za Parabolas zinahusiana na Kazi zao za Quadratic

Fomu ya jumla ya kazi ya quadratic inatoa kazi kwa fomu

\[f(x)=ax^2+bx+c\]

ambapo$a$,$b$, na$c$ ni idadi halisi na$a{\neq}0$. Ikiwa$a>0$, parabola inafungua juu. Ikiwa$a<0$, parabola inafungua chini. Tunaweza kutumia fomu ya jumla ya parabola ili kupata equation kwa mhimili wa ulinganifu.

Mhimili wa ulinganifu hufafanuliwa na$x=−\frac{b}{2a}$. Kama sisi kutumia formula quadratic$x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}$, kutatua$ax^2+bx+c=0$ kwa x-intercepts, au zero, tunapata thamani ya$x$ nusu kati yao ni daima$x=−\frac{b}{2a}$, equation kwa mhimili wa ulinganifu.

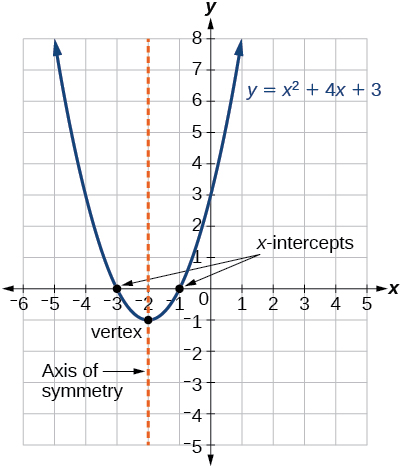
Kielelezo$\PageIndex{4}$ inawakilisha grafu ya kazi quadratic imeandikwa katika fomu ya jumla kama$y=x^2+4x+3$. Katika fomu hii,$a=1$,$b=4$, na$c=3$. Kwa sababu$a>0$, parabola inafungua juu. Mhimili wa ulinganifu ni$x=−\frac{4}{2(1)}=−2$. Hii pia ina maana kwa sababu tunaweza kuona kutoka kwenye grafu kwamba mstari wa wima$x=−2$ hugawanya grafu kwa nusu. Vertex daima hutokea kando ya mhimili wa ulinganifu. Kwa parabola inayofungua zaidi, kipeo hutokea kwa kiwango cha chini kabisa kwenye grafu, kwa mfano huu,$(−2,−1)$. The x-intercepts, pointi hizo ambapo parabola huvuka x-axis, hutokea$(−3,0)$ na$(−1,0)$.

Grafu ya parabola inayoonyesha ambapo x na y inakataza, vertex, na mhimili wa ulinganifu ni kwa kazi y=x ^ 2+4x+3. — Kielelezo$\PageIndex{4}$: Grafu ya parabola kuonyesha ambapo$x$ na$y$ intercepts, vertex, na mhimili wa ulinganifu ni kwa ajili ya kazi$y=x^2+4x+3$.

Fomu ya kawaida ya kazi ya quadratic inatoa kazi kwa fomu

\[f(x)=a(x−h)^2+k\]

$(h, k)$wapi vertex. Kwa sababu kipeo kinaonekana katika fomu ya kawaida ya kazi ya quadratic, fomu hii pia inajulikana kama aina ya kipeo cha kazi ya quadratic.

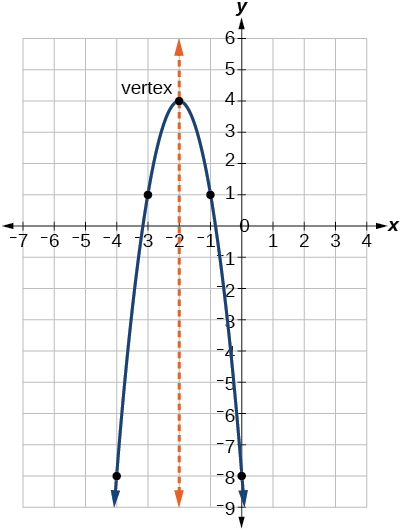
Kama ilivyo kwa fomu ya jumla, ikiwa$a>0$, parabola inafungua juu na vertex ni kiwango cha chini. Ikiwa$a<0$, parabola inafungua chini, na vertex ni kiwango cha juu. Kielelezo$\PageIndex{5}$ inawakilisha grafu ya kazi quadratic imeandikwa katika hali ya kawaida kama$y=−3(x+2)^2+4$. Kwa kuwa$x–h=x+2$ katika mfano huu,$h=–2$. Katika fomu hii,$a=−3$,$h=−2$, na$k=4$. Kwa sababu$a<0$, parabola inafungua chini. Vertex iko$(−2, 4)$.

Grafu ya parabola inayoonyesha ambapo x na y inakataza, kipeo, na mhimili wa ulinganifu ni kwa kazi y = -3 (x+2) ^2+4. — Kielelezo$\PageIndex{5}$: Grafu ya parabola kuonyesha ambapo$x$ na$y$ intercepts, vertex, na mhimili wa ulinganifu ni kwa ajili ya kazi$y=-3(x+2)^2+4$.

Fomu ya kawaida ni muhimu kwa kuamua jinsi grafu inabadilishwa kutoka kwenye grafu ya$y=x^2$. Kielelezo$\PageIndex{6}$ ni grafu ya kazi hii ya msingi.

Ikiwa$k>0$, grafu inabadilika zaidi, wakati ikiwa$k<0$, grafu inabadilika chini. Katika Kielelezo$\PageIndex{5}$$k>0$, hivyo grafu inabadilishwa vitengo 4 juu. Ikiwa$h>0$, grafu inabadilika kuelekea kulia na ikiwa$h<0$, grafu inabadilika upande wa kushoto. Katika Kielelezo$\PageIndex{5}$$h<0$, hivyo grafu inabadilishwa vitengo 2 upande wa kushoto. Ukubwa wa$a$ inaonyesha kunyoosha kwa grafu. Ikiwa$|a|>1$, hatua inayohusishwa na mabadiliko fulani ya thamani ya x-x mbali na mhimili wa x, hivyo grafu inaonekana kuwa nyembamba, na kuna kunyoosha wima. Lakini ikiwa$|a|<1$, hatua inayohusishwa na mabadiliko fulani ya thamani ya x karibu na x-axis, hivyo grafu inaonekana kuwa pana, lakini kwa kweli kuna compression wima. Katika Kielelezo$\PageIndex{5}$$|a|>1$, hivyo grafu inakuwa nyepesi.

Fomu ya kawaida na fomu ya jumla ni mbinu sawa za kuelezea kazi sawa. Tunaweza kuona hili kwa kupanua fomu ya jumla na kuiweka sawa na fomu ya kawaida.

\[\begin{align*} a(x−h)^2+k &= ax^2+bx+c \\[4pt] ax^2−2ahx+(ah^2+k)&=ax^2+bx+c \end{align*} \]

Kwa maneno ya mstari kuwa sawa, coefficients lazima iwe sawa.

\[–2ah=b \text{, so } h=−\dfrac{b}{2a}. \nonumber\]

Hii ni mhimili wa ulinganifu tuliyofafanua mapema. Kuweka maneno ya mara kwa mara sawa:

\[\begin{align*} ah^2+k&=c \\ k&=c−ah^2 \\ &=c−a\cdot\Big(-\dfrac{b}{2a}\Big)^2 \\ &=c−\dfrac{b^2}{4a} \end{align*}\]

Katika mazoezi, ingawa, kwa kawaida ni rahisi kukumbuka kwamba$k$ ni thamani ya pato ya kazi wakati pembejeo ni$h$, hivyo$f(h)=k$.

Ufafanuzi: Fomu za Kazi za Quadratic

Kazi ya quadratic ni kazi ya shahada mbili. Grafu ya kazi ya quadratic ni parabola.

Aina ya jumla ya kazi ya quadratic ni$f(x)=ax^2+bx+c$ wapi$a$$b$,, na$c$ ni namba halisi na$a{\neq}0$.
Fomu ya kawaida ya kazi ya quadratic ni$f(x)=a(x−h)^2+k$.
Vertex$(h,k)$ iko\[h=–\dfrac{b}{2a},\;k=f(h)=f(\dfrac{−b}{2a}).\]

HOWTO: Andika kazi ya quadratic kwa fomu ya jumla

Kutokana na grafu ya kazi ya quadratic, andika equation ya kazi kwa fomu ya jumla.

Tambua mabadiliko ya usawa ya parabola; thamani hii ni$h$. Tambua mabadiliko ya wima ya parabola; thamani hii ni$k$.
Weka maadili ya mabadiliko ya usawa na wima$h$ na$k$. katika kazi$f(x)=a(x–h)^2+k$.
Weka maadili ya hatua yoyote, isipokuwa vertex, kwenye grafu ya parabola kwa$x$ na$f(x)$.
Tatua kwa sababu ya kunyoosha,$|a|$.
Ikiwa parabola inafungua,$a>0$. Ikiwa parabola inafungua,$a<0$ kwani hii inamaanisha grafu ilionekana kuhusu x-axis.
Panua na kurahisisha kuandika kwa fomu ya jumla.

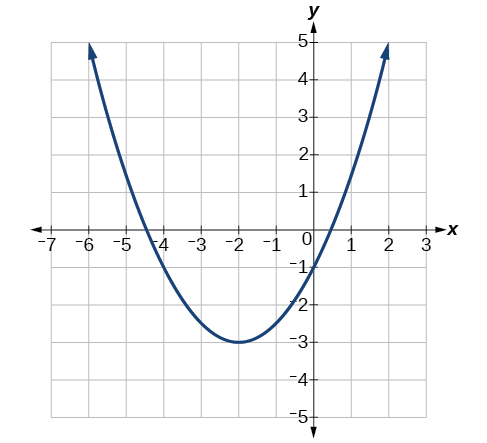
Mfano$\PageIndex{2}$: Writing the Equation of a Quadratic Function from the Graph

Andika equation kwa kazi quadratic$g$ katika Kielelezo$\PageIndex{7}$ kama mabadiliko ya$f(x)=x^2$, na kisha kupanua formula, na kurahisisha suala kuandika equation katika fomu ya jumla.

alt — Kielelezo$\PageIndex{7}$: Grafu ya parabola na vertex yake saa$(-2, -3)$.

Suluhisho

Tunaweza kuona grafu ya$g$ ni grafu ya$f(x)=x^2$ kubadilishwa kwa kushoto 2 na chini 3, kutoa formula katika fomu$g(x)=a(x+2)^2–3$.

Kubadilisha kuratibu za uhakika kwenye pembe, kama vile$(0,−1)$, tunaweza kutatua kwa sababu ya kunyoosha.

\[\begin{align} −1&=a(0+2)^2−3 \\ 2&=4a \\ a&=\dfrac{1}{2} \end{align}\]

Kwa fomu ya kawaida, mfano wa algebraic kwa grafu hii ni$g(x)=\dfrac{1}{2}(x+2)^2–3$.

Ili kuandika hii kwa fomu ya jumla ya polynomial, tunaweza kupanua formula na kurahisisha maneno.

\[\begin{align} g(x)&=\dfrac{1}{2}(x+2)^2−3 \\ &=\dfrac{1}{2}(x+2)(x+2)−3 \\ &=\dfrac{1}{2}(x^2+4x+4)−3 \\ &=\dfrac{1}{2}x^2+2x+2−3 \\ &=\dfrac{1}{2}x^2+2x−1 \end{align}\]

Angalia kwamba mabadiliko ya usawa na wima ya grafu ya msingi ya kazi ya quadratic huamua eneo la vertex ya parabola; vertex haiathiriwa na kunyoosha na compressions.

Uchambuzi

Tunaweza kuangalia kazi yetu kwa kutumia kipengele cha meza kwenye matumizi ya graphing. Ingiza kwanza$\mathrm{Y1=\dfrac{1}{2}(x+2)^2−3}$. Kisha, chagua$\mathrm{TBLSET}$, kisha utumie$\mathrm{TblStart=–6}$ na$\mathrm{ΔTbl = 2}$, na uchague$\mathrm{TABLE}$. Angalia Jedwali$\PageIndex{1}$

Jedwali$\PageIndex{1}$
$x$	-6	-4	-2	0	2
$y$	-5	-1	-3	-1	5

Jozi zilizoamriwa katika meza zinahusiana na pointi kwenye grafu.

Zoezi$\PageIndex{2}$

Gridi ya kuratibu imekuwa superimposed juu ya njia quadratic ya mpira wa kikapu katika Kielelezo$\PageIndex{8}$. Find equation kwa njia ya mpira. Je, shooter hufanya kikapu?

$alt$

Kielelezo$\PageIndex{8}$: Stop motioned picha ya mvulana kutupa mpira wa kikapu katika hoop kuonyesha Curve parabolic inafanya.
(mikopo: muundo wa kazi na Dan Meyer)

Jibu: Njia inapita kupitia asili na ina kipeo katika$(−4, 7)$, hivyo$h(x)=–\frac{7}{16}(x+4)^2+7$. Kufanya risasi,$h(−7.5)$ ingehitaji kuwa juu ya 4 lakini$h(–7.5){\approx}1.64$; yeye hana kufanya hivyo.

$alt$ Kutokana na kazi ya quadratic kwa fomu ya jumla, pata vertex ya parabola.

Tambua$a$,$b$, na$c$.
Pata$h$, kuratibu x-ya vertex, kwa kubadili$a$ na$b$ kuingia$h=–\frac{b}{2a}$.
Pata$k$, kuratibu y-ya vertex, kwa kutathmini$k=f(h)=f\Big(−\frac{b}{2a}\Big)$.

Mfano$\PageIndex{3}$: Finding the Vertex of a Quadratic Function

Pata vertex ya kazi ya quadratic$f(x)=2x^2–6x+7$. Andika upya quadratic katika fomu ya kawaida (fomu ya vertex).

Suluhisho

Kuratibu usawa wa vertex itakuwa

\[\begin{align} h&=–\dfrac{b}{2a} \\ &=-\dfrac{-6}{2(2)} \\ &=\dfrac{6}{4} \\ &=\dfrac{3}{2}\end{align}\]

Kuratibu wima ya vertex itakuwa

\[\begin{align} k&=f(h) \\ &=f\Big(\dfrac{3}{2}\Big) \\ &=2\Big(\dfrac{3}{2}\Big)^2−6\Big(\dfrac{3}{2}\Big)+7 \\ &=\dfrac{5}{2} \end{align}\]

Kuandika tena katika fomu ya kawaida, sababu ya kunyoosha itakuwa sawa na$a$ katika quadratic ya awali.

\[f(x)=ax^2+bx+c \\ f(x)=2x^2−6x+7\]

Kutumia vertex kuamua mabadiliko,

\[f(x)=2\Big(x–\dfrac{3}{2}\Big)^2+\dfrac{5}{2}\]

Uchambuzi

Sababu moja tunaweza kutaka kutambua kipeo cha parabola ni kwamba hatua hii itatujulisha nini thamani ya juu au ya chini ya kazi ni$(k)$, na ambapo hutokea,$(h)$.

Zoezi$\PageIndex{3}$

Kutokana na equation$g(x)=13+x^2−6x$, kuandika equation kwa fomu ya jumla na kisha katika fomu ya kawaida.

Jibu: $g(x)=x^2−6x+13$kwa fomu ya jumla;$g(x)=(x−3)^2+4$ kwa fomu ya kawaida.

Kutafuta Domain na Upeo wa Kazi ya Quadratic

Nambari yoyote inaweza kuwa thamani ya pembejeo ya kazi ya quadratic. Kwa hiyo, uwanja wa kazi yoyote ya quadratic ni namba zote halisi. Kwa sababu parabolas zina kiwango cha juu au kiwango cha chini, upeo umezuiwa. Kwa kuwa vertex ya parabola itakuwa ama kiwango cha juu au kiwango cha chini, upeo utakuwa na maadili yote ya y zaidi au sawa na y-kuratibu katika hatua ya kugeuka au chini ya au sawa na y-kuratibu katika hatua ya kugeuka, kulingana na kama parabola inafungua au chini.

Ufafanuzi: Domain na Upeo wa Kazi ya Quadratic

Kikoa cha kazi yoyote ya quadratic ni namba zote halisi.

Kazi ya quadratic iliyoandikwa kwa fomu ya jumla$f(x)=ax^2+bx+c$ na$a$ thamani nzuri ni$f(x){\geq}f ( −\frac{b}{2a}\Big)$, au$[ f(−\frac{b}{2a}),∞ ) $; aina ya kazi ya quadratic iliyoandikwa kwa fomu ya jumla na thamani hasi ni$f(x) \leq f(−\frac{b}{2a})$, au$(−∞,f(−\frac{b}{2a})]$.

Aina ya kazi ya quadratic iliyoandikwa kwa fomu ya kawaida$f(x)=a(x−h)^2+k$ na$a$ thamani nzuri ni aina mbalimbali$f(x) \geq k;$ ya kazi ya quadratic iliyoandikwa kwa fomu ya kawaida na$a$ thamani hasi ni$f(x) \leq k$.

$alt$ Kutokana na kazi ya quadratic, pata uwanja na upeo.

Tambua uwanja wa kazi yoyote ya quadratic kama namba zote halisi.
Kuamua ikiwa$a$ ni chanya au hasi. Ikiwa$a$ ni chanya, parabola ina kiwango cha chini. Ikiwa$a$ ni hasi, parabola ina kiwango cha juu.
Tambua thamani ya juu au ya chini ya parabola,$k$.
Ikiwa parabola ina kiwango cha chini, upeo hutolewa na$f(x){\geq}k$, au$\left[k,\infty\right)$. Ikiwa parabola ina kiwango cha juu, upeo hutolewa na$f(x){\leq}k$, au$\left(−\infty,k\right]$.

Mfano$\PageIndex{4}$: Finding the Domain and Range of a Quadratic Function

Kupata uwanja na aina mbalimbali ya$f(x)=−5x^2+9x−1$.

Suluhisho

Kama ilivyo na kazi yoyote ya quadratic, uwanja ni namba zote halisi.

Kwa sababu$a$ ni hasi, parabola inafungua chini na ina thamani ya juu. Tunahitaji kuamua thamani ya juu. Tunaweza kuanza kwa kutafuta x-thamani ya vertex.

\[\begin{align} h&=−\dfrac{b}{2a} \\ &=−\dfrac{9}{2(-5)} \\ &=\dfrac{9}{10} \end{align}\]

Thamani ya juu hutolewa na$f(h)$.

\[\begin{align} f(\dfrac{9}{10})&=5(\dfrac{9}{10})^2+9(\dfrac{9}{10})-1 \\&= \dfrac{61}{20}\end{align}\]

Aina ni$f(x){\leq}\frac{61}{20}$, au$\left(−\infty,\frac{61}{20}\right]$.

Zoezi$\PageIndex{4}$

Kupata uwanja na aina mbalimbali ya$f(x)=2\Big(x−\frac{4}{7}\Big)^2+\frac{8}{11}$.

Jibu: Kikoa ni namba zote halisi. Aina ni$f(x){\geq}\frac{8}{11}$, au$\left[\frac{8}{11},\infty\right)$.

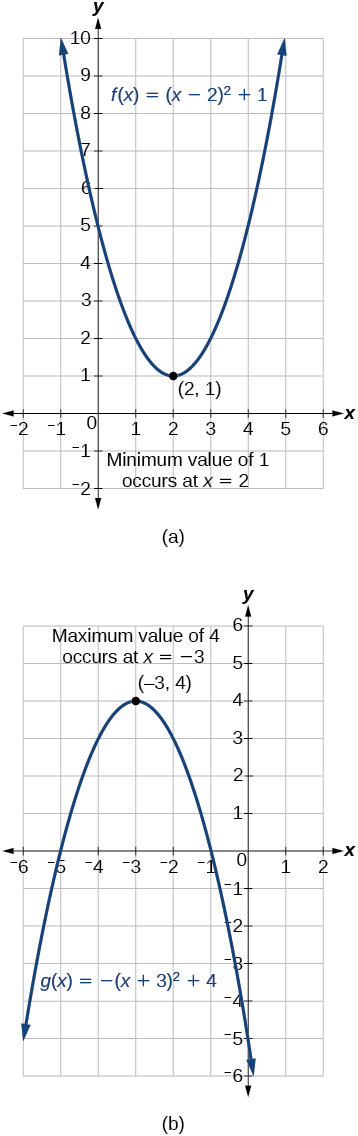
Kuamua Maadili ya Juu na ya chini ya Kazi za Quadratic

Pato la kazi ya quadratic kwenye vertex ni thamani ya juu au ya chini ya kazi, kulingana na mwelekeo wa parabola. Tunaweza kuona maadili ya kiwango cha juu na cha chini katika Kielelezo$\PageIndex{9}$.

Grafu mbili ambapo grafu ya kwanza inaonyesha thamani ya juu ya f (x) = (x-2) ^2+1 ambayo hutokea katika (2, 1) na grafu ya pili inaonyesha thamani ya chini ya g (x) =- (x+3) ^2+4 ambayo hutokea katika (-3, 4). — Kielelezo$\PageIndex{9}$: Kiwango cha chini na cha juu cha kazi mbili za quadratic.

Kuna matukio mengi ya ulimwengu halisi ambayo yanahusisha kutafuta thamani ya juu au ya chini ya kazi ya quadratic, kama vile programu zinazohusisha eneo na mapato.

Mfano$\PageIndex{5}$: Finding the Maximum Value of a Quadratic Function

Mkulima wa mashamba anataka kufungia nafasi ya mstatili kwa bustani mpya ndani ya mashamba yake yenye maboma. Amenunua futi 80 za uzio wa waya ili kuzunguka pande tatu, na atatumia sehemu ya uzio wa mashamba kama upande wa nne.

Pata fomu kwa eneo lililofungwa na uzio ikiwa pande za uzio perpendicular kwa uzio uliopo zina urefu$L$.
Ni vipimo gani anapaswa kufanya bustani yake ili kuongeza eneo lililofungwa?

Suluhisho

Hebu kutumia mchoro kama vile Kielelezo$\PageIndex{10}$ kurekodi taarifa iliyotolewa. Pia ni muhimu kuanzisha variable muda,$W$, kuwakilisha upana wa bustani na urefu wa sehemu ya uzio sambamba na uzio mashamba.

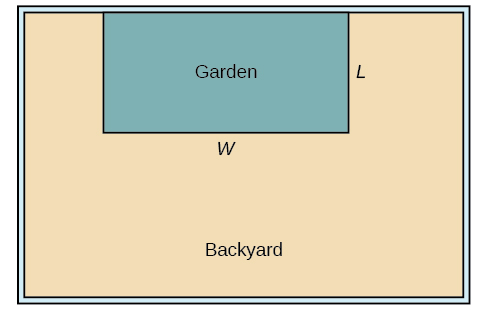
Kielelezo$\PageIndex{10}$: Mchoro wa bustani na mashamba.

Tunajua tuna tu 80 miguu ya uzio inapatikana, na$L+W+L=80$, au zaidi tu,$2L+W=80$. Hii inaruhusu sisi kuwakilisha upana$W$, katika suala la$L$.

\[W=80−2L\]

Sasa tuko tayari kuandika equation kwa eneo ambalo uzio unaingilia. Tunajua eneo la mstatili ni urefu tele kwa upana, hivyo

\[\begin{align} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align}\]

Fomu hii inawakilisha eneo la uzio kulingana na urefu wa kutofautiana$L$. Kazi, iliyoandikwa kwa fomu ya jumla, ni

\[A(L)=−2L^2+80L\].

Quadratic ina mgawo wa kuongoza hasi, hivyo grafu itafungua chini, na vertex itakuwa thamani ya juu kwa eneo hilo. Katika kutafuta kipeo, ni lazima tuwe makini kwa sababu equation haijaandikwa katika fomu ya kawaida ya polynomial na nguvu za kupungua. Hii ni kwa nini sisi rewrote kazi katika fomu ya jumla hapo juu. Tangu$a$ ni mgawo wa muda wa mraba,$a=−2$,$b=80$, na$c=0$.

Ili kupata vertex:

\[\begin{align} h& =−\dfrac{80}{2(−2)} &k&=A(20) \\ &=20 & \text{and} \;\;\;\; &=80(20)−2(20)^2 \\ &&&=800 \end{align}\]

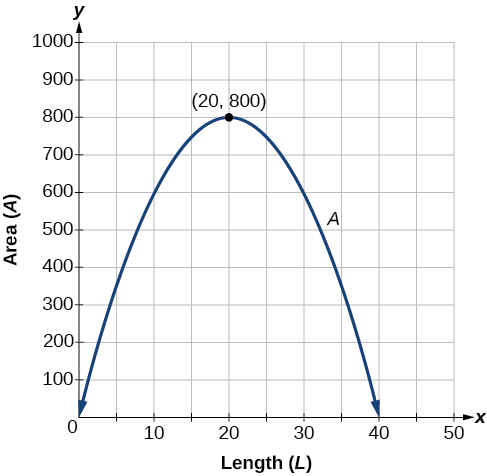
Thamani ya juu ya kazi ni eneo la miguu ya mraba 800, ambayo hutokea wakati$L=20$ miguu. Wakati pande fupi ni miguu 20, kuna miguu 40 ya uzio iliyoachwa kwa upande mrefu. Ili kuongeza eneo hilo, anapaswa kuzunguka bustani ili pande mbili fupi zina urefu wa miguu 20 na upande mrefu unaofanana na uzio uliopo una urefu wa miguu 40.

Uchambuzi

Tatizo hili pia linaweza kutatuliwa kwa kuchora kazi ya quadratic. Tunaweza kuona ambapo eneo la juu hutokea kwenye grafu ya kazi ya quadratic katika Kielelezo$\PageIndex{11}$.

Grafu ya kazi ya parabolic A (L) =-2L ^ 2+80L, ambayo x-axis inaitwa Urefu (L) na y-mhimili ni kinachoitwa Area (A). Vertex iko (20, 800). — Kielelezo$\PageIndex{11}$: Grafu ya kazi ya parabolic$A(L)=-2L^2+80L$

$alt$ Kutokana na programu inayohusisha mapato, tumia equation ya quadratic ili kupata kiwango cha juu.

Andika equation quadratic kwa mapato.
Pata vertex ya equation ya quadratic.
Tambua thamani ya y ya vertex.

Mfano$\PageIndex{6}$: Finding Maximum Revenue

Bei ya kitengo cha kipengee huathiri ugavi na mahitaji yake. Hiyo ni, ikiwa bei ya kitengo inakwenda, mahitaji ya kipengee yatapungua. Kwa mfano, gazeti la ndani kwa sasa lina wanachama 84,000 kwa malipo ya robo mwaka ya $30. Utafiti wa soko umependekeza kwamba kama wamiliki kuongeza bei ya $32, wangeweza kupoteza wanachama 5,000. Kutokana kwamba usajili ni linearly kuhusiana na bei, ni bei gani gazeti lazima malipo kwa ajili ya usajili robo mwaka ili kuongeza mapato yao?

Suluhisho

Mapato ni kiasi cha fedha kampuni huleta. Katika kesi hiyo, mapato yanaweza kupatikana kwa kuzidisha bei kwa kila mara ya usajili idadi ya wanachama, au wingi. Tunaweza kuanzisha vigezo,$p$ kwa bei kwa michango na$Q$ kwa wingi, kutupa equation$\text{Revenue}=pQ$.

Kwa sababu idadi ya wanachama inabadilika na bei, tunahitaji kupata uhusiano kati ya vigezo. Tunajua kwamba kwa sasa$p=30$ na$Q=84,000$. Pia tunajua kwamba kama bei kuongezeka kwa $32, gazeti kupoteza wanachama 5,000, kutoa jozi ya pili ya maadili,$p=32$ na$Q=79,000$. Kutokana na hili tunaweza kupata equation linear zinazohusiana kiasi mbili. Mteremko utakuwa

\[\begin{align} m&=\dfrac{79,000−84,000}{32−30} \\ &=−\dfrac{5,000}{2} \\ &=−2,500 \end{align}\]

Hii inatuambia karatasi kupoteza 2,500 wanachama kwa kila dola wao kuongeza bei. Tunaweza kisha kutatua kwa y-intercept.

\[\begin{align} Q&=−2500p+b &\text{Substitute in the point $Q=84,000$ and $p=30$} \\ 84,000&=−2500(30)+b &\text{Solve for $b$} \\ b&=159,000 \end{align}\]

Hii inatupa equation linear$Q=−2,500p+159,000$ zinazohusiana gharama na wanachama. Sasa tunarudi kwenye equation yetu ya mapato.

\[\begin{align} \text{Revenue}&=pQ \\ \text{Revenue}&=p(−2,500p+159,000) \\ \text{Revenue}&=−2,500p^2+159,000p \end{align}\]

Sasa tuna kazi ya quadratic kwa mapato kama kazi ya malipo ya usajili. Ili kupata bei ambayo itaongeza mapato kwa gazeti, tunaweza kupata vertex.

\[\begin{align} h&=−\dfrac{159,000}{2(−2,500)} \\ &=31.8 \end{align}\]

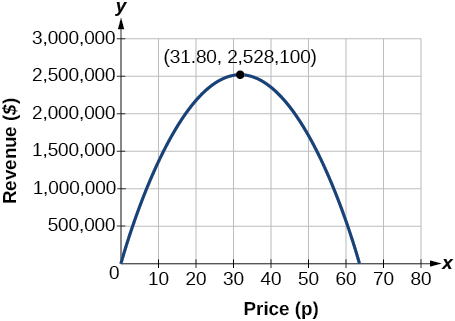
Mfano huo unatuambia kwamba mapato ya juu yatatokea ikiwa gazeti linadai $31.80 kwa usajili. Ili kupata mapato ya juu ni nini, tunatathmini kazi ya mapato.

\[\begin{align} \text{maximum revenue}&=−2,500(31.8)^2+159,000(31.8) \\ &=2,528,100 \end{align}\]

Uchambuzi

Hii inaweza pia kutatuliwa kwa graphing quadratic kama katika Kielelezo$\PageIndex{12}$. Tunaweza kuona mapato ya juu kwenye grafu ya kazi ya quadratic.

Grafu ya kazi parabolic ambayo x-mhimili ni kinachoitwa Bei (p) na y-mhimili ni kinachoitwa Mapato ($). Kipeo ni saa (31.80, 258100). — Kielelezo$\PageIndex{12}$: Grafu ya kazi ya parabolic

Kutafuta x- na Y-intercepts ya Kazi Quadratic

Kama vile tulivyofanya katika matatizo ya maombi hapo juu, tunahitaji pia kupata intercepts ya equations quadratic kwa graphing parabolas. Kumbuka kwamba tunapata y-intercept ya quadratic kwa kutathmini kazi kwa pembejeo ya sifuri, na tunapata x-intercepts katika maeneo ambapo pato ni sifuri. Taarifa katika Kielelezo$\PageIndex{13}$ kwamba idadi ya x-intercepts inaweza kutofautiana kulingana na eneo la grafu.

<div data-mt-source="1" — Kielelezo$\PageIndex{13}$: Idadi ya x-intercepts ya parabola.

Kielelezo$\PageIndex{13}$: Idadi ya x-intercepts ya parabola.

$alt$ Kutokana na kazi ya quadratic$f(x)$, pata y- na x-intercepts.

Tathmini$f(0)$ ili kupata y-intercept.
Kutatua equation quadratic$f(x)=0$ kupata x-intercepts.

Mfano$\PageIndex{7}$: Finding the y- and x-Intercepts of a Parabola

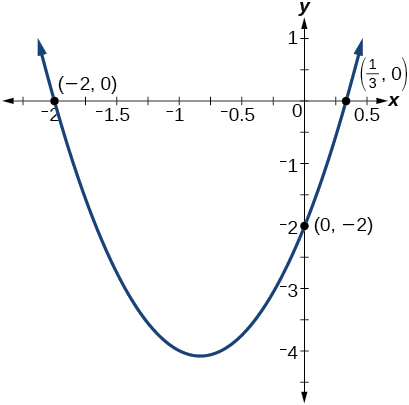
Pata y- na x-intercepts ya quadratic$f(x)=3x^2+5x−2$.

Suluhisho

Tunapata y-intercept kwa kutathmini$f(0)$.

\[\begin{align} f(0)&=3(0)^2+5(0)−2 \\ &=−2 \end{align}\]

Hivyo y-intercept iko$(0,−2)$.

Kwa x-intercepts, tunapata ufumbuzi wote wa$f(x)=0$.

\[0=3x^2+5x−2\]

Katika kesi hiyo, quadratic inaweza kuzingatiwa kwa urahisi, kutoa njia rahisi zaidi ya suluhisho.

\[0=(3x−1)(x+2)\]

\[\begin{align} 0&=3x−1 & 0&=x+2 \\ x&= \frac{1}{3} &\text{or} \;\;\;\;\;\;\;\; x&=−2 \end{align}\]

Hivyo x-intercepts ni saa$(\frac{1}{3},0)$ na$(−2,0)$.

Uchambuzi

Kwa kuchora kazi, tunaweza kuthibitisha kwamba grafu huvuka$y$ mhimili$(0,−2)$. Tunaweza pia kuthibitisha kwamba grafu huvuka x-axis saa$\Big(\frac{1}{3},0\Big)$ na$(−2,0)$. Angalia Kielelezo$\PageIndex{14}$.

Grafu ya parabola ambayo ina intercepts zifuatazo (-2, 0), (1/3, 0), na (0, -2). — Kielelezo$\PageIndex{14}$: Grafu ya parabola.

Kuandika tena Quadratics katika Fomu ya kawaida

Katika Mfano$\PageIndex{7}$, quadratic ilikuwa rahisi kutatuliwa kwa factoring. Hata hivyo, kuna quadratics nyingi ambazo haziwezi kuhesabiwa. Tunaweza kutatua quadratics hizi kwa kwanza kuandika tena kwa fomu ya kawaida.

$alt$ Kutokana na kazi ya quadratic, pata x-intercepts kwa kuandika tena kwa fomu ya kawaida.

Mbadala a na$b$ katika$h=−\frac{b}{2a}$.
$x=h$Kuweka katika fomu ya jumla ya kazi ya quadratic kupata$k$.
Andika upya quadratic katika fomu ya kawaida kwa kutumia$h$ na$k$.
Tatua kwa wakati pato la kazi litakuwa sifuri ili kupata x-intercepts.

Mfano$\PageIndex{8}$: Finding the x-Intercepts of a Parabola

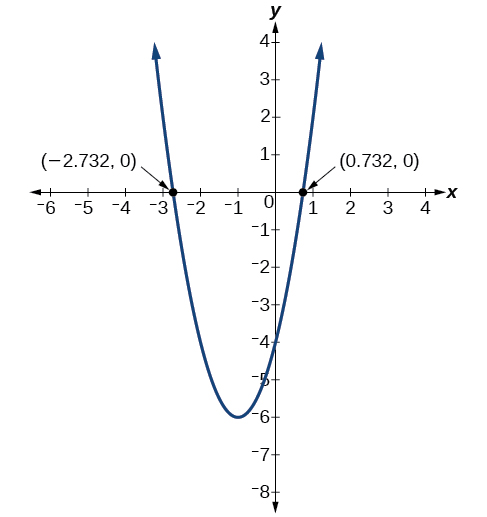
Pata x-intercepts ya kazi ya quadratic$f(x)=2x^2+4x−4$.

Suluhisho

Tunaanza kwa kutatua wakati pato litakuwa sifuri.

\[0=2x^2+4x−4 \nonumber\]

Kwa sababu quadratic haipatikani kwa urahisi katika kesi hii, tunatatua kwa kuingilia kwa mara ya kwanza kuandika tena quadratic katika fomu ya kawaida.

\[f(x)=a(x−h)^2+k\nonumber\]

Tunajua kwamba$a=2$. Kisha sisi kutatua kwa$h$ na$k$.

\[\begin{align*} h&=−\dfrac{b}{2a} & k&=f(−1) \\ &=−\dfrac{4}{2(2)} & &=2(−1)^2+4(−1)−4 \\ &=−1 & &=−6 \end{align*}\]

Hivyo sasa tunaweza kuandika upya katika fomu ya kawaida.

\[f(x)=2(x+1)^2−6\nonumber\]

Sasa tunaweza kutatua kwa wakati pato itakuwa sifuri.

\[\begin{align*} 0&=2(x+1)^2−6 \\ 6&=2(x+1)^2 \\ 3&=(x+1)^2 \\ x+1&={\pm}\sqrt{3} \\ x&=−1{\pm}\sqrt{3} \end{align*}\]

Grafu ina x-intercepts saa$(−1−\sqrt{3},0)$ na$(−1+\sqrt{3},0)$.

Uchambuzi

Tunaweza kuangalia kazi yetu kwa kuchora kazi iliyotolewa kwenye matumizi ya graphing na kuchunguza x-intercepts. Angalia Kielelezo$\PageIndex{15}$.

Grafu ya parabola ambayo ina zifuatazo x-intercepts (-2.732, 0) na (0.732, 0). — Kielelezo$\PageIndex{15}$: Grafu ya parabola ambayo ina zifuatazo x-intercepts:$(-2.732, 0)$ na$(0.732, 0)$.

Zoezi$\PageIndex{1}$

Katika Jaribu$\PageIndex{1}$, tulipata fomu ya kawaida na ya jumla ya kazi$g(x)=13+x^2−6x$. Sasa tafuta y- na x-intercepts (kama ipo).

Jibu: y-intercept katika$(0, 13)$, Hakuna x-intercepts

Mfano$\PageIndex{9}$: Solving a Quadratic Equation with the Quadratic Formula

Kutatua$x^2+x+2=0$.

Suluhisho

Hebu tuanze kwa kuandika formula ya quadratic:$x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}$.

Wakati wa kutumia formula ya quadratic, tunatambua coefficients$a$,$b$ na$c$. Kwa equation$x^2+x+2=0$, tuna$a=1$,$b=1$, na$c=2$. Kubadilisha maadili haya katika formula tuliyo nayo:

\[\begin{align*} x&=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a} \\ &=\dfrac{−1{\pm}\sqrt{1^2−4⋅1⋅(2)}}{2⋅1} \\ &=\dfrac{−1{\pm}\sqrt{1−8}}{2} \\ &=\dfrac{−1{\pm}\sqrt{−7}}{2} \\ &=\dfrac{−1{\pm}i\sqrt{7}}{2} \end{align*}\]

Ufumbuzi wa equation ni$x=\frac{−1+i\sqrt{7}}{2}$ na$x=\frac{−1-i\sqrt{7}}{2}$ au$x=−\frac{1}{2}+\frac{i\sqrt{7}}{2}$ na$x=\frac{-1}{2}−\frac{i\sqrt{7}}{2}$.

Mfano$\PageIndex{10}$: Applying the Vertex and x-Intercepts of a Parabola

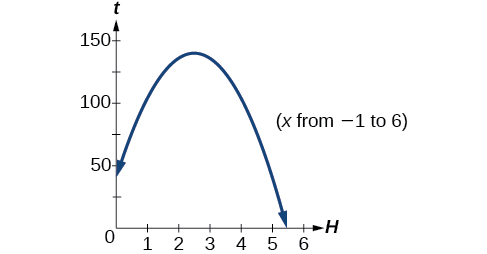
Mpira unatupwa juu kutoka juu ya jengo la urefu wa mguu 40 kwa kasi ya futi 80 kwa sekunde. Urefu wa mpira juu ya ardhi unaweza kuwa inatokana na equation$H(t)=−16t^2+80t+40$.

Mpira unafikia lini urefu wa juu?
Urefu wa juu wa mpira ni nini?
Je! Mpira hupiga wakati gani?

Mpira hufikia urefu wa juu kwenye vertex ya parabola.
\[\begin{align} h &= −\dfrac{80}{2(−16)} \\ &=\dfrac{80}{32} \\ &=\dfrac{5}{2} \\ & =2.5 \end{align}\]

Mpira unafikia urefu wa juu baada ya sekunde 2.5.

Ili kupata urefu wa juu, tafuta y-kuratibu ya vertex ya parabola.
\[\begin{align} k &=H(−\dfrac{b}{2a}) \\ &=H(2.5) \\ &=−16(2.5)^2+80(2.5)+40 \\ &=140 \end{align}\]

Mpira unafikia urefu wa juu wa futi 140.

Ili kupata wakati mpira unapiga ardhi, tunahitaji kuamua wakati urefu ni sifuri,$H(t)=0$.

Tunatumia formula ya quadratic.

\[\begin{align} t & =\dfrac{−80±\sqrt{80^2−4(−16)(40)}}{2(−16)} \\ & = \dfrac{−80±\sqrt{8960}}{−32} \end{align} \]

Kwa sababu mizizi ya mraba haifai vizuri, tunaweza kutumia calculator ili takriban maadili ya ufumbuzi.

\[t=\dfrac{−80-\sqrt{8960}}{−32} ≈5.458 \text{ or }t=\dfrac{−80+\sqrt{8960}}{−32} ≈−0.458 \]

Jibu la pili ni nje ya uwanja wa busara wa mfano wetu, kwa hiyo tunahitimisha mpira utapiga chini baada ya sekunde 5.458. Angalia Kielelezo$\PageIndex{16}$.

$alt$ $\PageIndex{5}$: mwamba ni kutupwa zaidi kutoka juu ya mwamba 112 futi high unaoelekea bahari kwa kasi ya 96 miguu kwa sekunde. Urefu wa mwamba juu ya bahari unaweza kuonyeshwa na equation$H(t)=−16t^2+96t+112$.

Je, mwamba hufikia lini urefu wa juu?
Urefu wa juu wa mwamba ni nini?
Je! Mwamba hupiga bahari lini?

Suluhisho

a. Sekunde 3 b. 256 miguu c. 7 sekunde

Mlinganyo muhimu

fomu ya jumla ya kazi ya quadratic:$f(x)=ax^2+bx+c$
formula ya quadratic:$x=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a}$
fomu ya kawaida ya kazi ya quadratic:$f(x)=a(x−h)^2+k$

Dhana muhimu

Kazi ya polynomial ya shahada mbili inaitwa kazi ya quadratic.
Grafu ya kazi ya quadratic ni parabola. Parabola ni Curve ya U-umbo ambayo inaweza kufungua ama juu au chini.
Mhimili wa ulinganifu ni mstari wa wima unaopitia vertex. Zero, au x-intercepts, ni pointi ambazo parabola huvuka x-axis. Y-intercept ni hatua ambayo parabola huvuka$y$ -axis.
Kazi za Quadratic mara nyingi huandikwa kwa fomu ya jumla. Fomu ya kawaida au vertex ni muhimu kutambua kwa urahisi vertex ya parabola. Fomu yoyote inaweza kuandikwa kutoka kwenye grafu.
Kipeo kinaweza kupatikana kutoka kwa equation inayowakilisha kazi ya quadratic.
Kikoa cha kazi ya quadratic ni namba zote halisi. Aina hiyo inatofautiana na kazi.
Thamani ya chini au ya kiwango cha juu cha kazi ya quadratic inatolewa na thamani ya y ya vertex.
Thamani ya chini au ya juu ya kazi ya quadratic inaweza kutumika kuamua aina mbalimbali za kazi na kutatua aina nyingi za matatizo halisi ya ulimwengu, ikiwa ni pamoja na matatizo yanayohusisha eneo na mapato.
Baadhi ya equations quadratic lazima kutatuliwa kwa kutumia formula quadratic.
Vertex na intercepts inaweza kutambuliwa na kutafsiriwa kutatua matatizo halisi ya ulimwengu.

faharasa

mhimili wa ulinganifu
mstari wima inayotolewa kupitia vertex ya parabola karibu ambayo parabola ni symmetric; inaelezwa na$x=−\frac{b}{2a}$.

jumla fomu ya kazi quadratic kazi
ambayo inaelezea parabola, imeandikwa katika fomu$f(x)=ax^2+bx+c$, ambapo$a,b,$ na$c$ ni idadi halisi na a0.

fomu ya kawaida ya kazi ya quadratic kazi
inayoelezea parabola, iliyoandikwa kwa fomu$f(x)=a(x−h)^2+k$,$(h, k)$ wapi vertex.

vertex
- hatua ambayo parabola inabadilisha mwelekeo, sambamba na thamani ya chini au ya juu ya kazi ya quadratic

aina ya vertex ya kazi ya quadratic (jina
jingine kwa fomu ya kawaida ya kazi ya quadratic)

zeros
katika kazi fulani, maadili ambayo$y=0$, pia hujulikana mizizi$x$

Jedwali\(\PageIndex{1}\)
\(x\)	-6	-4	-2	0	2
\(y\)	-5	-1	-3	-1	5