2.R: Kazi za mstari (Tathmini)

Last updated
Save as PDF

Page ID: 181454

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

2.1 Kazi za mstari

1) Kuamua kama equation algebraic ni linear:$2 x+3 y=7$

Jibu: Ndio

2) Kuamua kama equation algebraic ni linear:$6 x^{2}-y=5$

3) Kuamua kama kazi inaongezeka au kupungua:$f(x)=7 x-2$

Jibu: Kuongezeka

4) Kuamua kama kazi inaongezeka au kupungua:$g(x)=-x+2$

5) Kutokana na kila seti ya habari, pata equation ya mstari ambayo inatimiza hali iliyotolewa, ikiwa inawezekana. Inapita kupitia$(7,5)$ na$(3,17)$

Jibu: $y=-3 x+26$

6) Kutokana na kila seti ya habari, pata equation ya mstari ambayo inatimiza masharti yaliyotolewa, ikiwa inawezekana. $x$-intercept katika$(6,0)$ na$y$ -intercept katika$(0,10)$

7) Pata mteremko wa mstari ulioonyeshwa kwenye grafu ya mstari.

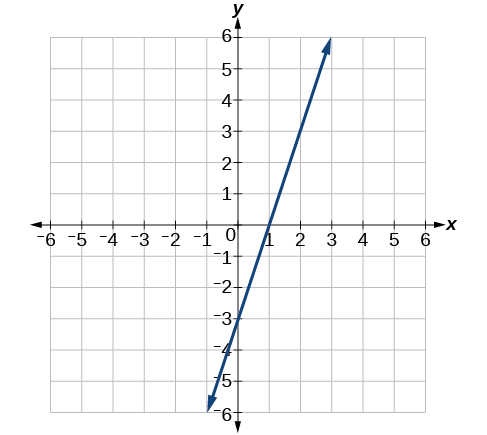
$CNX_Precalc_Figure_02_04_211.jpg$

Jibu: $3$

8) Pata mteremko wa mstari uliowekwa.

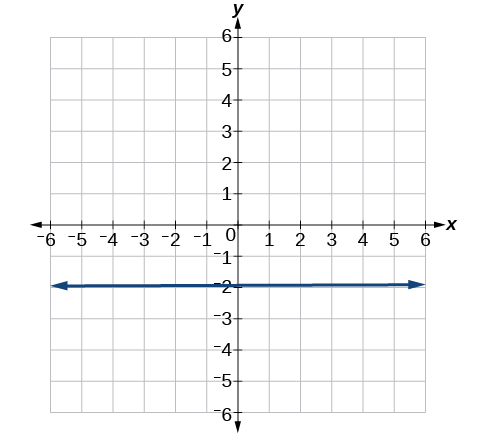
$CNX_Precalc_Figure_02_04_212.jpg$

9) Andika equation katika mteremka-intercept fomu kwa mstari umeonyeshwa.

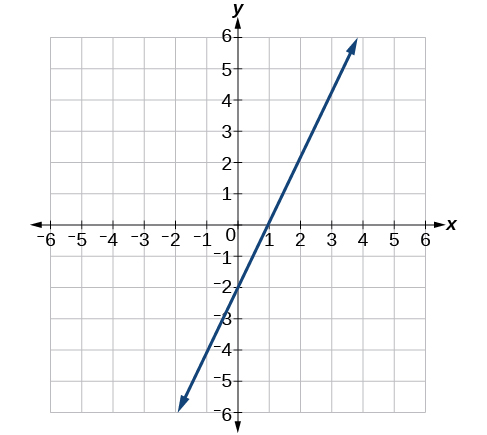
$CNX_Precalc_Figure_02_04_213.jpg$

Jibu: $y=2 x-2$

10) Je, meza ifuatayo inawakilisha kazi ya mstari? Kama ni hivyo, kupata equation linear kwamba mifano data.

$x$	—4	0	2	10
$g(x)$	18	—2	—12	—52

11) Je, meza ifuatayo inawakilisha kazi ya mstari? Kama ni hivyo, kupata equation linear kwamba mifano data.

$x$	6	8	12	26
$g(x)$	—8	—12	—18	—46

Jibu: Si linear

12) Mnamo Juni ¹, kampuni ina$\$4,000,000$ faida. ^{Ikiwa kampuni hiyo inapoteza$150,000$ dola kwa siku baada ya mwezi wa Juni, ni faida gani ya kampuni siku baada ya Juni ¹?}

2.2 Grafu ya Kazi za Mstari

Kwa mazoezi 1-2, onyesha kama mistari iliyotolewa na equations chini ni sambamba, perpendicular, au sambamba wala perpendicular:

1)$\begin{align*} 2x-6y &=12 \\ -x+3y &=1 \end{align*} \nonumber$

Jibu: sambamba

2)$\begin{align*} y &=\dfrac{1}{3} x-2 \\ 3x+y &=-9 \end{align*} \nonumber $

Kwa ajili ya mazoezi 3-4, kupata$x$ - na$y$ - intercepts ya equation kupewa

3)$7 x+9 y=-63$

Jibu: $(-9,0); (0,-7)$

4)$f(x)=2 x-1$

Kwa mazoezi 5-11, tumia maelezo ya jozi ya mistari ili kupata mteremko wa Mstari wa 1 na Mstari wa 2. Je, kila jozi ya mistari sambamba, perpendicular, au wala?

Mstari wa 1: Inapita kupitia$(5,11)$ na$(10,1)$
Line$2 :$ Inapita kupitia$(-1,3)$ na$(-5,11)$

Jibu: Mstari wa 1:$m=-2$; Mstari wa 2:$m=-2$; Sambamba

Mstari wa 1: Inapita kupitia$(8,-10)$ na$(0,-26)$
Line 2: Inapita kupitia$(2,5)$ na$(4,4)$

7) Andika equation kwa mstari perpendicular$f(x)=5 x-1$ na kupitia hatua$(5,20)$.

Jibu: $y=-0.2 x+21$

8) Pata equation ya mstari na$y$ -intercept ya$(0,2)$ na mteremko$-\dfrac{1}{2}$.

9) Mchoro grafu ya kazi ya mstari$f(t)=2t-5$.

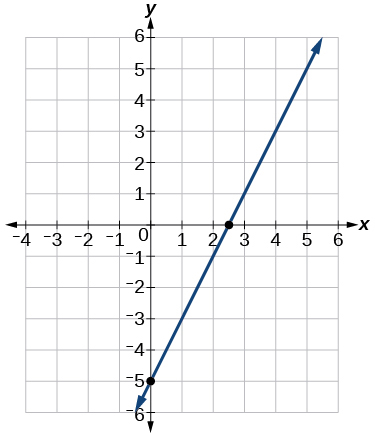
Jibu: $CNX_Precalc_Figure_02_04_214.jpg$

10) Pata hatua ya makutano kwa kazi za$2$ mstari:$\begin{align*} x &=y+6 \\ 2x-y &=13 \end{align*}$

11) Kampuni ya kukodisha gari inatoa mipango miwili ya kukodisha gari.

Mpango A:$25$ dola kwa siku na$10$ senti kwa maili

Mpango B:$50$ dola kwa siku na mileage ya bure isiyo na ukomo

Ni maili ngapi ungehitaji kuendesha gari kwa mpango B ili kukuokoa pesa?

Jibu: $250$

2.3 Mfano na Kazi za Mstari

1) Pata eneo la pembetatu lililofungwa na$y$ mhimili, mstari$f(x)=10-2x$, na mstari unaozingatia$f$ kwamba hupita kupitia asili.

2) idadi ya wakazi wa mji huongezeka kwa kiwango cha mara kwa mara. Mwaka 2010 idadi ya wakazi ilikuwa$55,000$. Kufikia 2012 idadi ya watu iliongezeka hadi$76,000$. Kama hali hii inaendelea, kutabiri idadi ya watu katika 2016.

Jibu: $118,000$

3) Idadi ya watu wanaosumbuliwa na baridi ya kawaida katika miezi ya baridi imeshuka kwa kasi kwa$50$ kila mwaka tangu 2004 hadi 2010. Mwaka 2004,$875$ watu walitolewazwa.

4) Pata kazi ya mstari ambayo inafanana na idadi ya watu wanaosumbuliwa na baridi ya kawaida$C$ kama kazi ya mwaka,$t$. Hakuna mtu atakayeteswa lini?

Kwa mazoezi 5-6, tumia grafu katika Kielelezo hapa chini kuonyesha faida$y$, kwa maelfu ya dola, ya kampuni katika mwaka fulani$x$, ambapo$x$ inawakilisha miaka tangu 1980.

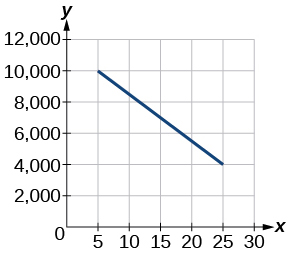
$CNX_Precalc_Figure_02_04_215.jpg$

5) Pata kazi ya mstari$y$, ambapo$y$ inategemea$x$, idadi ya miaka tangu 1980.

Jibu: $y=-300 x+11,500$

6) Tafuta na kutafsiri$y$ -intercept.

7) Kwa zoezi zifuatazo, fikiria hali hii: Mwaka 2004, idadi ya shule ilikuwa$1,700$. By 2012 idadi ya watu walikuwa imeongezeka kwa$2,500$. Tuseme idadi ya watu inabadilika linearly.

Idadi ya watu ilikua kiasi gani kati ya mwaka 2004 na 2012?
Ukuaji wa wastani wa idadi ya watu kwa mwaka ni nini?
Kupata equation kwa idadi ya watu$P$,, ya$t$ miaka ya shule baada ya 2004.

Jibu

$800$
$100$wanafunzi kwa mwaka
$P(t)=100 t+1700$

Kwa mazoezi 8-9, fikiria hali hii: Mwaka 2000, idadi ya watu katika bustani ilipimwa kuwa$6,500$. Kufikia mwaka 2010, idadi ya watu ilipimwa kuwa$12,500$. Kudhani idadi ya watu inaendelea kubadilika linearly.

8) Pata fomu kwa idadi ya watu,$P$.

9) Je! Mfano wako unatabiri nini idadi ya watu kuwa katika 2020?

Jibu: $18,500$

Kwa mazoezi 10-, fikiria hali hii: Maadili ya nyumbani ya wastani katika migawanyiko ya Pima Kati na Mashariki Valley (kubadilishwa kwa mfumuko wa bei) yanaonyeshwa katika Jedwali hapa chini. Fikiria kwamba maadili ya nyumba yanabadilika kwa mstari.

Mwaka	Pima Kati	Bonde la Mashariki
1970	32,000	120,250
2010	85,000	150,000

10) Katika ugawaji gani una maadili ya nyumbani yaliongezeka kwa kiwango cha juu?

11) Ikiwa mwenendo huu utaendelea, ni nini thamani ya wastani ya nyumbani katika Pima Central mwaka 2015?

Jibu: $\$91,625$

2.4 Kufaa Mifano ya Linear kwa Data

1) Chora njama ya kutawanya kwa data katika Jedwali hapa chini. Kisha kuamua kama data inaonekana kuwa linearly kuhusiana.

0	2	4	6	8	10
—105	—50	1	55	105	160

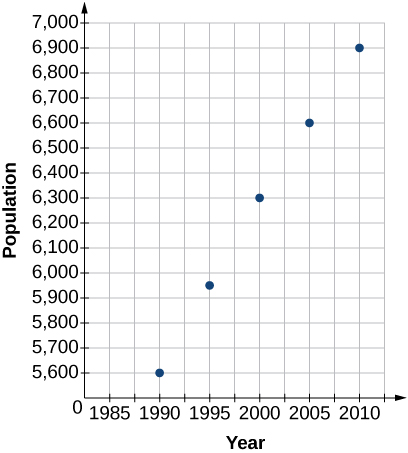
2) Chora njama ya kutawanya kwa data katika Jedwali. Ikiwa tulitaka kujua lini idadi ya watu ingeweza kufikia$15,000$, je, jibu litahusisha ufuatiliaji au extrapolation?

Mwaka	Idadi ya watu
1990	5,600
1995	5,950
2000	6,300
2005	6,600
2010	6,900

Jibu

Extrapolation

$CNX_Precalc_Figure_02_04_226.jpg$

3) Wanafunzi nane waliulizwa kukadiria alama zao kwenye jaribio la$10$ -point. Alama zao za makadirio na halisi zinatolewa katika Jedwali. Panda pointi, kisha mchoro mstari unaofaa data.

Alitabiri	Halisi
6	6
7	7
7	8
8	8
7	9
9	10
10	10
10	9

4) Chora mstari bora zaidi kwa data iliyopangwa.

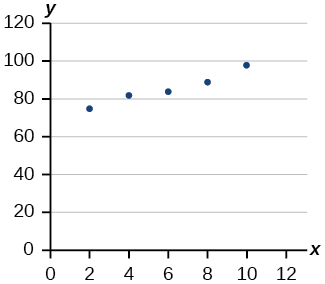
$CNX_Precalc_Figure_02_04_216.jpg$

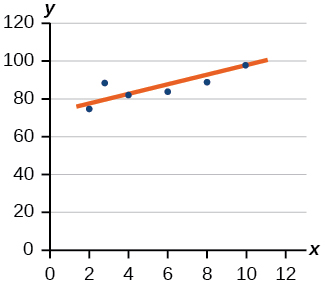
Jibu: $CNX_Precalc_Figure_02_04_217.jpg$

Kwa mazoezi 5-6, fikiria data katika Jedwali hapa chini, ambayo inaonyesha asilimia ya wasio na ajira katika mji wa watu wa$25$ miaka au zaidi ambao ni wahitimu wa chuo kikuu hutolewa hapa chini, kwa mwaka.

Mwaka	Asilimia Wahitimu
2000	6.5
2002	7.0
2005	7.4
2007	8.2
2010	9.0

5) Kuamua kama mwenendo unaonekana kuwa mstari. Kama ni hivyo, na kuchukua mwenendo inaendelea, kupata linear regression mfano kutabiri asilimia ya ajira katika mwaka fulani kwa sehemu tatu decimal.

6) Katika mwaka gani asilimia itazidi$12\%$?

Jibu: Katikati ya 2024

7) Kulingana na seti ya data iliyotolewa katika Jedwali, uhesabu mstari wa kurudi nyuma kwa kutumia calculator au chombo kingine cha teknolojia, na ueleze mgawo wa uwiano kwa maeneo matatu ya decimal.

$x$	17	20	23	26	29
$y$	15	25	31	37	40

8) Kulingana na seti ya data iliyotolewa katika Jedwali, uhesabu mstari wa kurudi nyuma kwa kutumia calculator au chombo kingine cha teknolojia, na ueleze mgawo wa uwiano kwa maeneo matatu ya decimal.

$x$	10	12	15	18	20
$y$	36	34	30	28	22

Jibu: $y=-1.294 x+49.412; r=-0.974$

Kwa mazoezi 9-12, fikiria hali hii: Idadi ya wakazi wa jiji iliongezeka kwa kasi zaidi ya kipindi cha miaka kumi. Jozi zifuatazo zilizoamriwa zinaonyesha idadi ya watu na mwaka juu ya muda wa miaka kumi (idadi ya watu, mwaka) kwa miaka maalum iliyoandikwa:$(3,600,2000) ;(4,000,2001) ;(4,700,2003) ;(6,000,2006)$

9) Tumia regression linear kuamua kazi$y$, ambapo mwaka inategemea idadi ya watu, kwa maeneo matatu decimal ya usahihi.

10) Kutabiri wakati idadi ya watu hit$12,000$.

Jibu: Mapema mwaka 2022

11) Je, ni mgawo wa uwiano wa mfano huu kwa maeneo matatu ya usahihi?

12) Kwa mujibu wa mfano, idadi ya watu ni nini mwaka 2014?

Jibu: $7,660$

Mazoezi mtihani

1) Kuamua kama equation yafuatayo ya algebraic inaweza kuandikwa kama kazi ya mstari:$2 x+3 y=7$

Jibu: Ndio

2) Kuamua kama kazi ifuatayo inaongezeka au kupungua:$f(x)=-2 x+5$

3) Kuamua kama kazi ifuatayo inaongezeka au kupungua:$f(x)=7 x+9$

Jibu: Kuongezeka

4) Kutokana na seti ya habari ifuatayo, pata usawa wa mstari unaoidhinisha hali, ikiwa inawezekana. Inapita kupitia$(5,1)$ na$(3,-9)$

5) Kutokana na seti ya habari ifuatayo, pata usawa wa mstari unaoidhinisha hali, ikiwa inawezekana. $x$kukatiza katika$(-4,0)$ na$y$ -intercept katika$(0,-6)$

Jibu: $y=-1.5 x-6$

6) Pata mteremko wa mstari kwenye Kielelezo hapa chini.

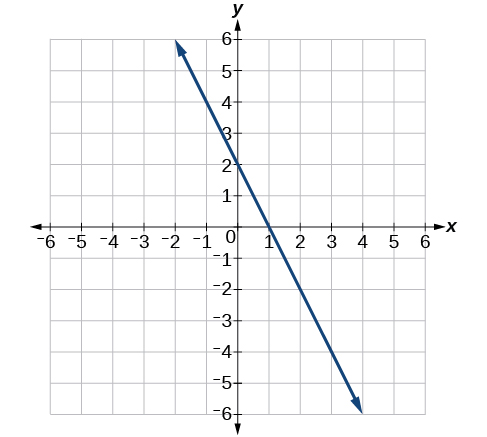
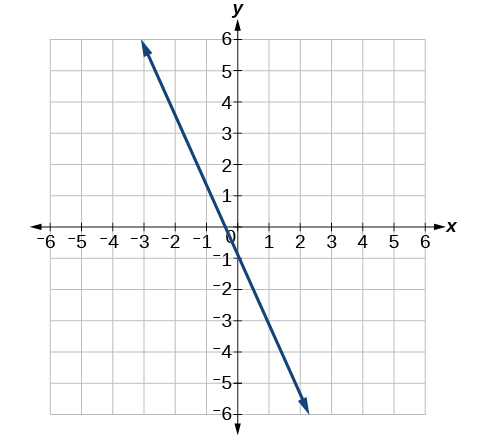
$CNX_Precalc_Figure_02_04_219.jpg$

Jibu: $y=-2 x-1$

8) Je, Jedwali linawakilisha kazi ya mstari? Kama ni hivyo, kupata equation linear kwamba mifano data.

$x$	—6	0	2	4
$g(x)$	14	32	38	44

9) Je, Jedwali linawakilisha kazi ya mstari? Kama ni hivyo, kupata equation linear kwamba mifano data.

$x$	1	3	7	11
$g(x)$	4	9	19	12

Jibu: Hapana

10) Saa 6 asubuhi, kampuni ya mtandaoni imeuza$120$ vitu siku hiyo. Ikiwa kampuni inauza wastani wa$30$ vitu kwa saa kwa salio la siku, andika maneno ili kuwakilisha idadi ya vitu ambavyo viliuzwa$n$ baada ya saa 6 asubuhi.

Kwa mazoezi 11-22, onyesha kama mistari iliyotolewa na equations chini ni sambamba, perpendicular, au sambamba wala perpendicular:

11)$\begin{align*}{y=\dfrac{3}{4} x-9} \\ {-4 x-3 y=8}\end{align*}$

Jibu: Pendicular

12)$\begin{align*}{-2 x+y=3} \\ {3 x+\dfrac{3}{2} y=5}\end{align*}$

13) Kupata$x$ - na$y$ -intercepts ya equation$2 x+7 y=-14$.

Jibu: $(-7,0) ;(0,-2)$

14) Kutokana na hapa chini ni maelezo ya mistari miwili. Pata mteremko wa Mstari wa 1 na Mstari wa 2. Je, jozi ya mistari sambamba, perpendicular, au wala?

Line$1 :$ Inapita kupitia$(-2,-6)$ na$(3,14)$
Line$2 :$ Inapita kupitia$(2,6)$ na$(4,14)$

15) Andika equation kwa mstari perpendicular$f(x)=4 x+3$ na kupitia hatua$(8,10)$.

Jibu: $y=-0.25 x+12$

16) Mchoro mstari na$y$ -intercept ya$(0,5)$ na mteremko$-\dfrac{5}{2}$.

17) Grafu ya kazi ya mstari$f(x)=-x+6$.

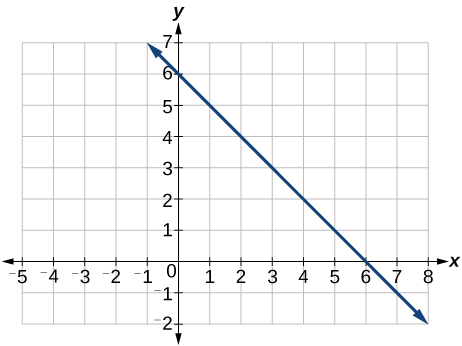
Jibu: $CNX_Precalc_Figure_02_04_221.jpg$

18) Kwa kazi mbili za mstari, pata hatua ya makutano:$\begin{align*} x &=y+2 \\ 2x-3y &=-1 \end{align*}$

19) Kampuni ya kukodisha gari inatoa mipango miwili ya kukodisha gari.

Mpango A:$\$ 25$ kwa$\$ 0.10$ siku na kwa maili
Mpango B:$\$ 40$ kwa siku na mileage ya bure isiyo na ukomo

Ni maili ngapi ungehitaji kuendesha gari kwa mpango B ili kukuokoa pesa?

Jibu: $150$

20) Pata eneo la pembetatu lililofungwa na$y$ mhimili, mstari$f(x)=12-4 x,$ na mstari unaozingatia$f$ kwamba hupita kupitia asili.

21) idadi ya wakazi wa mji huongezeka kwa kiwango cha mara kwa mara. Mwaka 2010 idadi ya wakazi ilikuwa$65,000$. Kufikia 2012 idadi ya watu iliongezeka hadi$90,000$. Kutokana hali hii inaendelea, kutabiri idadi ya watu katika 2018.

Jibu: $165,000$

22) Idadi ya watu waliosumbuliwa na baridi ya kawaida katika miezi ya baridi imeshuka kwa kasi kwa$25$ kila mwaka tangu 2002 hadi 2012. Mwaka 2002,$8,040$ watu walitolewazwa. Kupata kazi linear kwamba mifano ya idadi ya watu wanaosumbuliwa na baridi ya kawaida$C$ kama kazi ya mwaka,$t$. Lini chini ya$6,000$ watu watateswa lini?

Kwa mazoezi 23-24, tumia grafu katika Kielelezo, kuonyesha faida$y$, kwa maelfu ya dola, ya kampuni katika mwaka fulani$x$, ambapo$x$ inawakilisha miaka tangu 1980.

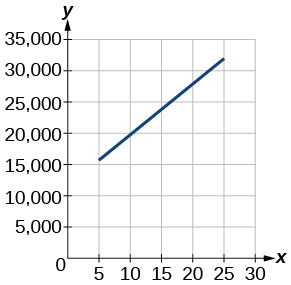
$CNX_Precalc_Figure_02_04_222.jpg$

23) Pata kazi ya mstari$y$, ambapo$y$ inategemea$x$, idadi ya miaka tangu 1980.

Jibu: $y=875 x+10,675$

24) Tafuta na kutafsiri$y$ -intercept.

25) Mwaka 2004, idadi ya shule ilikuwa$1250$. By 2012 idadi ya watu imeshuka kwa$875$. Tuseme idadi ya watu inabadilika linearly.

Idadi ya watu imeshuka kiasi gani kati ya mwaka 2004 na 2012?
Je, wastani wa idadi ya watu kushuka kwa mwaka ni nini?
Kupata equation kwa idadi ya watu$P$,, ya$t$ miaka ya shule baada ya 2004.

Jibu

$375$
imeshuka wastani wa$46.875,$ au juu ya$47$ watu kwa mwaka
$y=-46.875 t+1250$

26) Chora njama ya kutawanya kwa data iliyotolewa katika Jedwali. Kisha kuamua kama data inaonekana kuwa linearly kuhusiana.

0	2	4	6	8	10
—450	—200	10	265	500	755

27) Chora mstari bora zaidi kwa data iliyopangwa.

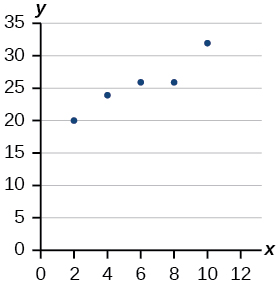
$CNX_Precalc_Figure_02_04_223.jpg$

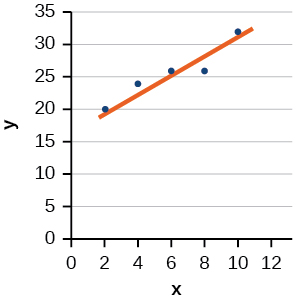
Jibu: $CNX_Precalc_Figure_02_04_224.jpg$

Kwa mazoezi 28-29, tumia Jedwali hapa chini, ambalo linaonyesha asilimia ya watu wasio na ajira$25$ miaka au zaidi ambao ni wahitimu wa chuo kikuu katika mji fulani, kwa mwaka.

Mwaka	Asilimia Wahitimu
2000	8.5
2002	8.0
2005	7.2
2007	6.7
2010	6.4

28) Kuamua kama mwenendo unaonekana linear. Kama ni hivyo, na kuchukua mwenendo inaendelea, kupata linear regression mfano kutabiri asilimia ya ajira katika mwaka fulani kwa sehemu tatu decimal.

29) Katika mwaka gani asilimia itashuka chini$4\%$?

Jibu: Mapema mwaka 2018

30) Kulingana na seti ya data iliyotolewa katika Jedwali hapa chini, uhesabu mstari wa kurudi nyuma kwa kutumia calculator au chombo kingine cha teknolojia, na ueleze mgawo wa uwiano. Pande zote kwa maeneo matatu ya decimal ya usahihi.

$x$	16	18	20	24	26
$y$	106	110	115	120	125

Kwa mazoezi 31-33, fikiria hali hii: Idadi ya wakazi wa jiji iliongezeka kwa kasi zaidi ya kipindi cha miaka kumi. Jozi zifuatazo zilizoamriwa zinaonyesha idadi ya watu (katika mamia) na mwaka juu ya kipindi cha miaka kumi, (idadi ya watu, mwaka) kwa miaka maalum iliyoandikwa:$(4,500,2000) ;(4,700,2001) ;(5,200,2003) ;(5,800,2006)$

31) Tumia regression linear kuamua kazi y, ambapo mwaka inategemea idadi ya watu. Pande zote kwa maeneo matatu ya decimal ya usahihi.

Jibu: $y=0.00455 x+1979.5$

32) Kutabiri wakati idadi ya watu hit$20,000$.

33) Mgawo wa uwiano wa mfano huu ni nini?

Jibu: $r=0.999$

\(x\)	17	20	23	26	29
\(y\)	15	25	31	37	40

\(x\)	10	12	15	18	20
\(y\)	36	34	30	28	22

\(x\)	—6	0	2	4
\(g(x)\)	14	32	38	44

\(x\)	1	3	7	11
\(g(x)\)	4	9	19	12