2.E: Kazi za mstari (Mazoezi)

Last updated
Save as PDF

Page ID: 181406

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

2.1 Kazi za mstari

Maneno

1) Terry ni skiing chini ya kilima mwinuko. Mwinuko wa Terry$E(t)$,, kwa miguu baada ya$t$ sekunde hutolewa na$E(t)=3000−70t$. Andika sentensi kamili inayoelezea mwinuko wa mwanzo wa Terry na jinsi unavyobadilika baada ya muda.

Jibu: Terry huanza kwenye mwinuko wa$3000$ miguu na kushuka$70$ miguu kwa sekunde.

2) Maria anapanda mlima. Mwinuko Maria$E(t)$,, kwa miguu baada ya$t$ dakika hutolewa na$E(t)=1200+40t$. Andika sentensi kamili inayoelezea mwinuko wa mwanzo wa Maria na jinsi unavyobadilika baada ya muda.

3) Jessica anatembea nyumbani kutoka nyumba ya rafiki. Baada ya$2$ dakika yeye ni$1.4$ maili kutoka nyumbani. Dakika kumi na mbili baada ya kuondoka, yeye ni$0.9$ maili kutoka nyumbani. Je! Ni kiwango gani cha maili kwa saa?

Jibu: $3$maili kwa saa

4) Sonya sasa ni$10$ maili kutoka nyumbani na anatembea mbali zaidi kwa$2$ maili kwa saa. Andika equation kwa umbali wake kutoka$t$ masaa ya nyumbani tangu sasa.

5) mashua ni$100$ maili mbali na marina, meli moja kwa moja kuelekea kwa$10$ maili kwa saa. Andika equation kwa umbali wa mashua kutoka marina baada ya$t$ masaa.

Jibu: $d(t) =100−10t$

6) Timmy inakwenda haki na$\$40$. Kila gharama za safari$\$2$. Je! Fedha ngapi ataondoka baada ya kuendesha$n$ safari?

Kialjebra

Kwa mazoezi 7-14, onyesha kama equation ya curve inaweza kuandikwa kama kazi linear.

7)$y= \dfrac{1}{4}x+6$

Jibu: Ndio

8)$y=3x−5$

9)$y=3 x^2 −2$

Jibu: Hapana

10)$3x+5y=15$

11)$3 x^2 +5y=15$

Jibu: Hapana

12)$3x+5 y^ 2 =15$

13)$−2 x^2 +3y^2 =6$

Jibu: Hapana

14)$−\dfrac{x−3}{5} =2y$

Kwa mazoezi 15-24, onyesha kama kila kazi inaongezeka au inapungua.

15)$f(x)=4x+3$

Jibu: Kuongezeka

16)$g(x)=5x+6$

17)$a(x)=5−2x$

Jibu: Kupungua

18)$b(x)=8−3x$

19)$h(x)=−2x+4$

Jibu: Kupungua

20)$k(x)=−4x+1$

21)$j(x)=\dfrac{1}{2}x−3$

Jibu: Kuongezeka

22)$p(x)=\dfrac{1}{4}x−5$

23)$n(x)=−\dfrac{1}{3}x−2$

Jibu: Kupungua

24)$m(x)=−\dfrac{3}{8}x+3$

Kwa mazoezi 25-29, tafuta mteremko wa mstari unaopita kupitia pointi mbili zilizopewa.

25)$(2, 4)$ na$(4, 10)$

Jibu: $3$

26)$(1, 5)$ na$(4, 11)$

27)$(−1,4)$ na$(5,2)$

Jibu: $–\dfrac{1}{3}$

28)$(8,−2)$ na$(4,6)$

29) (6, 11) na (-4, 3)

Jibu: $\dfrac{4}{5}$

Kwa mazoezi 30-37, kutokana na kila seti ya habari, kupata equation linear kuridhisha hali, ikiwa inawezekana.

30)$f(−5)=−4$, na$f(5)=2$

31)$f(−1)=4$ na$f(5)=1$

Jibu: $f(x)=−\dfrac{1}{2}x+\dfrac{7}{2}$

32)$(2,4)$ na$(4,10)$

33) Inapita kupitia$(1,5)$ na$(4,11)$

Jibu: $y=2x+3$

34) Inapita kupitia$(−1, 4)$ na$(5, 2)$

35) Inapita kupitia$(−2, 8)$ na$(4, 6)$

Jibu: $y=−\dfrac{1}{3}x+\dfrac{22}{3}$

36)$x$ kukatiza katika (ї2, 0) na$y$ kukatiza katika (0, 1-3)

37)$x$ kukatiza katika (-5, 0) na$y$ kukatiza katika (0, 4)

Jibu: $y=\dfrac{4}{5}x+4$

Picha

Kwa mazoezi 38-,40 kupata mteremko wa mistari iliyowekwa.

38)

$alt$

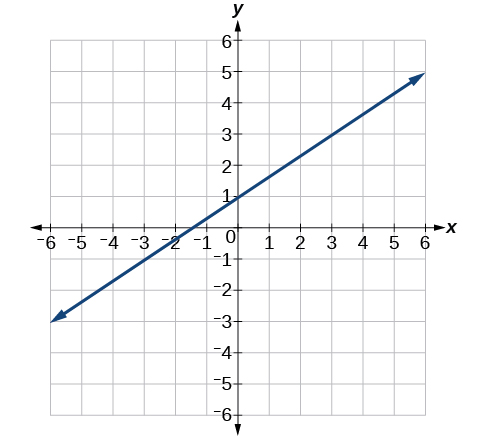
39)

$alt$

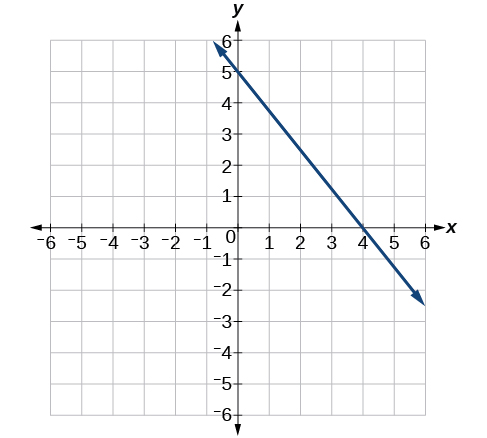
Jibu: $−\dfrac{5}{4}$

40)

$alt$

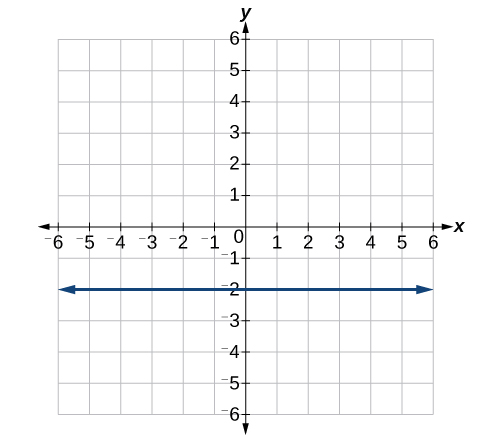
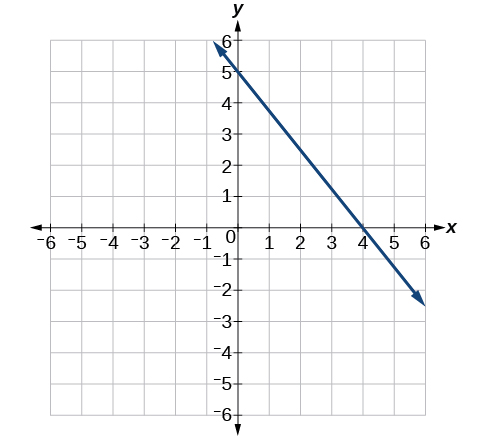
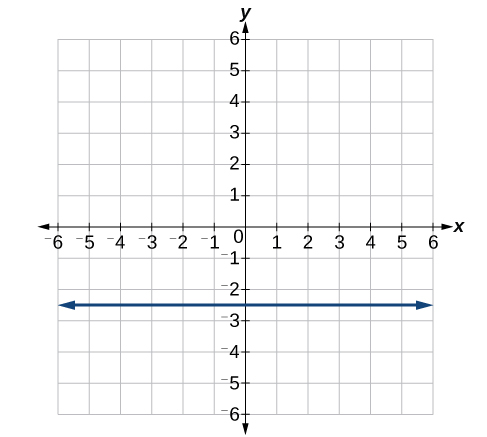
Kwa mazoezi 41-46, andika equation kwa mistari iliyowekwa.

41)

$alt$

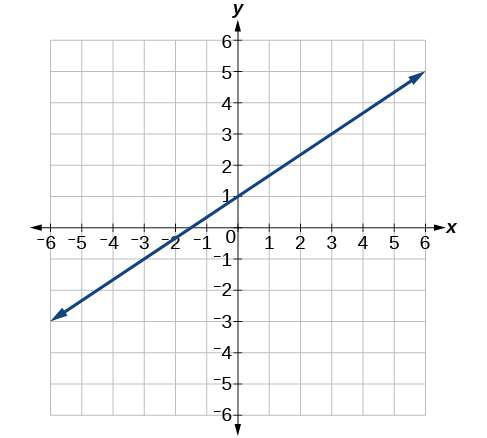
Jibu: $y= \dfrac{2}{3} x+1$

42)

$alt$

43)

$alt$

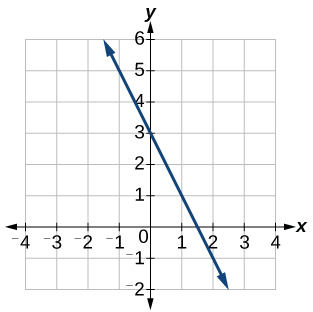
Jibu: $y=−2x+3$

44)

$alt$

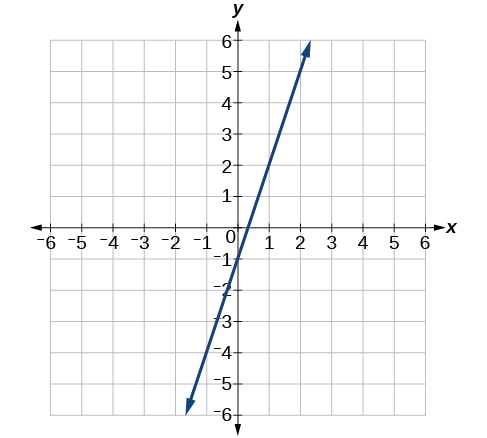
45)

$alt$

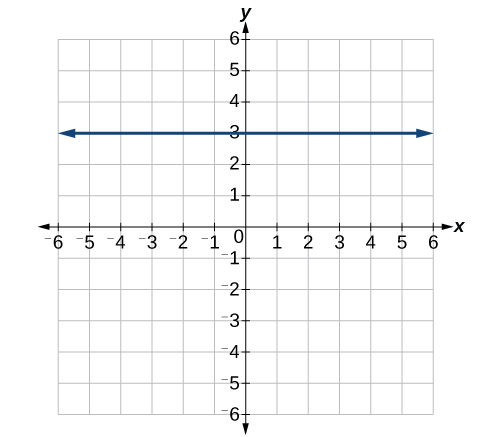
Jibu: $y=3$

46)

$alt$

Numeric

Kwa mazoezi 47-51, ambayo ya meza inaweza kuwakilisha kazi ya mstari? Kwa kila ambayo inaweza kuwa linear, kupata equation linear kwamba mifano data.

47)

$x$	0	5	10	15
$g(x)$	5	—10	—25	—40

Jibu: Mstari,$g(x)=−3x+5$

48)

$x$	0	5	10	15
$h(x)$	5	30	105	230

$x$	0	5	10	15
$f(x)$	—5	20	45	70

Jibu: Mstari,$f(x)=5x−5$

49)

$x$	5	10	20	25
$k(x)$	28	13	58	73

$x$	0	2	4	6
$g(x)$	6	—19	—44	—69

Jibu: Mstari,$g(x)=−\dfrac{25}{2}x+6$

50)

$x$	2	4	6	8
$f(x)$	—4	16	36	56

$x$	2	4	6	8
$f(x)$	—4	16	36	56

Jibu: Mstari,$f(x)=10x−24$

51)

$x$	0	2	6	8
$k(x)$	6	31	106	231

Teknolojia

52) Kama$f$ ni kazi linear,$f(0.1)=11.5$, na$f(0.4)=–5.9$, kupata equation kwa ajili ya kazi.

Jibu: $f(x)=−58x+17.3$

53) Graph kazi$f$ kwenye uwanja wa$[ –10, 10 ]: f(x)=0.02x−0.01$. Ingiza kazi katika matumizi ya graphing. Kwa dirisha la kutazama, weka thamani ya$x$ chini ya kuwa -10 na thamani ya juu$x$ ya kuwa 10.

54) Graph kazi$f$ kwenye uwanja wa$[ –10, 10 ]:fx)=2,500x+4,000$

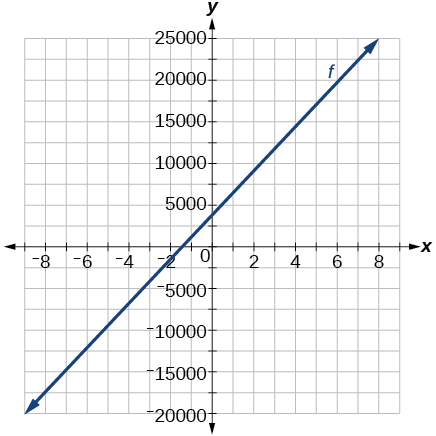
Jibu: $CNX_Precalc_Figure_02_01_214.jpg$

55) Jedwali hapa chini linaonyesha pembejeo$w$,, na pato$k$, kwa kazi ya mstari$k$.

Jaza maadili yasiyopotea ya meza.
Andika kazi ya mstari$k$, pande zote hadi maeneo ya$3$ decimal.

$w$	—10	5.5	67.5	b
$k$	30	—26	a	—44

56) Jedwali hapa chini linaonyesha pembejeo$p$,, na pato$q$, kwa kazi ya mstari$q$.

Jaza maadili yasiyopotea ya meza.
Andika kazi ya mstari$k$.

$p$	0.5	0.8	12	b
$q$	400	700	a	1,000,000

Jibu

$a=11$,900;$b=1001.1$
$q(p)=1000p−100$

57) Graph kazi linear$f$ kwenye uwanja wa$[ −10,10 ]$ kwa ajili ya kazi ambayo mteremko ni$\dfrac{1}{8}$ na y-intercept ni$\dfrac{31}{16}$. Weka alama kwa maadili ya pembejeo ya$−10$ na$10$.

58) Graph kazi linear$f$ kwenye uwanja wa$[ −0.1,0.1 ]$ kwa ajili ya kazi ambayo mteremko ni$75$ na$y$ -intercept ni$-22.5$. Weka alama kwa maadili ya pembejeo ya$-0.1$ na$0.1$.

Jibu: $alt$

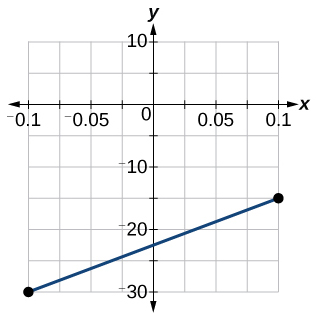
59) Graph kazi linear$f$ ambapo$f(x)=ax+b$ juu ya seti moja ya axes kwenye uwanja wa$[ −4,4 ]$ kwa maadili yafuatayo ya$a$ na$b$.

$a=2;$$b=3$
$a=2; $$b=4$
$a=2;$$b=–4$
$a=2;$$b=–5$

Upanuzi

60) Pata thamani ya$x$ ikiwa kazi ya mstari inapitia pointi zifuatazo na ina mteremko wafuatayo:$(x,2),(−4,6),$$m=3$

Jibu: $x=−\dfrac{16}{3}$

61) Pata thamani ya$y$ ikiwa kazi ya mstari inapitia pointi zifuatazo na ina mteremko wafuatayo:$(10,y),(25,100),$$m=−5$

62) Pata usawa wa mstari unaopita kupitia pointi zifuatazo:$(a, b)$ na$( a, b+1 )$

Jibu: $x=a$

63) Pata usawa wa mstari unaopita kupitia pointi zifuatazo:$(2a, b)$ na (a, b+1)

64) Pata usawa wa mstari unaopita kupitia pointi zifuatazo:$(a, 0)$ na$(c, d)$

Jibu: $y=\dfrac{d}{c−a}x−\dfrac{ad}{c−a}$

Real-World Matumizi

65) saa sita mchana, barista matangazo kwamba ana$\$20$ katika ncha jar yake. Kama yeye hufanya wastani wa$\$0.50$ kutoka kwa kila mteja, ni kiasi gani atakuwa na katika jar yake ncha kama yeye mtumishi wateja$n$ zaidi wakati wa mabadiliko yake?

66) Uanachama mazoezi na mbili binafsi vikao vya mafunzo gharama$\$125$, wakati mazoezi uanachama na vikao tano binafsi mafunzo gharama$\$260$. Ni gharama gani kwa kila kikao?

Jibu: $\$45$kwa kikao cha mafunzo.

67) Biashara ya nguo hupata uhusiano wa mstari kati ya idadi ya mashati$n$, inaweza kuuza na bei$p$, inaweza malipo kwa shati. Hasa, data ya kihistoria inaonyesha kwamba$1,000$ mashati inaweza kuuzwa kwa bei ya$\$30$, wakati$3,000$ mashati inaweza kuuzwa kwa bei ya$\$22$. Kupata equation linear katika fomu$p(n)=mn+b$ ambayo inatoa bei$p$ wanaweza malipo kwa ajili ya$n$ mashati.

68) Kampuni ya simu$n$ inadai huduma kulingana na formula:$C(n)=24+0$ .1n, wapi idadi ya dakika iliyoongea, na$C(n)$ ni malipo ya kila mwezi, kwa dola. Pata na kutafsiri kiwango cha mabadiliko na thamani ya awali.

Jibu: Kiwango cha mabadiliko ni$0.1$. Kwa kila dakika ya ziada kuongea, malipo ya kila mwezi huongezeka kwa$10$ senti$\$0.1$ au. Thamani ya awali ni$24$. Wakati hakuna dakika kuongea, awali malipo ni$\$24$.

69) Mkulima anaona kuna uhusiano wa mstari kati ya idadi ya mabua ya maharagwe$n$, yeye hupanda na mavuno,$y$, kila mmea huzalisha. Wakati yeye hupanda$30$ mabua, kila mmea huzaa$30$ oz ya maharagwe. Wakati yeye hupanda$34$ mabua, kila mmea hutoa$28$ oz ya maharagwe. Pata mahusiano ya mstari katika fomu$y=mn+b$ ambayo inatoa mavuno wakati$n$ mabua yanapandwa.

70) idadi ya wakazi wa mji katika mwaka 1960 ilikuwa$287,500$. Mwaka 1989 idadi ya wakazi ilikuwa$275,900$. Futa kiwango cha ukuaji wa idadi ya watu na kutoa taarifa kuhusu kiwango cha idadi ya watu ya mabadiliko kwa watu kwa mwaka.

Jibu: Mteremko ni$-400$. Hii inamaanisha kwa kila mwaka kati ya 1960 na 1989, idadi ya watu imeshuka$400$ kwa mwaka mjiani.

71) Idadi ya wakazi wa mji imekuwa ikiongezeka kwa mstari. Mwaka 2003, idadi ya watu ilikuwa$45,000$, na idadi ya watu imekuwa ikiongezeka kwa$1,700$ watu kila mwaka. Andika equation,$P(t)$, kwa$t$ miaka ya idadi ya watu baada ya 2003.

72) Tuseme kwamba wastani wa mapato ya kila mwaka (kwa dola) kwa miaka 1990 hadi 1999 hutolewa na kazi ya mstari:$I(x)=1054x+23$,$286,$ wapi$x$ idadi ya miaka baada ya 1990. Ni ipi kati ya yafuatayo inayofafanua mteremko katika mazingira ya tatizo?

Kufikia 1990, wastani wa mapato ya kila mwaka ulikuwa$\$23,286$.
Katika kipindi cha miaka kumi kuanzia 1990-1999, wastani wa mapato ya kila mwaka uliongezeka kwa jumla ya$\$1,054$.
Kila mwaka katika muongo wa miaka ya 1990, wastani wa mapato ya kila mwaka uliongezeka kwa $1,054.
Wastani wa mapato ya kila mwaka uliongezeka hadi kiwango cha dola 23,286 mwishoni mwa 1999.

Jibu: c

73) Wakati joto ni$0$ digrii Celsius, joto la Fahrenheit ni$32$. Wakati joto la Celsius ni$100$, joto la Fahrenheit linalofanana ni$212$. Express joto Fahrenheit kama kazi linear ya$C$, joto Celsius,$F(C)$.

Kupata kiwango cha mabadiliko ya joto Fahrenheit kwa kila kitengo mabadiliko ya joto ya Celsius.
Pata na kutafsiri$F(28)$.
Pata na kutafsiri$F(–40)$.

2.2 Grafu ya Kazi za Mstari

Maneno

1) Ikiwa grafu ya kazi mbili za mstari ni sawa, kuelezea uhusiano kati ya mteremko na$y$ -intercepts.

Jibu: Miteremko ni sawa;$y$ -intercepts si sawa.

2) Ikiwa grafu ya kazi mbili za mstari ni perpendicular, kuelezea uhusiano kati ya mteremko na$y$ -intercepts.

3) Ikiwa mstari wa usawa una equation$f(x)=a$ na mstari wa wima una equation$x=a$, ni hatua gani ya makutano? Eleza kwa nini ulichopata ni hatua ya makutano.

Jibu: Hatua ya makutano ni$(a,a)$. Hii ni kwa sababu kwa mstari usawa, wote wa$y$ kuratibu ni na kwa mstari wima, wote wa$x$ kuratibu ni. hatua ya makutano itakuwa na sifa hizi mbili.

4) Eleza jinsi ya kupata mstari sambamba na kazi linear ambayo hupita kupitia hatua fulani.

5) Eleza jinsi ya kupata mstari perpendicular kwa kazi linear ambayo hupita kupitia hatua fulani.

Jibu: Kwanza, tafuta mteremko wa kazi ya mstari. Kisha kuchukua usawa mbaya wa mteremko; hii ni mteremko wa mstari wa perpendicular. Kuweka mteremko wa mstari wa perpendicular na kuratibu ya hatua iliyotolewa katika equation$y=mx+b$ na kutatua$b$. Kisha kuandika equation ya mstari katika fomu$y=mx+b$ kwa kubadili$m$ na$b$.

Kialjebra

Kwa mazoezi 6-11, onyesha kama mistari iliyotolewa na equations chini ni sambamba, perpendicular, au sambamba wala perpendicular:

6)$4x−7y=10 \\ 7x+4y=1$

7)$3y+x=12 \\ −y=8x+1$

Jibu: wala sambamba au kwa pembeni

8)$3y+4x=12 \\ −6y=8x+1$

9)$6x−9y=10 \\ 3x+2y=1$

Jibu: wima

10)$y=\dfrac{2}{3}x+1 \\ 3x+2y=1$

11)$y=\dfrac{3}{4}x+1 \\ −3x+4y=1$

Jibu: sambamba

Kwa ajili ya mazoezi 12-17, kupata$x$ - na$y$ -intercepts ya kila equation

12)$f(x)=−x+2$

13)$g(x)=2x+4$

Jibu: $(–2, 0); (0, 4)$

14)$h(x)=3x−5$

15)$k(x)=−5x+1$

Jibu: $\left(\dfrac{1}{5}, 0\right); (0, 1)$

16)$−2x+5y=20$

17)$7x+2y=56$

Jibu: $(8, 0); (0, 28)$

Kwa mazoezi 18-23, tumia maelezo ya kila jozi ya mistari iliyotolewa hapa chini ili kupata mteremko wa Line 1 na Line 2. Je, kila jozi ya mistari sambamba, perpendicular, au wala?

18)

Mstari wa 1: Inapita kupitia$(0,6)$ na$(3,−24)$
Line 2: Inapita kupitia$(−1,19)$ na$(8,−71)$

19)

Mstari wa 1: Inapita kupitia$(−8,−55)$ na$(10, 89)$
Line 2: Inapita kupitia$(9,−44)$ na$(4,−14)$

Jibu: Mstari wa 1:$m=8$ Mstari wa 2:$m=–6$ Wala

20)

Mstari wa 1: Inapita kupitia$(2,3)$ na (4, -1)
Mstari wa 2: Inapita kupitia$(6,3)$ na$(8,5)$

21)

Mstari wa 1: Inapita kupitia$(1,7)$ na$(5,5)$
Line 2: Inapita kupitia$(−1,−3)$ na$(1,1)$

Jibu: Mstari wa 1:$m=–12$ Line 2:$m=2$ Perpendic

22)

Mstari wa 1: Inapita kupitia$(0,5)$ na$(3,3)$
Line 2: Inapita kupitia$(1,−5)$ na$(3,−2)$

23)

Mstari wa 1: Inapita kupitia$(2,5)$ na$(5,−1)$
Line 2: Inapita kupitia$(−3,7)$ na$(3,−5)$

Jibu: Mstari wa 1:$m=–2$ Line 2:$m=–2$ Sambamba

24) Andika equation kwa mstari sambamba$f(x)=−5x−3$ na na kupitia hatua$(2, –12)$.

25) Andika equation kwa mstari sambamba$g(x)=3x−1$ na na kupitia hatua$(4,9)$.

Jibu: $g(x)=3x−3$

26) Andika equation kwa mstari perpendicular$h(t)=−2t+4$ na kupitia hatua$(-4, –1)$.

27) Andika equation kwa mstari perpendicular$p(t)=3t+4$ na kupitia hatua$(3,1)$.

Jibu: $p(t)=−\dfrac{1}{3}t+2$

28) Pata hatua ambayo mstari$f(x)=−2x−1$ unaingilia mstari$g(x)=−x$.

29) Pata hatua ambayo mstari$f(x)=2x+5$ unaingilia mstari$g(x)=−3x−5$.

Jibu: $(−2,1)$

30) Tumia algebra ili kupata hatua ambayo mstari$f(x)= −\dfrac{4}{5}x +\dfrac{274}{25}$ unaingilia mstari$h(x)=\dfrac{9}{4}x + \dfrac{73}{10}$.

31) Tumia algebra ili kupata hatua ambayo mstari$f(x)=\dfrac{7}{4}x + \dfrac{457}{60}$ unaingilia mstari$g(x)=\dfrac{4}{3}x + \dfrac{31}{5}$.

Jibu: $\left(−\dfrac{17}{5},\dfrac{5}{3}\right)$

Picha

Kwa mazoezi 32-37, mechi ya usawa wa mstari uliopewa na grafu yake katika Kielelezo hapa chini.

$alt$

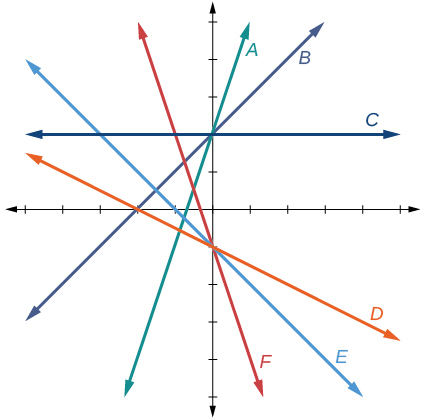
32)$f(x)=−x−1$

33)$f(x)=−2x−1$

Jibu: F

34)$f(x)=−\dfrac{1}{2}x−1$

35)$f(x)=2$

Jibu: C

36)$f(x)=2+x$

37)$f(x)=3x+2$

Jibu: A

Kwa mazoezi 38-43, mchoro mstari na vipengele vilivyopewa.

38)$x$ -intercept ya$(–4, 0)$ na$y$ -intercept ya$(0, –2)$

39)$x$ -intercept ya$(–2, 0)$ na$y$ -intercept ya$(0, 4)$

Jibu: $alt$

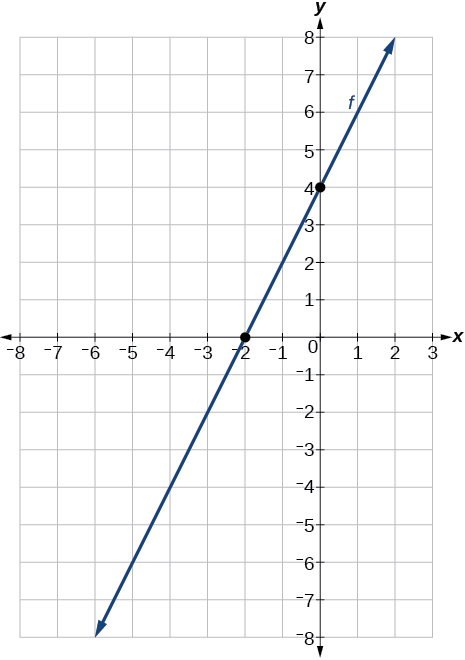
40) A$y$ -intercept ya$(0, 7)$ na mteremko$−\dfrac{3}{2}$

41) A$y$ -intercept ya$(0, 3)$ na mteremko$\dfrac{2}{5}$

Jibu: $alt$

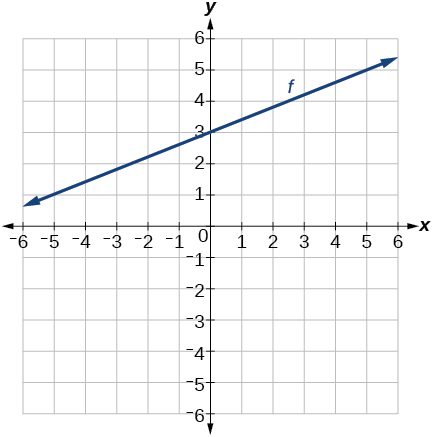
42) Kupitia pointi$(–6, –2)$ na$(6, –6)$

43) Kupitia pointi$(–3, –4)$ na$(3, 0)$

Jibu: $alt$

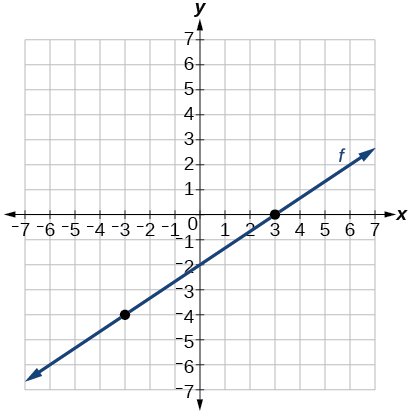
Kwa mazoezi 44-58, mchoro grafu ya kila equation.

44)$f(x)=−2x−1$

45)$g(x)=−3x+2$

Jibu: $alt$

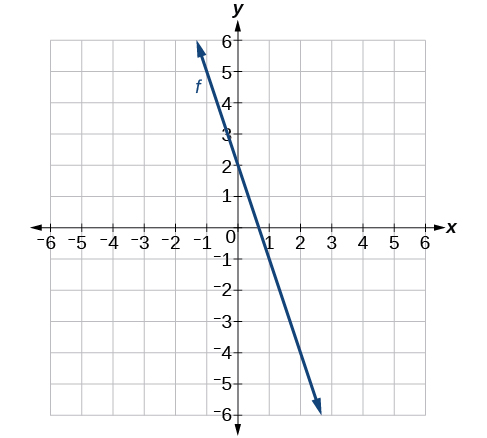
46)$h(x)=\dfrac{1}{3}x+2$

47)$k(x)=\dfrac{2}{3}x−3$

Jibu: $alt$

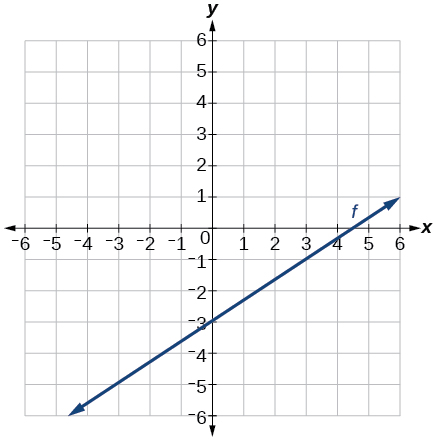
48)$f(t)=3+2t$

49)$p(t)=−2 + 3t$

Jibu: $alt$

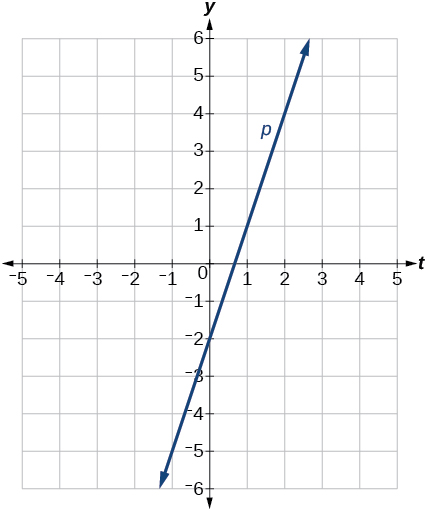
50)$x=3$

51)$x=−2$

Jibu: $alt$

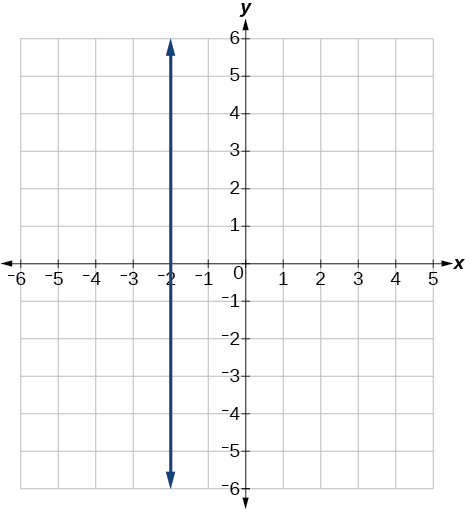
52)$r(x)=4$

53)$q(x)=3$

Jibu: $alt$

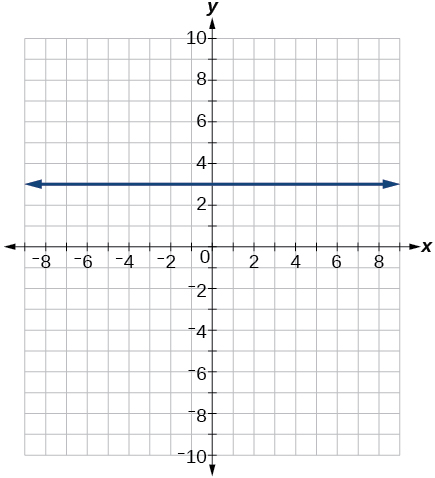
54)$4x=−9y+36$

55)$\dfrac{x}{3}−\dfrac{y}{4}=1$

Jibu: $alt$

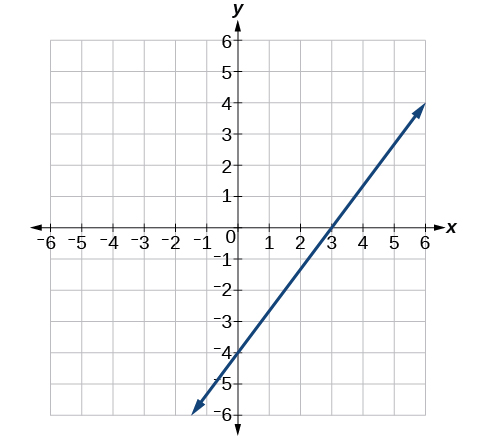
56)$3x−5y=15$

57)$3x=15$

Jibu: $alt$

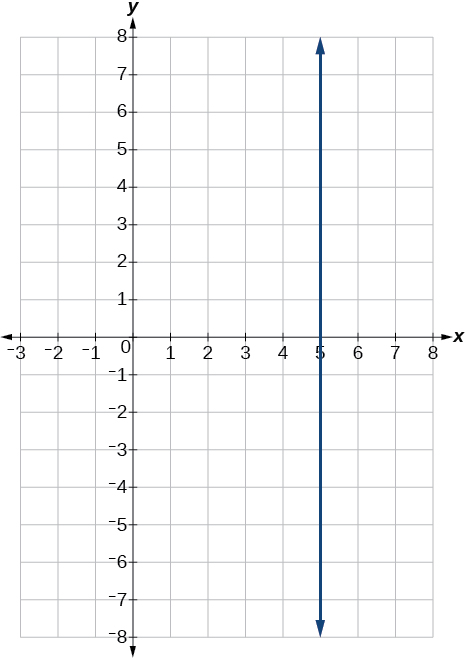
58)$3y=12$

59) Kama$g(x)$ ni mabadiliko ya$f(x)=x$ baada compression wima na$\dfrac{3}{4}$, kuhama haki na$2$, na kuhama chini kwa$4$

Andika equation kwa$g(x)$.
Je, ni mteremko wa mstari huu?
Pata$y$ -intercept ya mstari huu.

Jibu

$g(x)=0.75x−5.5$
$0.75$
$0,-5.5)$

60) Kama$g(x)$ ni mabadiliko ya$f(x)=x$ baada compression wima na$\dfrac{1}{3}$, kuhama kushoto na$1$, na kuhama kwa$3$

Andika equation kwa$g(x)$.
Je, ni mteremko wa mstari huu?
Pata$y$ -intercept ya mstari huu.

Kwa mazoezi 61-64, weka usawa wa mstari ulioonyeshwa kwenye grafu.

61)

$alt$

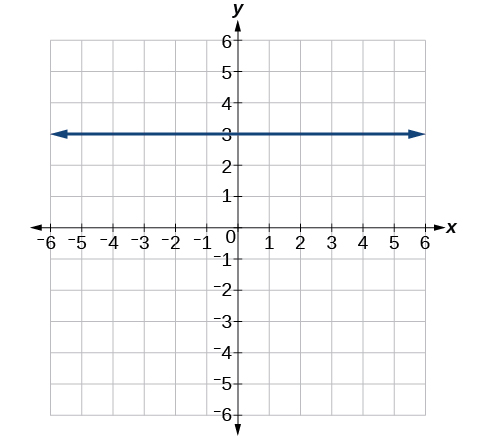
Jibu: $y=3$

62)

$alt$

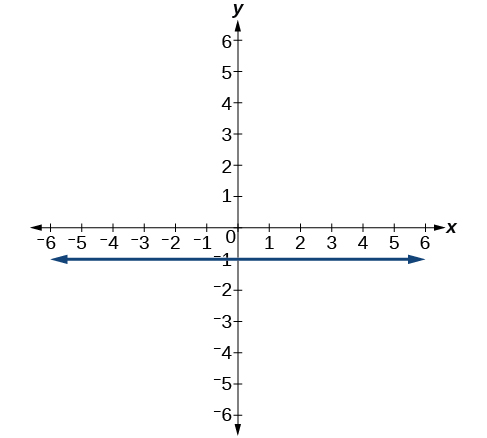
63)

$alt$

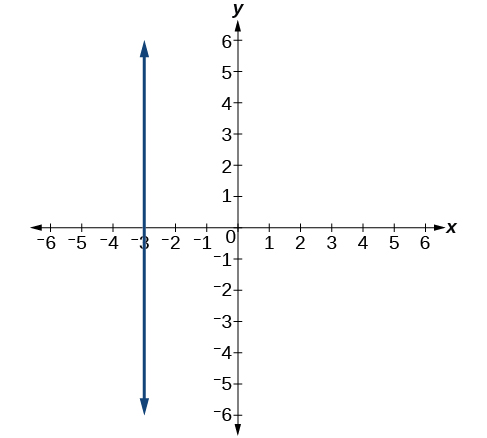
Jibu: $x=−3$

64)

$alt$

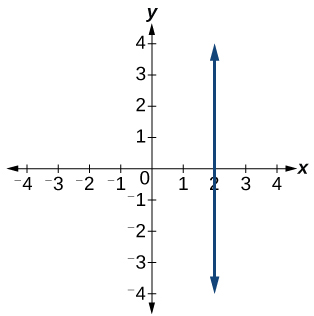
Kwa mazoezi 65-69, tafuta hatua ya makutano ya kila jozi ya mistari ikiwa iko. Ikiwa haipo, onyesha kuwa hakuna hatua ya makutano.

65)$y=\dfrac{3}{4}x+1 \\ −3x+4y=12$

Jibu: hakuna hatua ya makutano

66)$2x−3y=12 \\ 5y+x=30$

67)$2x=y−3 \\ y+4x=15$

Jibu: $(2, 7)$

68)$x−2y+2=3 \\ x−y=3 $

69)$5x+3y=−65 \\ x−y=−5 $

Jibu: $(–10, –5)$

Upanuzi

70) Pata usawa wa mstari unaofanana na mstari$g(x)=−0.01x + 2.01$ kupitia hatua$(1, 2)$.

71) Pata equation ya mstari perpendicular kwa mstari$g(x)=−0.01x+2.01$ kupitia hatua$(1, 2)$.

Jibu: $y=100x−98$

Kwa mazoezi 72-73, tumia kazi$f(x)=−0.1x+200$ na$g(x)=20x+0.1$.

72) Pata hatua ya makutano ya mistari$f$ na$g$.

73) Ambapo ni$f(x)$ kubwa kuliko$g(x)?$ wapi ni$g(x)$ mkubwa kuliko$f(x)?$

Jibu: $x<\dfrac{1999}{201}x>\dfrac{1999}{201}$

Real-World Matumizi

74) Kampuni ya kukodisha gari inatoa mipango miwili ya kukodisha gari.

Mpango A:$\$30$ kwa$\$0.18$ siku na kwa maili
Mpango B:$\$50$ kwa siku na mileage ya bure isiyo na ukomo

Ni maili ngapi ungehitaji kuendesha gari kwa mpango B ili kukuokoa pesa?

75) Kampuni ya simu ya mkononi inatoa mipango miwili kwa dakika.

Mpango A:$\$20$ kwa mwezi na$\$1$ kwa kila maandiko mia moja.
Mpango B:$\$50$ kwa mwezi na maandiko ya bure ya ukomo.

Je! Unahitaji maandiko ngapi kutuma kwa mwezi kwa mpango B ili kukuokoa pesa?

Jibu: Chini ya$3000$ maandiko

76) Kampuni ya simu ya mkononi inatoa mipango miwili kwa dakika.

Mpango A:$\$15$ kwa mwezi na$\$2$ kwa kila$300$ maandiko.
Mpango B:$\$25$ kwa mwezi na$\$0.50$ kwa kila$100$ maandiko.

Je! Unahitaji maandiko ngapi kutuma kwa mwezi kwa mpango B ili kukuokoa pesa?

2.3 Mfano na Kazi za Mstari

Maneno

1) Eleza jinsi ya kupata kutofautiana kwa pembejeo katika tatizo la neno ambalo linatumia kazi ya mstari.

Jibu: Tambua kutofautiana kwa kujitegemea. Hii ni tofauti ambayo pato inategemea.

2) Eleza jinsi ya kupata kutofautiana kwa pato katika tatizo la neno ambalo linatumia kazi ya mstari.

3) Eleza jinsi ya kutafsiri thamani ya awali katika tatizo la neno ambalo linatumia kazi ya mstari.

Jibu: Kuamua thamani ya awali, pata pato wakati pembejeo ni sawa na sifuri.

4) Eleza jinsi ya kuamua mteremko katika tatizo la neno ambalo linatumia kazi ya mstari.

Kialjebra

5) Pata eneo la parallelogram iliyofungwa na$y$ mhimili$x=3$, mstari$f(x)=1+2x$, mstari, na mstari unaofanana na$f(x)$ kupitia (2, 7).

Jibu: $6$vitengo vya mraba

6) Pata eneo la pembetatu lililofungwa na$x$ -axis, mstari$f(x)=12–\dfrac{1}{3}x$, na mstari unaozingatia$f(x)$ kwamba hupita kupitia asili.

7) Pata eneo la pembetatu lililofungwa na$y$ -axis, mstari$f(x)=9–\dfrac{6}{7}x$, na mstari unaozingatia$f(x)$ kwamba hupita kupitia asili.

Jibu: $20.012$vitengo vya mraba

8) Pata eneo la parallelogram iliyofungwa na$x$ -axis$g(x)=2$, mstari$f(x)=3x$, mstari, na mstari unaofanana na$f(x)$ kupitia (6,1).

Kwa mazoezi 9-10, fikiria hali hii: Idadi ya wakazi wa mji imekuwa ikipungua kwa kiwango cha mara kwa mara. Mwaka 2010 idadi ya wakazi ilikuwa$5,900$. Kufikia mwaka 2012 idadi ya watu imeshuka$4,700$. Kudhani hali hii inaendelea.

9) Kutabiri idadi ya watu mwaka 2016.

Jibu: $2,300$

10) Tambua mwaka ambao idadi ya watu itafikia$0$.

Kwa mazoezi 11-12, fikiria hali hii: Idadi ya wakazi wa mji imeongezeka kwa kiwango cha mara kwa mara. Mwaka 2010 idadi ya wakazi ilikuwa$46,020$. Kufikia 2012 idadi ya watu iliongezeka hadi$52,070$. Kudhani hali hii inaendelea.

11) Kutabiri idadi ya watu mwaka 2016.

Jibu: $64,170$

12) Tambua mwaka ambao idadi ya watu itafikia$75,000$.

Kwa mazoezi 13-18, fikiria hali hii: mji ina idadi ya awali ya$75,000$. Inakua kwa kiwango cha mara kwa mara cha$2,500$ mwaka kwa$5$ miaka.

13) Kupata kazi linear kwamba mifano ya wakazi wa mji$P$ kama kazi ya mwaka$t$,, ambapo$t$ ni idadi ya miaka tangu mfano kuanza.

Jibu: $P(t)=75,000+2500t$

14) Pata uwanja unaofaa na upeo wa kazi$P$.

15) Kama kazi$P$ ni graphed, kupata na kutafsiri$x$ - na$y$ -intercepts.

Jibu: $(-30, 0)$Miaka thelathini kabla ya kuanza kwa mfano huu, mji hakuwa na. $(0, 75,000)$Awali, mji alikuwa na idadi ya watu$75,000$.

16) Ikiwa kazi$P$ imewekwa, tafuta na kutafsiri mteremko wa kazi.

17) Pato litafikia lini$100,000$?

Jibu: Miaka kumi baada ya mfano kuanza.

18) Je! Ni pato gani katika$12$ miaka ya mwaka tangu mwanzo wa mfano?

Kwa mazoezi 19-24, fikiria hali hii: Uzito wa mtoto mchanga ni$7.5$ paundi. Mtoto alipata pound moja kwa mwezi kwa mwaka wake wa kwanza.

19) Pata kazi ya mstari ambayo inafanana na uzito wa mtoto$W$ kama kazi ya umri wa mtoto, kwa miezi,$t$.

Jibu: $W(t)=7.5t+0.5$

20) Pata uwanja unaofaa na upeo wa kazi$W$.

21) Kama kazi$W$ ni graphed, kupata na kutafsiri$x$ - na$y$ -intercepts.

Jibu: $(−15,0)$:$x$ -Intercept si plausible seti ya data kwa mfano huu kwa sababu ina maana mtoto uzito$0$ paundi$15$ miezi kabla ya kuzaliwa. $(0, 7.5)$: Mtoto alipima$7.5$ paundi wakati wa kuzaliwa.

22) Ikiwa kazi$W$ imewekwa, tafuta na kutafsiri mteremko wa kazi.

23) Wakati gani mtoto uzito$10.4$ paundi?

Jibu: Katika$5.8$ miezi ya umri.

24) Ni pato gani wakati pembejeo ni$6.2$? Tafsiri jibu lako.

Kwa mazoezi 25-30, fikiria hali hii: Idadi ya watu wanaosumbuliwa na baridi ya kawaida katika miezi ya baridi ilipungua kwa kasi kwa$205$ kila mwaka kutoka 2005 hadi 2010. Mwaka 2005,$12,025$ watu waliteseka.

25) Pata kazi ya mstari ambayo inafanana na idadi ya watu wanaotokana na baridi ya kawaida$C$ kama kazi ya mwaka,$t$.

Jibu: $C(t)=12,025−205t$

26) Pata uwanja unaofaa na upeo wa kazi$C$.

27) Kama kazi$C$ ni graphed, kupata na kutafsiri$x$ - na$y$ -intercepts.

Jibu: $(58.7, 0)$: Katika takribani$59$ miaka, idadi ya watu wanaotokana na baridi ya kawaida itakuwa$0$. $(0,12,025)$: Awali kulikuwa na$12,025$ watu waliosumbuliwa na baridi ya kawaida.

28) Ikiwa kazi$C$ imewekwa, tafuta na kutafsiri mteremko wa kazi.

29) Pato litafikia lini$0$?

Jibu: $2064$

30) Katika mwaka gani idadi ya watu itakuwa$9,700$?

Picha

Kwa mazoezi 31-34, tumia grafu katika Kielelezo hapa chini, ambayo inaonyesha faida$y$, kwa maelfu ya dola, ya kampuni katika mwaka fulani,$t$, ambapo$t$ inawakilisha idadi ya miaka tangu 1980.

$alt$

31) Pata kazi ya mstari$y$, ambapo$y$ inategemea$t$, idadi ya miaka tangu 1980.

Jibu: $y=−2t+180$

32) Tafuta na kutafsiri$y$ -intercept.

33) Tafuta na kutafsiri$x$ -intercept.

Jibu: Mwaka 2070, faida ya kampuni itakuwa sifuri.

34) Pata na kutafsiri mteremko.

Kwa mazoezi 35-38, tumia grafu katika Kielelezo hapa chini, ambayo inaonyesha faida$y$, kwa maelfu ya dola, ya kampuni katika mwaka fulani,$t$, ambapo$t$ inawakilisha idadi ya miaka tangu 1980.

$alt$

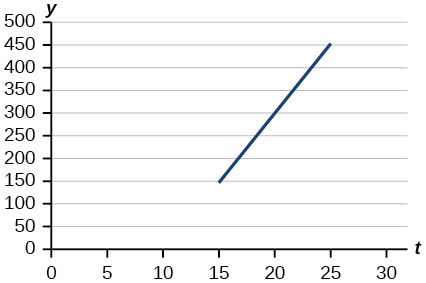
35) Pata kazi ya mstari$y$, ambapo$y$ inategemea$t$, idadi ya miaka tangu 1980.

Jibu: $y=30t−300$

36) Tafuta na kutafsiri$y$ -intercept.

37) Tafuta na kutafsiri$x$ -intercept.

Jibu: $(10, 0)$Mwaka 1990, faida ilipata faida ya sifuri.

38) Pata na kutafsiri mteremko.

Numeric

Kwa mazoezi 39-41, kutumia wastani maadili nyumbani katika Mississippi na Hawaii (kubadilishwa kwa mfumuko wa bei) inavyoonekana katika Jedwali hapa chini. Fikiria kwamba maadili ya nyumba yanabadilika kwa mstari.

Mwaka	Mississippi	Hawaii
1950	$25,200	$74,400
2000	$71,400	$272,700

39) Katika hali gani na maadili ya nyumbani yameongezeka kwa kiwango cha juu?

Jibu: Hawaii

40) Kama mwenendo huu walikuwa kuendelea, nini itakuwa wastani nyumbani thamani katika Mississippi katika 2010?

41) Ikiwa tunadhani mwenendo wa mstari ulikuwepo kabla ya 1950 na unaendelea baada ya 2000, maadili ya nyumba ya wastani ya nchi mbili yatakuwa (au yalikuwa) sawa katika mwaka gani? (Jibu inaweza kuwa ajabu.)

Jibu: Katika mwaka wa 1933

Kwa mazoezi 42-44, kutumia wastani maadili nyumbani katika Indiana na Alabama (kubadilishwa kwa mfumuko wa bei) inavyoonekana katika Jedwali hapa chini. Fikiria kwamba maadili ya nyumba yanabadilika kwa mstari.

Mwaka	Indiana	Alabama
1950	$37,700	$27,100
2000	$94,300	$85,100

42) Katika hali gani na maadili ya nyumbani kuongezeka kwa kiwango cha juu?

43) Kama mwenendo huu walikuwa kuendelea, nini itakuwa wastani nyumbani thamani katika Indiana katika 2010?

Jibu: $\$105,620$

44) Ikiwa tunadhani mwenendo wa mstari ulikuwepo kabla ya 1950 na unaendelea baada ya 2000, maadili ya nyumba ya wastani ya nchi mbili yatakuwa (au yalikuwa) sawa katika mwaka gani? (Jibu inaweza kuwa ajabu.)

Real-World Matumizi

45) Mwaka 2004, idadi ya shule ilikuwa$1001$. Kufikia 2008 idadi ya watu ilikuwa imeongezeka kwa$1697$. Tuseme idadi ya watu inabadilika linearly.

Idadi ya watu ilikua kiasi gani kati ya mwaka 2004 na 2008?
Ilichukua muda gani idadi ya watu kukua kutoka kwa$1001$ wanafunzi hadi$1697$ wanafunzi?
Ukuaji wa wastani wa idadi ya watu kwa mwaka ni nini?
Idadi ya watu ilikuwa nini katika mwaka wa 2000?
Kupata equation kwa idadi ya watu$P$,, ya$t$ miaka ya shule baada ya 2000.
Kutumia equation yako, kutabiri idadi ya watu wa shule katika 2011.

Jibu

$696$watu
$4$miaka
$174$watu kwa mwaka
$305$watu
$P(t)=305+174t$
$2219$watu

46) Mwaka 2003, idadi ya wakazi wa mji ilikuwa$1431$. Kufikia 2007 idadi ya watu ilikuwa imeongezeka hadi$2134$. Tuseme idadi ya watu inabadilika linearly.

Idadi ya watu ilikua kiasi gani kati ya mwaka 2003 na 2007?
Ilichukua muda gani idadi ya watu kukua kutoka kwa$1431$ watu hadi$2134$ watu?
Ukuaji wa wastani wa idadi ya watu kwa mwaka ni nini?
Idadi ya watu ilikuwa nini katika mwaka wa 2000?
Kupata equation kwa idadi ya watu,$P$ ya$t$ miaka ya mji baada ya 2000.
Kutumia equation yako, kutabiri idadi ya wakazi wa mji katika 2014.

47) Kampuni ya simu ina mpango wa kila mwezi wa mkononi ambapo mteja hulipa ada ya kila mwezi ya gorofa na kisha kiasi fulani cha fedha kwa dakika kutumika kwenye simu. Ikiwa mteja anatumia$410$ dakika, gharama ya kila mwezi itakuwa$\$71.50$. Ikiwa mteja anatumia$720$ dakika, gharama ya kila mwezi itakuwa$\$118$.

Tafsiri mteremko na$y$ -intercept ya equation.
Tumia equation yako ili kupata jumla ya gharama ya kila mwezi ikiwa$687$ dakika zinatumiwa.

Jibu

$C(x)=0.15x+10$
Malipo ya kila mwezi ya gorofa ni$\$10$ na kuna$\$0.15$ ada ya ziada kwa kila dakika ya ziada inayotumiwa
$\$113.05$

48) kampuni ya simu ina kila mwezi mpango wa data za mkononi ambapo mteja hulipa gorofa ada ya kila mwezi ya$\$10$ na kisha kiasi fulani cha fedha kwa megabyte (MB) ya data kutumika kwenye simu. Ikiwa mteja anatumia$20$ MB, gharama ya kila mwezi itakuwa$\$11.20$. Ikiwa mteja anatumia$130$ MB, gharama ya kila mwezi itakuwa$\$17.80$.

Tafsiri mteremko na$y$ -intercept ya equation.
Tumia equation yako ili kupata jumla ya gharama ya kila mwezi ikiwa$250$ MB hutumiwa.

49) Mwaka 1991, idadi ya watu katika mbuga ilipimwa kuwa$4,360$. Kufikia mwaka wa 1999, idadi ya watu ilipimwa tena kuwa$5,880$. Kudhani idadi ya watu inaendelea kubadilika linearly.

Je, mfano wako unatabiri idadi ya watu wa moose kuwa mwaka 2003?

Jibu

$P(t)=190t+4360$
$6640$kondoo

50) Mwaka 2003, idadi ya bunduki katika hifadhi ilipimwa kuwa$340$. Kufikia mwaka wa 2007, idadi ya watu ilipimwa tena kuwa$285$. Idadi ya watu hubadilika kwa mstari. Hebu pembejeo iwe miaka tangu 1990.

Je, mfano wako unatabiri idadi ya watu wa bunduki kuwa mwaka 2012?

51) Hifadhi ya Heliamu ya Shirikisho$16$ ilifanya takriban futi za ujazo bilioni za heliamu mwaka 2010 na inaharibiwa na$2.1$ futi za ujazo bilioni kila mwaka.

Mwaka 2015, hifadhi ya heliamu itakuwa nini?
Ikiwa kiwango cha kupungua haitabadilika, katika mwaka gani Hifadhi ya Helium ya Shirikisho itafutwa?

Jibu

$R(t)=16−2.1t$
$5.5$futi za ujazo bilioni
Katika mwaka 2017

52) Tuseme hifadhi ya mafuta duniani mwaka 2014 ni mapipa$1,820$ bilioni. Ikiwa, kwa wastani, hifadhi ya jumla inapungua kwa mapipa$25$ bilioni ya mafuta kila mwaka:

Miaka saba kuanzia sasa, hifadhi ya mafuta itakuwa nini?
Ikiwa kiwango ambacho hifadhi zinapungua ni mara kwa mara, hifadhi ya mafuta ya dunia itafutwa lini?

53) Wewe ni kuchagua kati ya mbili mipango mbalimbali kulipia kabla ya simu ya mkononi. Mpango wa kwanza unashutumu kiwango cha$26$ senti kwa dakika. Mpango wa pili unashutumu ada ya kila mwezi ya$\$19.95$ pamoja na$11$ senti kwa dakika. Je! Ungependa kutumia dakika ngapi kwa mwezi ili mpango wa pili uwe bora?

Jibu: Zaidi ya$133$ dakika

54) Unachagua kati ya makampuni mawili ya kuosha dirisha. Mashtaka ya kwanza$\$5$ kwa dirisha. Ya pili inadai ada ya msingi ya$\$40$ pamoja$\$3$ kwa kila dirisha. Je! Unahitaji madirisha ngapi kuwa na kampuni ya pili ili iwe bora?

55) Wakati wa kuajiriwa katika kazi mpya ya kuuza kujitia, unapewa chaguzi mbili za kulipa:

Chaguo A: Mshahara wa$\$17,000$ msingi wa mwaka na tume$12\%$ ya mauzo yako
Chaguo B: Mshahara wa$\$20,000$ msingi wa mwaka na tume$5\%$ ya mauzo yako

Kiasi gani kujitia bila haja ya kuuza kwa chaguo A kuzalisha mapato makubwa?

Jibu: Zaidi ya$\$42,857.14$ thamani ya kujitia

56) Unapoajiriwa katika kazi mpya ya kuuza umeme, unapewa chaguzi mbili za kulipa:

Chaguo A: Msingi mshahara$\$14,000$ wa mwaka na tume$10\%$ ya mauzo yako

Chaguo B: Msingi mshahara$\$19,000$ wa mwaka na tume$4\%$ ya mauzo yako

Kiasi gani cha umeme ungehitaji kuuza kwa chaguo A kuzalisha kipato kikubwa?

57) Unapoajiriwa katika kazi mpya ya kuuza umeme, unapewa chaguzi mbili za kulipa:

Chaguo A: Msingi mshahara$\$20,000$ wa mwaka na tume$12\%$ ya mauzo yako

Chaguo B: Msingi mshahara$\$26,000$ wa mwaka na tume$3\%$ ya mauzo yako

Kiasi gani cha umeme ungehitaji kuuza kwa chaguo A kuzalisha kipato kikubwa?

Jibu: $\$66,666.67$

58) Unapoajiriwa katika kazi mpya ya kuuza umeme, unapewa chaguzi mbili za kulipa:

Chaguo A: Msingi mshahara$\$10,000$ wa mwaka na tume$9\%$ ya mauzo yako

Chaguo B: Msingi mshahara$\$20,000$ wa mwaka na tume$4\%$ ya mauzo yako

Kiasi gani cha umeme ungehitaji kuuza kwa chaguo A kuzalisha kipato kikubwa?

2.4 Kufaa Mifano ya Linear kwa Data

Maneno

1) Eleza maana gani ikiwa kuna kuvunjika kwa mfano wakati wa kutumia mfano wa mstari.

Jibu: Wakati mtindo wetu hautumiki tena, baada ya thamani fulani katika kikoa, mfano yenyewe haukubali.

2) Ufuatiliaji ni nini wakati wa kutumia mfano wa mstari?

3) Je, ni extrapolation gani wakati wa kutumia mfano wa mstari?

Jibu: Tunatabiri thamani nje ya kikoa na data mbalimbali.

4) Eleza tofauti kati ya mgawo mzuri na hasi uwiano.

5) Eleza jinsi ya kutafsiri thamani kamili ya mgawo wa uwiano.

Jibu: Nambari ya karibu ni$1$, chini ya kutawanyika data, karibu idadi ni$0$, zaidi kutawanyika data.

Kialjebra

6) Ukandamizaji uliendeshwa ili kuamua kama kuna uhusiano kati ya masaa ya TV yaliyoangaliwa kwa siku (x) na idadi ya kukaa mtu anayeweza kufanya (y). Matokeo ya regression hutolewa hapa chini. Tumia hii kutabiri idadi ya kukaa-ups mtu ambaye anaangalia$11$ masaa ya TV anaweza kufanya.

\[\begin{array}{l}{y=a x+b} \\ {a=-1.341} \\ {b=32.234} \\ {r=-0.896}\end{array}\nonumber\]

7) Ukandamizaji uliendeshwa ili kuamua kama kuna uhusiano kati ya kipenyo cha mti ($x$, kwa inchi) na umri wa mti ($y$, kwa miaka). Matokeo ya regression hutolewa hapa chini. Tumia hii kutabiri umri wa mti wenye$10$ inchi za kipenyo. \[\begin{array}{l}{y=a x+b} \\ {a=6.301} \\ {b=-1.044} \\ {r=-0.970}\end{array}\nonumber\]

Jibu: $61.966$miaka

Kwa mazoezi 8-11, futa njama ya kutawanya kwa data iliyotolewa. Je, data inaonekana kuwa linearly kuhusiana?

0	2	4	6	8	10
—22	—19	—15	—11	—6	—2

1	2	3	4	5	6
46	50	59	75	100	136

Jibu: Hapana

10)

100	250	300	450	600	750
12	12.6	13.1	14	14.5	15.2

11)

1	3	5	7	9	11
1	9	28	65	125	216

Jibu: Hapana

12) Kwa data zifuatazo, futa njama ya kutawanya. Ikiwa tulitaka kujua lini idadi ya watu ingeweza kufikia$15,000$, je, jibu litahusisha ufuatiliaji au extrapolation? Eyeball line, na makisio jibu.

Mwaka	Idadi ya watu
1990	11,500
1995	12,100
2000	12,700
2005	13,000
2010	13,750

13) Kwa data zifuatazo, futa njama ya kutawanya. Ikiwa tulitaka kujua wakati joto lingefikia$28^{\circ} F$, je, jibu litahusisha ufuatiliaji au extrapolation? Eyeball mstari na makisio jibu.

Joto, °F	16	18	20	25	30
Muda, sekunde	46	50	54	55	62

Jibu: Ufuatiliaji. Kuhusu$60° F$.

Picha

Kwa mazoezi 14-17, mechi ya kila scatterplot na moja ya mahusiano manne maalum katika Kielelezo ab na Kielelezo cd.

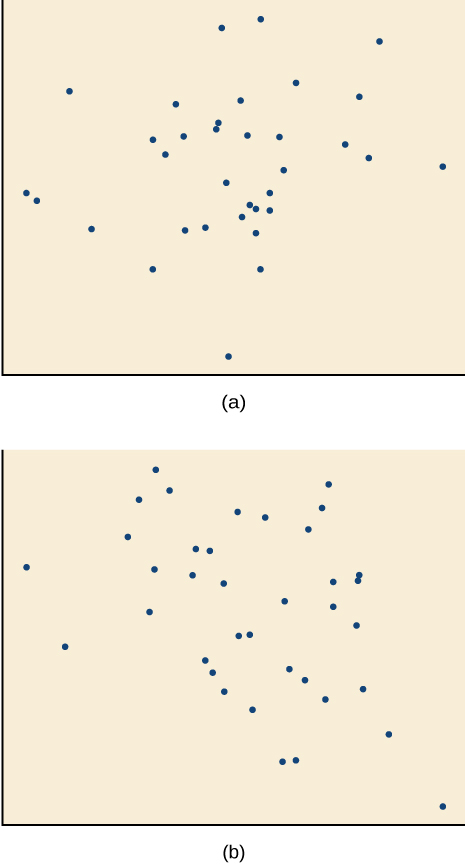
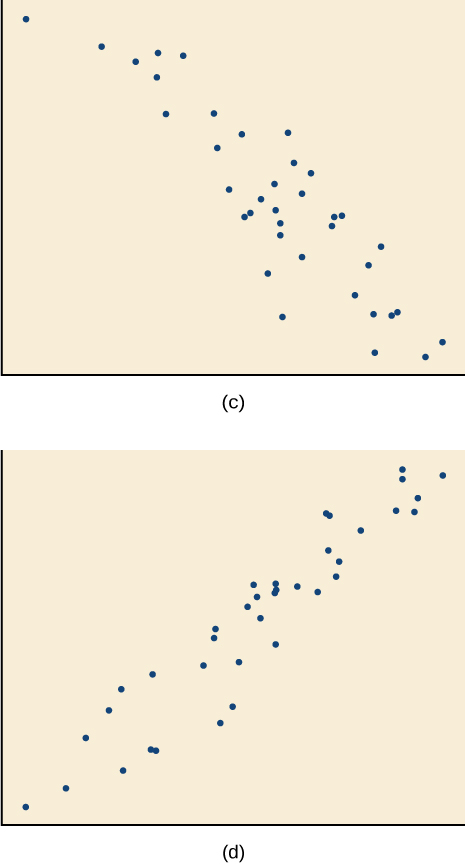
14)$r=0.95$

15)$r=−0.89$

Jibu: C

16)$r=0.26$

17)$r=−0.39$

Jibu: B

Kwa mazoezi 18-21, futa mstari bora zaidi kwa data iliyopangwa.

18)

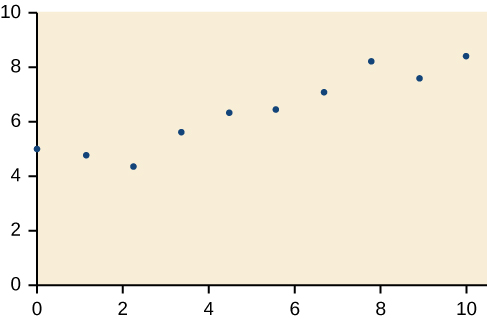
$CNX_Precalc_02_04_02.jpg$

19)

$alt$

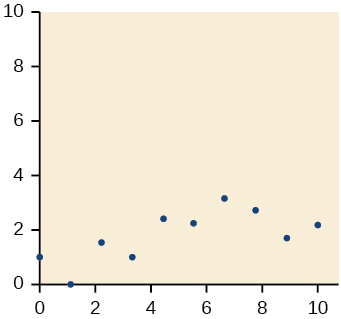
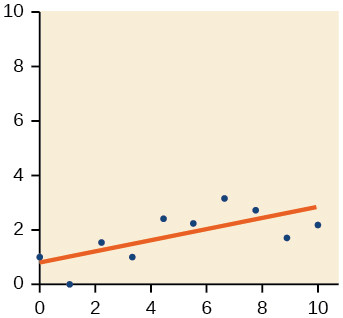
Jibu: $CNX_Precalc_Figure_02_04_205.jpg$

20)

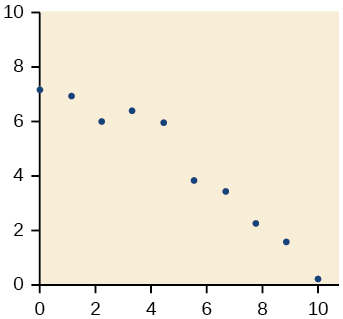
$CNX_Precalc_Figure_02_04_206.jpg$

21)

$alt$

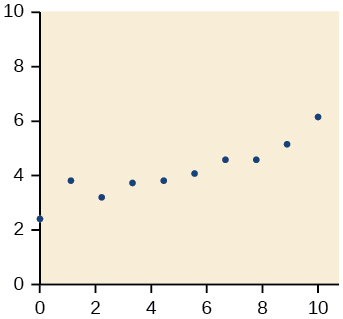
Jibu: $alt$

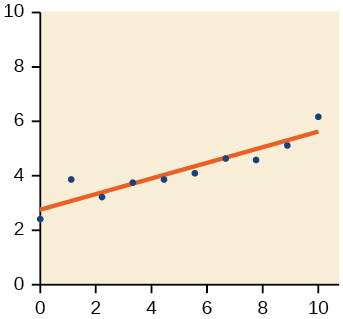
Numeric

22) Sensa ya Marekani inafuatilia asilimia ya watu wa$25$ miaka au zaidi ambao ni wahitimu wa chuo. Takwimu hizo kwa miaka kadhaa zinatolewa katika Jedwali hapa chini. Kuamua kama mwenendo unaonekana mstari. Ikiwa ndivyo, na kuchukua mwenendo unaendelea, katika mwaka gani asilimia itazidi$35\%$?

Mwaka	Asilimia Wahitimu
1990	21.3
1992	21.4
1994	22.2
1996	23.6
1998	24.4
2000	25.6
2002	26.7
2004	27.7
2006	28
2008	29.4

23) Uagizaji wa divai ya Marekani (katika hektoliters) kwa miaka kadhaa hutolewa katika Jedwali. Kuamua kama mwenendo unaonekana mstari. Kama ni hivyo, na kuchukua mwenendo inaendelea, katika mwaka gani itakuwa nje kisichozidi$12,000$ hectoliters?

Mwaka	Uagizaji
1992	2665
1994	2688
1996	3565
1998	4129
2000	4584
2002	5655
2004	6549
2006	7950
2008	8487
2009	9462

Jibu: Ndiyo, mwenendo inaonekana linear kwa sababu$r=0.985$ na itazidi$12,000$ karibu katikati ya mwaka, 2016,$24.6$ miaka tangu 1992.

24) Jedwali linaonyesha mwaka na idadi ya watu wasio na kazi katika mji fulani kwa miaka kadhaa. Kuamua kama mwenendo unaonekana mstari. Ikiwa ndivyo, na kuchukua mwenendo unaendelea, katika mwaka gani idadi ya wasio na ajira itafikia$5$?

Mwaka	Idadi Ajira
1990	750
1992	670
1994	650
1996	605
1998	550
2000	510
2002	460
2004	420
2006	380
2008	320

Teknolojia

Kwa mazoezi 25-31, tumia kila seti ya data ili kuhesabu mstari wa kurudi nyuma kwa kutumia calculator au chombo kingine cha teknolojia, na ueleze mgawo wa uwiano kwa maeneo ya$3$ decimal ya usahihi.

25)

$x$	8	15	26	31	56
$y$	23	41	53	72	103

Jibu: $y=1.640x+13.800, r=0.987$

26)

$x$	5	7	10	12	15
$y$	4	12	17	22	24

27)

$x$	$y$	$x$	$y$
\ (x\) ">3	\ (y\) "> 21.9	\ (x\) ">11	\ (y\) ">15.76
\ (x\) ">4	\ (y\) "> 22.22	\ (x\) ">12	\ (y\) ">13.68
\ (x\) "> 5	\ (y\) "> 22.74	\ (x\) ">13	\ (y\) ">14.1
\ (x\) ">6	\ (y\) "> 22.26	\ (x\) ">14	\ (y\) ">14.02
\ (x\) ">7	\ (y\) "> 20.78	\ (x\) ">15	\ (y\) ">11.94
\ (x\) ">8	\ (y\) ">17.6	\ (x\) ">16	\ (y\) ">12.76
\ (x\) ">9	\ (y\) ">16.52	\ (x\) ">17	\ (y\) ">11.28
\ (x\) ">10	\ (y\) "> 18.54	\ (x\) ">18	\ (y\) "> 9.1

Jibu: $y=−0.962x+26.86, r=−0.965$

28)

$x$	$y$
\ (x\) ">4	\ (y\) ">44.8
\ (x\) "> 5	\ (y\) ">43.1
\ (x\) ">6	\ (y\) ">38.8
\ (x\) ">7	\ (y\) ">39
\ (x\) ">8	\ (y\) ">38
\ (x\) ">9	\ (y\) ">32.7
\ (x\) ">10	\ (y\) ">30.1
\ (x\) ">11	\ (y\) "> 29.3
\ (x\) ">12	\ (y\) ">27
\ (x\) ">13	\ (y\) "> 25.8

29)

$x$	$y$
\ (x\) ">21	\ (y\) ">17
\ (x\) ">25	\ (y\) ">11
\ (x\) ">30	\ (y\) "> 2
\ (x\) ">31	\ (y\) ">-1
\ (x\) ">40	\ (y\) ">18-18
\ (x\) ">50	\ (y\) "> -40

Jibu: $y=−1.981x+60.197; r=−0.998$

30)

$x$	$y$
\ (x\) ">100	\ (y\) "> 2000
\ (x\) "> 80	\ (y\) ">1798
\ (x\) ">60	\ (y\) ">1589
\ (x\) ">55	\ (y\) ">1580
\ (x\) ">40	\ (y\) ">1390
\ (x\) ">20	\ (y\) ">1202

31)

$x$	$y$
\ (x\) "> 900	\ (y\) ">70
\ (x\) ">988	\ (y\) "> 80
\ (x\) "> 1000	\ (y\) ">82
\ (x\) ">1010	\ (y\) ">84
\ (x\) ">1200	\ (y\) ">105
\ (x\) "> 1205	\ (y\) ">108

Jibu: $y=0.121x−38.841, r=0.998$

Upanuzi

32) Grafu$f(x)=0.5x+10$. Chagua seti ya jozi$5$ zilizoamriwa kwa kutumia pembejeo$x=−2, 1, 5, 6, 9$ na utumie regression ya mstari ili kuthibitisha kuwa kazi inafaa kwa data.

33) Grafu$f(x)=−2x−10$. Chagua seti ya jozi$5$ zilizoamriwa kwa kutumia pembejeo$x=−2, 1, 5, 6, 9$ na utumie regression ya mstari ili kuthibitisha kazi.

Jibu: $(−2,−6),(1,−12),(5,−20),(6,−22),(9,−28); y=−2x−10$

Kwa mazoezi 34-36, fikiria hali hii: Faida ya kampuni ilipungua kwa kasi zaidi ya kipindi cha miaka kumi. zifuatazo kuamuru jozi inaonyesha dola na idadi ya vitengo kuuzwa katika mamia na faida katika maelfu ya zaidi ya miaka kumi span, (idadi ya vitengo kuuzwa, faida) kwa miaka maalum kumbukumbu:

\[(46, 1,600), (48, 1,550), (50, 1,505), (52, 1,540), (54, 1,495) \nonumber\]

34) Tumia regression linear kuamua kazi$P$ ambapo faida katika maelfu ya dola inategemea idadi ya vitengo kuuzwa katika mamia.

35) Tafuta sehemu ya kumi ya karibu na ufafanue$x$ -intercept.

Jibu: $(189.8,0)$Ikiwa$18,980$ vitengo vinauzwa, kampuni hiyo itakuwa na faida ya dola za sifuri.

36) Tafuta sehemu ya kumi ya karibu na ufafanue$y$ -intercept.

Real-World Matumizi

Kwa mazoezi 37-38, fikiria hali hii: Idadi ya wakazi wa jiji iliongezeka kwa kasi zaidi ya kipindi cha miaka kumi. Jozi zifuatazo zilizoamriwa zinaonyesha idadi ya watu na mwaka juu ya muda wa miaka kumi, (idadi ya watu, mwaka) kwa miaka maalum iliyoandikwa:

\[(2500, 2000), (2650, 2001), (3000, 2003), (3500, 2006), (4200, 2010) \nonumber \]

37) Tumia regression linear kuamua kazi$y$, ambapo mwaka inategemea idadi ya watu. Pande zote kwa maeneo matatu ya usahihi.

Jibu: $y=0.00587x+1985.41$

38) Kutabiri wakati idadi ya watu hit$8,000$.

Kwa mazoezi 39-40, fikiria hali hii: Faida ya kampuni iliongezeka kwa kasi zaidi ya kipindi cha miaka kumi. Jozi zifuatazo zilizoamriwa zinaonyesha idadi ya vitengo vinavyouzwa kwa mamia na faida kwa maelfu ya zaidi ya kipindi cha miaka kumi, (idadi ya vitengo vilivyouzwa, faida) kwa miaka maalum iliyoandikwa:

\[(46, 250), (48, 305), (50, 350), (52, 390), (54, 410) \nonumber \]

39) Tumia regression linear kuamua kazi$y$, ambapo faida katika maelfu ya dola inategemea idadi ya vitengo kuuzwa katika mamia.

Jibu: $y=20.25x−671.5$

40) Kutabiri wakati faida itazidi dola milioni moja.

Kwa mazoezi 41-42, fikiria hali hii: Faida ya kampuni ilipungua kwa kasi zaidi ya kipindi cha miaka kumi. Jozi zifuatazo zilizoamriwa zinaonyesha dola na idadi ya vitengo vinavyouzwa kwa mamia na faida kwa maelfu ya kipindi cha miaka kumi (idadi ya vitengo vilivyouzwa, faida) kwa miaka maalum iliyoandikwa:

\[(46, 250), (48, 225), (50, 205), (52, 180), (54, 165) \nonumber\]

41) Tumia regression linear kuamua kazi$y$, ambapo faida katika maelfu ya dola inategemea idadi ya vitengo kuuzwa katika mamia.

Jibu: $y=−10.75x+742.50$

42) Kutabiri wakati faida itakuwa kuzamisha chini ya$\$25,000$ kizingiti.

\(x\)	0	5	10	15
\(h(x)\)	5	30	105	230

\(x\)	0	5	10	15
\(f(x)\)	—5	20	45	70

\(x\)	5	10	20	25
\(k(x)\)	28	13	58	73

\(x\)	2	4	6	8
\(f(x)\)	—4	16	36	56