2.4: Mifano ya Linear inayofaa kwa Data

Malengo ya kujifunza

• Chora na kutafsiri michoro kuwatawanya.
• Tumia matumizi ya graphing ili kupata mstari wa kufaa bora.
• Tofautisha kati ya mahusiano ya mstari na yasiyo ya kawaida.
• Fanya mstari wa kurudi nyuma kwa seti ya data na utumie mfano wa mstari ili utabiri.

Profesa anajaribu kutambua mwenendo kati ya alama ya mwisho ya mtihani. Darasa lake lina mchanganyiko wa wanafunzi, hivyo anashangaa kama kuna uhusiano wowote kati ya umri na alama za mtihani wa mwisho. Njia moja kwa ajili yake kuchambua alama ni kwa kuunda mchoro unaohusiana na umri wa kila mwanafunzi kwa alama ya mtihani iliyopokelewa. Katika sehemu hii, tutachunguza mchoro mmoja unaojulikana kama njama ya kuwatawanya.

Kuchora na Kutafsiri Viwanja vya Ku

Mpango wa kuwatawanya ni grafu ya pointi zilizopangwa ambazo zinaweza kuonyesha uhusiano kati ya seti mbili za data. Kama uhusiano ni kutoka mfano linear, au mfano kwamba ni karibu linear, profesa anaweza kutekeleza hitimisho kwa kutumia ujuzi wake wa kazi linear. Kielelezo\(\PageIndex{1}\) inaonyesha sampuli kutawanya njama.

Kielelezo\(\PageIndex{1}\): njama kuwatawanya ya umri na vigezo mwisho mtihani alama

Kumbuka njama hii kuwatawanya haionyeshi uhusiano linear. Pointi hazionekani kufuata mwenendo. Kwa maneno mengine, haionekani kuwa na uhusiano kati ya umri wa mwanafunzi na alama kwenye mtihani wa mwisho.

Mfano\(\PageIndex{1}\): Using a Scatter Plot to Investigate Cricket Chirps

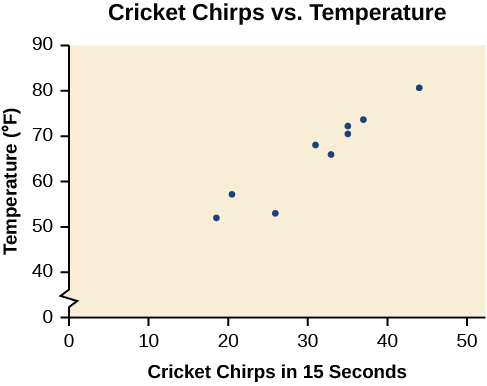
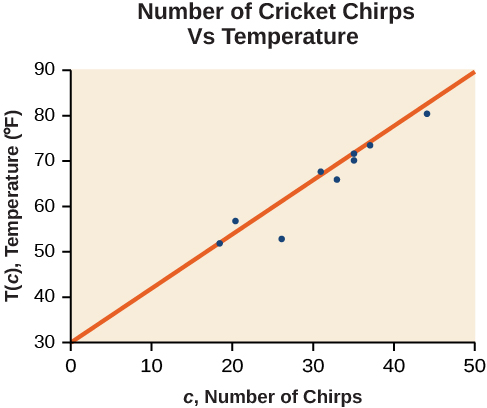
Jedwali linaonyesha idadi ya chirps za kriketi katika sekunde 15, kwa joto tofauti za hewa, kwa digrii Fahrenheit [1]. Plot data hii, na kuamua kama data inaonekana kuwa linearly kuhusiana.

Jedwali\(\PageIndex{1}\)

Chirps	44	35	20.4	33	31	35	18.5	37	26
Joto	80.5	70.5	57	66	68	72	52	73.5	53

Suluhisho

Kupanga data hii, kama inavyoonyeshwa kwenye Kielelezo\(\PageIndex{2}\) inaonyesha kwamba kunaweza kuwa na mwenendo. Tunaweza kuona kutokana na mwenendo katika data kwamba idadi ya chirps huongezeka kadiri joto linavyoongezeka. Mwelekeo unaonekana kuwa sawa na mstari, ingawa hakika sio kikamilifu.

Kielelezo\(\PageIndex{2}\): Ukandamizaji wa mstari kwa ujumla ni chanya.

Kupata Line ya Fit Bora

Mara baada ya kutambua haja ya kazi linear kwa mfano kwamba data, asili kufuatilia swali ni “nini kwamba kazi linear?” Njia moja ya takriban kazi yetu linear ni mchoro line kwamba inaonekana bora fit data. Kisha tunaweza kupanua mstari mpaka tunaweza kuthibitisha y-intercept. Tunaweza takriban mteremko wa mstari kwa kupanua mpaka tunaweza kukadiria\(\frac{\text{rise}}{\text{run}}\).

Mfano\(\PageIndex{2}\): Finding a Line of Best Fit

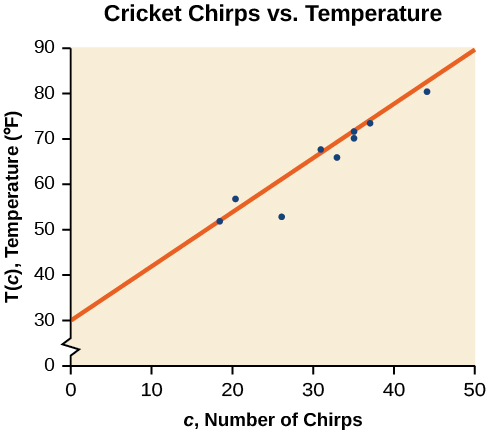
Kupata kazi linear kwamba inafaa data katika Jedwali\(\PageIndex{1}\) na “eyeballing” line kwamba inaonekana fit.

Suluhisho

Kwenye grafu, tunaweza kujaribu sketching line.

Kutumia pointi za kuanzia na za mwisho za mstari wetu uliotolewa, pointi\((0, 30)\) na\((50, 90)\), grafu hii ina mteremko wa

\[m=\dfrac{60}{50}=1.2\]

na y-intercept saa 30. Hii inatoa equation ya

\[T(c)=1.2c+30\]

ambapo\(c\) ni idadi ya chirps katika sekunde 15, na\(T(c)\) ni joto katika digrii Fahrenheit. Equation kusababisha ni kuwakilishwa katika Kielelezo\(\PageIndex{3}\).

Kielelezo\(\PageIndex{3}\): Kusambaza njama, kuonyesha mstari wa fit bora.

Uchambuzi

Equation hii linear kisha inaweza kutumika kwa takriban majibu ya maswali mbalimbali tunaweza kuuliza kuhusu mwenendo.

Kutambua Ufuatiliaji au Extrapolation

Wakati data kwa mifano mingi haiingii kikamilifu kwenye mstari, equation ni nadhani yetu bora kuhusu jinsi uhusiano utakavyoishi nje ya maadili ambayo tuna data. Tunatumia mchakato unaojulikana kama tafsiri wakati sisi kutabiri thamani ndani ya uwanja na aina mbalimbali ya data. Mchakato wa extrapolation hutumiwa wakati tunatabiri thamani nje ya uwanja na data mbalimbali.

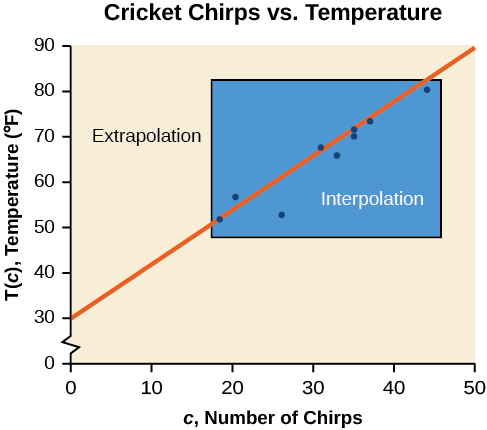
Kielelezo\(\PageIndex{4}\) kulinganisha michakato miwili kwa ajili ya data kriket-chirp kushughulikiwa katika Mfano\(\PageIndex{2}\). Tunaweza kuona kwamba tafsiri itatokea kama tulitumia mfano wetu kutabiri halijoto wakati maadili ya chirps yana kati ya 18.5 na 44. Extrapolation ingekuwa kutokea kama sisi kutumika mfano wetu kutabiri joto wakati maadili kwa chirps ni chini ya 18.5 au zaidi ya 44.

Kuna tofauti kati ya kufanya utabiri ndani ya kikoa na maadili mbalimbali ambayo tuna data na nje ya uwanja huo na upeo. Kutabiri thamani nje ya uwanja na upeo una mapungufu yake. Wakati mfano wetu hautumiki tena baada ya hatua fulani, wakati mwingine huitwa kuvunjika kwa mfano. Kwa mfano, kutabiri kazi ya gharama kwa kipindi cha miaka miwili inaweza kuhusisha kuchunguza data ambapo pembejeo ni wakati katika miaka na pato ni gharama. Lakini kama sisi kujaribu extrapolate gharama wakati\(x=50\), kwamba ni katika miaka 50, mfano bila kuomba kwa sababu hatuwezi akaunti kwa sababu miaka hamsini katika siku zijazo.

Kielelezo\(\PageIndex{4}\): Ufuatiliaji hutokea ndani ya uwanja na aina mbalimbali ya data zinazotolewa wakati extrapolation hutokea nje.

Ufuatiliaji na Extrapolation

Mbinu tofauti za kufanya utabiri hutumiwa kuchambua data.

• Njia ya extrapolation inahusisha kutabiri thamani nje ya uwanja na/au data mbalimbali.
• Uharibifu wa mfano hutokea wakati ambapo mtindo hautumiki tena.

Mfano\(\PageIndex{3}\): Understanding Interpolation and Extrapolation

Tumia data ya kriketi kutoka Jedwali\(\PageIndex{1}\) ili kujibu maswali yafuatayo:

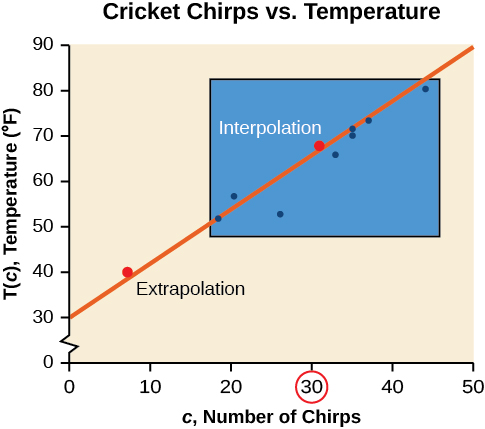
1. Je, utabiri wa joto wakati crickets ni chirping mara 30 katika sekunde 15 kuwa interpolation au extrapolation? Kufanya utabiri, na kujadili kama ni busara.
2. Je utabiri idadi ya chirps crickets kufanya katika digrii 40 kuwa interpolation au extrapolation? Kufanya utabiri, na kujadili kama ni busara.

Suluhisho

a. idadi ya chirps katika data zinazotolewa mbalimbali kutoka 18.5 kwa 44. Utabiri katika chirps 30 kwa sekunde 15 ni ndani ya uwanja wa data yetu, hivyo itakuwa tafsiri. Kutumia mfano wetu:

\[\begin{align} T(30)&=30+1.2(30) \\ &=66 \text{ degrees} \end{align}\]

Kulingana na data tuliyo nayo, thamani hii inaonekana kuwa ya busara.
b Maadili ya joto yanatofautiana kutoka 52 hadi 80.5. Kutabiri idadi ya chirps katika digrii 40 ni extrapolation kwa sababu 40 ni nje ya mbalimbali ya data yetu. Kutumia mfano wetu:

\[\begin{align} 40&=30+1.2c \\ 10&=1.2c \\ c&\approx8.33 \end{align}\]

Tunaweza kulinganisha mikoa ya kutafsiri na extrapolation kutumia Kielelezo\(\PageIndex{5}\).

Kielelezo\(\PageIndex{5}\): Kuwatawanya njama, kuonyesha mstari wa fit bora na ambapo tafsiri na extrapolation hutokea.

Uchambuzi

Mfano wetu anatabiri crickets ingekuwa chirp mara 8.33 katika sekunde 15. Ingawa hii inaweza kuwa inawezekana, hatuna sababu ya kuamini mfano wetu ni halali nje ya uwanja na upeo. Kwa kweli, kwa ujumla crickets kuacha chirping kabisa chini ya digrii 50.

Zoezi\(\PageIndex{1}\)

Kwa mujibu wa data kutoka Jedwali\(\PageIndex{1}\), ni joto gani tunaweza kutabiri ni kama tulihesabu chirps 20 katika sekunde 15?

Suluhisho

54°F

Kutafuta Line ya Fit Bora Kutumia Huduma ya Graphing

Wakati eyeballing line kazi sababu vizuri, kuna mbinu za takwimu kwa ajili ya kufaa mstari wa data kwamba kupunguza tofauti kati ya mstari na data maadili [2]. Mbinu moja hiyo inaitwa angalau mraba regression na inaweza kuhesabiwa na calculators wengi graphing, spreadsheet programu, programu ya takwimu, na wengi calculators mtandao mtandao [3]. Angalau mraba regression ni njia moja ya kuamua mstari kwamba bora inafaa data, na hapa sisi kutaja njia hii kama linear regression.

Kutokana na data ya pembejeo na matokeo yanayofanana kutoka kwa kazi ya mstari, pata mstari bora unaofaa kwa kutumia regression linear.

1. Ingiza pembejeo katika Orodha ya 1 (L1).
2. Ingiza pato katika Orodha ya 2 (L2).
3. Kwenye matumizi ya graphing, chagua Regression Linear (LinReg).

Mfano\(\PageIndex{4}\): Finding a Least Squares Regression Line

Find angalau mraba regression line kutumia data kriket-chirp katika Jedwali\(\PageIndex{1}\).

Suluhisho

Ingiza pembejeo (chirps) katika Orodha ya 1 (L1).
Ingiza pato (joto) katika Orodha ya 2 (L2). Angalia Jedwali\(\PageIndex{2}\).

Jedwali\(\PageIndex{2}\)

L1	44	35	20.4	33	31	35	18.5	37	26
L2	80.5	70.5	57	66	68	72	52	73.5	53

Kwenye matumizi ya graphing, chagua Regression Linear (LinReg). Kutumia data ya kriketi ya chirp kutoka mapema, na teknolojia tunapata equation:

\[T(c)=30.281+1.143c\]

Uchambuzi

Kumbuka kwamba mstari huu ni sawa kabisa na equation sisi “eyeballed” lakini lazima fit data bora. Angalia pia kwamba kutumia equation hii ingebadilisha utabiri wetu kwa joto wakati wa kusikia chirps 30 katika sekunde 15 kutoka digrii 66 hadi:

\[\begin{align} T(30)&=30.281+1.143(30) \\ &=64.571 \\ &\approx 64.6 \text{ degrees} \end{align}\]

Grafu ya njama ya kuwatawanya na mstari mdogo wa regression ya mraba inavyoonyeshwa kwenye Mchoro\(\PageIndex{6}\).

Kielelezo\(\PageIndex{6}\): Kusambaza njama, kuonyesha mstari wa fit bora.

Je! Kutakuwa na kesi ambapo mistari miwili tofauti itatumika kama inafaa zaidi kwa data?

Hapana. Kuna moja tu bora fit line.

Kutofautisha Kati ya Mifano ya Mstari na isiyo ya

Kama tulivyoona hapo juu na mfano wa kriket-chirp, data fulani inaonyesha mwenendo mkali wa mstari, lakini data nyingine, kama alama za mwisho za mtihani zilizopangwa kwa umri, ni wazi zisizo za kawaida. Wengi calculators na programu ya kompyuta pia inaweza kutupa na uwiano mgawo, ambayo ni kipimo cha jinsi karibu line inafaa data. Wengi graphing calculators zinahitaji user kurejea” uchunguzi juu ya” uteuzi kupata uwiano mgawo, ambayo wanahisabati studio kama\(r\). Mgawo wa uwiano hutoa njia rahisi ya kupata wazo la jinsi karibu na mstari data huanguka.

Tunapaswa kuhesabu mgawo wa uwiano tu kwa data inayofuata muundo wa mstari au kuamua kiwango ambacho kuweka data ni mstari. Ikiwa data inaonyesha muundo usio na mstari, mgawo wa uwiano wa kurudi nyuma kwa mstari hauna maana. Ili kupata hisia kwa uhusiano kati ya thamani ya\(r\) na grafu ya data, Kielelezo\(\PageIndex{7}\) inaonyesha baadhi ya seti kubwa data na coefficients yao uwiano. Kumbuka, kwa viwanja vyote, mhimili usio na usawa unaonyesha pembejeo na mhimili wima unaonyesha pato.

Kielelezo\(\PageIndex{7}\): Ilipanga data na kuhusiana uwiano coefficients. (mikopo: “DenisBoigelot,” Wikimedia Commons)

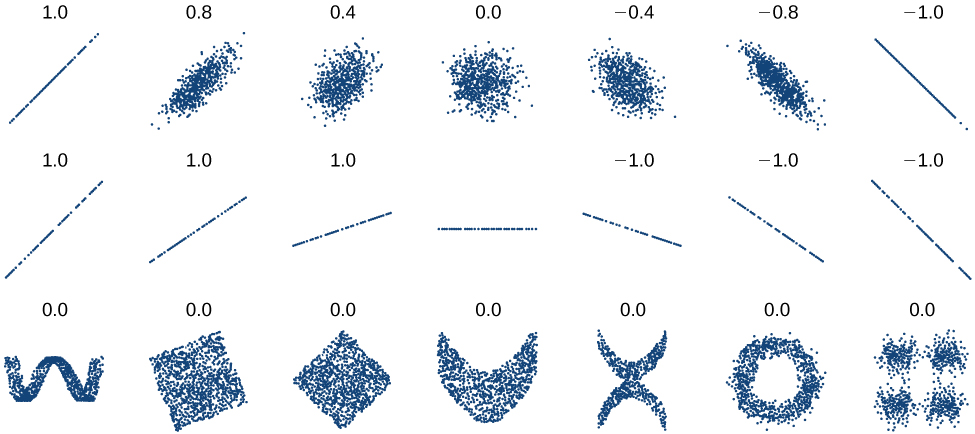
Mgawo wa uwiano

Mgawo wa uwiano ni thamani\(r\),, kati ya -1 na 1.

• \(r>0\)inaonyesha uhusiano mzuri (kuongezeka)
• \(r<0\)inaonyesha uhusiano mbaya (kupungua)
• Thamani ya karibu ni 0, data iliyoenea zaidi.
• Thamani ya karibu ni ya 1 au -1, chini ya kutawanyika data ni.

Mfano\(\PageIndex{5}\): Finding a Correlation Coefficient

Tumia mgawo wa uwiano wa data ya kriket-chirp katika Jedwali\(\PageIndex{1}\).

Suluhisho

Kwa sababu data inaonekana kufuata muundo linear, tunaweza kutumia teknolojia kuhesabu\(r\). Ingiza pembejeo na matokeo yanayofanana na uchague Ukandamizaji wa Linear. Calculator pia itakupa mgawo wa uwiano,\(r=0.9509\). Thamani hii ni karibu sana na 1, ambayo inaonyesha uhusiano mkubwa wa mstari.

Kumbuka: Kwa baadhi ya mahesabu, Diagnostics lazima igeuzwe “juu” ili kupata mgawo wa uwiano wakati regression linear inafanyika: [2] > [0] > [alpha] [x-1], kisha tembea kwa DIAGNOSTICSON.

Kutabiri kwa Mstari wa Regression

Mara tu tunapoamua kuwa seti ya data ni mstari kwa kutumia mgawo wa uwiano, tunaweza kutumia mstari wa kurudi nyuma ili kufanya utabiri. Kama tulivyojifunza hapo juu, mstari wa kurudi nyuma ni mstari ulio karibu na data katika njama ya kuwatawanya, ambayo ina maana kwamba mstari mmoja tu ni sawa na data.

Mfano\(\PageIndex{6}\): Using a Regression Line to Make Predictions

Matumizi ya petroli nchini Marekani yameongezeka kwa kasi. Data ya matumizi kutoka 1994 hadi 2004 inavyoonekana katika Jedwali\(\PageIndex{3}\). Kuamua kama mwenendo ni mstari, na ikiwa ni hivyo, pata mfano wa data. Kutumia mfano kutabiri matumizi ya mwaka 2008.

Jedwali\(\PageIndex{3}\)

Mwaka	'94	'95	'96	'97	'98	'99	'00	'01	'02	'03	'04
Matumizi (mabilioni ya galoni)	113	116	118	119	123	125	126	128	131	133	136

Mpango wa kuwatawanya wa data, ikiwa ni pamoja na mstari mdogo wa kurudi nyuma, umeonyeshwa kwenye Kielelezo\(\PageIndex{8}\).

Kielelezo\(\PageIndex{8}\): Kusambaza njama, kuonyesha mstari wa fit bora.

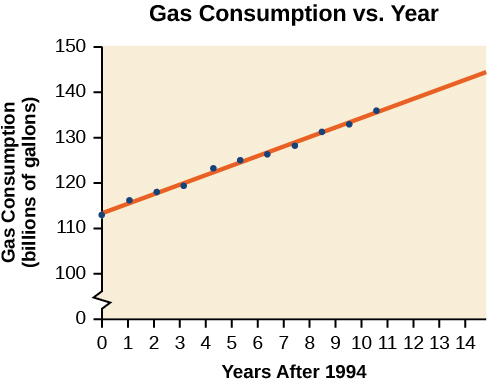
Tunaweza kuanzisha mpya pembejeo variable,\(t\), anayewakilisha miaka tangu 1994.

angalau mraba regression equation ni:

\[C(t)=113.318+2.209t\]

Kutumia teknolojia, mgawo wa uwiano ulihesabiwa kuwa 0.9965, unaonyesha mwenendo mkubwa wa kuongezeka kwa mstari.

Kutumia hii kutabiri matumizi ya mwaka\((t=14)\) 2008,

\[\begin{align} C(14)&=113.318+2.209(14) \\ &=144.244 \end{align}\]

Mfano huo unatabiri galoni bilioni 144.244 za matumizi ya petroli mwaka 2008.

Zoezi\(\PageIndex{1}\)

Kutumia mfano sisi umba kwa kutumia teknolojia katika Mfano\(\PageIndex{6}\) kutabiri matumizi ya gesi katika 2011. Je, hii ni tafsiri au extrapolation?

Jibu

150.871 bilioni galoni; extrapolation

Dhana muhimu

• Viwanja vya kuwatawanya vinaonyesha uhusiano kati ya seti mbili za data.
• Kuwatawanya viwanja inaweza kuwakilisha mifano ya mstari au isiyo ya mstari.
• Mstari wa fit bora inaweza kuhesabiwa au kuhesabiwa, kwa kutumia calculator au programu ya takwimu.
• Ufuatiliaji unaweza kutumika kutabiri maadili ndani ya uwanja na aina mbalimbali za data, wakati extrapolation inaweza kutumika kutabiri maadili nje ya uwanja na aina mbalimbali ya data.
• Mgawo wa uwiano\(r\),, inaonyesha kiwango cha uhusiano wa mstari kati ya data.
• Mstari wa kurudi nyuma unafaa data.
• Mstari mdogo wa kurudi nyuma hupatikana kwa kupunguza mraba wa umbali wa pointi kutoka kwenye mstari unaopita kupitia data na inaweza kutumika kufanya utabiri kuhusu mojawapo ya vigezo.