2.3: Mfano na Kazi za Mstari

Last updated
Save as PDF

Page ID: 181421

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Jenga mifano ya mstari kutoka kwa maelezo ya maneno.
Tengeneza seti ya data na kazi ya mstari.

Emily ni mwanafunzi wa chuo ambaye ana mpango wa kutumia majira ya joto katika Seattle. Amehifadhi $3,500 kwa safari yake na anatarajia kutumia $400 kila wiki kwa kodi, chakula, na shughuli. Tunawezaje kuandika mfano wa mstari ili kuwakilisha hali yake? Je, itakuwa x-intercept, na anaweza kujifunza nini kutoka kwao? Ili kujibu maswali haya na kuhusiana, tunaweza kuunda mfano kwa kutumia kazi ya mstari. Mifano kama hii inaweza kuwa muhimu sana kwa kuchambua mahusiano na kufanya utabiri kulingana na mahusiano hayo. Katika sehemu hii, sisi kuchunguza mifano ya mifano ya kazi linear.

alt — Kielelezo$\PageIndex{1}$: (mikopo: EK Photography/Flickr)

Kutambua Hatua za Mfano na Kutatua Matatizo

Wakati modeling matukio na kazi linear na kutatua matatizo yanayohusisha kiasi na kiwango cha mara kwa mara ya mabadiliko, sisi kawaida kufuata mikakati hiyo tatizo kwamba tunataka kutumia kwa aina yoyote ya kazi. Hebu tuchunguze kwa ufupi:

Tambua kubadilisha kiasi, na kisha ufafanue vigezo vya maelezo ili kuwakilisha kiasi hicho. Ikiwa inafaa, mchoro picha au ufafanue mfumo wa kuratibu.
Soma kwa makini tatizo ili kutambua habari muhimu. Angalia habari ambayo hutoa maadili kwa vigezo au maadili kwa sehemu za mfano wa kazi, kama vile mteremko na thamani ya awali.
Soma kwa makini tatizo ili kujua kile tunachojaribu kupata, kutambua, kutatua, au kutafsiri.
Tambua njia ya suluhisho kutoka kwa taarifa iliyotolewa kwa kile tunachojaribu kupata. Mara nyingi hii itahusisha kuangalia na kufuatilia vitengo, kujenga meza, au hata kutafuta fomu ya kazi inayotumiwa kutengeneza tatizo.
Ikiwa inahitajika, weka formula ya kazi.
Tatua au tathmini kazi kwa kutumia formula.
Fikiria kama jibu lako ni busara kwa hali fulani na kama ni mantiki hesabu.
Fanya wazi matokeo yako kwa kutumia vitengo vinavyofaa, na jibu kwa sentensi kamili wakati wa lazima.

Kujenga Mifano ya mstari

Sasa hebu tuangalie mwanafunzi huko Seattle. Katika hali yake, kuna kiasi kikubwa cha kubadilisha: muda na pesa. Kiasi cha fedha alichobaki wakati wa likizo inategemea muda gani anakaa. Tunaweza kutumia habari hii kufafanua vigezo vyetu, ikiwa ni pamoja na vitengo.

Pato:$M$, fedha iliyobaki, kwa dola
Ingiza:$t$, wakati, katika wiki

Hivyo, kiasi cha fedha kilichobaki kinategemea idadi ya wiki:$M(t)$

Tunaweza pia kutambua thamani ya awali na kiwango cha mabadiliko.

Thamani ya awali: Aliokoa $3,500, hivyo $3,500 ni thamani ya awali ya M.
Kiwango cha Mabadiliko: Anatarajia kutumia $400 kila wiki, hivyo - $400 kwa wiki ni kiwango cha mabadiliko, au mteremko.

Kumbuka kwamba kitengo cha dola kwa wiki mechi kitengo cha variable yetu pato kugawanywa na variable yetu pembejeo. Pia, kwa sababu mteremko ni hasi, kazi ya mstari inapungua. Hii inapaswa kuwa na maana kwa sababu anatumia pesa kila wiki.

Kiwango cha mabadiliko ni mara kwa mara, hivyo tunaweza kuanza na mfano wa mstari$M(t)=mt+b$. Kisha tunaweza kubadilisha uingizaji na mteremko uliotolewa.

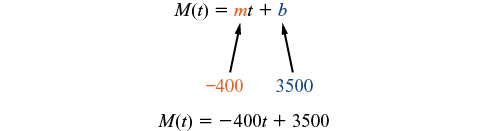
Ili kupata x-intercept, tunaweka pato kwa sifuri, na tatua kwa pembejeo.

\[\begin{align*} 0&=−400t+3500 \\ t&=\dfrac{3500}{400} \\ &=8.75 \end{align*}\]

X-intercept ni wiki 8.75. Kwa sababu hii inawakilisha thamani ya pembejeo wakati pato itakuwa sifuri, tunaweza kusema kwamba Emily hatakuwa na pesa iliyoachwa baada ya wiki 8.75.

Wakati wa kuimarisha hali yoyote ya maisha halisi na kazi, kuna kawaida uwanja mdogo juu ya ambayo mfano huo utakuwa halali-karibu hakuna mwenendo unaoendelea kwa muda usiojulikana. Hapa uwanja unahusu idadi ya wiki. Katika kesi hii, haina mantiki kwa majadiliano juu ya maadili pembejeo chini ya sifuri. Thamani ya pembejeo hasi inaweza kutaja wiki kadhaa kabla ya kuokolewa $3,500, lakini hali iliyojadiliwa inaleta swali mara moja alipohifadhi $3,500 kwa sababu hii ni wakati safari yake na matumizi ya baadaye huanza. Pia kuna uwezekano kwamba mtindo huu si halali baada ya x-intercept, isipokuwa Emily itatumia kadi ya mkopo na huenda katika madeni. Domain inawakilisha seti ya maadili ya pembejeo, hivyo uwanja busara kwa ajili ya kazi hii ni$0{\leq}t{\leq}8.75$.

Katika mfano hapo juu, tulipewa maelezo yaliyoandikwa ya hali hiyo. Tulifuata hatua za kuimarisha tatizo kuchambua habari. Hata hivyo, taarifa zinazotolewa haziwezi kuwa sawa. Wakati mwingine tunaweza kuwa zinazotolewa na intercept. Wakati mwingine tunaweza kutolewa na thamani ya pato. Lazima tuwe makini kuchambua habari tunayopewa, na kuitumia ipasavyo ili kujenga mfano wa mstari.

Kutumia Kupinga Kupewa Kujenga Mfano

Baadhi ya matatizo halisi ya ulimwengu hutoa y-intercept, ambayo ni thamani ya mara kwa mara au ya awali. Mara baada ya y-intercept inajulikana, x-intercept inaweza kuhesabiwa. Tuseme, kwa mfano, kwamba Hana ana mpango wa kulipa mkopo usio na riba kutoka kwa wazazi wake. Mizani yake ya mkopo ni $1,000. Anapanga kulipa $250 kwa mwezi mpaka usawa wake ni $0. Y-intercept ni kiasi cha awali cha deni lake, au $1,000. Kiwango cha mabadiliko, au mteremko, ni $250 kwa mwezi. Tunaweza kutumia fomu ya kuingilia mteremko na taarifa iliyotolewa ili kuendeleza mfano wa mstari.

\[\begin{align*} f(x)&=mx+b \\ &=-250x+1000 \end{align*}\]

Sasa tunaweza kuweka kazi sawa na 0, na kutatua kwa$x$ kupata x-intercept.

\[\begin{align*} 0&=-250+1000 \\ 1000&=250x \\ 4&=x \\ x&=4 \end{align*}\]

X-intercept ni idadi ya miezi inachukua yake kufikia usawa wa $0. X-intercept ni miezi minne, hivyo itachukua Hannah miezi minne kulipa mkopo wake.

Kutumia Pembejeo na Pato la Kujenga Mfano

Wengi maombi halisi ya dunia si kama moja kwa moja kama wale sisi tu kuchukuliwa. Badala yake zinahitaji sisi kutambua baadhi ya nyanja ya kazi linear. Tunaweza wakati mwingine badala kuulizwa kutathmini mfano linear katika pembejeo fulani au kuweka equation ya mfano linear sawa na pato maalum.

$alt$ Kutokana na tatizo la neno linalojumuisha jozi mbili za maadili ya pembejeo na pato, tumia kazi ya mstari ili kutatua tatizo.

Tambua maadili ya pembejeo na pato.
Badilisha data kwa jozi mbili za kuratibu.
Pata mteremko.
Andika mfano wa mstari.
Tumia mfano wa kufanya utabiri kwa kutathmini kazi kwa thamani ya x-iliyopewa.
Tumia mfano kutambua thamani ya x ambayo husababisha thamani ya y iliyotolewa.
Jibu swali lililofanywa.

Mfano$\PageIndex{1}$: Using a Linear Model to Investigate a Town’s Population

Idadi ya wakazi wa mji imekuwa ikiongezeka kwa mstari. Mwaka 2004 idadi ya wakazi ilikuwa 6,200. Kufikia 2009 idadi ya watu ilikuwa imeongezeka hadi 8,100. Kudhani hali hii inaendelea.

Kutabiri idadi ya watu katika 2013.
Tambua mwaka ambao idadi ya watu itafikia 15,000.

Suluhisho

Kiasi cha kubadilisha mbili ni ukubwa wa idadi ya watu na wakati. Wakati tunaweza kutumia thamani halisi ya mwaka kama wingi pembejeo, kufanya hivyo huelekea kusababisha milinganyo mbaya sana kwa sababu y-intercept ingekuwa yanahusiana na mwaka 0, zaidi ya miaka 2000 iliyopita!

Kufanya hesabu nicer kidogo, tutafafanua pembejeo yetu kama idadi ya miaka tangu 2004:

Ingiza:$t$, miaka tangu 2004
Pato:$P(t)$, idadi ya wakazi wa mji

Kutabiri idadi ya watu katika 2013 ($t=9$), tunataka kwanza haja equation kwa idadi ya watu. Vivyo hivyo, ili kupata wakati idadi ya watu itafikia 15,000, tunahitaji kutatua kwa pembejeo ambayo itatoa pato la 15,000. Kuandika equation, tunahitaji thamani ya awali na kiwango cha mabadiliko, au mteremko.

Kuamua kiwango cha mabadiliko, tutatumia mabadiliko katika pato kwa mabadiliko katika pembejeo.

\[m=\dfrac{\text{change in output}}{\text{change in input}}\]

Tatizo linatupa jozi mbili za pembejeo-pato. Kuwabadilisha ili kufanana na vigezo vyetu vilivyofafanuliwa, mwaka 2004 ungekuwa yanahusiana na$t=0$, kutoa uhakika$(0,6200)$. Kumbuka kwamba kwa njia ya uchaguzi wetu wajanja wa ufafanuzi wa kutofautiana, tumejipatia “sisi wenyewe” y-intercept ya kazi. mwaka 2009 ingekuwa yanahusiana na$t=5$, kutoa uhakika$(5,8100)$.

jozi mbili kuratibu ni$(0,6200)$ na$(5,8100)$. Kumbuka kwamba tulikutana na mifano ambayo tulipewa pointi mbili mapema katika sura. Tunaweza kutumia maadili haya kuhesabu mteremko.

\[\begin{align*} m&=\dfrac{8100-6200}{5-0}\\ &=\dfrac{1900}{5} \\ &=380 \text{ people per year} \end{align*}\]

Tayari tunajua y-intercept ya mstari, hivyo tunaweza kuandika mara moja equation:

\[P(t)=380t+6200\]

Kutabiri idadi ya watu katika 2013, sisi kutathmini kazi yetu katika$t=9$.

\[\begin{align*} P(9)&=380(9)+6,200 \\ &=9,620 \end{align*}\]

Ikiwa mwenendo unaendelea, mfano wetu unatabiri idadi ya 9,620 mwaka 2013.

Ili kupata wakati idadi ya watu itafikia 15,000, tunaweza kuweka$P(t)=15000$ na kutatua$t$.

\[\begin{align*} 15000&=380t+6200 \\ 8800&=380t \\ t&{\approx}23.158 \end{align*}\]

Mfano wetu unatabiri idadi ya watu kufikia 15,000 katika kidogo zaidi ya miaka 23 baada ya 2004, au mahali fulani karibu na mwaka 2027.

Zoezi$\PageIndex{1A}$

Kampuni inauza donuts. Wanapata gharama ya kudumu ya $25,000 kwa kodi, bima, na gharama nyingine. Inachukua $0.25 ili kuzalisha kila donut.

Andika mfano linear kuwakilisha gharama C ya kampuni kama kazi ya$x$, idadi ya donuts zinazozalishwa.
Pata na kutafsiri y-intercept.

Suluhisho

a.$C(x)=0.25x+25,000$ b. y-intercept ni$(0,25,000)$. Ikiwa kampuni haina kuzalisha donut moja, bado inakabiliwa na gharama ya $25,000.

Zoezi$\PageIndex{1B}$

Idadi ya wakazi wa mji imekuwa ikiongezeka kwa mstari. Mwaka 2008, idadi ya wakazi ilikuwa 28,200. Kufikia mwaka 2012, idadi ya wakazi ilikuwa 36,800. Kudhani hali hii inaendelea.

Kutabiri idadi ya watu katika 2014.
Tambua mwaka ambao idadi ya watu itafikia 54,000.

Suluhisho

a. 41,100 b. 2020

Kutumia Mchoro wa Mfano wa Tatizo

Ni muhimu kwa maombi mengi ya ulimwengu halisi kuteka picha ili kupata hisia ya jinsi vigezo vinavyowakilisha pembejeo na pato vinaweza kutumika kujibu swali. Ili kuteka picha, kwanza fikiria nini tatizo linaomba. Kisha, tambua pembejeo na pato. Mchoro unapaswa kuhusisha vigezo. Mara nyingi, maumbo ya kijiometri au takwimu hutolewa. Umbali mara nyingi hufuatiliwa nje. Ikiwa pembetatu ya kulia imewekwa, Theorem ya Pythagorean inahusiana na pande. Kama mstatili ni sketched, lebo upana na urefu ni muhimu.

Mfano$\PageIndex{2}$: Using a Diagram to Model Distance Walked

Anna na Emanuel kuanza katika makutano sawa. Anna anatembea mashariki kwa maili 4 kwa saa wakati Emanuel anatembea kusini kwa maili 3 kwa saa. Wanawasiliana na redio ya njia mbili ambayo ina maili 2. Muda gani baada ya kuanza kutembea wataanguka nje ya mawasiliano ya redio?

Suluhisho

Kwa asili, tunaweza kujibu swali hili kwa kusema wataanguka nje ya mawasiliano ya redio wakati wao ni maili 2 mbali, ambayo inatuongoza kuuliza swali jipya:

“Itachukua muda gani kuwa umbali wa maili 2?”

Katika tatizo hili, kiasi chetu cha kubadilisha ni wakati na msimamo, lakini hatimaye tunahitaji kujua itachukua muda gani kwao kuwa umbali wa maili 2. Tunaweza kuona kwamba wakati itakuwa pembejeo yetu variable, hivyo tutaweza kufafanua pembejeo yetu na vigezo pato.

Ingiza:$t$, wakati kwa masaa.
Pato:$A(t)$, umbali katika maili, na$E(t)$, umbali katika maili

Kwa sababu ni dhahiri jinsi ya kufafanua pato yetu variable, tutaweza kuanza kwa kuchora picha kama vile Kielelezo$\PageIndex{3}$.

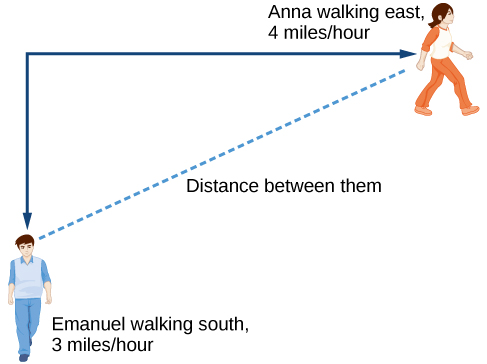
Thamani ya awali: Wote wawili huanza kwenye makutano sawa hivyo wakati$t=0$, umbali uliosafiri na kila mtu lazima pia uwe 0. Hivyo thamani ya awali kwa kila mmoja ni 0.
Kiwango cha Mabadiliko: Anna anatembea maili 4 kwa saa na Emanuel anatembea maili 3 kwa saa, ambayo ni viwango vya mabadiliko. Mteremko kwa$A$ ni 4 na mteremko kwa$E$ ni 3.

Kutumia maadili hayo, tunaweza kuandika formula kwa umbali kila mtu ametembea.

\[A(t)=4t\]

\[E(t)=3t\]

Kwa tatizo hili, umbali kutoka mwanzo ni muhimu. Ili kutaja haya, tunaweza kufafanua mfumo wa kuratibu, kutambua “hatua ya mwanzo” kwenye makutano ambapo wote walianza. Kisha tunaweza kutumia variable$A$, ambayo sisi kuletwa hapo juu, kuwakilisha nafasi Anna, na kufafanua kuwa kipimo kutoka hatua ya mwanzo katika mwelekeo wa mashariki. Vivyo hivyo, unaweza kutumia variable$E$, kuwakilisha msimamo Emanuel, kipimo kutoka hatua ya mwanzo katika mwelekeo kusini. Kumbuka kuwa katika kufafanua mfumo wa kuratibu, tumeelezea hatua ya mwanzo ya kipimo na mwelekeo wa kipimo.

Tunaweza kisha kufafanua variable tatu$D$,, kuwa kipimo cha umbali kati ya Anna na Emanuel. Showing vigezo kwenye mchoro mara nyingi husaidia, kama tunaweza kuona kutoka Kielelezo$\PageIndex{4}$.

Kumbuka kwamba tunahitaji kujua muda gani inachukua$D$, umbali kati yao, sawa na maili 2. Kumbuka kwamba kwa pembejeo yoyote$t$, matokeo$A(t)$,$E(t)$, na$D(t)$ kuwakilisha umbali.

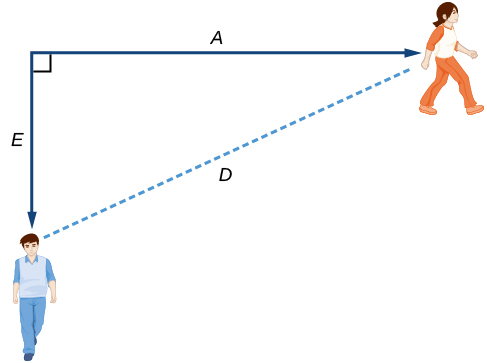
Tunaweza kutumia Theorem ya Pythagorean kwa sababu tumejenga angle sahihi. — Kielelezo$\PageIndex{4}$: Tunaweza kutumia Theorem ya Pythagorean kwa sababu tumepata pembe sahihi.

Kutumia Theorem ya Pythagorean, tunapata:

\[\begin{align*} d(t)^2&=A(t)^2+E(t)^2 \\ &=(4t)^2+(3t)^2 \\ &=16t^2+9t^2 \\ &=25t^2 \\ D(t)&=\pm\sqrt{25t^2} &\text{Solve for $D(t)$ using the square root} \\ &= \pm 5|t| \end{align*}\]

Katika hali hii sisi ni kuzingatia tu maadili chanya ya$t$, hivyo umbali wetu daima$D(t)$ kuwa chanya. Tunaweza kurahisisha jibu hili kwa$D(t)=5t$. Hii ina maana kwamba umbali kati ya Anna na Emanuel pia ni kazi ya mstari. Kwa sababu D ni kazi linear, sasa tunaweza kujibu swali la wakati umbali kati yao kufikia maili 2. Tutaweka pato$D(t)=2$ na kutatua$t$.

\[\begin{align*} D(t)&=2 \\ 5t&=2 \\ t&=\dfrac{2}{5}=0.4 \end{align*}\]

Wataanguka nje ya mawasiliano ya redio katika masaa 0.4, au dakika 24.

$alt$ Lazima nipate kuteka michoro wakati unapopewa habari kulingana na sura ya kijiometri?

Ndiyo. Mchoro takwimu na uandike kiasi na haijulikani kwenye mchoro.

Mfano$\PageIndex{3}$: Using a Diagram to Model Distance between Cities

Kuna barabara moja kwa moja inayoongoza kutoka mji wa Westborough hadi Agritown 30 maili mashariki na 10 maili kaskazini. Partway chini ya barabara hii, ni makutano na barabara ya pili, perpendicular kwa kwanza, na kusababisha mji wa Eastborough. Kama mji wa Eastborough iko 20 maili moja kwa moja mashariki ya mji wa Westborough, jinsi mbali ni barabara makutano kutoka Westborough?

Suluhisho

Inaweza kusaidia hapa kuteka picha ya hali hiyo. Angalia Kielelezo$\PageIndex{5}$. Itakuwa kisha kuwa na manufaa kwa kuanzisha mfumo wa kuratibu. Wakati tunaweza kuweka asili mahali popote, kuiweka katika Westborough inaonekana rahisi. Hii unaweka Agritown katika kuratibu$(30, 10)$, na Eastborough katika$(20,0)$.

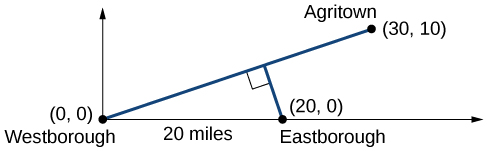
Kutumia hatua hii pamoja na asili, tunaweza kupata mteremko wa mstari kutoka Westborough hadi Agritown:

\[m=\dfrac{10-0}{30-0}=\dfrac{1}{3}\]

equation ya barabara kutoka Westborough kwa Agritown itakuwa

\[W(x)=\dfrac{1}{3}x\]

Kutokana na hili, tunaweza kuamua barabara perpendicular kwa Eastborough itakuwa na mteremko$m=–3$. Kwa sababu mji wa Eastborough ni katika hatua$(20, 0)$, tunaweza kupata equation:

\[\begin{align*} E(x)&=−3x+b \\ 0&=−3(20)+b &\text{Substitute in $(20, 0)$} \\ b&=60 \\ E(x)&=−3x+60 \end{align*}\]

Sasa tunaweza kupata kuratibu za makutano ya barabara kwa kutafuta makutano ya mistari hii. Kuwaweka sawa,

\[\begin{align*} \dfrac{1}{3}x&=−3x+60 \\ \dfrac{10}{3}x&=60 \\ 10x&=180 \\ x&=18 &\text{Substituting this back into $W(x)$} \\ y&=W(18) \\ &= \dfrac{1}{3}(18) \\&=6 \end{align*}\]

Barabara huingiliana wakati huo$(18,6)$. Kutumia formula ya umbali, sasa tunaweza kupata umbali kutoka Westborough hadi kwenye makutano.

\[\begin{align*} \text{distance}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\ &=\sqrt{(18-0)^2+(6-0)^2} \\ &\approx 18.743 \text{miles} \end{align*}\]

Uchambuzi

Matumizi moja mazuri ya mifano ya mstari ni kuchukua faida ya ukweli kwamba grafu za kazi hizi ni mistari. Hii inamaanisha programu halisi za ulimwengu zinazojadili ramani zinahitaji kazi za mstari ili kuiga umbali kati ya pointi za kumbukumbu.

Zoezi$\PageIndex{2}$

Kuna barabara moja kwa moja inayoongoza kutoka mji wa Timpson hadi Ashburn maili 60 mashariki na maili 12 kaskazini. Partway chini ya barabara, ni majadiliano na barabara ya pili, perpendicular kwa kwanza, na kusababisha mji wa Garrison. Kama mji wa Garrison iko 22 maili moja kwa moja mashariki ya mji wa Timpson, jinsi mbali ni barabara makutano kutoka Timpson?

Suluhisho

21.15 maili

Ujenzi wa Mifumo ya Mifano

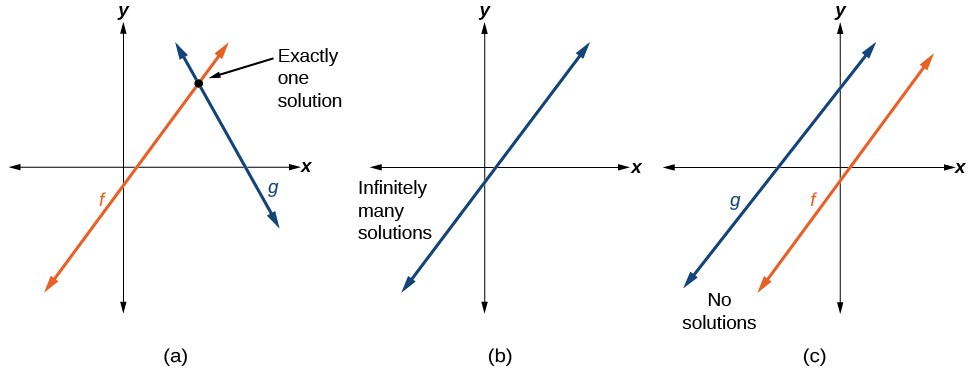
Hali halisi ya ulimwengu ikiwa ni pamoja na kazi mbili au zaidi linear inaweza kuwa inatokana na mfumo wa equations linear. Kumbuka, wakati wa kutatua mfumo wa equations linear, tunatafuta pointi mistari miwili inafanana. Kwa kawaida, kuna aina tatu za majibu iwezekanavyo, kama inavyoonekana katika Kielelezo$\PageIndex{6}$.

$alt$ Kutokana na hali ambayo inawakilisha mfumo wa equations linear, kuandika mfumo wa equations na kutambua suluhisho.

Tambua pembejeo na pato la kila mfano wa mstari.
Tambua mteremko na y-intercept ya kila mfano wa mstari.
Pata suluhisho kwa kuweka kazi mbili za mstari sawa na mwingine na kutatua$x$, au kupata hatua ya makutano kwenye grafu.

Mfano$\PageIndex{4}$: Building a System of Linear Models to Choose a Truck Rental Company

Jamal anachagua kati ya makampuni mawili ya kukodisha lori. kwanza, Kuendelea Trucking, Inc., mashtaka ada up-mbele ya $20, kisha 59 senti maili [1]. Ya pili, Move It Your Way, inadai ada ya juu ya mbele ya $16, halafu senti 63 kwa maili. Lini Kuendelea Trucking, Inc. kuwa chaguo bora kwa Jamal?

Suluhisho

Kiasi mbili muhimu katika tatizo hili ni gharama na idadi ya maili inayotokana. Kwa sababu tuna makampuni mawili ya kuzingatia, tutafafanua kazi mbili.

Ingiza:$d$, umbali unaendeshwa katika maili
Matokeo:$K(d):$ gharama, kwa dola, kwa ajili ya kukodisha kutoka Keep on Trucking

$M(d):$gharama, kwa dola, kwa ajili ya kukodisha kutoka Move It Njia yako

Thamani ya awali: Up-Front ada:$K(0)=20$ na$M(0)=16$
Kiwango cha Mabadiliko:$K(d)=\dfrac{$0.59}{\text{mile}}$ na$P(d)=\dfrac{$0.63}{\text{mile}}$

Kazi ya mstari ni ya fomu$f(x)=mx+b$. Kutumia viwango vya mabadiliko na mashtaka ya awali, tunaweza kuandika equations

\[K(d)=0.59d+20 \nonumber\]

\[M(d)=0.63d+16 \nonumber\]

Kutumia milinganyo haya, tunaweza kuamua wakati Endelea Trucking, Inc. itakuwa chaguo bora. Kwa sababu wote tuna kufanya uamuzi huo kutoka ni gharama, sisi ni kuangalia kwa wakati Keep on Trucking, Inc. gharama kidogo, au wakati$K(d)<M(d)$. Njia ya ufumbuzi itatuongoza kupata equations kwa kazi mbili, kupata makutano, na kisha kuona ambapo$K(d)$ kazi ni ndogo.

Grafu hizi ni sketched katika Kielelezo$\PageIndex{7}$, na$K(d)$ katika bluu.

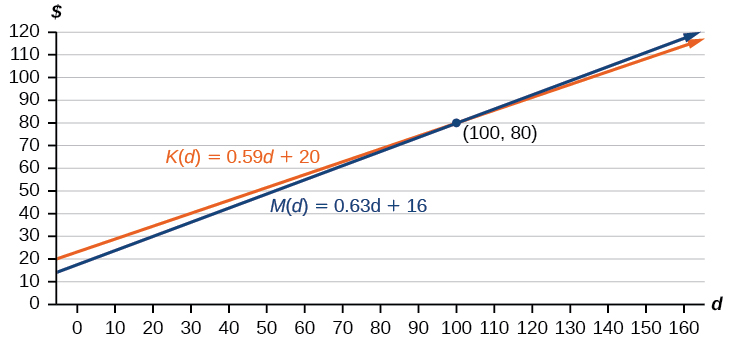
Ili kupata makutano, tunaweka equations sawa na kutatua:

\[\begin{align*} K(d)&=M(d) \\ 0.59d+20&=0.63d+16 \\ 4&=0.04d \\ 100&=d \\ d&=100 \end{align*}\]

Hii inatuambia kwamba gharama kutoka makampuni mawili itakuwa sawa kama 100 maili ni inaendeshwa. Aidha kwa kuangalia grafu, au akibainisha kuwa$K(d)$ inakua kwa kiwango cha polepole, tunaweza kuhitimisha kuwa Endelea Trucking, Inc. itakuwa bei nafuu wakati zaidi ya maili 100 zinaendeshwa, yaani$d>100$.

Dhana muhimu

Tunaweza kutumia mikakati hiyo tatizo kwamba tunataka kutumia kwa aina yoyote ya kazi.
Wakati wa kuimarisha na kutatua tatizo, tambua vigezo na uangalie maadili muhimu, ikiwa ni pamoja na mteremko na y-intercept.
Chora mchoro, ikiwa inafaa.
Angalia kwa busara ya jibu.
Mifano ya mstari inaweza kujengwa kwa kutambua au kuhesabu mteremko na kutumia y-intercept.
X-intercept inaweza kupatikana kwa kuweka$y=0$, ambayo ni kuweka maneno$mx+b$ sawa na 0.
Hatua ya makutano ya mfumo wa equations linear ni hatua ambapo x- na y maadili ni sawa.
Grafu ya mfumo inaweza kutumika kutambua pointi ambapo mstari mmoja unaanguka chini (au juu) mstari mwingine.

maelezo ya chini

Viwango vya 1 Rudishwa Agosti 2, 2010 kutoka www.budgettruck.com na http://www.uhaul.com/