2.2: Grafu ya Kazi za Mstari

Malengo ya kujifunza

• Graph kazi linear.
• Andika equation kwa kazi linear kutoka grafu ya mstari.
• Kutokana na usawa wa mistari miwili, onyesha kama grafu zao ni sambamba au perpendicular.
• Andika equation ya mstari sambamba au perpendicular kwa mstari fulani.
• Tatua mfumo wa equations linear.

Makampuni mawili ya simu ya mashindano hutoa mipango tofauti ya malipo. Mipango miwili hulipa kiwango sawa kwa dakika ya umbali mrefu, lakini malipo ya ada tofauti ya kila mwezi ya gorofa. Mtumiaji anataka kuamua kama mipango miwili itawahi gharama kiasi sawa kwa idadi fulani ya dakika za umbali mrefu kutumika. Gharama ya jumla ya kila mpango wa malipo inaweza kuwakilishwa na kazi ya mstari. Ili kutatua tatizo, tutahitaji kulinganisha kazi. Katika sehemu hii, tutazingatia njia za kulinganisha kazi kwa kutumia grafu.

Graphing Linear Kazi

Hapo awali, tuliona kwamba grafu ya kazi ya mstari ni mstari wa moja kwa moja. Tuliweza pia kuona pointi za kazi pamoja na thamani ya awali kutoka kwenye grafu. Kwa kuchora kazi mbili, basi, tunaweza kulinganisha sifa zao kwa urahisi zaidi. Kuna mbinu tatu za msingi za kuchora kazi za mstari:

1. Panda pointi na kisha kuchora mstari kupitia pointi.
2. Tumia y-intercept na mteremko.
3. Tumia mabadiliko ya kazi ya utambulisho$f(x)=x$.

Kuchora Kazi kwa Pointi za Kupanga

Ili kupata pointi za kazi, tunaweza kuchagua maadili ya pembejeo, tathmini kazi katika maadili haya ya pembejeo, na uhesabu maadili ya pato. Maadili ya pembejeo na maadili ya pato yanayofanana huunda jozi za kuratibu. Sisi kisha njama jozi kuratibu kwenye gridi ya taifa. Kwa ujumla, tunapaswa kutathmini kazi kwa kiwango cha chini cha pembejeo mbili ili kupata angalau pointi mbili kwenye grafu. Kwa mfano, kutokana na kazi,$f(x)=2x$, tunaweza kutumia maadili pembejeo 1 na 2. Kutathmini kazi kwa thamani ya pembejeo ya 1 hutoa thamani ya pato la 2, ambayo inawakilishwa na uhakika$(1,2)$. Kutathmini kazi kwa thamani ya pembejeo ya 2 hutoa thamani ya pato la 4, ambayo inawakilishwa na uhakika$(2,4)$. Kuchagua pointi tatu mara nyingi ni vyema kwa sababu kama pointi zote tatu hazianguka kwenye mstari huo, tunajua tumefanya kosa.

Jinsi ya: Kutokana na kazi ya mstari, grafu kwa pointi za kupanga.

1. Chagua kiwango cha chini cha maadili mawili ya pembejeo.
2. Tathmini kazi katika kila thamani ya pembejeo.
3. Tumia maadili ya pato ili kutambua jozi za kuratibu.
4. Panda jozi za kuratibu kwenye gridi ya taifa.
5. Chora mstari kupitia pointi.

Mfano$\PageIndex{1}$: Graphing by Plotting Points

Grafu$f(x)=−\frac{2}{3}x+5$ kwa pointi za kupanga njama.

Suluhisho

Anza kwa kuchagua maadili ya pembejeo. Kazi hii inajumuisha sehemu na denominator ya 3, basi hebu tuchague mizigo ya 3 kama maadili ya pembejeo. Tutachagua 0, 3, na 6.

Tathmini kazi kwa kila thamani ya pembejeo, na utumie thamani ya pato kutambua jozi za kuratibu.

$$\begin{align*} x&=0 & f(0)&=-\dfrac{2}{3}(0)+5=5\rightarrow(0,5) \\ x&=3 & f(3)&=-\dfrac{2}{3}(3)+5=3\rightarrow(3,3) \\ x&=6 & f(6)&=-\dfrac{2}{3}(6)+5=1\rightarrow(6,1) \end{align*}$$

Panda jozi za kuratibu na kuteka mstari kupitia pointi. Kielelezo$\PageIndex{1}$ kinawakilisha grafu ya kazi$f(x)=−\frac{2}{3}x+5$.

Kielelezo$\PageIndex{1}$: Grafu ya kazi ya mstari$f(x)=−\frac{2}{3}x+5$.

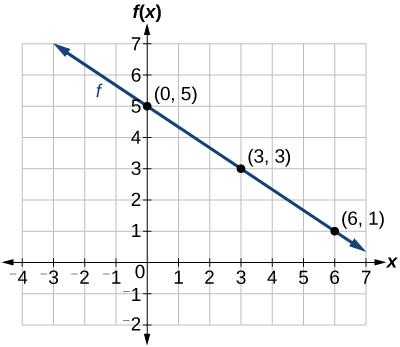
Uchambuzi

Grafu ya kazi ni mstari kama inavyotarajiwa kwa kazi ya mstari. Kwa kuongeza, grafu ina slant chini, ambayo inaonyesha mteremko hasi. Hii pia inatarajiwa kutoka kiwango hasi mara kwa mara ya mabadiliko katika equation kwa ajili ya kazi.

Zoezi$\PageIndex{1}$

Grafu$f(x)=−\frac{3}{4}x+6$ kwa pointi za kupanga njama.

Jibu

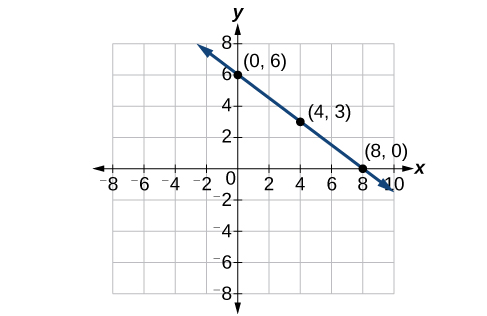
Kielelezo$\PageIndex{2}$

Graphing Kazi Kutumia y-intercept na Slope

Njia nyingine ya kuchora kazi za mstari ni kwa kutumia sifa maalum za kazi badala ya kupanga njama. Tabia ya kwanza ni y-intercept yake, ambayo ni hatua ambayo thamani ya pembejeo ni sifuri. Ili kupata y-intercept, tunaweza kuweka$x=0$ katika equation.

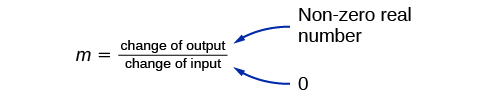
Tabia nyingine ya kazi ya mstari ni mteremko wake$m$, ambayo ni kipimo cha mwinuko wake. Kumbuka kwamba mteremko ni kiwango cha mabadiliko ya kazi. Mteremko wa kazi ni sawa na uwiano wa mabadiliko katika matokeo kwa mabadiliko katika pembejeo. Njia nyingine ya kufikiri juu ya mteremko ni kwa kugawanya tofauti ya wima, au kupanda, kwa tofauti ya usawa, au kukimbia. Tulikutana na y-intercept na mteremko katika Kazi za Linear.

Hebu fikiria kazi ifuatayo.

$$f(x)=\dfrac{1}{2}x+1$$

Mteremko ni$\frac{1}{2}$. Kwa sababu mteremko ni chanya, tunajua grafu itapanda juu kutoka kushoto kwenda kulia. Y-intercept ni hatua kwenye grafu wakati$x=0$. Grafu huvuka mhimili wa y$(0,1)$. Sasa tunajua mteremko na y-intercept. Tunaweza kuanza graphing kwa kupanga njama$(0,1)$ Tunajua kwamba mteremko ni kupanda juu ya kukimbia,$m=\frac{\text{rise}}{\text{run}}$. Kutoka kwa mfano wetu, tuna$m=\frac{1}{2}$, ambayo ina maana kwamba kupanda ni 1 na kukimbia ni 2. Hivyo kuanzia yetu y-intercept$(0,1)$, tunaweza kupanda 1 na kisha kukimbia 2, au kukimbia 2 na kisha kupanda 1. Tunarudia mpaka tuna pointi chache, na kisha tunapata mstari kupitia pointi kama inavyoonekana kwenye Kielelezo$\PageIndex{3}$.

Kielelezo$\PageIndex{3}$: Grafu ya$f(x)$ kuonyesha mteremko na y-intercept

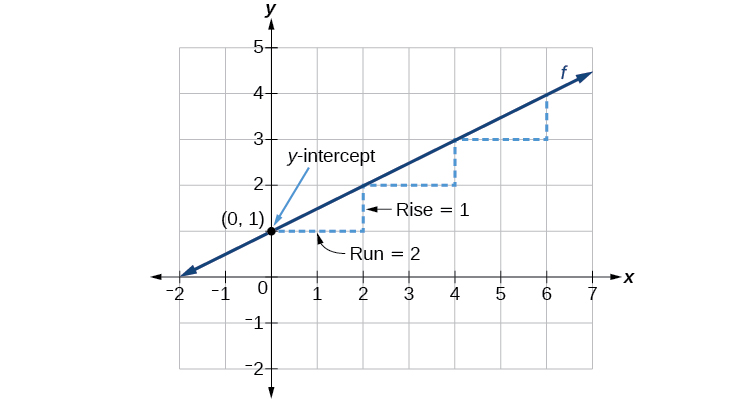
Ufafanuzi wa picha ya Kazi ya Linear

Katika equation$f(x)=mx+b$

• $b$ni y-intercept ya grafu na inaonyesha$(0,b)$ hatua ambayo grafu huvuka mhimili wa y.
• $m$ni mteremko wa mstari na inaonyesha uhamisho wa wima (kupanda) na uhamisho wa usawa (kukimbia) kati ya kila jozi mfululizo wa pointi. Kumbuka formula ya mteremko:

$$m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}$$

Zoezi$\PageIndex{1}$

Je! Kazi zote za mstari zina y-intercepts?

Jibu

Ndiyo. Kazi zote za mstari zinavuka mhimili wa y na kwa hiyo zina y-intercepts. (Kumbuka: Mstari wa wima unaofanana na mhimili wa y hauna y-intercept, lakini sio kazi.)

Jinsi ya: Kutokana na equation kwa kazi linear, grafu kazi kwa kutumia y-intercept na mteremko.

1. Tathmini kazi kwa thamani ya pembejeo ya sifuri ili kupata y-intercept.
2. Tambua mteremko kama kiwango cha mabadiliko ya thamani ya pembejeo.
3. Panda hatua iliyowakilishwa na y-intercept.
4. Tumia$\frac{\text{rise}}{\text{run}}$ kuamua angalau pointi mbili zaidi kwenye mstari.
5. Mchoro mstari unaopita kupitia pointi.

Mfano$\PageIndex{2}$: Graphing by Using the y-intercept and Slope

Grafu$f(x)=−\frac{2}{3}x+5$ kutumia y-intercept na mteremko.

Suluhisho

Tathmini kazi katika$x=0$ kupata y-intercept. Thamani ya pato wakati$x=0$ ni 5, hivyo grafu itavuka mhimili wa y$(0,5)$.

Kwa mujibu wa equation kwa kazi, mteremko wa mstari ni$-\frac{2}{3}$. Hii inatuambia kwamba kwa kila kupungua kwa wima katika “kupanda” kwa vitengo -2, “kukimbia” huongezeka kwa vitengo 3 katika mwelekeo usawa. Sasa tunaweza graph kazi kwa kwanza kupanga y-intercept kwenye grafu katika Kielelezo$\PageIndex{4}$. Kutoka thamani ya awali$(0,5)$ tunahamia vitengo 2 na vitengo 3 vya haki. Tunaweza kupanua mstari upande wa kushoto na kulia kwa kurudia, na kisha kuteka mstari kupitia pointi.

Kielelezo$\PageIndex{4}$: Grafu ya$f(x)$

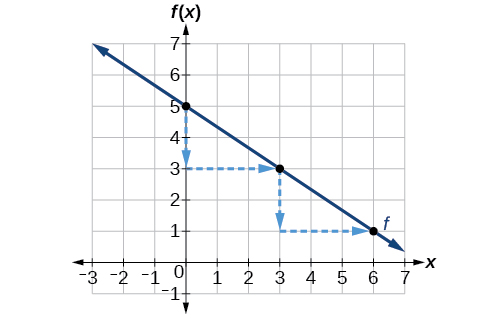
Uchambuzi

Grafu hupanda chini kutoka kushoto kwenda kulia, ambayo inamaanisha ina mteremko hasi kama inavyotarajiwa.

Zoezi$\PageIndex{2}$

Pata uhakika kwenye grafu tuliyovuta Mfano$\PageIndex{2}$ ambao una thamani ya x-hasi.

Jibu

Majibu iwezekanavyo ni pamoja na$(−3,7)$$(−6,9)$,, au$(−9,11)$.

Graphing Kazi Kutumia Mabadiliko

Chaguo jingine la kuchora ni kutumia mabadiliko ya kazi ya utambulisho$f(x)=x$. kazi inaweza kubadilishwa kwa kuhama juu, chini, kushoto, au kulia. Kazi inaweza pia kubadilishwa kwa kutumia kutafakari, kunyoosha, au compression.

Kuweka wima au Ukandamizaji

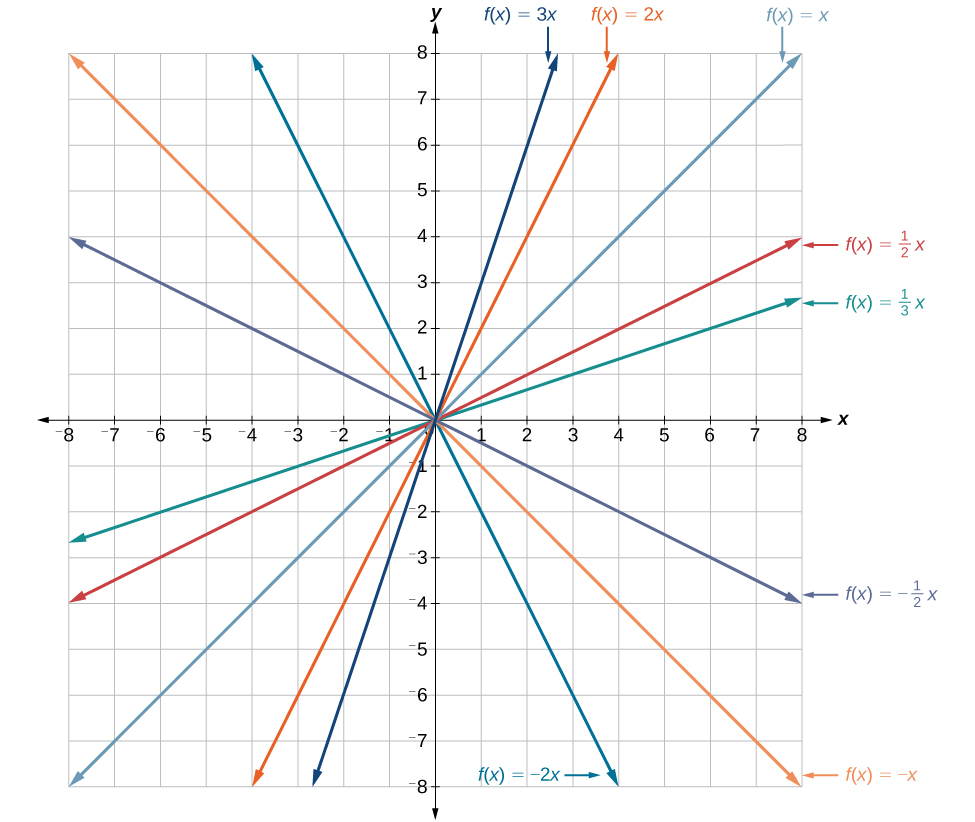
Katika equation$f(x)=mx$,$m$ ni kaimu kama kunyoosha wima au compression ya kazi utambulisho. Wakati$m$ ni hasi, pia kuna kutafakari wima ya grafu. Taarifa katika Kielelezo$\PageIndex{5}$ kwamba kuzidisha equation ya$f(x)=x$ na$m$ stretches grafu ya$f$ kwa sababu ya$m$ vitengo kama$m>1$ na compresses graph ya$f$ kwa sababu ya$m$ vitengo kama$0<m<1$. Hii ina maana kubwa thamani kamili ya$m$, steeper mteremko.

Kielelezo$\PageIndex{5}$: Kuweka wima na compressions na kutafakari juu ya kazi$f(x)=x$.

Shift ya wima

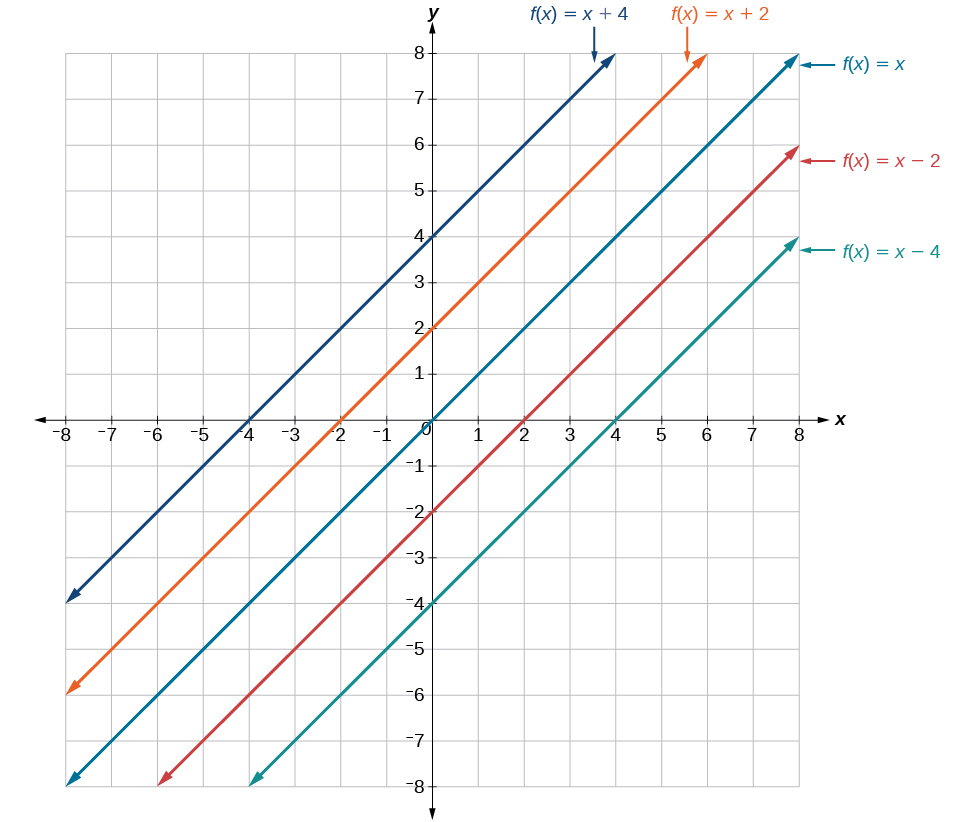
Katika$f(x)=mx+b$,$b$ vitendo kama mabadiliko ya wima, kusonga grafu juu na chini bila kuathiri mteremko wa mstari. Taarifa katika Kielelezo$\PageIndex{6}$ kwamba kuongeza thamani ya$b$ equation ya$f(x)=x$ mabadiliko grafu ya jumla$f$ ya$b$ vitengo up kama$b$ ni chanya na$|b|$ vitengo chini kama$b$ ni hasi.

Kielelezo$\PageIndex{6}$: Grafu hii inaonyesha mabadiliko ya wima ya kazi$f(x)=x$.

Kutumia kunyoosha wima au compressions pamoja na mabadiliko ya wima ni njia nyingine ya kuangalia kutambua aina tofauti za kazi za mstari. Ingawa hii inaweza kuwa njia rahisi ya kuchora aina hii ya kazi, bado ni muhimu kufanya kila njia.

Kutokana na usawa wa kazi ya mstari, tumia mabadiliko ya kuchora kazi ya mstari katika fomu$f(x)=mx+b$.

1. Grafu$f(x)=x$.
2. Kuweka kwa wima au compress grafu kwa sababu$m$.
3. Shift grafu juu au chini$b$ vitengo.

Mfano$\PageIndex{3}$​​​​​​​: Graphing by Using Transformations

Grafu$f(x)=\frac{1}{2}x−3$ kutumia mabadiliko.

Suluhisho

equation kwa ajili ya kazi inaonyesha kwamba$m=\frac{1}{2}$ hivyo kazi utambulisho ni wima USITUMIE na$\frac{1}{2}$. Equation kwa kazi pia inaonyesha kwamba$b=−3$ hivyo kazi ya utambulisho ni wima kubadilishwa chini vitengo 3. Kwanza, graph utambulisho kazi, na kuonyesha compression wima kama katika Kielelezo$\PageIndex{7}$.

Kielelezo$\PageIndex{7}$: kazi$y=x$, USITUMIE na sababu ya$\frac{1}{2}$.

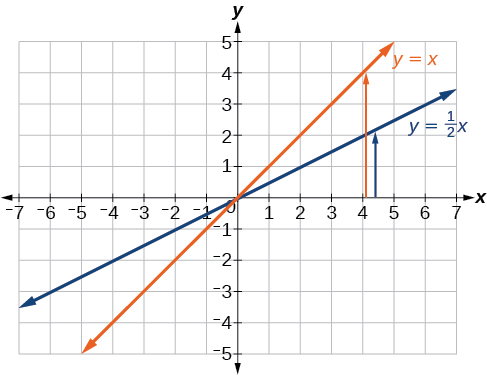
Kisha onyesha mabadiliko ya wima kama kwenye Kielelezo$\PageIndex{8}$.

Kielelezo$\PageIndex{8}$: Kazi$y=\frac{1}{2}x$, imebadilishwa chini vitengo 3.

Zoezi$\PageIndex{3}$

Grafu$f(x)=4+2x$, kwa kutumia mabadiliko.

Jibu

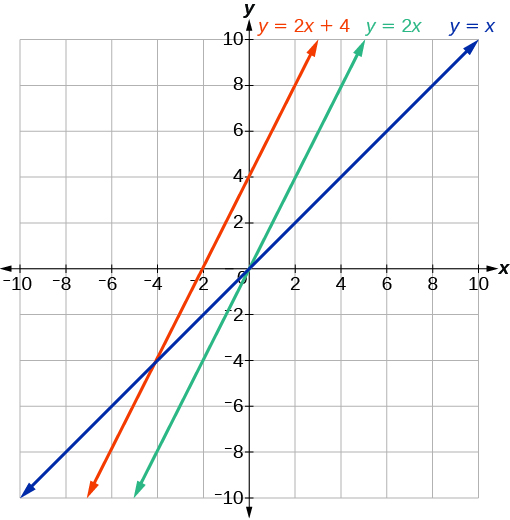
Kielelezo$\PageIndex{9}$

Katika Mfano 2.2.3, tungeweza kuchora grafu kwa kugeuza utaratibu wa mabadiliko?

Hapana. Utaratibu wa mabadiliko hufuata utaratibu wa shughuli. Wakati kazi inapimwa kwa pembejeo iliyotolewa, pato linalofanana linahesabiwa kwa kufuata utaratibu wa shughuli. Hii ndiyo sababu tulifanya compression kwanza. Kwa mfano, kufuata utaratibu: Hebu pembejeo iwe 2.

$$\begin{align} f(2)&=\dfrac{1}{2}(2)-3 \\ &=1-3\\ &=-2 \end{align}$$

Kuandika Equation kwa Kazi kutoka Grafu ya Line

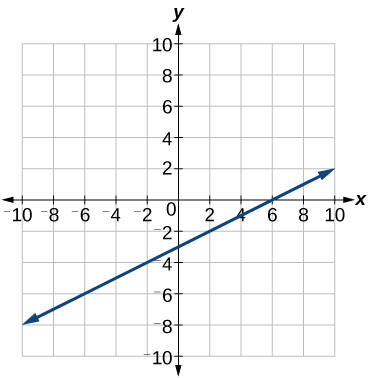
Kumbuka kwamba katika Kazi za Linear, tuliandika equation kwa kazi ya mstari kutoka kwenye grafu. Sasa tunaweza kupanua nini tunajua kuhusu graphing kazi linear kuchambua grafu kidogo kwa karibu zaidi. Anza kwa kuangalia Kielelezo$\PageIndex{10}$. Tunaweza kuona mara moja kwamba graph misalaba y mhimili katika hatua$(0, 4)$ hivyo hii ni y-intercept.

Kielelezo$\PageIndex{10}$: Grafu ya kazi ya mstari

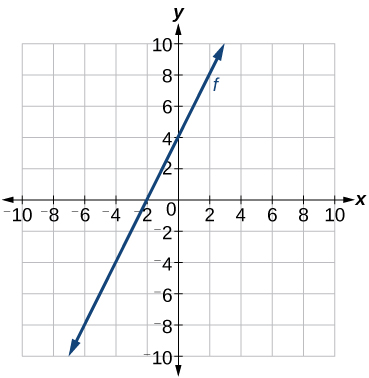
Kisha tunaweza kuhesabu mteremko kwa kutafuta kupanda na kukimbia. Tunaweza kuchagua pointi zozote mbili, lakini hebu tuangalie hatua (-2,0). Ili kupata kutoka hatua hii hadi y-intercept, tunapaswa kuhamisha vitengo 4 (kupanda) na vitengo 2 vya kulia (kukimbia). Hivyo mteremko lazima

$$m=\dfrac{\text{rise}}{\text{run}}=\dfrac{4}{2}=2$$

Kubadilisha mteremko na y-intercept katika fomu ya mteremko wa mstari hutoa

$$y=2x+4$$

Kutokana na grafu ya kazi linear, kupata equation kuelezea kazi.

1. Tambua y-intercept ya equation.
2. Chagua pointi mbili ili kuamua mteremko.
3. Kuweka y-intercept na mteremko ndani ya fomu ya mteremko wa mstari.

Mfano$\PageIndex{4}$​​​​​​​: Matching Linear Functions to Their Graphs

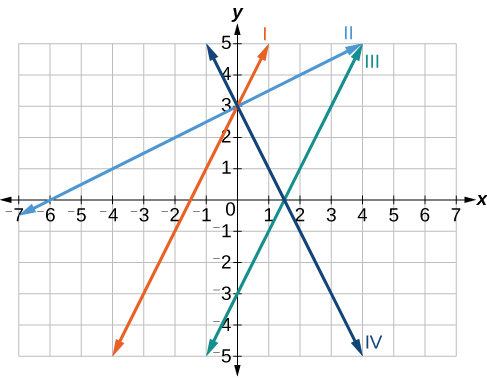
Mechi ya kila equation ya kazi linear na moja ya mistari katika Kielelezo$\PageIndex{11}$.

1. $f(x)=2x+3$
2. $g(x)=2x−3$
3. $h(x)=−2x+3$
4. $j(x)=\frac{1}{2}x+3$

Kielelezo$\PageIndex{11}$: Grafu ya kazi nne za mstari

Suluhisho

Kuchambua habari kwa kila kazi.

1. Kazi hii ina mteremko wa 2 na y-intercept ya 3. Inapaswa kupitisha hatua$(0, 3)$ na kupanda juu kutoka kushoto kwenda kulia. Tunaweza kutumia pointi mbili ili kupata mteremko, au tunaweza kulinganisha na kazi nyingine zilizoorodheshwa. Kazi$g$ ina mteremko huo, lakini tofauti ya y-intercept. Mistari ya I na III ina slant ileile kwa sababu wana mteremko uleule. Line III haina kupita katika$(0, 3)$ hivyo$f$ lazima kuwakilishwa na mstari I.
2. Kazi hii pia ina mteremko wa 2, lakini y-intercept ya -3. Inapaswa kupitisha hatua$(0,−3)$ na kupanda juu kutoka kushoto kwenda kulia. Inapaswa kuwakilishwa na mstari wa III.
3. Kazi hii ina mteremko wa —2 na y-intercept ya 3. Hii ni kazi tu iliyoorodheshwa na mteremko hasi, hivyo ni lazima iwakilishwe na mstari wa IV kwa sababu hupanda chini kutoka kushoto kwenda kulia.
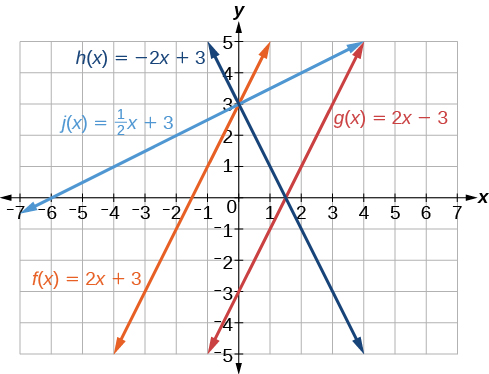
4. Kazi hii ina mteremko wa$\frac{1}{2}$ na y-intercept ya 3. Ni lazima kupita katika hatua (0, 3) na slant juu kutoka kushoto kwenda kulia. Mistari ya I na II hupita$(0, 3)$, lakini mteremko wa$j$ ni chini ya mteremko wa$f$ hivyo mstari kwa$j$ lazima uwe na flatter. Kazi hii inawakilishwa na Line II.

Sasa tunaweza re-studio mistari kama katika Kielelezo$\PageIndex{12}$.

Kielelezo$\PageIndex{12}$

Kutafuta x-intercept ya Line

Hadi sasa, tumekuwa tukipata y-intercepts ya kazi: hatua ambayo grafu ya kazi huvuka mhimili wa y. Kazi inaweza pia kuwa na x-intercept, ambayo ni x-kuratibu ya uhakika ambapo grafu ya kazi huvuka x-axis. Kwa maneno mengine, ni thamani ya pembejeo wakati thamani ya pato ni sifuri.

Ili kupata x-intercept, kuweka kazi$f(x)$ sawa na sifuri na kutatua kwa thamani ya$x$. Kwa mfano, fikiria kazi iliyoonyeshwa.

$$f(x)=3x−6$$

Weka kazi sawa na 0 na kutatua$x$.

$$\begin{align} 0&=3x-6 \\ 6&=3x \\ 2&=x \\ x&=2 \end{align}$$

Grafu ya kazi huvuka x-axis kwa uhakika$(2, 0)$.

Je! Kazi zote za mstari zina x-intercepts?

Kielelezo$\PageIndex{13}$.

Kielelezo$\PageIndex{13}$: Grafu ya$y= 5$.

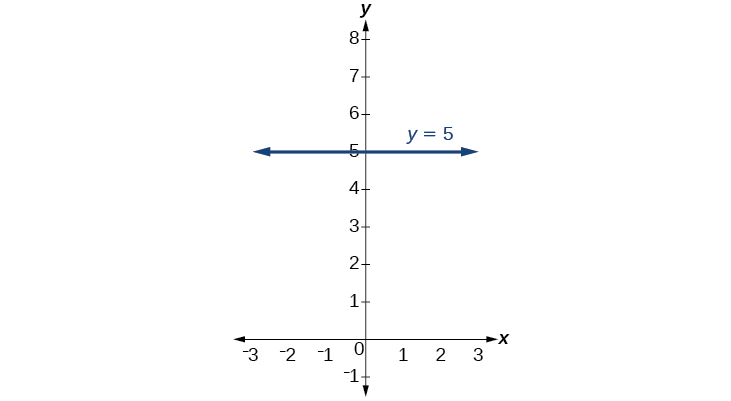
Kumbuka: x-intercept

X-intercept ya kazi ni thamani ya$x$ wakati$f(x)=0$. Inaweza kutatuliwa na equation$0=mx+b$.

Mfano$\PageIndex{5}$​​​​​​​: Finding an x-intercept

Kupata x-intercept ya$f(x)=\frac{1}{2}−3$.

Suluhisho

Weka kazi sawa na sifuri ili kutatua$x$.

$$\begin{align*} 0&=\dfrac{1}{2}x-3 \\ 3&=\dfrac{1}{2}x \\ 6 &= x \\ x&=6 \end{align*}$$

Grafu huvuka mstari wa x-axis kwa uhakika$(6, 0)$.

Uchambuzi

Grafu ya kazi inavyoonyeshwa kwenye Kielelezo$\PageIndex{14}$. Tunaweza kuona kwamba x-intercept ni$(6, 0)$ kama tulivyotarajia.

Kielelezo$\PageIndex{14}$: Grafu ya kazi ya mstari$f(x)=\frac{1}{2}x−3$.

Zoezi$\PageIndex{5}$

Kupata x-intercept ya$f(x)=\frac{1}{4}x−4$.

Jibu

$(16, 0)$

Akielezea mistari ya usawa na ya wima

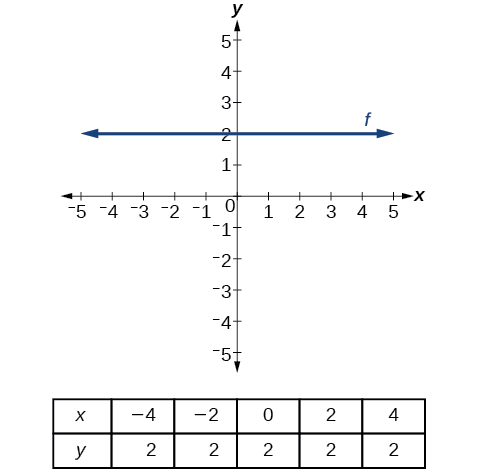
Kuna matukio mawili maalum ya mistari kwenye mistari ya usawa na ya wima. Mstari wa usawa unaonyesha pato la mara kwa mara, au thamani ya y. Katika Kielelezo$\PageIndex{15}$, tunaona kwamba pato ina thamani ya 2 kwa kila thamani ya pembejeo. Mabadiliko katika matokeo kati ya pointi mbili, kwa hiyo, ni 0. Katika formula ya mteremko, namba ni 0, hivyo mteremko ni 0. Kama sisi kutumia$m=0$ katika equation$f(x)=mx+b$, equation simplifies kwa$f(x)=b$. Kwa maneno mengine, thamani ya kazi ni mara kwa mara. Grafu hii inawakilisha kazi$f(x)=2$.

Kielelezo$\PageIndex{15}$: Mstari wa usawa unaowakilisha kazi$f(x)=2$.

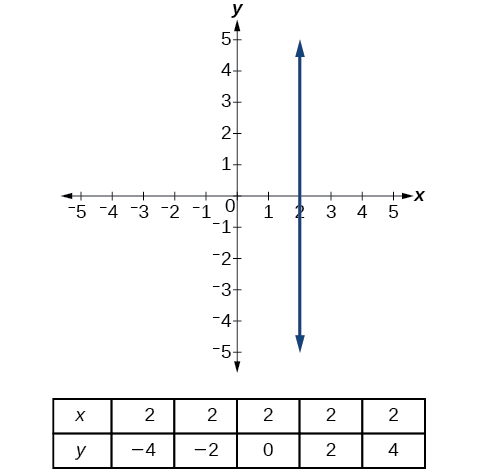
Mstari wa wima unaonyesha pembejeo ya mara kwa mara, au thamani ya x. Tunaweza kuona kwamba thamani ya pembejeo kwa kila hatua kwenye mstari ni 2, lakini thamani ya pato inatofautiana. Kwa sababu thamani hii ya pembejeo imepangwa kwa thamani zaidi ya moja ya pato, mstari wa wima hauwakilishi kazi. Angalia kwamba kati ya pointi mbili, mabadiliko katika maadili ya pembejeo ni sifuri. Katika formula ya mteremko, denominator itakuwa sifuri, hivyo mteremko wa mstari wa wima haujulikani.

Kielelezo$\PageIndex{16}$

Kumbuka kwamba mstari wima, kama vile moja katika Kielelezo$\PageIndex{17}$, ina x-intercept, lakini hakuna y-intercept isipokuwa ni mstari$x=0$. Grafu hii inawakilisha mstari$x=2$.

Kielelezo$\PageIndex{17}$: Mstari wa wima$x=2$, ambao hauwakilishi kazi.

Ufafanuzi: Mistari ya usawa na ya Wima

Mistari inaweza kuwa ya usawa au wima.

• Mstari wa usawa ni mstari unaofafanuliwa na equation katika fomu$f(x)=b$.
• Mstari wa wima ni mstari unaofafanuliwa na equation katika fomu$x=a$.

Mfano$\PageIndex{6}$​​​​​​​: Writing the Equation of a Horizontal Line

Andika equation ya mstari uliowekwa kwenye Kielelezo$\PageIndex{18}$.

Kielelezo$\PageIndex{18}$: Grafu ya$x=7$.

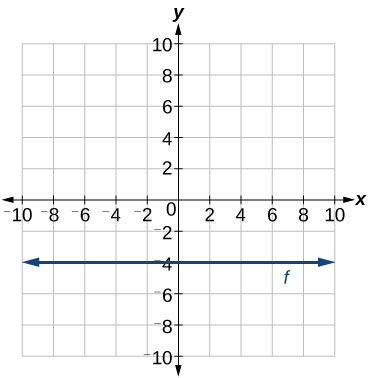
Suluhisho

Kwa thamani yoyote ya x, thamani ya y ni -4, hivyo equation ni$y=−4$.

Mfano$\PageIndex{7}$: Writing the Equation of a Vertical Line

Andika equation ya mstari uliowekwa kwenye Kielelezo$\PageIndex{19}$.

Kielelezo$\PageIndex{19}$: Grafu ya mstari wa wima

Suluhisho

Mara kwa mara x-thamani ni 7, hivyo equation ni$x=7$.

Kuamua Kama mistari ni Sambamba au Perpendicular

mistari miwili katika Kielelezo$\PageIndex{20}$ ni mistari sambamba: wao kamwe intersect. Angalia kwamba wana mwinuko sawa, ambayo inamaanisha mteremko wao ni sawa. Tofauti pekee kati ya mistari miwili ni y-intercept. Ikiwa tumebadilisha mstari mmoja kwa wima kuelekea y-intercept ya nyingine, wangeweza kuwa mstari huo.

\ (y= - (2/3) x +7. Kumbuka kwamba wao ni mistari sambamba.” src=” https://math.libretexts.org/@api/dek...02_02_019n.jpg "/>

Kielelezo\ (\ UkurasaIndex {20}\): Mstari sambamba.

Tunaweza kuamua kutoka kwa equations yao kama mistari miwili ni sambamba kwa kulinganisha mteremko wao. Ikiwa mteremko ni sawa na y-intercepts ni tofauti, mistari ni sawa. Ikiwa mteremko ni tofauti, mistari haifai.

Mchoro$\PageIndex{21}$ ni perpendicular.

Kielelezo$\PageIndex{21}$: Mstari wa pembeni.

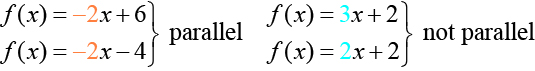
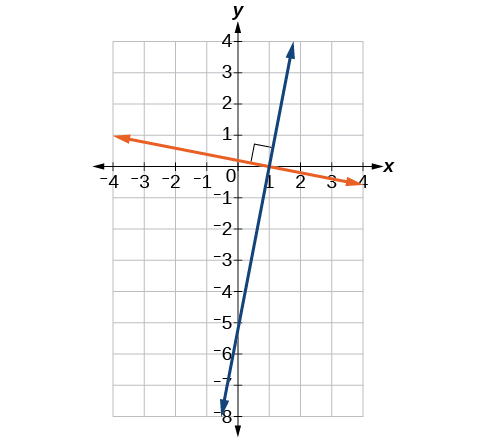
Mstari wa perpendicular hauna mteremko huo. Miteremko ya mistari ya perpendicular ni tofauti na kila mmoja kwa namna fulani. Mteremko wa mstari mmoja ni usawa mbaya wa mteremko wa mstari mwingine. Bidhaa ya nambari na usawa wake ni 1. Hivyo, kama$m_1$ na$m_2$ ni hasi recipurals ya mtu mwingine, wanaweza kuwa tele pamoja na mavuno -1.

$$m_1m_2=−1$$

Ili kupata usawa wa namba, ugawanye 1 kwa nambari. Hivyo usawa wa 8 ni$\frac{1}{8}$, na usawa wa$\frac{1}{8}$ ni 8. Ili kupata usawa usiofaa, kwanza pata usawa na kisha ubadilishe ishara.

Kama ilivyo na mistari sambamba, tunaweza kuamua kama mistari miwili ni perpendicular kwa kulinganisha mteremko wao, kudhani kwamba mistari si usawa wala perpendicular. Mteremko wa kila mstari hapa chini ni usawa mbaya wa mwingine, hivyo mistari ni perpendicular.

$$\begin{align} f(x)&=\dfrac{1}{4}x+2 &\text{negative reciprocal of $\dfrac{1}{4}$ is -4} \\ f(x)&=-4x+3 &\text{negative reciprocal of -4 is $\dfrac{1}{4}$} \end{align}$$

Bidhaa ya mteremko ni —1.

$$−4\Big(\dfrac{1}{4}\Big)=−1$$

Ufafanuzi: Sambamba na Perpendicular

Mstari miwili ni mistari sambamba ikiwa haipatikani. Miteremko ya mistari ni sawa.

$f(x)=m_1x+b_1$na$g(x)=m_2x+b_2$ ni sambamba kama$m_1 = m_2$.

Ikiwa na tu ikiwa$b_1=b_2$ na$m_1=m_2$, tunasema mistari sanjari. Mstari wa mshikamano ni mstari sawa.

Mstari miwili ni mistari ya perpendicular ikiwa huingiliana kwenye pembe za kulia.

$f(x)=m_1x+b_1$na$g(x)=m_2x+b_2$ ni perpendicular kama$m_1m_2=−1$, na hivyo$m_2=\dfrac{−1}{m_1}$.

Mfano$\PageIndex{8}$​​​​​​​: Identifying Parallel and Perpendicular Lines

Kutokana na kazi hapa chini, kutambua kazi ambazo grafu ni jozi ya mistari sambamba na jozi ya mistari perpendicular.

$$\begin{align} f(x)&=2x+3 & h(x)&=-2x+2 \\ g(x)&=\dfrac{1}{2}x-4 & f(x)&=2x-6 \end{align}$$

Suluhisho

Mstari sambamba una mteremko huo. Kwa sababu kazi$f(x)=2x+3$ na$j(x)=2x−6$ kila mmoja zina mteremko wa 2, zinawakilisha mistari sambamba. Mstari wa perpendicular una mteremko usiofaa. Kwa sababu ї2 na$\frac{1}{2}$ ni hasi requirals, equations,$g(x)=\frac{1}{2}x−4$ na$h(x)=−2x+2$ kuwakilisha mistari perpendicular.

Uchambuzi

Grafu ya mistari inavyoonyeshwa kwenye Kielelezo$\PageIndex{22}$.

Kielelezo$\PageIndex{22}$: Grafu ya$h(x)$ (bluu),$f(x)$ (machungwa),$j(x)$ (kijani), na$g(x)$ (nyekundu)

Grafu inaonyesha kwamba mistari$f(x)=2x+3$ na$j(x)=2x–6$ ni sambamba, na mistari$g(x)=\frac{1}{2}x–4$ na$h(x)=−2x+2$ ni perpendicular.

Kuandika Equation ya Mstari Sambamba au Perpendicular kwa Line Kupewa

Kama tunajua equation ya mstari, tunaweza kutumia kile sisi kujua kuhusu mteremko kuandika equation ya mstari kwamba ni ama sambamba au perpendicular kwa mstari fulani.

Kuandika Ulinganisho wa Mistari Sambamba

Tuseme kwa mfano, tunapewa equation ifuatayo.

$$f(x)=3x+1 \nonumber$$

Tunajua kwamba mteremko wa mstari uliofanywa na kazi ni 3. Tunajua pia kwamba y-intercept ni$(0,1)$. Mstari mwingine wowote na mteremko wa 3 utakuwa sawa na$f(x)$. Hivyo mistari iliyoundwa na kazi zote zifuatazo zitakuwa sawa na$f(x)$.

$$\begin{align*} g(x)&=3x+6 \\ h(x)&=3x+1\\ p(x)&=3x+\dfrac{2}{3} \end{align*}$$

Tuseme basi tunataka kuandika equation ya mstari kwamba ni sambamba$f$ na hupita kupitia hatua$(1, 7)$. Tayari tunajua kwamba mteremko ni 3. Tunahitaji tu kuamua ni thamani gani$b$ itatoa mstari sahihi. Tunaweza kuanza na fomu ya mteremko wa equation kwa mstari, na kisha uandike tena katika fomu ya kuingilia mteremko.

$$\begin{align*} y−y_1&=m(x−x_1) \\ y−7&=3(x−1) \\ y−7&=3x−3 \\ y&=3x+4 \end{align*}$$

Hivyo$g(x)=3x+4$ ni sawa na$f(x)=3x+1$ na hupita kupitia hatua$(1, 7)$.

Jinsi ya...

Kutokana na usawa wa kazi na hatua ambayo grafu yake hupita, andika equation ya mstari sambamba na mstari uliopewa unaopita kupitia hatua iliyotolewa.

1. Pata mteremko wa kazi.
2. Badilisha maadili yaliyotolewa katika aidha jumla uhakika-mteremko equation au mteremko intercept equation kwa mstari.
3. Kurahisisha.

Mfano$\PageIndex{9}$: Finding a Line Parallel to a Given Line

Kupata line sambamba na grafu ya$f(x)=3x+6$ kwamba hupita kwa njia ya uhakika$(3, 0)$.

Suluhisho

Mteremko wa mstari uliopewa ni 3. Ikiwa tunachagua fomu ya kuingilia mteremko, tunaweza kubadilisha$m=3$$x=3$, na$f(x)=0$ katika fomu ya kuingilia mteremko ili kupata y-intercept.

$$\begin{align*} g(x)&=3x+b \\ 0&=3(3)+b \\ b&=-9 \end{align*}$$

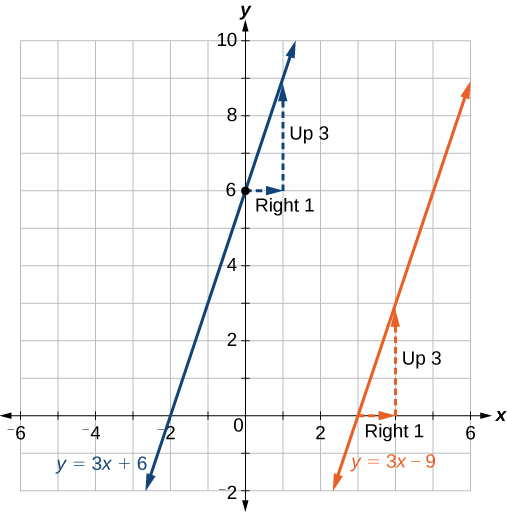
Mstari sambamba na$f(x)$ kwamba hupita kupitia$(3,0)$ ni$g(x)=3x−9$.

Uchambuzi

Tunaweza kuthibitisha kwamba mistari miwili ni sambamba na graphing yao. Kielelezo$\PageIndex{23}$ inaonyesha kwamba mistari miwili kamwe intersect.

Kielelezo$\PageIndex{23}$: Grafu ya kazi mbili ambapo mstari wa bluu ni$y=3x+6$, na mstari wa machungwa ni$y=3x-9$.

Kuandika Ulinganisho wa mistari ya Perpendicular

Tunaweza kutumia mchakato sawa sana kuandika equation kwa mstari perpendicular kwa mstari fulani. Badala ya kutumia mteremko huo, hata hivyo, tunatumia usawa mbaya wa mteremko uliopewa. Tuseme tunapewa kazi ifuatayo:

$$f(x)=2x+4 \nonumber$$

Mteremko wa mstari ni 2, na usawa wake hasi ni$−\frac{1}{2}$. Kazi yoyote na mteremko wa$−\frac{1}{2}$ itakuwa perpendicular kwa$f(x)$. Hivyo mistari iliyoundwa na kazi zote zifuatazo itakuwa perpendicular kwa$f(x)$.

$$\begin{align*} g(x)&=-\dfrac{1}{2}x+4 \\[4pt] h(x)&=-\dfrac{1}{2}x+2 \\[4pt] p(x)&=-\dfrac{1}{2}x-\dfrac{1}{2} \end{align*}$$

Kama kabla, tunaweza kupunguza chini uchaguzi wetu kwa mstari fulani perpendicular kama tunajua kwamba hupita kupitia hatua fulani. Tuseme basi tunataka kuandika equation ya mstari kwamba ni perpendicular$f(x)$ na hupita kupitia hatua$(4, 0)$. Tayari tunajua kwamba mteremko ni$−\frac{1}{2}$. Sasa tunaweza kutumia hatua ya kupata y-intercept kwa kubadilisha maadili yaliyotolewa katika fomu ya mteremko wa mstari na kutatua$b$.

$$\begin{align*} g(x)&=mx+b \\[4pt] 0&=-\dfrac{1}{2}(4)+b \\[4pt] 0 & = -2+b\\[4pt] 2&=b \\ b&=2 \end{align*}$$

Equation kwa kazi na mteremko wa$−\frac{1}{2}$ na y-intercept ya 2 ni

$$g(x)=−\dfrac{1}{2}x+2$$

Hivyo$g(x)=−\frac{1}{2}x+2$ ni perpendicular$f(x)=2x+4$ na hupita kupitia hatua$(4, 0)$. Kuwa na ufahamu kwamba mistari perpendicular inaweza kuangalia wazi perpendicular juu ya graphing calculator isipokuwa sisi kutumia mraba zoom kipengele.

Mstari wa usawa una mteremko wa sifuri na mstari wa wima una mteremko usiojulikana. Mstari huu wawili ni perpendicular, lakini bidhaa ya mteremko wao si —1. Je, ukweli huu si kinyume na ufafanuzi wa mistari perpendicular?

Hapana. Kwa kazi mbili za mstari wa perpendicular, bidhaa za mteremko wao ni -1. Hata hivyo, mstari wa wima sio kazi hivyo ufafanuzi haupingani.

Jinsi ya...

Kutokana na usawa wa kazi na hatua ambayo grafu yake hupita, andika equation ya mstari perpendicular kwa mstari uliopewa.

1. Pata mteremko wa kazi.
2. Kuamua usawa mbaya wa mteremko.
3. Badilisha mteremko mpya na maadili ya$x$ na$y$ kutoka kwa jozi ya kuratibu iliyotolewa ndani$g(x)=mx+b$.
4. Kutatua kwa$b$.
5. Andika equation kwa mstari.

Mfano$\PageIndex{10}$: Finding the Equation of a Perpendicular Line

Kupata equation ya mstari perpendicular$f(x)=3x+3$ kwamba hupita kwa njia ya uhakika$(3, 0)$.

Suluhisho

Mstari wa awali una mteremko$m=3$, hivyo mteremko wa mstari wa perpendicular utakuwa hasi yake ya usawa, au$−\frac{1}{3}$. Kutumia mteremko huu na hatua iliyotolewa, tunaweza kupata equation kwa mstari.

$$\begin{align*} g(x)&= \; –\dfrac{1}{3}x+b \\[4pt] 0&= \; –\dfrac{1}{3}(3)+b \\[4pt] 1&=b \\ b&=1 \end{align*}$$

Mstari wa perpendicular kwa$f(x)$ hiyo hupita kupitia$(3, 0)$ ni$g(x)=−\frac{1}{3}x+1$.

Uchambuzi

Grafu ya mistari miwili inavyoonekana kwenye Mchoro$\PageIndex{24}$ hapa chini.

\ (f (x)\) = 3x + 6.” src=” https://math.libretexts.org/@api/dek...02_02_023n.jpg "/>

Kielelezo$\PageIndex{24}$: Grafu ya kazi mbili ambapo mstari wa bluu ni$g(x)= -\frac{1}{3}x+1$, na mstari wa machungwa ni$f(x)=3x+6$.

Zoezi$\PageIndex{5}$

Kutokana na kazi$h(x)=2x−4$, kuandika equation kwa mstari kupita kwa njia$(0,0)$ hiyo ni

1. sambamba na$h(x)$
2. perpendicular kwa$h(x)$

Jibu

$f(x)=2x$$g(x)=−\frac{1}{2}x$

Jinsi ya...

Kutokana na pointi mbili kwenye mstari na hatua ya tatu, andika equation ya mstari wa perpendicular ambayo hupita kupitia hatua.

1. Kuamua mteremko wa mstari unaopita kupitia pointi.
2. Pata usawa mbaya wa mteremko.
3. Tumia fomu ya kupinga mteremko au fomu ya mteremko ili kuandika equation kwa kubadilisha maadili inayojulikana.
4. Kurahisisha.

Mfano$\PageIndex{11}$: Finding the Equation of a Line Perpendicular to a Given Line Passing through a Point

Mstari unapita kupitia pointi$(−2, 6)$ na$(4,5)$. Pata usawa wa mstari wa perpendicular unaopita kupitia hatua$(4,5)$.

Kutoka kwa pointi mbili za mstari uliopewa, tunaweza kuhesabu mteremko wa mstari huo.

$$\begin{align*} m_1&=\dfrac{5-6}{4−(−2)} \\ &=\dfrac{-1}{6} \\ &=−\dfrac{1}{6} \end{align*}$$

Pata usawa mbaya wa mteremko.

$$\begin{align*} m_2&=\dfrac{-1}{-\dfrac{1}{6}} \\ &=−1\Big(−\dfrac{6}{1}\Big) \\ & =6 \end{align*}$$

Tunaweza kisha kutatua kwa y-intercept ya mstari kupita kupitia hatua$(4,5)$.

$$\begin{align*} g(x)&=6x+b \\ 5&=6(4)+b \\ 5&=24+b \\ −19&=b \\ b&=−19 \end{align*}$$

equation kwa mstari kwamba ni perpendicular kwa mstari kupita kwa njia ya pointi mbili kutokana na pia hupita kupitia hatua$(4,5)$ ni

$$y=6x−19 \nonumber$$

Zoezi$\PageIndex{1}$

Mstari unapita kupitia pointi,$(−2,−15)$ na$(2,−3)$. Kupata equation ya mstari perpendicular kwamba hupita kupitia hatua,$(6,4)$.

Jibu

$y= \; –\dfrac{1}{3}x+6$

Kutatua Mfumo wa Equations ya Mstari Kutumia Grafu

Mfumo wa equations linear ni pamoja na equations mbili au zaidi linear. Grafu za mistari miwili zitaingiliana kwa hatua moja ikiwa sio sambamba. Mistari miwili inayofanana pia inaweza kuingiliana ikiwa ni coincident, ambayo inamaanisha kuwa ni mstari sawa na huingiliana kila wakati. Kwa mistari miwili ambayo si sawa, hatua moja ya makutano itakidhi equations zote mbili na kwa hiyo inawakilisha suluhisho la mfumo.

Ili kupata hatua hii wakati equations wanapewa kama kazi, tunaweza kutatua kwa thamani ya pembejeo ili$f(x)=g(x)$. Kwa maneno mengine, tunaweza kuweka formula kwa mistari sawa na mtu mwingine, na kutatua kwa pembejeo kwamba satisfies equation.

Mfano$\PageIndex{12}$: Finding a Point of Intersection Algebraically

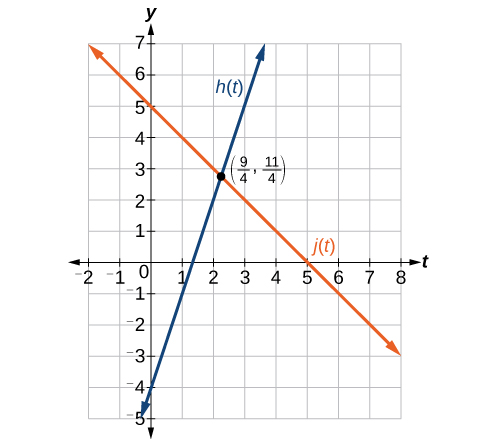
Pata hatua ya makutano ya mistari$h(t)=3t−4$ na$j(t)=5−t$.

Suluhisho

Weka$h(t)=j(t)$.

$$\begin{align} 3t-4&=5-t \\ 4t&=9 \\ t&=\dfrac{9}{4} \end{align}$$

Hii inatuambia mistari intersect wakati pembejeo ni$\frac{9}{4}$.

Tunaweza kisha kupata thamani ya pato ya hatua makutano kwa kutathmini ama kazi katika pembejeo hii.

$$\begin{align} j\Big( \dfrac{9}{4} \Big)&=5-\dfrac{9}{4} \\ &= \dfrac{11}{4}\end{align}$$

Mstari huu huingiliana wakati huo$\Big(\frac{9}{4},\frac{11}{4}\Big)$.

Uchambuzi

Kuangalia Kielelezo$\PageIndex{25}$, matokeo haya inaonekana kuwa ya busara.

Kielelezo$\PageIndex{25}$: Grafu ya kazi mbili$h(t) = 3t - 4$ na$j(t)=t +5$ na makutano yao katika$(\frac{9}{4},\frac{11}{4})$.

Ikiwa tuliulizwa kupata hatua ya makutano ya mistari miwili inayofanana, lazima kitu katika mchakato wa suluhisho kinatuonya ukweli kwamba hakuna ufumbuzi?

Ndiyo. Baada ya kuweka equations mbili sawa na mtu mwingine, matokeo itakuwa utata “$0 = \text{non-zero real number}$”.

Zoezi$\PageIndex{7}$

Angalia grafu katika Kielelezo$\PageIndex{23}$ na utambue zifuatazo kwa kazi$j(t):$

1. y-kukatiza
2. x-intercept (s)
3. mteremko
4. Ni$j(t)$ sambamba au perpendicular kwa$h(t)$ (au wala)?
5. Ni kazi$j(t)$ inayoongezeka au kupungua (au wala)?
6. Andika maelezo ya mabadiliko$j(t)$ kutoka kwa kazi ya kitambulisho cha utambulisho$f(x)=x$.

Jibu

1. $(0,5)$
2. (5,0)
3. Mteremko -1
4. Hakuna sambamba wala perpendic
5. Kupungua kwa kazi
6. Kutokana na kazi ya utambulisho, fanya flip wima (juu ya mhimili wa t) na ugeuke vitengo 5.

Mfano$\PageIndex{13}$: Finding a Break-Even Point

Kampuni inauza helmeti za michezo. Kampuni hiyo inasababisha gharama ya wakati mmoja kwa $250,000. Kila kofia gharama $120 kuzalisha, na kuuza kwa $140.

1. Kupata gharama kazi,$C$, kuzalisha$x$ helmeti, katika dola.
2. Kupata kazi ya mapato,$R$, kutokana na mauzo ya$x$ helmeti, kwa dola.
3. Pata hatua ya kuvunja hata, hatua ya makutano ya grafu mbili$C$ na$R$.

Suluhisho

a. gharama kazi kwa jumla ya gharama za kudumu, $125,000, na gharama variable, $120 kwa kofia.

$C(x)=120x+250,000$

b. kazi ya mapato ni jumla ya mapato kutokana na mauzo ya$x$ helmeti,$R(x)=140x$.

c. kuvunja hata hatua ni hatua ya makutano ya grafu ya gharama na kazi za mapato. Ili kupata x-kuratibu ya jozi ya kuratibu ya hatua ya makutano, weka equations mbili sawa, na kutatua$x$.

$$\begin{align*} C(x)&=R(x) \\ 250,000+120x&=140x \\ 250,000&=20x \\ x&=12,500 \end{align*}$$

Ili kupata$y$, tathmini ama mapato au kazi ya gharama saa 12,500.

$$\begin{align*} R(20)&=140(12,500) \\ &=$1,750,000 \end{align*}$$

Hatua ya kuvunja-hata ni$(12,500,1,750,000)$.

Uchambuzi

Hii inamaanisha kama kampuni inauza helmeti 12,500, huvunja hata; mauzo na gharama zote zilizotumika zilifanana na dola milioni 1.75. Angalia Kielelezo$\PageIndex{26}$.

Kielelezo$\PageIndex{26}$: Grafu ya kazi mbili,$C(x)$ na$R(x)$ ambapo inaonyesha kwamba chini$(12500, 1750000)$ ya kampuni inapoteza fedha na juu ya hatua hiyo kampuni inafanya faida.

Dhana muhimu

• Kazi za mstari zinaweza kupigwa kwa pointi za kupanga au kwa kutumia y-intercept na mteremko.
• Grafu za kazi za mstari zinaweza kubadilishwa kwa kutumia mabadiliko ya juu, chini, kushoto, au kulia, na pia kwa njia ya kunyoosha, compressions, na kutafakari.
• Y-intercept na mteremko wa mstari inaweza kutumika kuandika equation ya mstari.
• X-intercept ni hatua ambayo grafu ya kazi ya mstari huvuka x-axis.
• Mstari wa usawa umeandikwa kwa fomu,$f(x)=b$.
• Mstari wa wima umeandikwa kwa fomu,$x=b$.
• Mstari sambamba una mteremko huo.
• Mstari wa perpendicular una mteremko usiofaa, bila kuchukua wala wima.
• line sambamba na mstari mwingine, kupita kwa njia ya hatua fulani, inaweza kupatikana kwa kubadilisha thamani mteremko wa mstari na x- na y maadili ya uhakika fulani katika equation$f(x)=mx+b$,, na kutumia$b$ kwamba matokeo. Vile vile, fomu ya mteremko wa equation pia inaweza kutumika.
• Mstari unaozingatia mstari mwingine, unaopitia hatua fulani, unaweza kupatikana kwa namna ile ile, isipokuwa kutumia mteremko usiofaa.
• Mfumo wa equations linear inaweza kutatuliwa kuweka equations mbili sawa na mtu mwingine na kutatua kwa$x$. Thamani ya y inaweza kupatikana kwa kutathmini mojawapo ya milinganyo ya awali kwa kutumia thamani hii ya x.
• Mfumo wa usawa wa mstari unaweza pia kutatuliwa kwa kutafuta hatua ya makutano kwenye grafu.

faharasa

usawa line line
inavyoelezwa na$f(x)=b$, ambapo$b$ ni idadi halisi. Mteremko wa mstari usio na usawa ni 0.

mistari sambamba mistari
miwili au zaidi na mteremko huo

mistari ya perpendicular mistari
miwili inayoingiliana kwenye pembe za kulia na ina mteremko ambao ni hasi, usawa wa kila mmoja;

wima line
line inavyoelezwa na$x=a$, ambapo ni idadi halisi. Mteremko wa mstari wa wima haujafafanuliwa.

x-kukatiza uhakika
kwenye grafu ya kazi ya mstari wakati thamani ya pato ni 0; hatua ambayo grafu huvuka mhimili usio na usawa