2.1: Kazi za mstari
- Page ID
- 181422
- Kuwakilisha kazi linear.
- Kuamua kama kazi ya mstari inaongezeka, kupungua, au mara kwa mara.
- Tafsiri mteremko kama kiwango cha mabadiliko.
- Andika na kutafsiri equation kwa kazi linear.
- Graph kazi linear.
- Kuamua kama mistari ni sambamba au perpendicular.
- Andika equation ya mstari sambamba au perpendicular kwa mstari fulani.
Kama ilivyo kwa ukuaji wa mmea wa mianzi, kuna hali nyingi zinazohusisha mabadiliko ya mara kwa mara kwa muda. Fikiria, kwa mfano, treni ya kwanza ya maglev ya kibiashara duniani, Train ya Shanghai MagLev (treni ya maglev duniani, Treni ya Shanghai MagLev (Kielelezo\(\PageIndex{1}\)). Inabeba abiria kwa raha kwa safari ya kilomita 30 kutoka uwanja wa ndege hadi kituo cha Subway kwa dakika nane tu.
Tuseme treni ya maglev ilikuwa kusafiri umbali mrefu, na kwamba treni inao kasi ya mara kwa mara ya mita 83 kwa pili kwa kipindi cha muda mara moja ni mita 250 kutoka kituo. Tunawezaje kuchambua umbali wa treni kutoka kituo kama kazi ya muda? Katika sehemu hii, tutachunguza aina ya kazi ambayo ni muhimu kwa kusudi hili, na kuitumia kuchunguza hali halisi ya ulimwengu kama umbali wa treni kutoka kituo cha wakati fulani katika time.Maglev treni walikuwa kusafiri umbali mrefu, na kwamba treni inao kasi ya mara kwa mara ya mita 83 kwa sekunde kwa kipindi cha muda mara moja ni mita 250 kutoka kituo hicho. Tunawezaje kuchambua umbali wa treni kutoka kituo kama kazi ya muda? Katika sehemu hii, tutachunguza aina ya kazi ambayo ni muhimu kwa kusudi hili, na kuitumia kuchunguza hali halisi ya ulimwengu kama umbali wa treni kutoka kituo cha wakati fulani.
Kuwakilisha Kazi za Linear
Kazi inayoelezea mwendo wa treni ni kazi ya mstari, ambayo hufafanuliwa kama kazi na kiwango cha mabadiliko ya mara kwa mara, yaani, polynomial ya shahada ya 1. Kuna njia kadhaa za kuwakilisha kazi ya mstari, ikiwa ni pamoja na fomu ya neno, alama ya kazi, fomu ya tabular, na fomu ya kielelezo. Tutaelezea mwendo wa treni kama kazi kwa kutumia kila njia.
Inawakilisha Kazi ya Linear katika Fomu ya Neno
Hebu tuanze kwa kuelezea kazi ya mstari kwa maneno. Kwa tatizo treni sisi tu kuchukuliwa, neno zifuatazo hukumu inaweza kutumika kuelezea uhusiano kazi.
- Umbali wa treni kutoka kituo ni kazi ya wakati ambapo treni huenda kwa kasi ya mara kwa mara pamoja na umbali wake wa awali kutoka kituo wakati ilianza kusonga kwa kasi ya mara kwa mara.
Kasi ni kiwango cha mabadiliko. Kumbuka kwamba kiwango cha mabadiliko ni kipimo cha jinsi mabadiliko ya kutofautiana kwa tegemezi yanavyobadilika kwa heshima na kutofautiana kwa kujitegemea. Kiwango cha mabadiliko kwa mfano huu ni mara kwa mara, ambayo ina maana kwamba ni sawa kwa kila thamani ya pembejeo. Wakati (pembejeo) huongezeka kwa pili ya pili, umbali unaofanana (pato) huongezeka kwa mita 83. Treni ilianza kusonga kwa kasi hii ya mara kwa mara kwa umbali wa mita 250 kutoka kituo.
Inawakilisha Kazi ya Linear katika Uthibitishaji wa Kazi
Njia nyingine ya kuwakilisha kazi za mstari ni kwa kutumia alama ya kazi. Mfano mmoja wa uthibitishaji wa kazi ni equation iliyoandikwa katika fomu inayojulikana kama mteremka-intercept fomu ya mstari, ambapo xis thamani ya pembejeo,\(m\) ni kiwango cha mabadiliko, na\(b\) ni thamani ya awali ya kutofautiana tegemezi.
\[\begin{align*} &\text{Equation form } &y=mx+b \\[4pt] &\text{Equation notation } &f(x)=mx+b \end{align*}\]
Katika mfano wa treni, tunaweza kutumia nukuu\(D(t)\) ambayo umbali wa jumla\(D\) ni kazi ya wakati\(t\). Kiwango,\(m\), ni mita 83 kwa pili. Thamani ya awali ya kutofautiana kwa tegemezi\(b\) ni umbali wa awali kutoka kituo, mita 250. Tunaweza kuandika equation ya jumla ili kuwakilisha mwendo wa treni.
\[D(t)=83t+250\]
Inawakilisha Kazi ya Linear katika Fomu ya Tabular
Njia ya tatu ya kuwakilisha kazi ya mstari ni kupitia matumizi ya meza. uhusiano kati ya umbali kutoka kituo na wakati ni kuwakilishwa katika Kielelezo\(\PageIndex{2}\). Kutoka meza, tunaweza kuona kwamba umbali unabadilika kwa mita 83 kwa kila ongezeko la pili la pili kwa wakati.
Hapana. Pembejeo inawakilisha wakati, hivyo wakati nambari zisizo za busara na zisizofaa zinawezekana, namba halisi hasi haziwezekani kwa mfano huu. Pembejeo ina idadi isiyo ya hasi halisi.
Inawakilisha Kazi ya Linear katika Fomu ya Picha
Njia nyingine ya kuwakilisha kazi za mstari ni kuibua, kwa kutumia grafu. Tunaweza kutumia uhusiano kazi kutoka juu, kuteka grafu\(D(t)=83t+250\), kuwakilishwa katika Kielelezo\(\PageIndex{3}\). Angalia grafu ni mstari. Tunapopanga kazi ya mstari, grafu daima ni mstari.
Kiwango cha mabadiliko, ambayo ni mara kwa mara, huamua slant, au mteremko wa mstari. Hatua ambayo thamani ya pembejeo ni sifuri ni intercept wima, au y-intercept, ya mstari. Tunaweza kuona kutoka grafu katika Kielelezo\(\PageIndex{3}\) kwamba y-intercept katika mfano treni sisi tu aliona ni\((0,250)\) na inawakilisha umbali wa treni kutoka kituo wakati ilianza kusonga kwa kasi ya mara kwa mara.
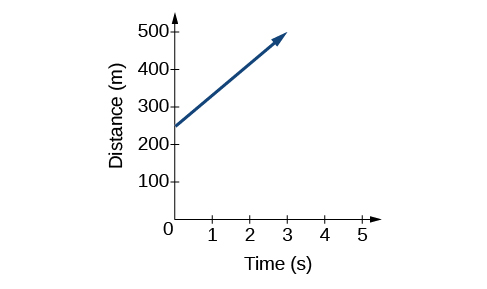
Kumbuka kwamba grafu ya mfano treni ni vikwazo, lakini hii si mara zote kesi. Fikiria grafu ya mstari\(f(x)=2x+1\). Jiulize namba gani zinaweza kuingizwa kwenye kazi, yaani, uwanja wa kazi ni nini? Kikoa kinajumuisha namba zote halisi kwa sababu nambari yoyote inaweza kuwa mara mbili, na kisha uwe na moja iliyoongezwa kwenye bidhaa.
Kazi ya mstari ni kazi ambayo grafu ni mstari. Kazi za mstari zinaweza kuandikwa katika fomu ya mteremko wa mstari
\[f(x)=mx+b\]
\(b\)wapi thamani ya awali au ya kuanzia ya kazi (wakati wa pembejeo,\(x=0\)), na\(m\) ni kiwango cha mabadiliko ya mara kwa mara, au mteremko wa kazi. Y-intercept iko\((0,b)\).
shinikizo,\(P\), katika paundi kwa inchi mraba (PSI) juu ya diver katika Kielelezo\(\PageIndex{4}\) inategemea kina chake chini ya uso wa maji,\(d\), katika miguu. Uhusiano huu unaweza kuwa inatokana na equation,\(P(d)=0.434d+14.696\). Rejesha tena kazi hii kwa maneno.
Ili kurejesha kazi kwa maneno, tunahitaji kuelezea kila sehemu ya equation. Shinikizo kama kazi ya kina ni sawa na mia nne thelathini na nne elfu mara kina pamoja na kumi na nne na mia sita tisini na sita elfu.
Uchambuzi
Thamani ya awali, 14.696, ni shinikizo katika PSI kwenye diver kwa kina cha miguu 0, ambayo ni uso wa maji. Kiwango cha mabadiliko, au mteremko, ni 0.434 PSI kwa mguu. Hii inatuambia kwamba shinikizo la diver huongezeka 0.434 PSI kwa kila mguu kina chake kinaongezeka.
Kuamua kama Kazi ya Linear Inaongezeka, Kupungua, au Mara kwa mara
kazi linear sisi kutumika katika mifano miwili ya awali iliongezeka baada ya muda, lakini si kila kazi linear gani. Kazi ya mstari inaweza kuongezeka, kupungua, au mara kwa mara. Kwa kazi inayoongezeka, kama ilivyo kwa mfano wa treni, maadili ya pato huongezeka kama maadili ya pembejeo yanavyoongezeka. Grafu ya kazi inayoongezeka ina mteremko mzuri. Mstari na mteremko mzuri hupanda juu kutoka kushoto kwenda kulia kama kwenye Mchoro\(\PageIndex{5}\) (a). Kwa kazi ya kupungua, mteremko ni hasi. Maadili ya pato hupungua kama maadili ya pembejeo yanaongezeka. Mstari na mteremko hasi hupanda chini kutoka kushoto kwenda kulia kama kwenye Mchoro\(\PageIndex{5}\) (b). Ikiwa kazi ni mara kwa mara, maadili ya pato ni sawa kwa maadili yote ya pembejeo hivyo mteremko ni sifuri. Mstari na mteremko wa sifuri ni usawa kama kwenye Mchoro\(\PageIndex{5}\) (c).
![Grafu tatu zinazoonyesha kazi inayoongezeka, kazi ya kupungua, na kazi ya mara kwa mara.] Kuongezeka na Kupungua Kazi](https://math.libretexts.org/@api/deki/files/1061/CNX_Precalc_Figure_02_01_004abc.jpg)
Kuongezeka na Kupungua Kazi
Kuongezeka na Kupungua Kazi
Mteremko huamua kama kazi ni kazi inayoongezeka ya mstari, kazi ya kupungua kwa mstari, au kazi ya mara kwa mara.
- \(f(x)=mx+b\)ni kazi ya kuongeza kama\(m>0\).
- \(f(x)=mx+b\)ni kazi kupungua kama\(m<0\).
- \(f(x)=mx+b\)ni kazi ya mara kwa mara kama\(m=0\).
Baadhi ya tafiti za hivi karibuni zinaonyesha kwamba kijana hutuma wastani wa maandiko 60 kwa siku. Kwa kila moja ya matukio yafuatayo, tafuta kazi ya mstari inayoelezea uhusiano kati ya thamani ya pembejeo na thamani ya pato. Kisha, onyesha kama grafu ya kazi inaongezeka, kupungua, au mara kwa mara.
- Idadi ya maandiko ambayo kijana hutuma inachukuliwa kuwa kazi ya muda kwa siku. Pembejeo ni idadi ya siku, na pato ni jumla ya idadi ya maandiko yaliyotumwa.
- Kijana ana kikomo cha maandiko 500 kwa mwezi katika mpango wake wa data. Pembejeo ni idadi ya siku, na pato ni jumla ya idadi ya maandiko iliyobaki kwa mwezi.
- Kijana ana idadi isiyo na ukomo wa maandiko katika mpango wake wa data kwa gharama ya $50 kwa mwezi. pembejeo ni idadi ya siku, na pato ni gharama ya jumla ya texting kila mwezi.
Suluhisho
Kuchambua kila kazi.
- Kazi inaweza kuwakilishwa kama\(f(x)=60x\)\(x\) wapi idadi ya siku. Mteremko, 60, ni chanya hivyo kazi inaongezeka. Hii ina maana kwa sababu idadi ya maandiko huongezeka kwa kila siku.
- Kazi inaweza kuwakilishwa kama\(f(x)=500−60x\)\(x\) wapi idadi ya siku. Katika kesi hiyo, mteremko ni hasi, hivyo kazi inapungua. Hii ina maana kwa sababu idadi ya maandiko iliyobaki inapungua kila siku na kazi hii inawakilisha idadi ya maandiko yaliyobaki katika mpango wa data baada ya\(x\) siku.
- Kazi ya gharama inaweza kuwakilishwa kama\(f(x)=50\) kwa sababu idadi ya siku haiathiri gharama ya jumla. Mteremko ni 0 hivyo kazi ni mara kwa mara.
Kuhesabu na kutafsiri mteremko
Katika mifano tumeona hadi sasa, tumekuwa na mteremko zinazotolewa kwa ajili yetu. Hata hivyo, mara nyingi tunahitaji kuhesabu mteremko uliotolewa na maadili ya pembejeo na pato. Kutokana na maadili mawili kwa pembejeo,\(x_1\) na\(x_2\), na maadili mawili yanayofanana kwa pato,\(y_2\) na-ambayo inaweza kuwakilishwa\(y_1\) na seti ya pointi,\((x_1,y_1)\) na\((x_2,y_2)\) - tunaweza kuhesabu mteremko\(m\), kama ifuatavyo
\[\begin{align*} m &= \dfrac{\text{change in output (rise)}}{ \text{change in input (run)}} \\[4pt] &= \dfrac{{\Delta}y}{ {\Delta}x} = \dfrac{y_2−y_1}{x_2−x_1} \end{align*}\]
\({\Delta}y\)wapi makazi ya wima na\({\Delta}x\) ni makazi ya usawa. Kumbuka katika nukuu ya kazi maadili mawili yanayofanana\(y_2\) kwa pato\(y_1\) na kwa kazi\(f\)\(y_2=f(x_2)\),\(y_1=f(x_1)\) na, ili tuweze kuandika sawa
\[m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1} \nonumber\]
Kielelezo\(\PageIndex{6}\) kinaonyesha jinsi mteremko wa mstari kati ya pointi,\((x_1,y_1)\) na\((x_2,y_2)\), umehesabiwa. Kumbuka kwamba mteremko hupima mwinuko. Thamani kubwa kabisa ya mteremko, mstari mkali ni.
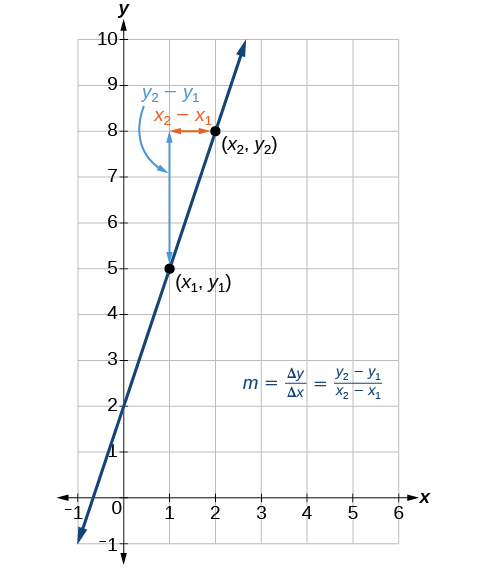
Je, vitengo vya mteremko daima\(\frac{\text{units for the output}}{ \text{units for the input}}\)?
Ndiyo. Fikiria vitengo kama mabadiliko ya thamani ya pato kwa kila kitengo cha mabadiliko katika thamani ya pembejeo. Mfano wa mteremko inaweza kuwa maili kwa saa au dola kwa siku. Angalia vitengo kuonekana kama uwiano wa vitengo kwa pato kwa vitengo kwa pembejeo.
Mteremko, au kiwango cha mabadiliko, ya kazi\(m\) inaweza kuhesabiwa kulingana na yafuatayo:
\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\]
wapi\(x_1\) na\(x_2\) ni maadili ya pembejeo,\(y_1\) na\(y_2\) ni maadili ya pato.
Kutokana na pointi mbili kutoka kwa kazi ya mstari, hesabu na kutafsiri mteremko.
- Tambua vitengo vya maadili ya pato na pembejeo.
- Tumia mabadiliko ya maadili ya pato na mabadiliko ya maadili ya pembejeo.
- Tafsiri mteremko kama mabadiliko katika maadili ya pato kwa kitengo cha thamani ya pembejeo.
Kama\(f(x)\) ni kazi linear,\((3,−2)\) na\((8,1)\) ni pointi kwenye mstari, kupata mteremko. Je, kazi hii inaongezeka au kupungua?
Suluhisho
Jozi za kuratibu ni\((3,−2)\) na\((8,1)\). Ili kupata kiwango cha mabadiliko, tunagawanya mabadiliko katika pato na mabadiliko katika pembejeo.
\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{1-(-2)}{8-3}=\dfrac{3}{5}\]
Tunaweza pia kuandika mteremko kama\(m=0.6\). Kazi inaongezeka kwa sababu\(m>0\).
Uchambuzi
Kama ilivyoelezwa hapo awali, utaratibu ambao tunaandika pointi haijalishi wakati sisi compute mteremko wa mstari kwa muda mrefu kama thamani ya kwanza ya pato, au y -kuratibu, kutumika sambamba na thamani ya kwanza ya pembejeo, au x -kuratibu, kutumika.
Kama\(f(x)\) ni kazi linear,\((2, 3)\) na\((0,4)\) ni pointi kwenye mstari, kupata mteremko. Je, kazi hii inaongezeka au kupungua?
- Jibu
-
\(m=\frac{4−3}{0−2} =\frac{1}{-2}=-\frac{1}{2}\); kupungua kwa sababu\(m<0\).
Idadi ya wakazi wa mji iliongezeka kutoka 23,400 hadi 27,800 kati ya 2008 na 2012. Kupata mabadiliko ya idadi ya watu kwa mwaka kama sisi kudhani mabadiliko mara kwa mara kutoka 2008 kwa 2012.
Kiwango cha mabadiliko kinahusiana na mabadiliko katika idadi ya watu na mabadiliko ya wakati. Idadi ya watu iliongezeka kwa\(27,800−23,400=4400\) watu zaidi ya muda wa miaka minne. Ili kupata kiwango cha mabadiliko, ugawanye mabadiliko katika idadi ya watu kwa idadi ya miaka.
\[\dfrac{4,400 \text{ people}}{4 \text{ years}} =1,100 \dfrac{\text{people}}{\text{year}}\]
Hivyo idadi ya watu iliongezeka kwa watu 1,100 kwa mwaka.
Uchambuzi
Kwa sababu tunaambiwa kuwa idadi ya watu iliongezeka, tunatarajia mteremko kuwa chanya. Hii mteremko chanya sisi mahesabu kwa hiyo ni busara.
Idadi ya wakazi wa mji mdogo iliongezeka kutoka 1,442 hadi 1,868 kati ya 2009 na 2012. Kupata mabadiliko ya idadi ya watu kwa mwaka kama sisi kudhani mabadiliko mara kwa mara kutoka 2009 kwa 2012.
- Jibu
-
\(m=\frac{1,868−1,442}{2,012−2,009} = \frac{426}{3} =\text{ 142 people per year}\)
Kuandika Fomu ya Point-Slope ya Equation ya Linear
Hadi sasa, tumekuwa tukitumia fomu ya mteremka-intercept ya equation linear kuelezea kazi linear. Hapa, tutajifunza njia nyingine ya kuandika kazi ya mstari, fomu ya mteremko.
\[y-y_1=m(x-x_1)\]
Fomu ya mteremko wa uhakika inatokana na formula ya mteremko.
\[ \begin{align*} &m=\dfrac{y-y_1}{x-x_1} &\text{assuming }x{\neq}x_1 \\ &m(x-x_1)=\dfrac{y-y_1}{x-x_1}(x-x_1) &\text{Multiply both sides by }(x-x_1). \\ &m(x-x_1)=y-y_1 &\text{Simplify} \\ &y-y_1=m(x-x_1) &\text{Rearrange} \end{align*}\]
Kumbuka kwamba fomu ya kuingilia mteremko na fomu ya mteremko wa uhakika inaweza kutumika kuelezea kazi sawa. Tunaweza kuhamia kutoka fomu moja hadi nyingine kwa kutumia algebra ya msingi. Kwa mfano, tuseme tunapewa equation katika fomu ya hatua-mteremko,\(y−4=− \frac{1}{2}(x−6)\). Tunaweza kubadilisha kwa fomu mteremka-intercept kama inavyoonekana.
\[\begin{align*} y-4&=-\dfrac{1}{2}(x-6) \\ y-4&=-\dfrac{1}{2}x+3 &\text{Distribute the }-\dfrac{1}{2}. \\ y&=-\dfrac{1}{2}x+7 &\text{Add 4 to each side.}\end{align*}\]
Kwa hiyo, mstari huo unaweza kuelezewa katika fomu ya kuingilia mteremko kama\(y=\dfrac{1}{2}x+7\).
Fomu ya mteremko wa uhakika wa equation ya mstari inachukua fomu
\[y-y_1=m(x−x_1)\]
wapi\(m\) mteremko,\(x_1\) na\(y_1\) ni\(x\) na\(y\) kuratibu ya hatua maalum kwa njia ambayo mstari hupita.
Kuandika Equation ya Mstari Kutumia Point na Slope
Fomu ya mteremko wa uhakika ni muhimu hasa ikiwa tunajua hatua moja na mteremko wa mstari. Tuseme, kwa mfano, tunaambiwa kuwa mstari una mteremko wa 2 na hupita kupitia hatua\((4,1)\). Tunajua kwamba\(m=2\) na kwamba\(x_1=4\) na\(y_1=1\). Tunaweza kubadilisha maadili haya katika equation ya jumla ya hatua-mteremko.
\[\begin{align*} y−y_1&=m(x−x_1) \\ y−1&=2(x−4) \end{align*}\]
Kama tulitaka kisha kuandika upya equation katika mteremka-intercept fomu, sisi kutumia mbinu algebraic.
\[\begin{align*} y−1&=2(x−4) \\ y−1&=2x−8 &\text{Distribute the 2.} \\ y&=2x−7 &\text{Add 1 to each side.} \end{align*}\]
Wote equations,\(y−1=2(x−4)\) na\(y=2x–7\), kuelezea mstari huo. Angalia Kielelezo\(\PageIndex{7}\).
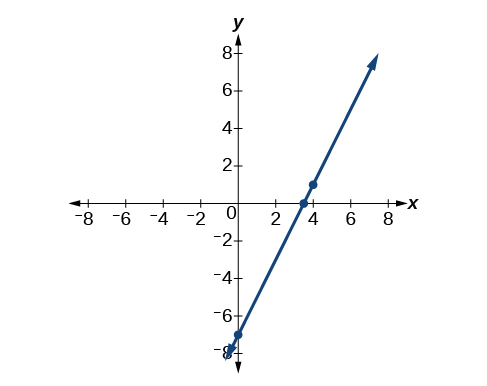
Andika fomu ya mteremko wa equation ya mstari na mteremko wa 3 unaopita kupitia hatua\((6,–1)\). Kisha uandike tena katika fomu ya kuingilia mteremko.
Suluhisho
Hebu tuchunguze kile tunachojua kutokana na habari iliyotolewa. Mteremko ni 3, hivyo\(m=3\). Pia tunajua hatua moja, hivyo tunajua\(x_1=6\) na\(y_1 =−1\). Sasa tunaweza kubadilisha maadili haya katika equation ya jumla ya hatua-mteremko.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y−(−1)&=3(x−6) &\text{Substitute known values.} \\ y+1&=3(x−6) &\text{Distribute −1 to find point-slope form.} \end{align*}\]
Kisha tunatumia algebra ili kupata fomu ya kuingilia mteremko.
\[\begin{align*} y+1&=3(x−6) \\ y+1&=3x−18 &\text{Distribute 3.} \\ y&=3x−19 &\text{Simplify to slope-intercept form.} \end{align*}\]
Andika fomu ya mteremko wa equation ya mstari na mteremko wa —2 unaopitia hatua\((–2, 2)\). Kisha uandike tena katika fomu ya kuingilia mteremko.
- Jibu
-
\(y−2=−2(x+2)\);\(y=−2x−2\)
Kuandika Equation ya Mstari Kutumia Pointi mbili
Aina ya mteremko wa equation pia ni muhimu kama tunajua pointi mbili ambazo mstari hupita. Tuseme, kwa mfano, tunajua kwamba mstari unapita kupitia pointi\((0, 1)\) na\((3, 2)\). Tunaweza kutumia kuratibu ya pointi mbili ili kupata mteremko.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{2-1}{3-0} \\ &=\dfrac{1}{3} \end{align*}\]
Sasa tunaweza kutumia mteremko sisi kupatikana na kuratibu ya moja ya pointi kupata equation kwa line. Hebu kutumia\((0,1)\) kwa uhakika wetu.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=\dfrac{1}{3}(x-0) \end{align*}\]
Kama kabla, tunaweza kutumia algebra kuandika upya equation katika fomu mteremka-intercept.
\[\begin{align*} y-1&=\dfrac{1}{3}(x-0) \\ y-1&=\dfrac{1}{3}x &\text{Distribute the }\dfrac{1}{3}. \\ y&=\dfrac{1}{3}x+1 &\text{Add 1 to each side.} \end{align*}\]
Wote equations kuelezea mstari inavyoonekana katika Kielelezo\(\PageIndex{8}\).
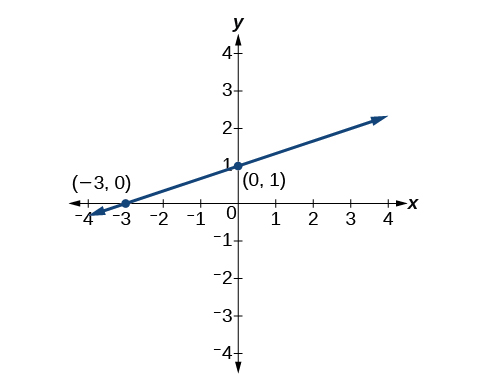
Andika fomu ya mteremko wa equation ya mstari unaopita kupitia pointi\((5,1)\) na\((8, 7)\). Kisha uandike tena katika fomu ya kuingilia mteremko.
Hebu tuanze kwa kutafuta mteremko.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{7-1}{8-5} \\ &=\dfrac{6}{3} \\ &= 2 \end{align*}\]
Hivyo\(m=2\). Kisha, tunabadilisha mteremko na kuratibu kwa moja ya pointi katika usawa wa jumla wa mteremko. Tunaweza kuchagua hatua yoyote, lakini tutatumia\((5,1)\).
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=2(x-5) \end{align*}\]
Equation ya mteremko wa mstari ni\(y_2–1=2(x_2–5)\). Ili kuandika upya equation katika fomu ya mteremka-intercept, tunatumia algebra.
\[\begin{align*} y-1&=2(x-5) \\ y-1&=2x-10 \\ y&=2x-9 \end{align*}\]
Mlinganyo wa mteremko wa mstari ni\(y=2x–9\).
\(\PageIndex{4}\): Andika uhakika-mteremko fomu ya equation ya mstari kwamba hupita kwa njia ya pointi\((–1,3)\) na\((0,0)\). Kisha uandike tena katika fomu ya kuingilia mteremko.
Suluhisho
\(y−0=−3(x−0)\);\(y=−3x\)
Kuandika na Kutafsiri Equation kwa Kazi ya Linear
Sasa kwa kuwa tumeandika equations kwa kazi za mstari katika fomu zote za mteremko na fomu ya mteremko, tunaweza kuchagua njia gani ya kutumia kulingana na habari tunayopewa. Taarifa hiyo inaweza kutolewa kwa namna ya grafu, hatua na mteremko, pointi mbili, na kadhalika. Angalia grafu ya kazi\(f\) katika Kielelezo\(\PageIndex{9}\).
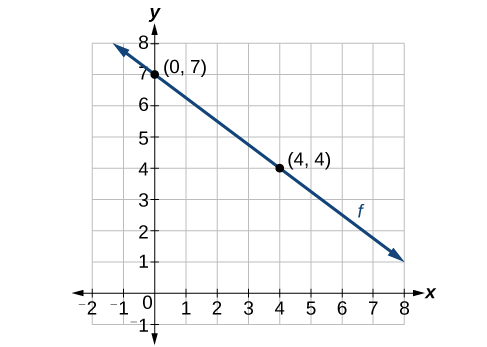
Hatupewa mteremko wa mstari, lakini tunaweza kuchagua pointi mbili kwenye mstari ili kupata mteremko. Hebu kuchagua\((0,7)\) na\((4, 4)\). Tunaweza kutumia pointi hizi kuhesabu mteremko.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{4-7}{4-0} \\&=-\dfrac{3}{4}\end{align*}\]
Sasa tunaweza kubadilisha mteremko na kuratibu za moja ya pointi katika fomu ya mteremko wa uhakika.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-4&=-\dfrac{3}{4}(x-4) \end{align*}\]
Kama tunataka kuandika upya equation katika fomu mteremka-intercept, tunataka kupata
\[\begin{align*} y-4&=-\dfrac{3}{4}(x-4) \\ y-4 &=-\dfrac{3}{4}x+3 \\ y&=-\dfrac{3}{4}x+7\end{align*}\]
Ikiwa tulitaka kupata fomu ya kuingilia mteremko bila kuandika fomu ya mteremko wa kwanza, tungeweza kutambua kwamba mstari unavuka mhimili wa y wakati thamani ya pato ni 7. Kwa hiyo,\(b=7\). Sasa tuna thamani ya awali\(b\) na mteremko\(m\) ili tuweze kubadilisha\(m\) na\(b\) ndani ya fomu ya mteremko wa mstari.
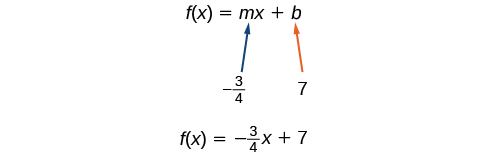
Hivyo kazi ni\(f(x)=−\frac{3}{4}x+7\), na equation linear itakuwa\(y=−\frac{3}{4}x+7\).
Kutokana na grafu ya kazi ya mstari, weka equation ili kuwakilisha kazi.
- Tambua pointi mbili kwenye mstari.
- Tumia pointi mbili kuhesabu mteremko.
- Tambua wapi mstari unavuka mhimili wa y ili kutambua y-intercept kwa ukaguzi wa visu.
- Badilisha mteremko na y-kuingilia ndani ya fomu ya mteremko wa mstari wa mstari.
Andika equation kwa kazi linear kutokana grafu ya\(f\) inavyoonekana katika Kielelezo\(\PageIndex{11}\).
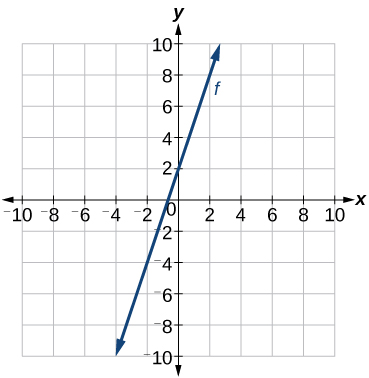
Suluhisho
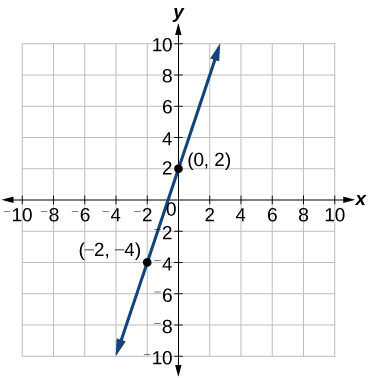
Tambua pointi mbili kwenye mstari, kama vile\((0, 2)\) na\((−2,−4)\). Tumia pointi kuhesabu mteremko.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{4-2}{-2-0} \\ &=\dfrac{-6}{-2} \\ &=3 \end{align*}\]
Kuweka mteremko na kuratibu za moja ya pointi katika fomu ya mteremko.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-(-4)&=3(x-(-2)) \\ y+4 &= 3(x+2)\end{align*}\]
Tunaweza kutumia algebra kuandika upya equation katika fomu mteremka-intercept.
\[\begin{align*} y+4&= 3(x+2) \\ y+4&= 3x+6 \\ y & = 3x + 2 \end{align*}\]
Uchambuzi
Hii mantiki kwa sababu tunaweza kuona kutoka Kielelezo\(\PageIndex{12}\) kwamba line misalaba y mhimili katika hatua\((0, 2)\), ambayo ni y-intercept, hivyo\(b=2\).
Tuseme Ben anaanza kampuni ambayo yeye incurs gharama fasta ya $1,250 kwa mwezi kwa ajili ya uendeshaji, ambayo ni pamoja na ofisi yake kodi. Gharama zake za uzalishaji ni $37.50 kwa kila kitu. Andika kazi linear\(C\) ambapo\(C(x)\) ni gharama ya\(x\) vitu zinazozalishwa katika mwezi fulani.
Suluhisho
Gharama za kudumu zipo kila mwezi, $1,250. Gharama ambazo zinaweza kutofautiana ni pamoja na gharama za kuzalisha kila kitu, ambacho ni $37.50 kwa Ben. Gharama ya kutofautiana, inayoitwa gharama ndogo, inawakilishwa na 37.5. Gharama Ben incurs ni jumla ya gharama hizi mbili, kuwakilishwa na\(C(x)=1250+37.5x\).
Uchambuzi
Kama Ben inazalisha vitu 100 katika mwezi, gharama yake ya kila mwezi ni kuwakilishwa na
\[\begin{align*} C(100)&=1250+37.5(100) \\ &=5000 \end{align*}\]
Hivyo gharama yake ya kila mwezi itakuwa $5,000.
Kama\(f\) ni kazi linear, na\(f(3)=−2\), na\(f(8)=1\), kupata equation kwa ajili ya kazi katika mteremka-intercept fomu.
Suluhisho
Tunaweza kuandika pointi zilizotolewa kwa kutumia kuratibu.
\[\begin{align*} f(3)&= -2{\rightarrow}(3,2) \\ f(8)&=1{\rightarrow}(8,1) \end{align*}\]
Tunaweza kutumia pointi kuhesabu mteremko.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{1-(-2)}{8-3} \\ &=\dfrac{3}{5} \end{align*}\]
Kuweka mteremko na kuratibu za moja ya pointi katika fomu ya mteremko.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-(-2)&=\dfrac{3}{5}(x-3) \end{align*}\]
Tunaweza kutumia algebra kuandika upya equation katika fomu mteremka-intercept.
\[\begin{align*} y+2&=\dfrac{3}{5}(x-3) \\ y+2&=\dfrac{3}{5}x-\dfrac{9}{5} \\ y&=\dfrac{3}{5}x-\dfrac{19}{5} \end{align*}\]
Kama\(f(x)\) ni kazi linear, na\(f(2)=–11\), na\(f(4)=−25\), kupata equation kwa ajili ya kazi katika mteremka-intercept fomu.
- Jibu
-
\(y=−7x+3\)
Mfano wa Matatizo ya Ulimwengu halisi na Kazi za
Katika ulimwengu wa kweli, matatizo si mara zote yaliyotajwa wazi kwa suala la kazi au kuwakilishwa na grafu. Kwa bahati nzuri, tunaweza kuchambua tatizo kwa kwanza anayewakilisha kama kazi linear na kisha kutafsiri vipengele vya kazi. Muda mrefu kama sisi kujua, au unaweza kufikiri, thamani ya awali na kiwango cha mabadiliko ya kazi linear, tunaweza kutatua aina mbalimbali ya matatizo halisi ya dunia.
Kutokana na kazi ya mstari\(f\) na thamani ya awali na kiwango cha mabadiliko, tathmini\(f(c)\).
- Kuamua thamani ya awali na kiwango cha mabadiliko (mteremko).
- Badilisha maadili katika\(f(x)=mx+b\).
- Tathmini kazi katika\(x=c\).
Marcus kwa sasa ana nyimbo 200 katika mkusanyiko wake wa muziki. Kila mwezi, anaongeza nyimbo 15 mpya. Andika formula kwa idadi ya nyimbo\(N\),, katika mkusanyiko wake kama kazi ya muda\(t\),, idadi ya miezi. Ni nyimbo ngapi atakayekuwa na mwaka?
Suluhisho
Thamani ya awali ya kazi hii ni 200 kwa sababu kwa sasa anamiliki nyimbo 200, hivyo\(N(0)=200\), ambayo ina maana kwamba\(b=200\).
Idadi ya nyimbo huongezeka kwa nyimbo 15 kwa mwezi, hivyo kiwango cha mabadiliko ni nyimbo 15 kwa mwezi. Kwa hiyo tunajua hilo\(m=15\). Tunaweza kubadilisha thamani ya awali na kiwango cha mabadiliko katika fomu ya mteremko wa mstari.
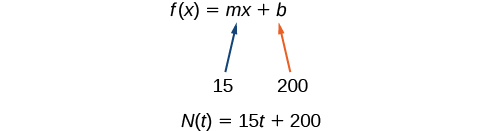
Tunaweza kuandika formula\(N(t)=15t+200\).
Kwa formula hii, tunaweza kutabiri ngapi nyimbo Marcus atakuwa na mwaka wa 1 (miezi 12). Kwa maneno mengine, tunaweza kutathmini kazi katika\(t=12\).
\[\begin{align*} N(12)&=15(12)+200 \\ &=180+200 \\ &= 380 \end{align*}\]
Marcus atakuwa na nyimbo 380 katika miezi 12.
Uchambuzi
Taarifa kwamba\(N\) ni kuongezeka linear kazi. Kadiri pembejeo (idadi ya miezi) inavyoongezeka, pato (idadi ya nyimbo) huongezeka pia.
Kufanya kazi kama mfanyabiashara wa bima, Ilya anapata mshahara wa msingi pamoja na tume ya kila sera mpya. Kwa hiyo, Ilya ya mapato ya kila wiki, I, inategemea idadi ya sera mpya\(n\), yeye anauza wakati wa wiki. Wiki iliyopita aliuza 3 sera mpya, na chuma $760 kwa wiki. Wiki moja kabla, aliuza sera mpya za 5 na kupata $920. Kupata equation kwa\(I(n)\), na kutafsiri maana ya vipengele vya equation.
Suluhisho
Taarifa iliyotolewa inatupa jozi mbili za pembejeo-pato:\((3,760)\) na\((5,920)\). Tunaanza kwa kutafuta kiwango cha mabadiliko.
\[\begin{align*} m&=\dfrac{920-760}{5-3} \\ &=\dfrac{$160}{2 \text{ policies}} \\ &=$80 \text{ per policy} \end{align*}\]
Kuweka wimbo wa vitengo inaweza kutusaidia kutafsiri kiasi hiki. Mapato yaliongezeka kwa $160 wakati idadi ya sera iliongezeka kwa 2, hivyo kiwango cha mabadiliko ni $80 kwa sera. Kwa hiyo, Ilya anapata tume ya $80 kwa kila sera kuuzwa wakati wa wiki.
Tunaweza kisha kutatua kwa thamani ya awali.
\[\begin{align*} I(n)&=80n+b \\ 760&=80(3)+b \text{ when } n=3, I(3)=760 \\ 760-80(3)&=b \\ 520 & =b \end{align*}\]
Thamani ya\(b\) ni thamani ya kuanzia kwa kazi na inawakilisha mapato ya Ilya wakati\(n=0\), au wakati hakuna sera mpya zinazouzwa. Tunaweza kutafsiri hili kama mshahara wa msingi wa Ilya kwa wiki, ambayo haitegemei idadi ya sera zinazouzwa.
Sasa tunaweza kuandika equation ya mwisho.
\[I(n)=80n+520 \nonumber\]
Tafsiri yetu ya mwisho ni kwamba mshahara wa msingi wa Ilya ni $520 kwa wiki na anapata tume ya ziada ya $80 kwa kila sera inayouzwa.
Equation kwa Kazi ya Linear
Jedwali\(\PageIndex{1}\) linahusiana na idadi ya panya katika idadi ya watu kwa wakati, katika wiki. Tumia meza kuandika equation linear.
| w, idadi ya wiki | 0 | 2 | 4 | 6 |
|---|---|---|---|---|
| P (w), idadi ya panya | 1000 | 1080 | 1160 | 1240 |
Suluhisho
Tunaweza kuona kutoka meza kwamba thamani ya awali kwa idadi ya panya ni 1000, hivyo\(b=1000\).
Badala ya kutatua\(m\), tunaweza kuwaambia kutokana na kuangalia meza kwamba idadi ya watu huongezeka kwa 80 kwa kila wiki 2 zinazopita. Hii ina maana kwamba kiwango cha mabadiliko ni panya 80 kwa wiki 2, ambayo inaweza kuwa rahisi kwa panya 40 kwa wiki.
\[P(w)=40w+1000 \nonumber\]
Ikiwa hatukuona kiwango cha mabadiliko kutoka meza, tunaweza bado kutatua kwa mteremko kwa kutumia pointi mbili kutoka meza. Kwa mfano, kwa kutumia\((2,1080)\) na\((6,1240)\)
\[\begin{align*} m&=\dfrac{1240-1080}{6-2} \\ &=\dfrac{160}{4} \\ &= 40\end{align*}\]
Je, thamani ya awali daima hutolewa katika meza ya maadili kama Jedwali\(\PageIndex{1}\)?
Hapana. Wakati mwingine thamani ya awali hutolewa katika meza ya maadili, lakini wakati mwingine sio. Ikiwa utaona pembejeo ya 0, basi thamani ya awali itakuwa pato linalofanana. Ikiwa thamani ya awali haitolewa kwa sababu hakuna thamani ya pembejeo kwenye meza sawa na 0, tafuta mteremko, ubadilishe jozi moja ya kuratibu na mteremko ndani\(f(x)=mx+b\), na utatua\(b\).
\(\PageIndex{5}\): Chakula kipya cha mmea kilianzishwa kwa mti mdogo ili kupima athari zake juu ya urefu wa mti. Jedwali\(\PageIndex{2}\) linaonyesha urefu wa mti, kwa miguu,\(x\) miezi tangu vipimo vilianza. Andika kazi linear\(H(x)\), ambapo\(x\) ni idadi ya miezi tangu kuanza kwa majaribio.
| \(x\) | 0 | 2 | 4 | 8 | 12 |
|---|---|---|---|---|---|
| \(H(x)\) | 12.5 | 13.5 | 14.5 | 16.5 | 18.5 |
Suluhisho
\(H(x)=0.5x+12.5\)
Mlinganyo muhimu
- aina ya mteremko wa mstari:\(f(x)=mx+b\)
- mteremko:\(m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\)
- aina ya mteremko wa mstari:\(y−y_1 =m(x-x_1)\)
Dhana muhimu
- Jozi zilizoamriwa zinazotolewa na kazi ya mstari zinawakilisha pointi kwenye mstari.
- Kazi za mstari zinaweza kuwakilishwa kwa maneno, alama ya kazi, fomu ya tabular, na fomu ya graphical.
- Kiwango cha mabadiliko ya kazi ya mstari pia inajulikana kama mteremko.
- Equation katika aina ya mteremko wa mstari ni pamoja na mteremko na thamani ya awali ya kazi.
- Thamani ya awali, au y-intercept, ni thamani ya pato wakati pembejeo ya kazi ya mstari ni sifuri. Ni thamani ya y ya hatua ambayo mstari unavuka mhimili wa y.
- Kuongezeka linear kazi matokeo katika grafu kwamba slants juu kutoka kushoto kwenda kulia na ina mteremko chanya.
- Kupungua linear kazi matokeo katika grafu kwamba slants chini kutoka kushoto kwenda kulia na ina mteremko hasi.
- Kazi ya mstari wa mara kwa mara husababisha grafu ambayo ni mstari usio na usawa.
- Kuchambua mteremko ndani ya muktadha wa tatizo unaonyesha kama kazi ya mstari inaongezeka, kupungua, au mara kwa mara.
- Mteremko wa kazi ya mstari unaweza kuhesabiwa kwa kugawanya tofauti kati ya maadili ya y kwa tofauti katika maadili ya x sawa ya pointi mbili kwenye mstari.
- Mteremko na thamani ya awali inaweza kuamua kupewa grafu au pointi mbili kwenye mstari.
- Aina moja ya uthibitisho wa kazi ni aina ya mteremko wa kuingilia kati ya equation.
- Fomu ya mteremko wa uhakika ni muhimu kwa kutafuta equation ya mstari wakati unapopewa mteremko wa mstari na hatua moja.
- Fomu ya mteremko wa uhakika pia ni rahisi kwa kupata equation ya mstari wakati inapewa pointi mbili ambazo mstari hupita.
- Ulinganisho wa kazi ya mstari unaweza kuandikwa ikiwa mteremko\(m\) na thamani ya awali\(b\) hujulikana.
- Kazi ya mstari inaweza kutumika kutatua matatizo halisi ya ulimwengu.
- Kazi ya mstari inaweza kuandikwa kutoka fomu ya tabular.
maelezo ya chini
1 www.chinahighlts.com/shang... glev-train.htm
2 www.cbsnews.com/8301-501465_1... ay-utafiti anasema/
faharasa
kupungua kwa kazi ya mstari
kazi na mteremko hasi: Kama\(f(x)=mx+b\), basi\(m<0\).
kuongeza kazi linear
kazi na mteremko chanya: Kama\(f(x)=mx+b\), basi\(m>0\).
kazi ya mstari
kazi na kiwango cha mara kwa mara cha mabadiliko ambayo ni polynomial ya shahada ya 1, na ambayo grafu ni mstari wa moja kwa moja
fomu ya mteremko
equation kwa mstari unaowakilisha kazi ya mstari wa fomu\ (y-y_1=m (x-x_1)
mteremko
uwiano wa mabadiliko katika maadili ya pato kwa mabadiliko katika maadili ya pembejeo; kipimo cha mwinuko wa mstari
fomu ya kupinga mteremko
equation kwa mstari unaowakilisha kazi linear katika fomu\(f(x)=mx+b\)
y-kukatiza
thamani ya kazi wakati thamani ya pembejeo ni sifuri; pia inajulikana kama thamani ya awali