1.E: Kazi (Mazoezi)

1.1: Kazi na Uthibitishaji wa Kazi

Jetliner inabadilisha urefu kama umbali wake kutoka mwanzo wa ndege huongezeka. Uzito wa mtoto anayekua huongezeka kwa wakati. Katika kila kesi, kiasi kimoja kinategemea mwingine. Kuna uhusiano kati ya kiasi mbili ambazo tunaweza kuelezea, kuchambua, na kutumia kufanya utabiri. Katika sehemu hii, tutachambua mahusiano hayo.

Maneno

1) ni tofauti kati ya uhusiano na kazi gani?

Jibu

Uhusiano ni seti ya jozi zilizoamriwa. Kazi ni aina maalum ya uhusiano ambayo hakuna jozi mbili zilizoamriwa zina kuratibu sawa kwanza.

2) Ni tofauti gani kati ya pembejeo na pato la kazi?

3) Kwa nini mtihani wa mstari wa wima unatuambia kama grafu ya uhusiano inawakilisha kazi?

Jibu

Wakati mstari wima intersects grafu ya uhusiano zaidi ya mara moja, kwamba inaonyesha kwamba kwa pembejeo kwamba kuna pato zaidi ya moja. Kwa thamani yoyote ya pembejeo, kunaweza kuwa na pato moja tu ikiwa uhusiano ni kuwa kazi.

4) Unawezaje kuamua kama uhusiano ni kazi moja kwa moja?

5) Kwa nini mtihani wa mstari wa usawa unatuambia kama grafu ya kazi ni moja kwa moja?

Jibu

Wakati mstari usawa intersects grafu ya kazi zaidi ya mara moja, kwamba inaonyesha kwamba kwa pato kwamba kuna pembejeo zaidi ya moja. Kazi ni moja kwa moja ikiwa kila pato linalingana na pembejeo moja tu.

Kialjebra

Kwa mazoezi 6-7, onyesha kama uhusiano unawakilisha kazi.

6)\(\{(a,b), (c,d), (a,c)\}\)

7)\(\{(a,b),(b,c),(c,c)\}\)

Jibu

kazi

Kwa mazoezi 8-26, kuamua kama uhusiano inawakilisha\(y\) kama kazi ya\(x\).

8)\(5x+2y=10\)

9)\(y=x^2\)

Jibu

kazi

10)\(x=y^2\)

11)\(3x^2+y=14\)

Jibu

kazi

12)\(2x+y^2=6\)

13)\(y=−2x^2+40x\)

Jibu

kazi

14)\(y=\dfrac{1}{x}\)

15)\(x=\dfrac{3y+5}{7y−1}\)

Jibu

kazi

16)\(x=\sqrt{1−y^2}\)

17)\(y=\dfrac{3x+5}{7x−1}\)

Jibu

kazi

18)\(x^2+y^2=9\)

19)\(2xy=1\)

Jibu

kazi

20)\(x=y^3\)

21)\(y=x^3\)

Jibu

kazi

22)\(y=\sqrt{1−x^2}\)

23)\(x=\pm\sqrt{1-y}\)

Jibu

kazi

24)\(y=\pm\sqrt{1−x}\)

25)\(y^2=x^2\)

Jibu

si kazi

26)\(y^3=x^2\)

Kwa mazoezi 27-39, tathmini kazi\(f\) katika maadili yaliyoonyeshwa\(f(−3),f(2),f(−a),−f(a),f(a+h)\).

27)\(f(x)=2x−5\)

Jibu

\(f(−3)=−11\);\(f(2)=−1\)\(f(−a)=−2a−5\);\(−f(a)=−2a+5\);\(f(a+h)=2a+2h−5\)

28)\(f(x)=−5x^2+2x−1\)

29)\(f(x)=\sqrt{2−x}+5\)

Jibu

\(f(−3)=\sqrt{5+5}\);\(f(2)=5\)\(f(−a)=\sqrt{2+a+5}\);\(−f(a)=−\sqrt{2−a}−5\);\(f(a+h)=\sqrt{2−a−h}+5\)

30)\(f(x)=\dfrac{6x−1}{5x+2}\)

31)\(f(x)=|x−1|−|x+1|\)

Jibu

\(f(−3)=2\);\(f(2)=1−3=−2\)\(f(−a)=|−a−1|−|−a+1|\);\(−f(a)=−|a−1| +|a+1|\);\(f(a+h)= |a+h−1|−|a+h+1|\)

32) Kutokana na kazi\(g(x)=5−x^2\), tathmini\(g(x+h)−g(x)h\),\(h{\neq}0\).

33) Kutokana na kazi\(g(x)=x^2+2x\), tathmini\(\dfrac{g(x)−g(a)}{x−a}\),\(x{\neq}a\).

Jibu

\(\dfrac{g(x)−g(a)}{x−a}=x+a+2\),\(x{\neq}a\)

34) Kutokana na kazi\(k(t)=2t−1\):

a. kutathmini\(k(2)\).
b. kutatua\(k(t)=7\).

35) Kutokana na kazi\(f(x)=8−3x\):

a. kutathmini\(f(−2)\).
b. kutatua\(f(x)=−1\).

Jibu

a.\(f(−2)=14\); b.\(x=3\)

36) Kutokana na kazi\(p(c)=c^2+c\):

a. kutathmini\(p(−3)\).
b. kutatua\(p(c)=2\).

37) Kutokana na kazi\(f(x)=x^2−3x\):

a. kutathmini\(f(5)\).
b. kutatua\(f(x)=4\).

Jibu

a.\(f(5)=10\); b.\(x=−1\) au\(x=4\)

38) Kutokana na kazi\(f(x)=\sqrt{x+2}\):

a. kutathmini\(f(7)\).
b. kutatua\(f(x)=4\).

39) Fikiria uhusiano\(3r+2t=18\).

Andika uhusiano kama kazi\(r=f(t)\).
b Tathmini\(f(−3)\).
c. kutatua\(f(t)=2\).

Jibu

a.\(f(t)=6−\frac{2}{3}t\); b.\(f(−3)=8\); c.\(t=6\)

Graphic

Kwa mazoezi 40-54, tumia mtihani wa mstari wa wima ili ueleze ambayo grafu zinaonyesha mahusiano ambayo ni kazi.

40)

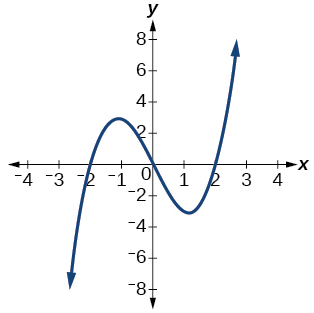
41)

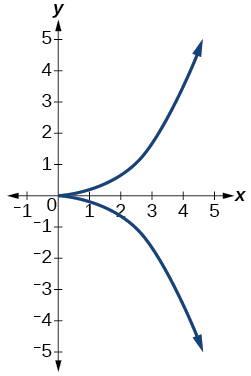
Jibu

si kazi

42)

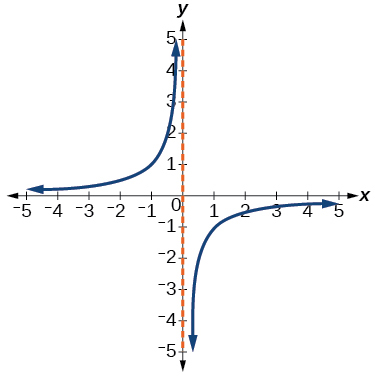
43)

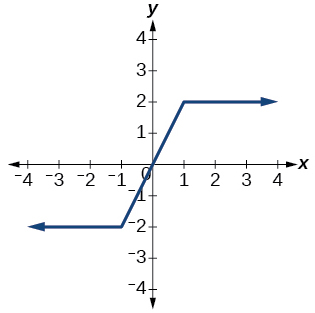
Jibu

kazi

44)

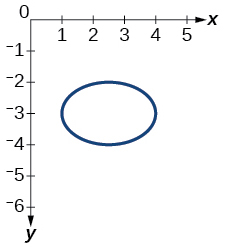
45)

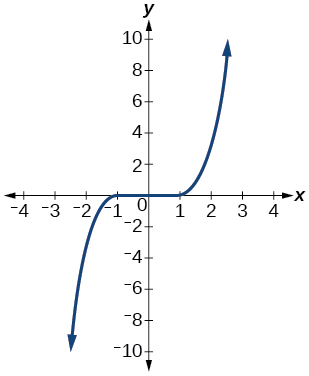
Jibu

kazi

46)

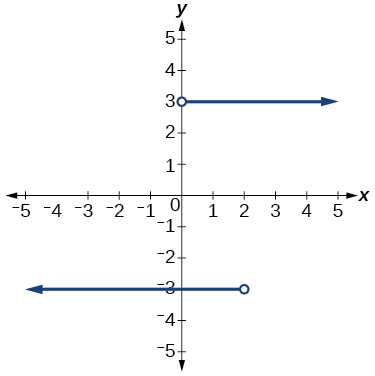
47)

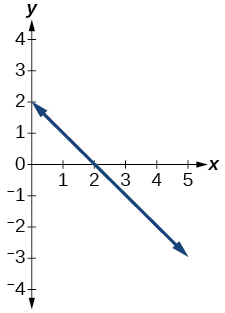
Jibu

kazi

48)

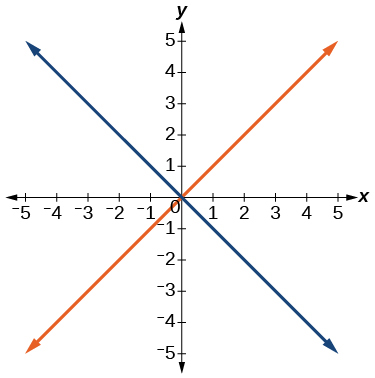
49)

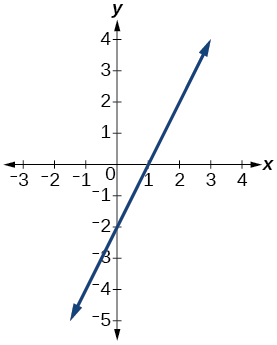
Jibu

kazi

50)

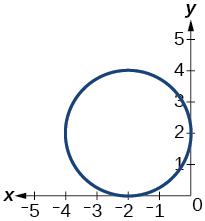
51)

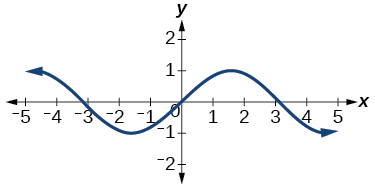
Jibu

kazi

52) Kutokana na grafu ifuatayo,

• Tathmini\(f(−1)\).
• Kutatua kwa\(f(x)=3\).

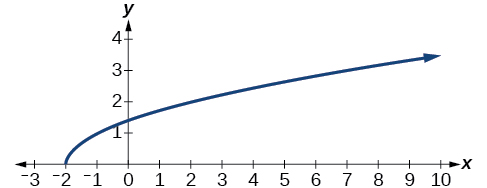
53) Kutokana na grafu ifuatayo,

• Tathmini\(f(0)\).
• Kutatua kwa\(f(x)=−3\).

Jibu

a.\(f(0)=1\); b.\(f(x)=−3\),\(x=−2\) au\(x=2\)

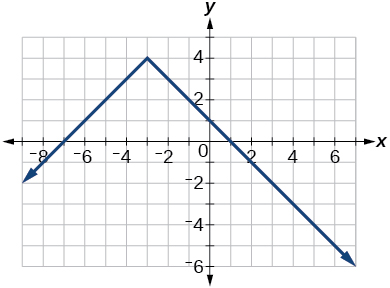
54) Kutokana na grafu ifuatayo,

• Tathmini\(f(4)\).
• Kutatua kwa\(f(x)=1\).

Kwa mazoezi 55-59, onyesha kama grafu iliyotolewa ni kazi moja kwa moja.

55)

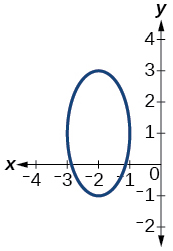
Jibu

si kazi hivyo pia si kazi moja kwa moja

56)

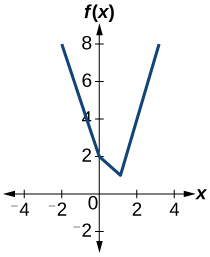
57)

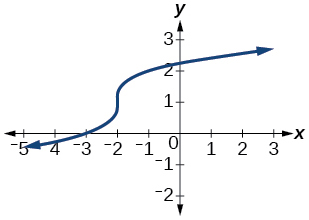
Jibu

kazi moja kwa moja

58)

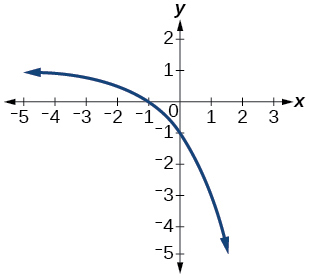
59)

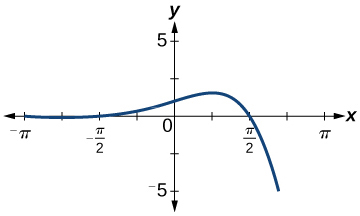
Jibu

kazi, lakini si moja kwa moja

Numeric

Kwa mazoezi 60-62, onyesha kama uhusiano unawakilisha kazi.

60)\(\{(−1,−1),(−2,−2),(−3,−3)\}\)

61)\(\{(3,4),(4,5),(5,6)\}\)

Jibu

kazi

62)\((2,5),(7,11),(15,8),(7,9)\}\)

Kwa ajili ya mazoezi 63-65, kuamua kama uhusiano kuwakilishwa katika fomu meza inawakilisha\(y\) kama kazi ya\(x\).

63)

\(x\)	5	10	15
\(y\)	3	8	14

Jibu

kazi

64)

\(x\)	5	10	15
\(y\)	3	8	8

65)

\(x\)	5	10	10
\(y\)	3	8	14

Jibu

si kazi

Kwa mazoezi 66-67, tumia kazi\(f\) iliyowakilishwa katika Jedwali hapa chini

\(x\)	\(f(x)\)
\ (x\) "> 0	\ (f (x)\) "> 74
\ (x\) ">1	\ (f (x)\) ">28
\ (x\) "> 2	\ (f (x)\) "> 1
\ (x\) ">3	\ (f (x)\) "> 53
\ (x\) ">4	\ (f (x)\) ">56
\ (x\) "> 5	\ (f (x)\) "> 3
\ (x\) ">6	\ (f (x)\) ">36
\ (x\) ">7	\ (f (x)\) "> 45
\ (x\) ">8	\ (f (x)\) ">14
\ (x\) ">9	\ (f (x)\) ">47

66) Tathmini\(f(3)\).

67) Tatua\(f(x)=1\).

Jibu

\(f(x)=1\),\(x=2\)

Kwa mazoezi 68-73, tathmini kazi\(f\) katika maadili\(f(−2)\),\(f(−1)\)\(f(0)\),\(f(1)\), na\(f(2)\).

68)\(f(x)=4−2x\)

69)\(f(x)=8−3x\)

Jibu

\(f(−2)=14\);\(f(−1)=11\)\(f(0)=8\);\(f(1)=5\);\(f(2)=2\)

70)\(f(x)=8x^2−7x+3\)

71)\(f(x)=3+\sqrt{x+3}\)

Jibu

\(f(−2)=4\);\(f(−1)=4.414\)\(f(0)=4.732\);\(f(1)=4.5\);\(f(2)=5.236\)

72)\(f(x)=\dfrac{x-2}{x+3}\)

73)\(f(x)=3^x\)

Jibu

\(f(−2)=\frac{1}{9}\);\(f(−1)=\frac{1}{3}\)\(f(0)=1\);\(f(1)=3\);\(f(2)=9\)

Kwa mazoezi 74-75, tathmini maneno, kazi zilizopewa\(f\)\(g\), na\(h\):

• \(f(x)=3x−2\)
• \(g(x)=5−x^2\)
• \(h(x)=−2x^2+3x−1\)

74)\(3f(1)−4g(−2)\)

75)\(f \left (\dfrac{7}{3} \right )−h(−2)\)

Jibu

\(20\)

Teknolojia

Kwa mazoezi 76-78, grafu\(y=x^2\) kwenye dirisha la kutazama. Tambua aina inayofanana kwa kila dirisha la kutazama. Onyesha kila grafu.

76)\([−0.1, 0.1]\)

77)\([−10, 10]\)

Jibu

\([0, 100]\)

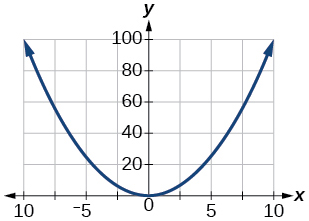
78)\([−100,100]\)

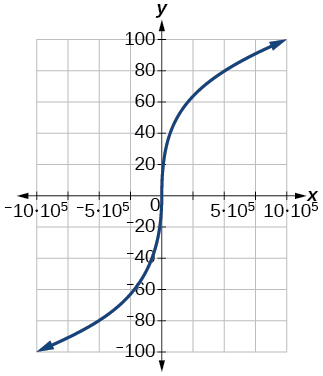
Kwa mazoezi 79-81, grafu\(y=x^3\) kwenye dirisha la kutazama. Tambua aina inayofanana kwa kila dirisha la kutazama. Onyesha kila grafu.

79)\([−0.1, 0.1]\)

Jibu

\([−0.001, 0.001]\)

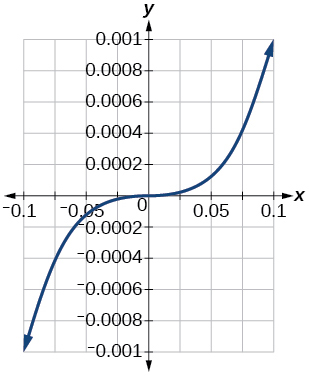
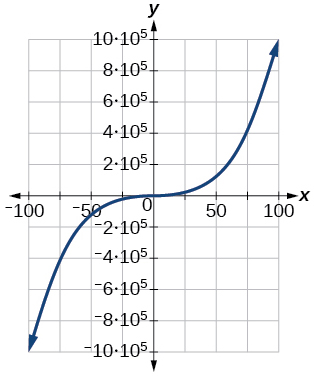
80)\([−10, 10]\)

81)\([−100, 100]\)

Jibu

\([−1,000,000, 1,000,000]\)

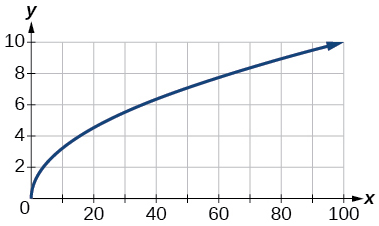
Kwa mazoezi 82-84, grafu\(y=\sqrt{x}\) kwenye dirisha la kutazama. Tambua aina inayofanana kwa kila dirisha la kutazama. Onyesha kila grafu.

82)\([0, 0.01]\)

83)\([0, 100]\)

Jibu

\([0, 10]\)

84)\([0, 10,000]\)

Kwa mazoezi 85-87, grafu\(y=\sqrt[3]{x}\) kwenye dirisha la kutazama. Tambua aina inayofanana kwa kila dirisha la kutazama. Onyesha kila grafu.

85)\([−0.001,0.001]\)

Jibu

\([−0.1,0.1]\)

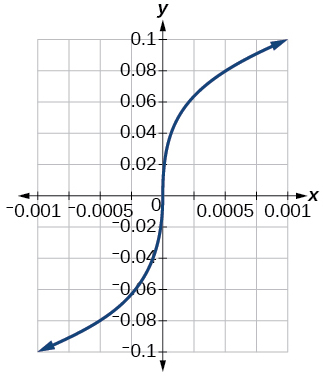
86)\([−1000,1000]\)

87)\([−1,000,000,1,000,000]\)

Jibu

\([−100, 100]\)

Real-World Matumizi

88) Kiasi cha takataka\(G\), zinazozalishwa na mji na idadi\(p\) ya watu hutolewa na\(G=f(p)\). \(G\)ni kipimo katika tani kwa wiki, na\(p\) ni kipimo katika maelfu ya watu.

Mji wa Tola una idadi ya watu\(40,000\) na hutoa\(13\) tani za takataka kila wiki. Express habari hii katika suala la kazi\(f\) .Tola ina idadi ya\(40,000\) na inazalisha\(13\) tani ya takataka kila wiki. Eleza habari hii kwa suala la kazi\(f\).
Eleza maana ya taarifa hiyo\(f(5)=2\).

89) Idadi ya yadi za ujazo za uchafu\(D\),, zinahitajika kufunika bustani na eneo la miguu ya mraba hutolewa na\(D=g(a)\).

a. bustani na eneo\(5000\)\(ft^2\) inahitaji\(50\)\(yd^3\) uchafu. Eleza habari hii kwa suala la kazi\(g\).
b Eleza maana ya taarifa hiyo\(g(100)=1\).

Jibu

a.\(g(5000)=50\); b. idadi ya yadi za ujazo wa uchafu inahitajika kwa ajili ya bustani ya miguu\(100\) mraba ni\(1\).

90) Hebu\(f(t)\) iwe idadi ya bata katika\(t\) miaka ya ziwa baada ya 1990. Eleza maana ya kila kauli:

a. f (5) =30
b. f (10) =40

91) Hebu\(h(t)\) kuwa urefu juu ya ardhi, katika miguu, ya roketi\(t\) sekunde baada ya uzinduzi. Eleza maana ya kila kauli:

a.\(h(1)=200\)
b.\(h(2)=350\)

Jibu

a. urefu wa roketi juu ya ardhi baada ya\(1\) pili ni\(200\) ft. b. urefu wa roketi juu ya ardhi baada ya\(2\) sekunde ni\(350\) ft.

92) Onyesha kwamba kazi\(f(x)=3(x−5)^2+7\) sio moja kwa moja.

1.2: Domain na Range

Katika kujenga kazi mbalimbali kwa kutumia data, tunaweza kutambua vigezo tofauti vya kujitegemea na vya tegemezi, na tunaweza kuchambua data na kazi za kuamua uwanja na upeo. Katika sehemu hii, tutachunguza mbinu za kuamua uwanja na kazi mbalimbali.

Maneno

1) Kwa nini uwanja hutofautiana kwa kazi tofauti?

Jibu

Kikoa cha kazi kinategemea maadili gani ya kutofautiana ya kujitegemea hufanya kazi isiyojulikana au ya kufikiri.

2) Tunawezaje kuamua uwanja wa kazi inayoelezwa na equation?

3) Eleza kwa nini uwanja wa\(f(x)=\sqrt[3]{x}\) ni tofauti na uwanja wa\(f(x)=\sqrt{x}\).

Jibu

Hakuna kizuizi juu ya x kwa\(f(x)=\sqrt[3]{x}\) sababu unaweza kuchukua mchemraba mizizi ya idadi yoyote halisi. Hivyo uwanja ni namba zote halisi,\((−∞,∞)\). Wakati wa kushughulika na seti ya namba halisi, huwezi kuchukua mizizi ya mraba ya namba hasi. Hivyo x-maadili ni vikwazo\(f(x)=\sqrt{x}\) kwa idadi nonnegative na uwanja ni\([0,∞)\).

4) Wakati wa kuelezea seti ya namba kwa kutumia nukuu ya muda, unatumia wakati gani mabano na unatumia bracket lini?

5) Je, wewe grafu kazi piecewise?

Jibu

Graph kila formula ya kazi piecewise juu ya uwanja wake sambamba. Tumia kiwango sawa kwa x-axis na y-axis kwa kila grafu. Eleza mwisho wa umoja na mduara imara na mwisho wa kipekee na mduara wazi. Tumia mshale kuonyesha\(−∞\) au\(∞\). Kuchanganya grafu ili kupata grafu ya kazi ya kipande.

Kialjebra

Kwa mazoezi 6-25, tafuta uwanja wa kila kazi ukitumia notation ya muda.

6)\(f(x)=−2x(x−1)(x−2)\)

7)\(f(x)=5−2x^2\)

Jibu

\((-\infty,\infty)\)

8)\(f(x)=3\sqrt{x-2}\)

9)\(f(x)=3-\sqrt{6-2x}\)

Jibu

\(\left(-\infty,3\right]\)

10)\(f(x)=\sqrt{4-3x}\)

11)\(f(x)=\sqrt{x^2+4}\)

Jibu

\((-\infty,\infty)\)

12)\(f(x)=\sqrt[3]{1-2x}\)

13)\(f(x)=\sqrt[3]{x-1}\)

Jibu

\((-\infty,\infty)\)

14)\(f(x)=\dfrac{9}{x-6}\)

15)\(f(x)=\dfrac{3x+1}{4x+2}\)

Jibu

\(\left (-\infty,-\dfrac{1}{2} \right )\cup \left (-\dfrac{1}{2},\infty \right )\)

16)\(f(x)=\dfrac{\sqrt{x+4}}{x-4}\)

17)\(f(x)=\dfrac{x-3}{x^2+9x-22}\)

Jibu

\((-\infty,-11)\cup(-11,2)\cup(2,\infty)\)

18)\(f(x)=\dfrac{1}{x^2-x-6}\)

19)\(f(x)=\dfrac{2x^3−250}{x^2−2x−15}\)

Jibu

\((-\infty,-3)\cup(-3,5)\cup(5,\infty)\)

20)\(\dfrac{5}{\sqrt{x-3}}\)

21)\(\dfrac{2x+1}{\sqrt{5-x}}\)

Jibu

\((-\infty,5)\)

22)\(\dfrac{\sqrt{x-4}}{\sqrt{x-6}}\)

23)\(\dfrac{\sqrt{x-6}}{\sqrt{x-4}}\)

Jibu

\(\left[6,\infty\right)\)

24)\(f(x)=\dfrac{x}{x}\)

25)\(f(x)=\dfrac{x^2-9x}{x^2-81}\)

Jibu

\((-\infty,-9)\cup(-9,9)\cup(9,\infty)\)

26) Pata uwanja wa kazi\(f(x)=\sqrt{2x^3-50x}\) na:

a. kutumia algebra

b. kuchora kazi katika radicna na kuamua vipindi kwenye x-axis ambayo radicand si negative.

Graphic

Kwa mazoezi 27-37, weka kikoa na upeo wa kila kazi kwa kutumia notation ya muda.

27)

\ (\ kushoto (2, 8\ haki]\).” style="background-rangi: uwazi; mpakana-chini-rangi: rgb (0, 0); mpaka chini-style: hakuna; mpaka chini-upana: 0px; mpaka picha-mwanzo: 0; mpako-picha-kurudia: kunyoosha; mpaka picha-kipande: 100%; mpaka picha-chanzo: hakuna; mpaka picha-upana: 1; mpaka-kushoto-rangi: rgb ( 0, 0, 0); mpaka-kushoto-style: hakuna; mpaka-kushoto-upana: 0px; mpaka-haki-rangi: rgb (0, 0, 0); mpaka-haki-style: hakuna; mpaka-haki-upana: 0px; mpaka-juu-rangi: rgb (0, 0, 0); mpaka-juu-style: hakuna; mpaka-juu-upana: 0px; rangi: rgb (0, 0, 0); mshale: default:; font-familia: lato, arial, helvetica, sans-serif, & quot; arial unicode ms “; font-size: 16px; font-style: kawaida; font-lahaja: kawaida; font-uzito: 400; urefu: 200px; barua-nafasi: kawaida; max-upana: 1224px; opacity: 0.8; yatima: 2; maandishi-align: kituo; maandishi mapambo: hakuna; Nakala-indent: 0px; Nakala-kubadilisha: hakuna; -webkit-text-upana wa kiharusi: 0px; nyeupe -nafasi: kawaida; upana: 200px; nafasi ya neno: 0px;” width="200px” height="200px” src=” https://math.libretexts.org/@api/dek..._01_02_202.jpg "/>

Jibu

kikoa:\(\left(2,8\right]\), mbalimbali\(\left[6,8\right)\)

28)

\ (\ kushoto [4, 8\ haki)\).” style="background-rangi: uwazi; mpakana-chini-rangi: rgb (0, 0); mpaka chini-style: hakuna; mpaka chini-upana: 0px; mpaka picha-mwanzo: 0; mpako-picha-kurudia: kunyoosha; mpaka picha-kipande: 100%; mpaka picha-chanzo: hakuna; mpaka picha-upana: 1; mpaka-kushoto-rangi: rgb ( 0, 0, 0); mpaka-kushoto-style: hakuna; mpaka-kushoto-upana: 0px; mpaka-haki-rangi: rgb (0, 0, 0); mpaka-haki-style: hakuna; mpaka-haki-upana: 0px; mpaka-juu-rangi: rgb (0, 0, 0); mpaka-juu-style: hakuna; mpaka-juu-upana: 0px; rangi: rgb (0, 0, 0); mshale: default:; font-familia: lato, arial, helvetica, sans-serif, & quot; arial unicode ms “; font-size: 16px; font-style: kawaida; font-lahaja: kawaida; font-uzito: 400; urefu: 200px; barua-nafasi: kawaida; max-upana: 1224px; opacity: 0.8; yatima: 2; maandishi-align: kituo; maandishi mapambo: hakuna; Nakala-indent: 0px; Nakala-kubadilisha: hakuna; -webkit-text-upana wa kiharusi: 0px; nyeupe -nafasi: kawaida; upana: 200px; nafasi ya neno: 0px;” width="200px” height="200px” src=” https://math.libretexts.org/@api/dek..._01_02_203.jpg "/>

29)

Jibu

kikoa:\([−4, 4]\), mbalimbali:\([0, 2]\)

30)

31)

Jibu

kikoa:\(\left[−5, 3\right)\), mbalimbali:\([0,2]\)

32)

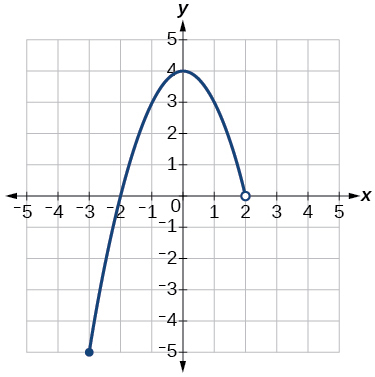
33)

Jibu

kikoa:\(\left(−\infty,1\right]\), mbalimbali:\(\left[0,\infty\right)\)

34)

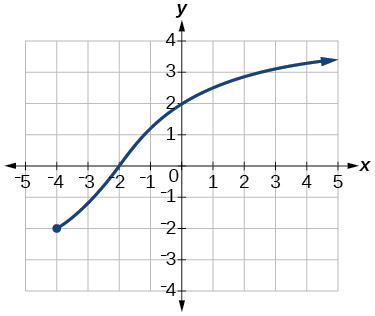
35)

Jibu

kikoa:\([−6,−16]\cup[16,6]\); mbalimbali:\([−6,−16]\cup[16,6]\)

36)

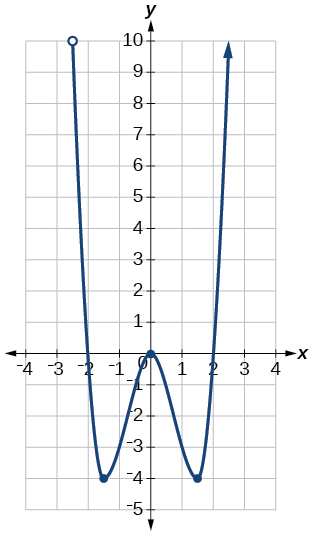
37)

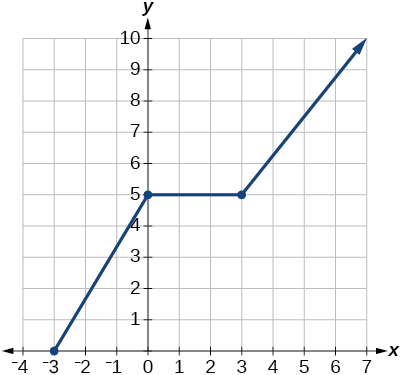
Jibu

kikoa:\(\left[−3, \infty\right)\); mbalimbali:\(\left[0,\infty\right)\)

Kwa mazoezi 38-45, mchoro grafu ya kazi ya kipande. Andika kikoa katika maelezo ya muda.

38)\(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\)

39)\(f(x)= \begin{cases} 2x-1 & \text{if $x < 1$} \\ 1+x & \text{if $x {\geq} 1$} \end{cases}\)

Jibu

kikoa:\((−\infty,\infty)\)

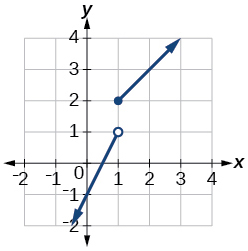
40)\(f(x)= \begin{cases} x+1 & \text{if $x < 0$} \\ x-1 & \text{if $x > 0$} \end{cases}\)

41)\(f(x)= \begin{cases} 3 & \text{if $x < 0$} \\ \sqrt{x} & \text{if $x {\geq} 0$} \end{cases}\)

Jibu

kikoa:\((−\infty,\infty)\)

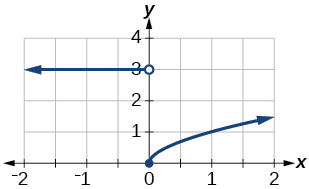
42)\(f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ 1-x & \text{if $x > 0$} \end{cases}\)

43)\(f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ x+2 & \text{if $x {\geq} 0$} \end{cases}\)

Jibu

kikoa:\((−\infty,\infty)\)

44)\(f(x)= \begin{cases} x+1 & \text{if $x < 1$} \\ x^3 & \text{if $x {\geq} 1$} \end{cases}\)

45)\(f(x)= \begin{cases} |x| & \text{if $x < 2$} \\ 1 & \text{if $x {\geq} 2$} \end{cases}\)

Jibu

kikoa:\((−\infty,\infty)\)

Numeric

Kwa mazoezi 46-48, kutokana na kila kazi\(f\), tathmini\(f(−3)\)\(f(−2)\),\(f(−1)\), na\(f(0)\).

46)\(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\)

47)\(f(x)= \begin{cases} 1 & \text{if $x \leq -3$} \\ 0 & \text{if $x > -3$} \end{cases}\)

Jibu

\(f(−3)=1\);\(f(−2)=0\);\(f(−1)=0\);\(f(0)=0\)

48)\(f(x)= \begin{cases} -2x^2+3 & \text{if $x \leq -1$} \\ 5x-7 & \text{if $x > -1$} \end{cases}\)

Kwa mazoezi 49-51, kutokana na kila kazi\(f\), tathmini\(f(−1)\),\(f(0)\),\(f(2)\), na\(f(4)\).

49)\(f(x)= \begin{cases} 7x+3 & \text{if $x < 0$} \\ 7x+6 & \text{if $x {\geq} 0$} \end{cases}\)

Jibu

\(f(−1)=−4\);\(f(0)=6\);\(f(2)=20\);\(f(4)=34\)

50)\(f(x)= \begin{cases} x^2-2 & \text{if $x < 2$} \\ 4+|x-5| & \text{if $x {\geq} 2$} \end{cases}\)

51)\(f(x)= \begin{cases} 5x & \text{if $x < 0$} \\ 3 & \text{if $0 {\geq} x {\leq} 2$} \\ x^2 & \text{if $x > 3$} \end{cases}\)

Jibu

\(f(−1)=−5\);\(f(0)=3\);\(f(2)=3\);\(f(4)=16\)

Kwa mazoezi ya 52-54, weka kikoa kwa kazi ya kipande katika notation ya muda.

52)\(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\)

53)\(f(x)= \begin{cases} x^2-2 & \text{if $x < 1$} \\ -x^2+2 & \text{if $x > 1$} \end{cases}\)

Jibu

kikoa:\((−\infty,1)\cup(1,\infty)\)

54)\(f(x)= \begin{cases} x^2-3 & \text{if $x < 0$} \\ -3x^2 & \text{if $x {\geq} 2$} \end{cases}\)

Teknolojia

55) Grafu\(y=\dfrac{1}{x^2}\) kwenye dirisha la kutazama\([−0.5,−0.1]\) na\([0.1,0.5]\). Tambua aina inayofanana kwa dirisha la kutazama. Onyesha grafu.

Jibu

dirisha:\([−0.5,−0.1]\); mbalimbali:\([4, 100]\)

dirisha:\([0.1, 0.5]\); mbalimbali:\([4, 100]\)

56) Grafu\(y=\dfrac{1}{x}\) kwenye dirisha la kutazama\([−0.5,−0.1]\) na\([0.1, 0.5]\). Tambua aina inayofanana kwa dirisha la kutazama. Onyesha grafu.

Ugani

57) Tuseme mbalimbali ya kazi\(f\) ni\([−5, 8]\). Je, ni aina gani ya\(|f(x)|\)?

Jibu

\([0, 8]\)

58) Unda kazi ambayo upeo ni namba zote zisizo za negative halisi.

59) Unda kazi ambayo uwanja ni\(x>2\).

Jibu

Majibu mengi. Kazi moja ni\(f(x)=\dfrac{1}{\sqrt{x-2}}\).

Real-World Matumizi

60) Urefu\(h\) wa projectile ni kazi ya wakati\(t\) ulio katika hewa. Urefu wa miguu kwa\(t\) sekunde hutolewa na kazi\(h(t)=−16t^2+96t\). Ni uwanja gani wa kazi? Je, kikoa kina maana gani katika mazingira ya tatizo?

Jibu

Domain ni\([0, 6]\); inachukua sekunde 6 kwa projectile kuondoka chini na kurudi chini

61) Gharama katika dola ya kufanya\(x\) vitu hutolewa na kazi\(C(x)=10x+500\).

a. gharama fasta ni kuamua wakati vitu sifuri ni zinazozalishwa. Pata gharama maalum ya kipengee hiki.

b Ni gharama gani ya kufanya\(25\) vitu?

c. tuseme gharama ya kiwango cha juu kuruhusiwa ni\(\$1500\). Je, ni uwanja na aina gani ya kazi ya gharama,\(C(x)\)?

1.3: Viwango vya Mabadiliko na Tabia ya Grafu

Katika sehemu hii, tutachunguza mabadiliko katika kazi. Kwa mfano, kiwango cha mabadiliko kinahusiana na mabadiliko katika wingi wa pato kwa mabadiliko katika wingi wa pembejeo. Kiwango cha wastani cha mabadiliko kinatambuliwa kutumia tu data ya mwanzo na ya mwisho. Kutambua pointi zinazoashiria muda kwenye grafu zinaweza kutumika kupata kiwango cha wastani cha mabadiliko. Kulinganisha jozi ya maadili ya pembejeo na pato katika meza pia inaweza kutumika kupata kiwango cha wastani cha mabadiliko.

Maneno

1) Je, kiwango cha wastani cha mabadiliko ya kazi kinaweza kuwa mara kwa mara?

Jibu

Ndiyo, kiwango cha wastani cha mabadiliko ya kazi zote za mstari ni mara kwa mara.

2) Ikiwa kazi\(f\) inaongezeka\((a,b)\) na kupungua\((b,c)\), basi ni nini kinachoweza kusema juu ya mwisho wa\(f\) ndani\((a,c)\)?

3) Je, kiwango cha juu kabisa na cha chini kinafanana na tofauti na extrema ya ndani?

Jibu

Upeo kabisa na kiwango cha chini kinahusiana na grafu nzima, wakati extrema ya ndani inahusiana tu na kanda maalum karibu na muda wa wazi.

4) Je, grafu ya kazi ya thamani kamili inalinganishaje na grafu ya kazi ya quadratic\(y=x^2\), kwa kuzingatia vipindi vya kuongezeka na kupungua?

Kialjebra

Kwa mazoezi 5-15, pata kiwango cha wastani cha mabadiliko ya kila kazi kwa muda uliowekwa kwa idadi halisi\(b\) au\(h\).

5)\(f(x)=4x^2−7\) juu\([1, b]\)

Jibu

\(4(b+1)\)

6)\(g(x)=2x^2−9\) juu\([4, b]\)

7)\(p(x)=3x+4\) juu\([2, 2+h]\)

Jibu

\(3\)

8)\(k(x)=4x−2\) juu\([3, 3+h]\)

9)\(f(x)=2x^2+1\) juu\([x,x+h]\)

Jibu

\(4x+2h\)

10)\(g(x)=3x^2−2\) juu\([x,x+h]\)

11)\(a(t)=\dfrac{1}{t+4}\) juu\([9,9+h]\)

Jibu

\(\dfrac{−1}{13(13+h)}\)

12)\(b(x)=1x+3\) juu\([1,1+h]\)

13)\(j(x)=3x^3\) juu\([1,1+h]\)

Jibu

\(3h^2+9h+9\)

14)\(r(t)=4t^3\) juu\([2,2+h]\)

15)\(\dfrac{f(x+h)−f(x)}{h}\)\(f(x)=2x^2−3x\) iliyotolewa\([x,x+h]\)

Jibu

\(4x+2h−3\)

Graphic

Kwa mazoezi 16-17, fikiria grafu ya\(f\) inavyoonekana kwenye Kielelezo hapa chini

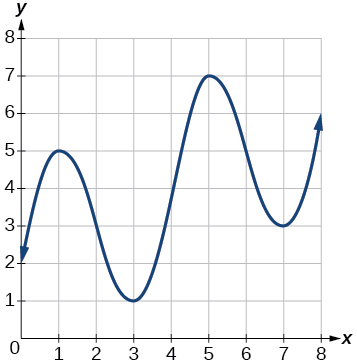
Grafu ya polynomial.

16) Tathmini ya kiwango cha wastani cha mabadiliko kutoka\(x=1\) kwa\(x=4\).

17) Tathmini ya kiwango cha wastani cha mabadiliko kutoka\(x=2\) kwa\(x=5\).

Jibu

\(\dfrac{4}{3}\)

Kwa mazoezi yafuatayo, tumia grafu ya kila kazi ili kukadiria vipindi ambavyo kazi inaongezeka au kupungua.

18)

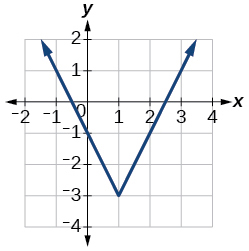
19)

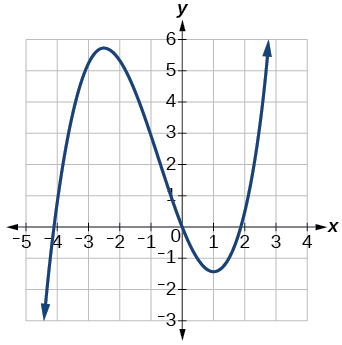
Jibu

kuongezeka\((−\infty,−2.5)\cup(1,\infty)\), kupungua\((−2.5, 1)\)

20)

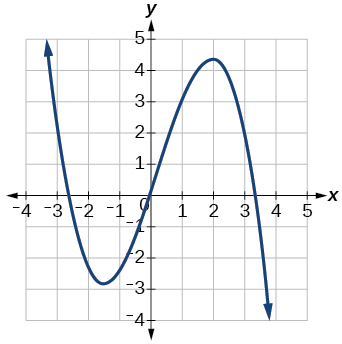
21)

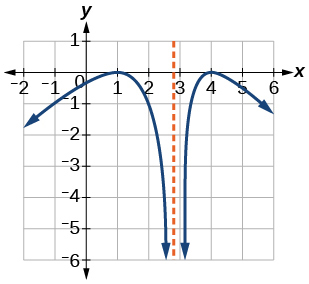
Jibu

kuongezeka\((−\infty,1)\cup(3,4)\), kupungua\((1,3)\cup(4,\infty)\)

Kwa mazoezi 22-23, fikiria grafu iliyoonyeshwa kwenye Kielelezo hapa chini.

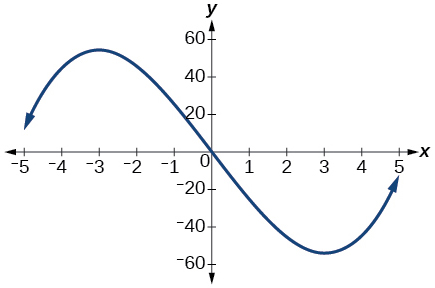
Grafu ya kazi ya ujazo.

22) Tathmini vipindi ambapo kazi inaongezeka au kupungua.

23) Tathmini hatua (s) ambayo grafu ya f ina upeo wa ndani au kiwango cha chini cha ndani.

Jibu

ndani ya kiwango cha juu:\((−3, 60)\), ndani ya kiwango cha chini:\((3, −60)\)

Kwa mazoezi 24-25, fikiria grafu katika Kielelezo hapa chini.

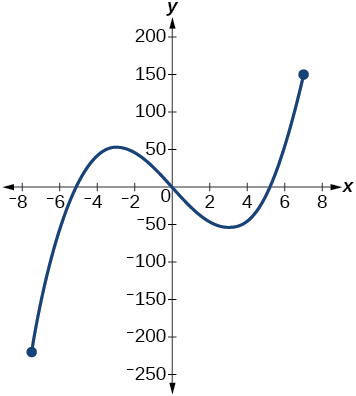
Grafu ya kazi ya ujazo.

24) Ikiwa grafu kamili ya kazi inavyoonyeshwa, tathmini vipindi ambapo kazi inaongezeka au kupungua.

25) Ikiwa grafu kamili ya kazi imeonyeshwa, tathmini kiwango cha juu kabisa na kiwango cha chini kabisa.

Jibu

upeo kabisa katika kiwango cha chini takriban\((7, 150)\), kabisa katika takriban\((−7.5, −220)\)

Numeric

26) Jedwali hapa chini linatoa mauzo ya kila mwaka (kwa mamilioni ya dola) ya bidhaa kutoka 1998 hadi 2006. Kiwango cha wastani cha mabadiliko ya mauzo ya kila mwaka (a) kati ya 2001 na 2002, na (b) kati ya 2001 na 2004?

Mwaka	Mauzo (mamilioni ya dola)
1998	201
1999	219
2000	233
2001	243
2002	249
2003	251
2004	249
2005	243
2006	233

27) Jedwali hapa chini linatoa idadi ya wakazi wa mji (kwa maelfu) kutoka 2000 hadi 2008. Kiwango cha wastani cha mabadiliko ya idadi ya watu (a) kati ya 2002 na 2004, na (b) kati ya 2002 na 2006?

Mwaka	Idadi ya watu (maelfu)
2000	87
2001	84
2002	83
2003	80
2004	77
2005	76
2006	78
2007	81
2008	85

Jibu

a.\(-3000\); b.\(-1250\)

Kwa mazoezi 28-34, pata kiwango cha wastani cha mabadiliko ya kila kazi kwa muda uliowekwa.

28)\(f(x)=x^2\) juu\([1, 5]\)

29)\(h(x)=5−2x^2\) juu\([−2,4]\)

Jibu

\(-4\)

30)\(q(x)=x^3\) juu\([−4,2]\)

31)\(g(x)=3x^3−1\) juu\([−3,3]\)

Jibu

\(27\)

32)\(y=\dfrac{1}{x}\) juu\([1, 3]\)

33)\(p(t)=\dfrac{(t^2-4)(t+1)}{t^2+3}\) juu\([-3,1]\)

Jibu

\(-0.167\)

34)\(k(t)=6t^2+\dfrac{4}{t^3}\) juu\([−1,3]\)

Teknolojia

Kwa mazoezi 35-40, tumia matumizi ya graphing ili kukadiria extrema ya ndani ya kila kazi na kukadiria vipindi ambavyo kazi inaongezeka na kupungua.

35)\(f(x)=x^4−4x^3+5\)

Jibu

Mitaa kima cha chini katika\((3,−22)\), kupungua juu ya\((−\infty, 3)\), kuongezeka kwa\((3, \infty)\)

36)\(h(x)=x^5+5x^4+10x^3+10x^2−1\)

37)\(g(t)=t\sqrt{t+3}\)

Jibu

Mitaa kima cha chini katika\((−2,−2)\), kupungua juu ya\((−3,−2)\), kuongezeka kwa\((−2, \infty)\)

38)\(k(t)=3t^{\frac{2}{3}}−t\)

39)\(m(x)=x^4+2x^3−12x^2−10x+4\)

Jibu

Mitaa ya kiwango cha juu katika\((−0.5, 6)\), minima mitaa katika\((−3.25,−47)\) na\((2.1,−32)\), kupungua juu\((−\infty,−3.25)\) na\((−0.5, 2.1)\), kuongeza juu\((−3.25, −0.5)\) na\((2.1,\infty)\)

40)\(n(x)=x^4−8x^3+18x^2−6x+2\)

Ugani

41) Grafu ya kazi\(f\) imeonyeshwa kwenye Kielelezo hapa chini:

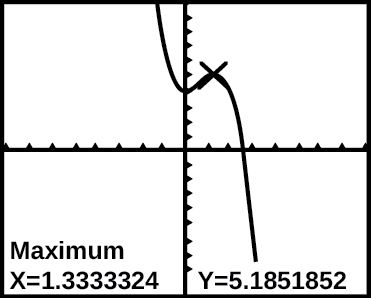
Grafu ya f (x) kwenye calculator ya graphing.

Kulingana na risasi ya skrini ya calculator, hatua\((1.333, 5.185)\) ni ipi ya yafuatayo?

1. upeo wa jamaa (wa ndani) wa kazi
2. vertex ya kazi
3. upeo kamili wa kazi
4. sifuri ya kazi

Jibu

a

42) Hebu\(f(x)=\dfrac{1}{x}\). Pata idadi\(c\) kama vile kiwango cha wastani cha mabadiliko ya kazi f kwenye muda\((1,c)\) ni\(-\dfrac{1}{4}\).

43) Hebu\(f(x)=\dfrac{1}{x}\). Kupata idadi\(b\) kama kwamba kiwango cha wastani wa mabadiliko ya f juu ya muda\((2,b)\) ni\(−\dfrac{1}{10}\).

Jibu

\(b=5\)

Real-World Matumizi

44) Mwanzoni mwa safari, odometer kwenye gari inasoma\(21,395\). Mwishoni mwa safari,\(13.5\) masaa baadaye, odometer inasoma\(22,125\). Tuseme kiwango kwenye odometer iko katika maili. Je, ni wastani wa kasi gari lililotembea wakati wa safari hii?

45) Dereva wa gari alisimama kwenye kituo cha gesi ili kujaza tank yake ya gesi. Aliangalia saa yake, na wakati ulisoma hasa 3:40 p.m. Kwa wakati huu, alianza kusukwa gesi ndani ya tangi. Saa 3:44, tangi ilikuwa imejaa na aliona kwamba alikuwa amepiga\(10.7\) galoni. Kiwango cha wastani cha mtiririko wa petroli ndani ya tank ya gesi ni nini?

Jibu

\(2.7\)galoni kwa dakika

46) Karibu na uso wa mwezi, umbali ambao kitu kinaanguka ni kazi ya wakati. Inatolewa na\(d(t)=2.6667t^2\), wapi\(t\) sekunde na\(d(t)\) iko katika miguu. Ikiwa kitu kimeshuka kutoka urefu fulani, pata kasi ya wastani ya kitu kutoka\(t=1\) kwa\(t=2\).

47) Grafu katika Kielelezo hapa chini inaonyesha kuoza kwa dutu ya mionzi zaidi ya\(t\) siku.

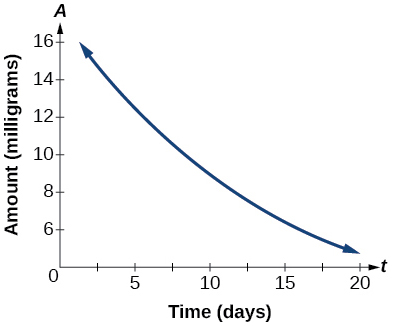
Grafu ya kazi ya kielelezo.

Tumia grafu ili kukadiria kiwango cha wastani cha kuoza kutoka\(t=5\) hadi\(t=15\).

Jibu

takriban\(-0.6\) miligramu kwa siku

1.4: Muundo wa Kazi

Tuseme tunataka kuhesabu ni kiasi gani kinachohitajika kwa joto la nyumba siku fulani ya mwaka. Gharama ya joto nyumba itategemea wastani wa joto la kila siku, na kwa upande mwingine, wastani wa joto la kila siku hutegemea siku fulani ya mwaka. Gharama inategemea joto, na joto hutegemea siku. Kwa kuchanganya mahusiano haya mawili katika kazi moja, tumefanya utungaji wa kazi, ambayo ni lengo la sehemu hii.

Maneno

1) Je, mtu hupataaje uwanja wa quotient ya kazi mbili,\(\dfrac{f}{g}\)?

Jibu

Pata namba zinazofanya kazi katika denominator\(g\) sawa na sifuri, na uangalie vikwazo vingine vya kikoa\(f\) na\(g\), kama vile mzizi wa hata-indexed au zero katika denominator.

2) Ni muundo gani wa kazi mbili,\(f{\circ}g\)?

3) Ikiwa utaratibu umebadilishwa wakati wa kutengeneza kazi mbili, je, matokeo yanaweza kuwa sawa na jibu katika utaratibu wa awali wa muundo? Ikiwa ndiyo, fanya mfano. Kama hapana, kueleza kwa nini si.

Jibu

Ndiyo. Jibu la sampuli: Hebu\(f(x)=x+1\) na\(g(x)=x−1\). Kisha\(f(g(x))=f(x−1)=(x−1)+1=x\) na\(g(f(x))=g(x+1)=(x+1)−1=x\). Hivyo\(f{\circ}g=g{\circ}f\).

4) Je, unapataaje kikoa cha utungaji wa kazi mbili,\(f{\circ}g\)?

Kialjebra

5) Kutokana\(f(x)=x^2+2x\) na\(g(x)=6−x^2\), tafuta\(f+g\),\(f−g\)\(fg\), na\(\dfrac{f}{g}\) .Tambua kikoa kwa kila kazi katika notation ya muda.

Jibu

\((f+g)(x)=2x+6\), kikoa:\((−\infty,\infty)\)

\((f−g)(x)=2x^2+2x−6\), kikoa:\((−\infty,\infty)\)

\((fg)(x)=−x^4−2x^3+6x^2+12x\), kikoa:\((−\infty,\infty)\)

\(\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2+2x}{6−x^2},\)kikoa:\( (−\infty,−\sqrt{6})\cup(\sqrt{6},\sqrt{6})\cup(\sqrt{6},\infty)\)

6) Kutokana\(f(x)=−3x^2+x\) na\(g(x)=5\), kupata\(f+g\),\(f−g\),\(fg\), na\(\dfrac{f}{g}\). Tambua kikoa kwa kila kazi katika notation ya muda.

7) Kutokana\(f(x)=2x^2+4x\) na\(g(x)=\dfrac{1}{2x}\), kupata\(f+g\),\(f−g\),\(fg\), na\(\dfrac{f}{g}\). Tambua kikoa kwa kila kazi katika notation ya muda.

Jibu

\((f+g)(x)=\dfrac{4x^3+8x^2+1}{2x}\), kikoa:\((−\infty,0)\cup(0,\infty)\)

\((f−g)(x)=\dfrac{4x3+8x2−1}{2x}\), kikoa:\((−\infty,0)\cup(0,\infty)\)

\((fg)(x)=x+2\), kikoa:\((−\infty,0)\cup(0,\infty)\)

\((fg)(x)=4x^3+8x^2\), kikoa:\((−\infty,0)\cup(0,\infty)\)

8) Kutokana\(f(x)=\dfrac{1}{x−4}\) na\(g(x)=\dfrac{1}{6−x}\), kupata\(f+g\),\(f−g\),\(fg\), na\(\dfrac{f}{g}\). Tambua kikoa kwa kila kazi katika notation ya muda.

9) Kutokana\(f(x)=3x^2\) na\(g(x)=\sqrt{x−5}\), kupata\(f+g\),\(f−g\),\(fg\), na\(\dfrac{f}{g}\). Tambua kikoa kwa kila kazi katika notation ya muda.

Jibu

\((f+g)(x)=3x^2+\sqrt{x−5}\), kikoa:\(\left[5,\infty\right)\)

\((f−g)(x)=3x^2−\sqrt{x−5}\), kikoa:\(\left[5,\infty\right)\)

\((fg)(x)=3x^2\sqrt{x−5}\), kikoa:\(\left[5,\infty\right)\)

\(\left(\dfrac{f}{g}\right)(x)=\dfrac{3x^2}{\sqrt{x−5}}\), kikoa:\((5,\infty)\)

10) Kutokana\(f(x)=\sqrt{x}\) na\(g(x)=|x−3|\), kupata\(\dfrac{g}{f}\). Tambua kikoa cha kazi katika maelezo ya muda.

11) Kutokana\(f(x)=2x^2+1\) na\(g(x)=3x−5\), kupata zifuatazo:

1. \(f(g(2))\)
2. \(f(g(x))\)
3. \(g(f(x))\)
4. \((g{\circ}g)(x)\)
5. \((f{\circ}f)(−2)\)

Jibu

1. \(3\)
2. \(f(g(x))=2(3x−5)^2+1\)
3. \(f(g(x))=6x^2−2\)
4. \((g{\circ}g)(x)=3(3x−5)−5=9x−20\)
5. \((f{\circ}f)(−2)=163\)

Kwa mazoezi 12-17, tumia kila jozi ya kazi ili kupata\(f(g(x))\) na\(g(f(x))\). Kurahisisha majibu yako.

12)\(f(x)=x^2+1\),\(g(x)=\sqrt{x+2}\)

13)\(f(x)=\sqrt{x}+2\),\(g(x)=x^2+3\)

Jibu

\(f(g(x))=\sqrt{x+3}\),\(g(f(x))=x+4\sqrt{x}+7\)

14)\(f(x)=|x|\),\(g(x)=5x+1\)

15)\(f(x)=\sqrt[3]{x}\),\(g(x)=\dfrac{x+1}{x^3}\)

Jibu

\(f(g(x))=\sqrt[3]{\dfrac{x+1}{x^3}}=\dfrac{\sqrt[3]{x+1}}{x}\),\(g(f(x))=\dfrac{\sqrt[3]{x}+1}{x}\)

16)\(f(x)=\dfrac{1}{x−6}\),\(g(x)=\dfrac{7}{x}+6\)

17)\(f(x)=\dfrac{1}{x−4}\),\(g(x)=\dfrac{2}{x}+4\)

Jibu

\((f{\circ}g)(x)=\dfrac{1}{\frac{2}{x}+4-4}=\dfrac{x}{2}\),\((g{\circ}f)(x)=2x-4\)

Kwa mazoezi 18-25, tumia kila seti ya kazi ili kupata f (g (h (x))). Kurahisisha majibu yako.

18)\(f(x)=x^4+6\),\(g(x)=x−6\), na\(h(x)=\sqrt{x}\)

19)\(f(x)=x^2+1\),\(g(x)=\dfrac{1}{x}\), na\(h(x)=x+3\)

Jibu

\(f(g(h(x)))=\left(\dfrac{1}{x+3}\right)^2+1\)

20) Kutokana\(f(x)=\dfrac{1}{x}\) na\(g(x)=x−3\), kupata zifuatazo:

1. \((f{\circ}g)(x)\)
2. uwanja wa\((f{\circ}g)(x)\) notation ya muda
3. \((g{\circ}f)(x)\)
4. uwanja wa\((g{\circ}f)(x)\)
5. \(\left(\dfrac{f}{g}\right)x\)

21) Kutokana\(f(x)=\sqrt{2−4x}\) na\(g(x)=−\dfrac{3}{x}\), kupata zifuatazo:

1. \((g{\circ}f)(x)\)
2. uwanja wa\((g{\circ}f)(x)\) notation ya muda

Jibu

1. \((g{\circ}f)(x)=−\dfrac{3}{\sqrt{2−4x}}\)
2. \(\left(−\infty,\dfrac{1}{2}\right)\)

22) Kutokana na kazi\(f(x)=\dfrac{1−x}{x}\) na\(g(x)=\dfrac{1}{1+x^2}\), kupata zifuatazo:

1. \((g{\circ}f)(x)\)
2. \((g{\circ}f)(2)\)

23) Kutokana\(p(x)=\dfrac{1}{\sqrt{x}}\) na kazi na\(m(x)=x^2−4\), hali ya uwanja wa kila moja ya kazi zifuatazo kwa kutumia muda notation:

1. \(\dfrac{p(x)}{m(x)}\)
2. \(p(m(x))\)
3. \(m(p(x))\)

Jibu

1. \((0,2)\cup(2,\infty)\)
2. \((−\infty,−2)\cup(2,\infty)\)
3. \((0,\infty)\)

24) Kutokana\(q(x)=\dfrac{1}{\sqrt{x}}\) na kazi na\(h(x)=x^2−9\), hali ya uwanja wa kila moja ya kazi zifuatazo kwa kutumia muda notation.

1. \(\dfrac{q(x)}{h(x)}\)
2. \(q(h(x))\)
3. \(h(q(x))\)

25) Kwa\(f(x)=\dfrac{1}{x}\) na\(g(x)=\sqrt{x−1}\), kuandika uwanja wa\((f{\circ}g)(x)\) katika nukuu ya muda.

Jibu

\((1,\infty)\)

Kwa mazoezi 26-41, kupata kazi\(f(x)\) na\(g(x)\) hivyo kazi iliyotolewa inaweza kuelezwa kama\(h(x)=f(g(x))\).

26)\(h(x)=(x+2)^2\)

27)\(h(x)=(x−5)^3\)

Jibu

sampuli:\(f(x)=x^3\)

\(g(x)=x−5\)

28)\(h(x)=\dfrac{3}{x−5}\)

29)\(h(x)=\dfrac{4}{(x+2)^2}\)

Jibu

sampuli:\(f(x)=\dfrac{4}{x}\)

\(g(x)=(x+2)^2\)

30)\(h(x)=4+\sqrt[3]{x}\)

31)\(h(x)=\sqrt[3]{\dfrac{1}{2x−3}}\)

Jibu

sampuli:\(f(x)=\sqrt[3]{x}\)

\(g(x)=\dfrac{1}{2x−3}\)

32)\(h(x)=\dfrac{1}{(3x^2−4)^{−3}}\)

33)\(h(x)=\sqrt[4]{\dfrac{3x−2}{x+5}}\)

Jibu

sampuli:\(f(x)=\sqrt[4]{x}\)

\(g(x)=\dfrac{3x−2}{x+5}\)

34)\(h(x)=(\dfrac{8+x^3}{8−x^3})^4\)

35)\(h(x)=\sqrt{2x+6}\)

Jibu

sampuli:\(f(x)=\sqrt{x}\)

\(g(x)=2x+6\)

36)\(h(x)=(5x−1)^3\)

37)\(h(x)=\sqrt[3]{x−1}\)

Jibu

sampuli:\(f(x)=\sqrt[3]{x}\)
\(g(x)=(x−1)\)

38)\(h(x)=|x^2+7|\)

39)\(h(x)=\dfrac{1}{(x−2)^3}\)

Jibu

sampuli:\(f(x)=x^3\)
\(g(x)=\dfrac{1}{x−2}\)

40)\(h(x)=\left(\dfrac{1}{2x−3}\right)^2\)

41)\(h(x)=\sqrt { \dfrac{2x−1}{3x+4}}\)

Jibu

sampuli:\(f(x)=\sqrt{x}\)
\(g(x)=\dfrac{2x−1}{3x+4}\)

Graphic

Kwa ajili ya mazoezi 42-49, kutumia grafu ya\(f\), inavyoonekana katika Kielelezo 1, na\(g\), inavyoonekana katika Kielelezo 2, kutathmini maneno.

Kielelezo 1: Grafu ya kazi.

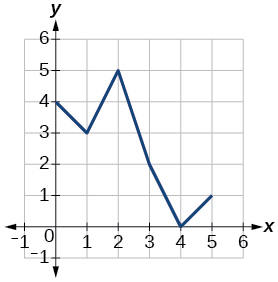
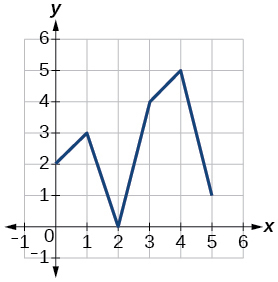
Kielelezo 2: Grafu ya kazi.

42)\(f(g(3))\)

43)\(f(g(1))\)

Jibu

\(2\)

44)\(g(f(1))\)

45)\(g(f(0))\)

Jibu

\(5\)

46)\(f(f(5))\)

47)\(f(f(4))\)

Jibu

\(4\)

48)\(g(g(2))\)

49)\(g(g(0))\)

Jibu

\(0\)

Kwa ajili ya mazoezi 50-57, kutumia grafu ya\(f(x)\), inavyoonekana katika Kielelezo 3\(g(x)\), inavyoonekana katika Kielelezo 4, na\(h(x)\), inavyoonekana katika Kielelezo 5, kutathmini maneno.

Kielelezo 3: Grafu ya parabola.

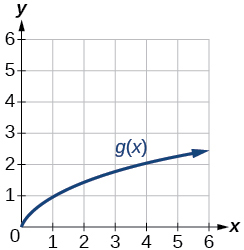
Kielelezo 4: Grafu ya kazi ya mizizi ya mraba.

Kielelezo 5: Grafu ya kazi kamili ya thamani.

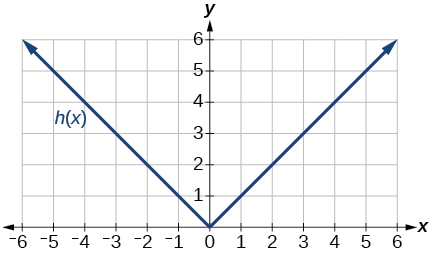
50)\(g(f(1))\)

51)\(g(f(2))\)

Jibu

\(2\)

52)\(f(g(4))\)

53)\(f(g(1))\)

Jibu

\(1\)

54)\(f(h(2))\)

55)\(h(f(2))\)

Jibu

\(4\)

56)\(f(g(h(4)))\)

57)\(f(g(f(−2)))\)

Jibu

\(4\)

Numeric

Kwa mazoezi 58-65, tumia maadili ya kazi\(f\) na\(g\) umeonyeshwa katika Jedwali hapa chini ili kutathmini kila kujieleza.

\(x\)	\(f(x)\)	\(g(x)\)
\ (x\) "> 0	\ (f (x)\) "> 7	\ (g (x)\) "> 9
\ (x\) ">1	\ (f (x)\) "> 6	\ (g (x)\) "> 5
\ (x\) "> 2	\ (f (x)\) "> 5	\ (g (x)\) "> 6
\ (x\) ">3	\ (f (x)\) "> 8	\ (g (x)\) "> 2
\ (x\) ">4	\ (f (x)\) "> 4	\ (g (x)\) "> 1
\ (x\) "> 5	\ (f (x)\) "> 0	\ (g (x)\) "> 8
\ (x\) ">6	\ (f (x)\) "> 2	\ (g (x)\) ">7
\ (x\) ">7	\ (f (x)\) "> 1	\ (g (x)\) "> 3
\ (x\) ">8	\ (f (x)\) "> 9	\ (g (x)\) "> 4
\ (x\) ">9	\ (f (x)\) "> 3	\ (g (x)\) "> 0

58)\(f(g(8))\)

59)\(f(g(5))\)

Jibu

\(9\)

60)\(g(f(5))\)

61)\(g(f(3))\)

Jibu

\(4\)

62)\(f(f(4))\)

63)\(f(f(1))\)

Jibu

\(2\)

64)\(g(g(2))\)

65)\(g(g(6))\)

Jibu

\(3\)

Kwa mazoezi 66-71, tumia maadili ya kazi\(f\) na\(g\) umeonyeshwa katika Jedwali hapa chini ili kutathmini maneno.

\(x\)	\(f(x)\)	\(g(x)\)
\ (x\) ">-3	\ (f (x)\) "> 11	\ (g (x)\) ">-8
\ (x\) ">-2	\ (f (x)\) "> 9	\ (g (x)\) ">-3
\ (x\) ">-1	\ (f (x)\) "> 7	\ (g (x)\) "> 0
\ (x\) "> 0	\ (f (x)\) "> 5	\ (g (x)\) "> 1
\ (x\) ">1	\ (f (x)\) "> 3	\ (g (x)\) "> 0
\ (x\) "> 2	\ (f (x)\) "> 1	\ (g (x)\) ">-3
\ (x\) ">3	\ (f (x)\) ">-1	\ (g (x)\) ">-8

66)\((f{\circ}g)(1)\)

67)\((f{\circ}g)(2)\)

Jibu

\(11\)

68)\((g{\circ}f)(2)\)

69)\((g{\circ}f)(3)\)

Jibu

\(0\)

70)\((g{\circ}g)(1)\)

71)\((f{\circ}f)(3)\)

Jibu

\(7\)

Kwa mazoezi 72-75, tumia kila jozi ya kazi ili kupata\(f(g(0))\) na\(g(f(0))\).

72)\(f(x)=4x+8\),\(g(x)=7−x^2\)

73)\(f(x)=5x+7\),\(g(x)=4−2x^2\)

Jibu

\(f(g(0))=27\),\(g(f(0))=−94\)

74)\(f(x)=\sqrt{x+4}\),\(g(x)=12−x^3\)

75)\(f(x)=\frac{1}{x+2}\),\(g(x)=4x+3\)

Jibu

\(f(g(0))=\frac{1}{5}\),\(g(f(0))=5\)

Kwa mazoezi 76-79, tumia kazi\(f(x)=2x^2+1\) na\(g(x)=3x+5\) kutathmini au kupata kazi ya composite kama ilivyoonyeshwa.

76)\(f(g(2))\)

77)\(f(g(x))\)

Jibu

\(18x^2+60x+51\)

78)\(g(f(−3))\)

79)\((g{\circ}g)(x)\)

Jibu

\(g{\circ}g(x)=9x+20\)

Upanuzi

Kwa mazoezi 80-84, tumia\(f(x)=x^3+1\) na\(g(x)=\sqrt[3]{x−1}\).

80) Kupata\((f{\circ}g)(x)\) na\((g{\circ}f)(x)\). Linganisha majibu mawili.

81) Kupata\((f{\circ}g)(2)\) na\((g{\circ}f)(2)\).

Jibu

\(2\)

82) Ni uwanja wa\((g{\circ}f)(x)\) nini?

83) Ni uwanja wa\((f{\circ}g)(x)\) nini?

Jibu

\((−\infty,\infty)\)

84) Hebu\(f(x)=\frac{1}{x}\).

1. Kupata\((f{\circ}f)(x)\).
2. Ni\((f{\circ}f)(x)\) kwa ajili\(f\) ya kazi yoyote matokeo sawa na jibu kwa sehemu (a) kwa ajili ya kazi yoyote? Eleza.

Kwa mazoezi 85-87, basi\(F(x)=(x+1)^5\),\(f(x)=x^5\), na\(g(x)=x+1\).

85) Kweli au Uongo:\((g{\circ}f)(x)=F(x)\).

Jibu

Uongo

86) Kweli au Uongo:\((f{\circ}g)(x)=F(x)\).

Kwa mazoezi 87-89, pata utungaji wakati\(f(x)=x^2+2\) wa wote\(x\geq0\) na\(g(x)=\sqrt{x−2}\).

87)\((f{\circ}g)(6)\);\((g{\circ}f)(6)\)

Jibu

\((f{\circ}g)(6)=6\);\((g{\circ}f)(6)=6\)

88)\((g{\circ}f)(a)\);\((f{\circ}g)(a)\)

89)\((f{\circ}g)(11)\);\((g{\circ}f)(11)\)

Jibu

\((f{\circ}g)(11)=11\),\((g{\circ}f)(11)=11\)

Real-World Matumizi

90) Kazi\(D(p)\) inatoa idadi ya vitu ambayo itahitajika wakati bei ni\(p\). Gharama ya uzalishaji\(C(x)\) ni gharama ya kuzalisha\(x\) vitu. Kuamua gharama za uzalishaji wakati bei ni\(\$6\), ungependa kufanya ni ipi ya yafuatayo?

1. Tathmini\(D(C(6))\)
2. Tathmini\(C(D(6))\)
3. Kutatua\(D(C(x))=6\)
4. Kutatua\(C(D(p))=6\)

91) Kazi\(A(d)\) hutoa kiwango cha maumivu kwa kiwango cha\(10\) uzoefu na mgonjwa mwenye\(d\) milligrams ya madawa ya kulevya ya kupunguza maumivu katika mfumo wake.\(0\) Miligramu ya madawa ya kulevya katika mfumo wa mgonjwa baada ya\(t\) dakika inaelekezwa na\(m(t)\). Ni ipi kati ya yafuatayo ungefanya ili kuamua wakati mgonjwa atakuwa katika kiwango cha maumivu ya\(4\)?

1. Tathmini\(A(m(4))\)
2. Tathmini\(m(A(4))\)
3. Kutatua\(A(m(t))=4\)
4. Kutatua\(m(A(d))=4\)

Jibu

c

92) Duka inatoa wateja\(30\%\) discount juu ya bei\(x\) ya vitu kuchaguliwa. Kisha, duka huchukua ziada\(15\%\) kwenye rekodi ya fedha. Andika kazi ya bei\(P(x)\) inayohesabu bei ya mwisho ya kipengee kulingana na bei ya awali\(x\). (Kidokezo: Tumia utungaji wa kazi ili kupata jibu lako.)

93) Kushuka kwa mvua kupiga ziwa hufanya kupasuka kwa mviringo. Ikiwa radius, kwa inchi, inakua kama kazi ya muda kwa dakika kulingana na\(r(t)=25\sqrt{t+2}\), tafuta eneo la kupigwa kama kazi ya wakati. Kupata eneo la ripple katika\(t=2\).

Jibu

\(A(t)=\pi(25\sqrt{t+2})^2\)na inchi\(A(2)=\pi(25\sqrt{4})^2=2500\pi\) za mraba

94) Moto wa misitu huacha nyuma ya eneo la nyasi lililochomwa moto katika muundo wa mviringo wa kupanua. Ikiwa radius ya mzunguko wa nyasi zinazowaka huongezeka kwa muda kulingana na formula\(r(t)=2t+1\), onyesha eneo hilo limechomwa kama kazi ya muda,\(t\) (dakika).

95) Tumia kazi uliyopata katika zoezi la awali ili kupata eneo la jumla lililochomwa baada ya\(5\) dakika.

Jibu

\(A(5)=\pi(2(5)+1)2=121\pi\)vitengo vya mraba

96) Radius\(r\), kwa inchi, ya puto ya spherical inahusiana na kiasi,\(V\), na\(r(V)=\sqrt[3]{\frac{3V}{4\pi}}\). Air hupigwa ndani ya puto, hivyo kiasi baada ya\(t\) sekunde hutolewa na\(V(t)=10+20t\).

1. Pata kazi ya composite\(r(V(t))\).
2. Pata wakati halisi wakati radius inakaribia inchi 10.

97) Idadi ya bakteria katika bidhaa za chakula cha friji hutolewa na\(N(T)=23T^2−56T+1\)\(3<T<33\),, wapi\(T\) joto la chakula. Wakati chakula kinapoondolewa kwenye jokofu, joto hutolewa na\(T(t)=5t+1.5\), wapi\(t\) wakati wa masaa.

1. Pata kazi ya composite\(N(T(t))\).
2. Pata muda (pande zote hadi sehemu mbili za decimal) wakati hesabu ya bakteria inafikia 6752.

Jibu

1. \(N(T(t))=23(5t+1.5)^2−56(5t+1.5)+1\)
2. \(3.38\)masaa

1.5: Mabadiliko ya Kazi

Mara nyingi tunapopewa tatizo, tunajaribu kutengeneza hali hiyo kwa kutumia hisabati kwa namna ya maneno, meza, grafu, na equations. Njia moja tunaweza kuajiri ni kukabiliana na grafu za msingi za kazi za toolkit ili kujenga mifano mpya kwa hali fulani. Kuna njia za utaratibu wa kubadilisha kazi ili kujenga mifano sahihi kwa matatizo tunayojaribu kutatua.

Maneno

1) Wakati wa kuchunguza fomu ya kazi ambayo ni matokeo ya mabadiliko mengi, unawezaje kuelezea mabadiliko ya usawa kutoka kwa mabadiliko ya wima?

Jibu

Matokeo ya mabadiliko ya usawa wakati mara kwa mara inaongezwa au imetolewa kutoka kwa pembejeo. Mabadiliko ya wima husababisha wakati mara kwa mara inaongezwa au imetolewa kutoka kwa pato.

2) Wakati wa kuchunguza fomu ya kazi ambayo ni matokeo ya mabadiliko mengi, unawezaje kusema kunyoosha usawa kutoka kunyoosha wima?

3) Wakati wa kuchunguza fomu ya kazi ambayo ni matokeo ya mabadiliko mengi, unawezaje kuwaambia compression usawa kutoka compression wima?

Jibu

Matokeo ya ukandamizaji usio na usawa wakati wa mara kwa\(1\) mara zaidi kuliko kuongezeka kwa pembejeo. matokeo compression wima wakati mara kwa mara kati\(0\) na\(1\) ni kuongezeka kwa pato.

4) Wakati wa kuchunguza fomu ya kazi ambayo ni matokeo ya mabadiliko mengi, unawezaje kuwaambia kutafakari kwa heshima na\(x\) -axis kutoka kwa kutafakari kwa heshima na\(y\) -axis?

5) Unawezaje kuamua kama kazi ni isiyo ya kawaida au hata kutoka kwa fomu ya kazi?

Jibu

Kwa ajili ya kazi\(f\), mbadala (-x) kwa (x) katika\(f(x)\). Kurahisisha. Ikiwa kazi inayosababisha ni sawa na kazi ya awali\(f(−x)=f(x)\), basi kazi ni hata. Ikiwa kazi inayosababisha ni kinyume cha kazi ya awali\(f(−x)=−f(x)\), basi kazi ya awali ni isiyo ya kawaida. Ikiwa kazi si sawa au kinyume, basi kazi sio isiyo ya kawaida wala hata.

Kialjebra

6) Andika fomu ya kazi iliyopatikana wakati grafu ya\(f(x)=\sqrt{x}\) imebadilishwa\(1\) kitengo na\(2\) vitengo vya kushoto.

7) Andika formula ya kazi iliyopatikana wakati grafu ya\(f(x)=|x|\) imebadilishwa\(3\) vitengo na\(1\) kitengo cha kulia.

Jibu

\(g(x)=|x-1|−3\)

8) Andika formula kwa ajili ya kazi iliyopatikana wakati grafu ya\(f(x)=\dfrac{1}{x}\) ni kubadilishwa chini\(4\) vitengo na\(3\) vitengo haki.

9) Andika fomu ya kazi iliyopatikana wakati grafu ya\(f(x)=\dfrac{1}{x^2}\) imebadilishwa\(2\) vitengo na\(4\) vitengo vya kushoto.

Jibu

\(g(x)=\dfrac{1}{(x+4)^2}+2\)

Kwa mazoezi 10-19, kuelezea jinsi grafu ya kazi ni mabadiliko ya grafu ya kazi ya awali\(f\).

10)\(y=f(x−49)\)

11)\(y=f(x+43)\)

Jibu

Grafu ya\(f(x+43)\) ni mabadiliko ya usawa kwa\(43\) vitengo vya kushoto vya grafu ya\(f\).

12)\(y=f(x+3)\)

13)\(y=f(x−4)\)

Jibu

Grafu ya\(f(x-4)\) ni mabadiliko ya usawa kwa\(4\) vitengo sahihi vya grafu ya\(f\).

14)\(y=f(x)+5\)

15)\(y=f(x)+8\)

Jibu

Grafu ya\(f(x)+8\) ni wima kuhama up\(8\) vitengo ya grafu ya\(f\).

16)\(y=f(x)−2\)

17)\(y=f(x)−7\)

Jibu

Grafu ya\(f(x)−7\) ni kuhama wima chini\(7\) vitengo ya grafu ya\(f\).

18)\(y=f(x−2)+3\)

19)\(y=f(x+4)−1\)

Jibu

Grafu ya\(f(x+4)−1\) ni mabadiliko ya usawa kwa\(4\) vitengo vya kushoto na mabadiliko ya wima chini ya\(1\) kitengo cha grafu ya\(f\).

Kwa mazoezi 20-23, tambua muda (s) ambao kazi inaongezeka na kupungua.

20)\(f(x)=4(x+1)^2−5\)

21)\(g(x)=5(x+3)^2−2\)

Jibu

kupungua\((−\infty,−3)\) na kuongezeka\((−3,\infty)\)

22)\(a(x)=\sqrt{−x+4}\)

23)\(k(x)=−3\sqrt{x}−1\)

Jibu

kupungua\((0, \infty)\)

Graphic

Kwa ajili ya mazoezi 24-26, kutumia grafu ya\(f(x)=2^x\) inavyoonekana katika Kielelezo hapa chini kwa mchoro grafu ya kila mabadiliko ya\(f(x)\).

\ (f (x)\).” style="upana: 301px; urefu: 306px;” width="301px” height="306px” src=” https://math.libretexts.org/@api/dek..._01_05_201.jpg "/>

Grafu ya\(f(x)\).

25)\(h(x)=2^x−3\)

24)\(g(x)=2^x+1\)

Jibu

\ (k (x)\)” src =” https://math.libretexts.org/@api/dek..._01_05_202.jpg "/>

Grafu ya\(k(x)\)

26)\(w(x)=2^x−1\)

Kwa mazoezi 27-30, mchoro grafu ya kazi kama mabadiliko ya grafu ya moja ya kazi za toolkit.

27)\(f(t)=(t+1)^2−3\)

Jibu

\ (f (t)\).” src=” https://math.libretexts.org/@api/dek..._01_05_206.jpg "/>

Grafu ya\(f(t)\).

28)\(h(x)=|x−1|+4\)

29)\(k(x)=(x−2)^3−1\)

Jibu

\ (k (x)\).” src=” https://math.libretexts.org/@api/dek..._01_05_208.jpg "/>

Grafu ya\(k(x)\).

30)\(m(t)=3+\sqrt{t+2}\)

Numeric

31) Tabular uwakilishi kwa ajili ya kazi\(f\)\(g\),, na\(h\) ni hapa chini. Andika\(g(x)\) na\(h(x)\) kama mabadiliko ya\(f(x)\).

\(x\)	-2	-1	0	1	2
\(f(x)\)	-2	-1	-3	1	2

\(x\)	-1	0	1	2	3
\(g(x)\)	-2	-1	-3	1	2

\(x\)	-2	-1	0	1	2
\(h(x)\)	-1	0	-2	2	3

Jibu

\(g(x)=f(x-1)\),\(h(x)=f(x)+1\)

32) Tabular uwakilishi kwa ajili ya kazi\(f\)\(g\),, na\(h\) ni hapa chini. Andika\(g(x)\) na\(h(x)\) kama mabadiliko ya\(f(x)\).

\(x\)	-2	-1	0	1	2
\(f(x)\)	-1	-3	4	2	1

\(x\)	-3	-2	-1	0	1
\(g(x)\)	-1	-3	4	2	1

\(x\)	-2	-1	0	1	2
\(h(x)\)	-2	-4	3	1	0

Kwa mazoezi 33-40, andika equation kwa kila kazi iliyopigwa kwa kutumia mabadiliko ya grafu ya kazi moja ya toolkit.

33)

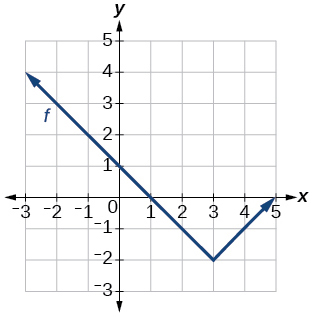
Grafu ya kazi kamili.

Jibu

\(f(x)=|x-3|−2\)

34)

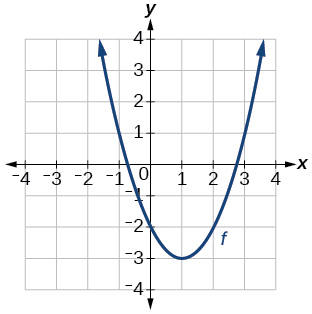
Grafu ya parabola.

35)

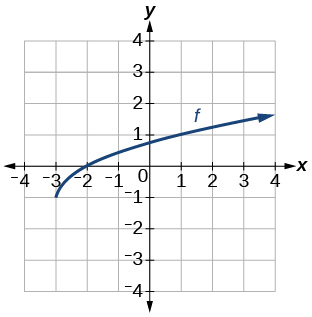
Grafu ya kazi ya mizizi ya mraba.

Jibu

\(f(x)=\sqrt{x+3}−1\)

36)

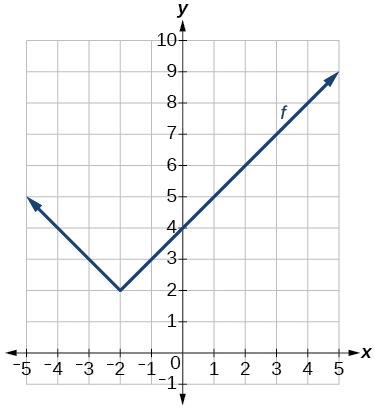
Grafu ya kazi kamili.

37)

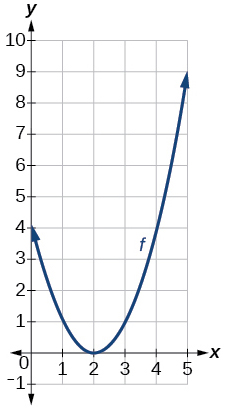
Grafu ya parabola

Jibu

\(f(x)=(x-2)^2\)

38)

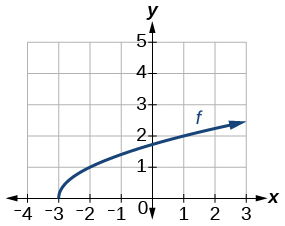
Grafu ya kazi ya mizizi ya mraba.

39)

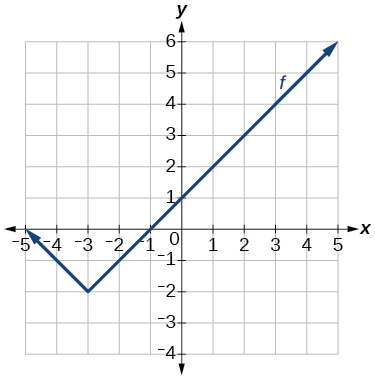
Grafu ya kazi kamili.

Jibu

\(f(x)=|x+3|−2\)

40)

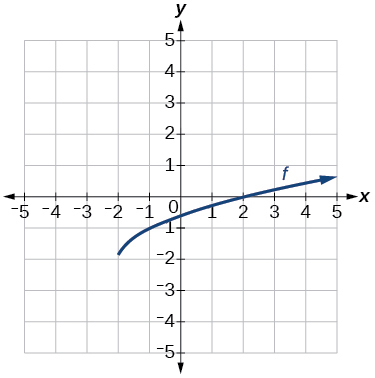
Grafu ya kazi ya mizizi ya mraba.

Kwa mazoezi 41-42, tumia grafu za mabadiliko ya kazi ya mizizi ya mraba ili kupata formula kwa kila kazi.

41)

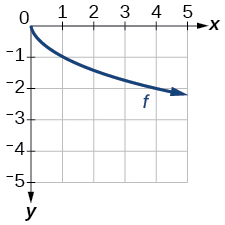
Grafu ya kazi ya mizizi ya mraba.

Jibu

\(f(x)=−\sqrt{x}\)

42)

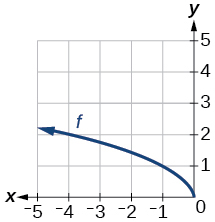
Grafu ya kazi ya mizizi ya mraba.

Kwa mazoezi 43-46, tumia grafu za kazi za toolkit zilizobadilishwa ili kuandika formula kwa kila kazi zinazosababisha.

43)

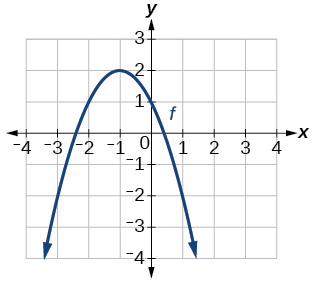
Grafu ya parabola.

Jibu

\(f(x)=−(x+1)^2+2\)

44)

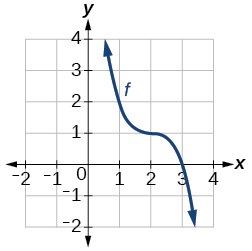
Grafu ya kazi ya ujazo.

45)

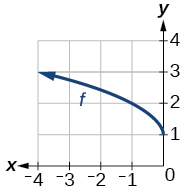
Grafu ya kazi ya mizizi ya mraba.

Jibu

\(f(x)=\sqrt{−x}+1\)

46)

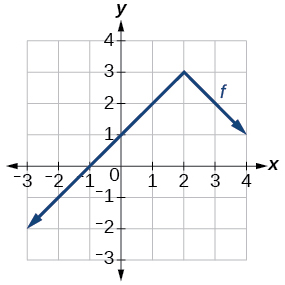
Grafu ya kazi kamili.

Kwa mazoezi 47-52, onyesha kama kazi ni isiyo ya kawaida, hata, au wala.

47)\(f(x)=3x^4\)

Jibu

hata

48)\(g(x)=\sqrt{x}\)

49)\(h(x)=\dfrac{1}{x}+3x\)

Jibu

isiyo ya kawaida

50)\(f(x)=(x−2)^2\)

51)\(g(x)=2x^4\)

Jibu

hata

52)\(h(x)=2x−x^3\)

Kwa mazoezi 53-62, kuelezea jinsi grafu ya kila kazi ni mabadiliko ya grafu ya kazi ya awali\(f\).

53)\(g(x)=−f(x)\)

Jibu

Grafu ya\(g\) ni kutafakari wima (katika x-axis) ya grafu ya\(f\).

54)\(g(x)=f(−x)\)

55)\(g(x)=4f(x)\)

Jibu

Grafu ya\(g\) ni kunyoosha wima kwa sababu ya 4 ya grafu ya\(f\).

56)\(g(x)=6f(x)\)

57)\(g(x)=f(5x)\)

Jibu

Grafu ya\(g\) ni compression usawa kwa sababu ya\(15\) ya grafu ya\(f\).

58)\(g(x)=f(2x)\)

59)\(g(x)=f \left(\dfrac{1}{3}x \right)\)

Jibu

Grafu ya\(g\) ni kunyoosha usawa kwa sababu ya 3 ya grafu ya\(f\).

60)\(g(x)=f \left(\dfrac{1}{5}x \right)\)

61)\(g(x)=3f(−x)\)

Jibu

Grafu ya\(g\) ni kutafakari usawa katika y-axis na kunyoosha wima kwa sababu ya 3 ya grafu ya\(f\).

62)\(g(x)=−f(3x)\)

Kwa mazoezi 63-68, weka fomu ya kazi\(g\) inayosababisha wakati grafu ya kazi ya toolkit iliyotolewa inabadilishwa kama ilivyoelezwa.

63) Grafu ya\(f(x)=|x|\) inaonekana juu ya\(y\) -axis na usawa USITUMIE na sababu ya\(\dfrac{1}{4}\).

Jibu

\(g(x)=|−4x|\)

64) Grafu ya\(f(x)=\sqrt{x}\) inaonekana juu ya\(x\) -axis na usawa aliweka kwa sababu ya\(2\).

65) Grafu ya\(f(x)=\dfrac{1}{x^2}\) ni wima USITUMIE kwa sababu ya\(\dfrac{1}{3}\), kisha kubadilishwa kwa\(2\) vitengo kushoto na\(3\) vitengo chini.

Jibu

\(g(x)=\dfrac{1}{3(x+2)^2}−3\)

66) Grafu ya\(f(x)=\dfrac{1}{x}\) ni wima aliweka kwa sababu ya\(8\), kisha kubadilishwa kwa\(4\) vitengo haki na juu\(2\) vitengo.

67) Grafu ya\(f(x)=x^2\) ni wima USITUMIE kwa sababu ya\(\dfrac{1}{2}\), kisha kubadilishwa kwa\(5\) vitengo haki na\(1\) kitengo juu.

Jibu

\(g(x)=\dfrac{1}{2}(x-5)^2+1\)

68) Grafu ya\(f(x)=x^2\) ni usawa aliweka kwa sababu ya\(3\), kisha kubadilishwa kwa\(4\) vitengo kushoto na\(3\) vitengo chini.

Kwa mazoezi 69-77, kuelezea jinsi formula ni mabadiliko ya kazi ya toolkit. Kisha mchoro grafu ya mabadiliko.

69)\(g(x)=4(x+1)^2−5\)

Jibu

Grafu ya kazi\(f(x)=x^2\) imebadilishwa kwenye\(1\) kitengo cha kushoto, imetambulishwa kwa wima kwa sababu ya\(4\), na kubadilishwa\(5\) vitengo.

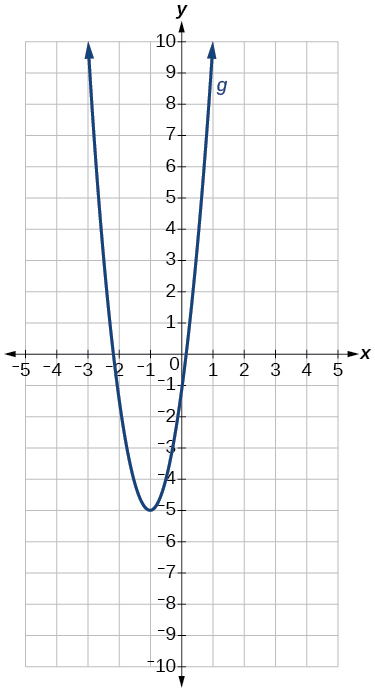
Grafu ya parabola.

70)\(g(x)=5(x+3)^2−2\)

71)\(h(x)=−2|x−4|+3\)

Jibu

Grafu ya\(f(x)=|x|\) imetambulishwa kwa wima kwa sababu ya\(2\), kubadilishwa\(4\) vitengo vya usawa kwa haki, yalijitokeza kwenye mhimili usio na usawa, na kisha ikabadilishwa\(3\) vitengo vya wima.

Grafu ya kazi kamili ya thamani.

72)\(k(x)=−3\sqrt{x}−1\)

73)\(m(x)=\dfrac{1}{2}x^3\)

Jibu

Grafu ya kazi\(f(x)=x^3\) imesisitizwa kwa wima kwa sababu ya\(\dfrac{1}{2}\).

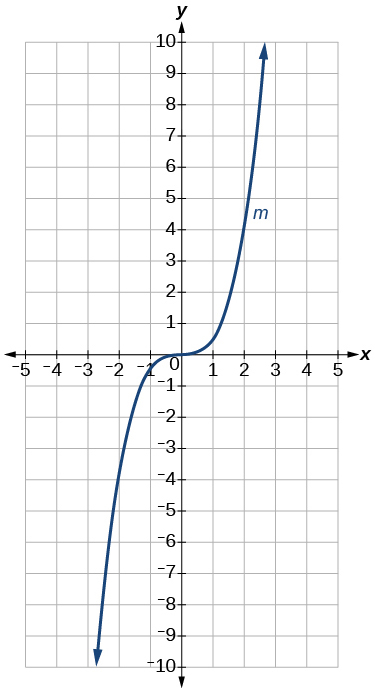
Grafu ya kazi ya ujazo.

74)\(n(x)=\dfrac{1}{3}|x−2|\)

75)\(p(x)=(\dfrac{1}{3}x)^3−3\)

Jibu

Grafu ya kazi imetambulishwa kwa usawa na sababu ya\(3\) na kisha ikabadilishwa kwa wima chini na\(3\) vitengo.

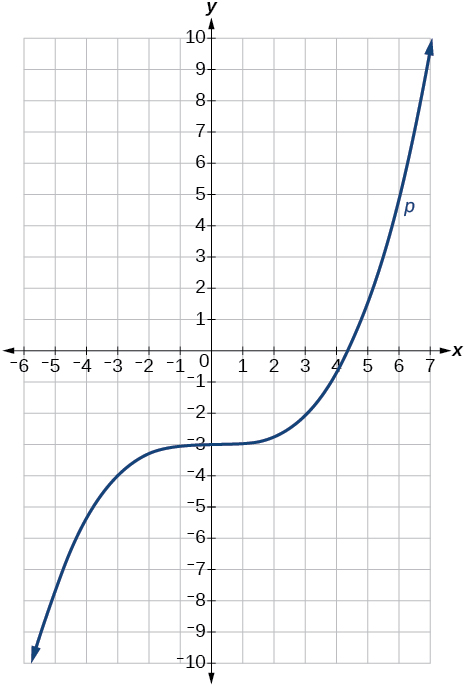
Grafu ya kazi ya ujazo.

76)\(q(x)=(\dfrac{1}{4}x)^3+1\)

77)\(a(x)=\sqrt{−x+4}\)

Jibu

Grafu ya\(f(x)=\sqrt{x}\) ni kubadilishwa\(4\) vitengo haki na kisha yalijitokeza katika mstari wima\(x=4\).

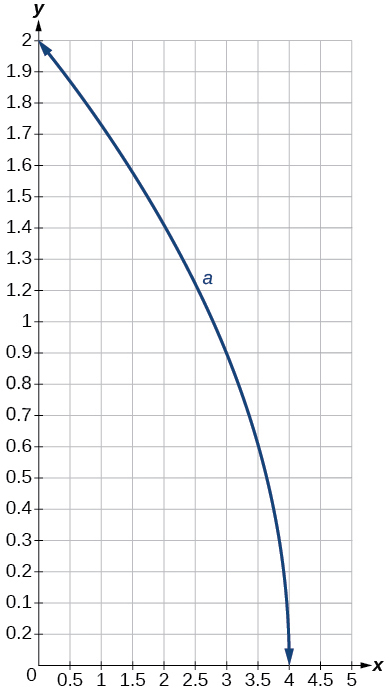
Grafu ya kazi ya mizizi ya mraba.

Kwa mazoezi 78-81, tumia grafu katika Kielelezo hapa chini ili mchoro mabadiliko yaliyotolewa.

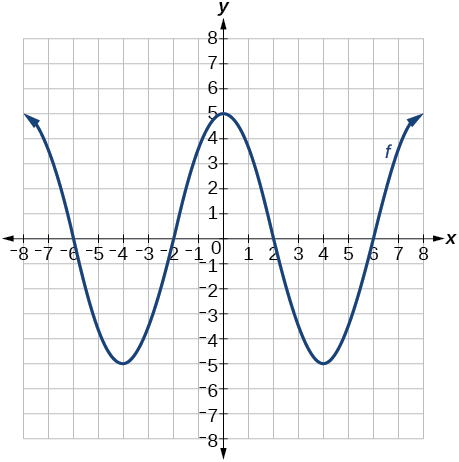
Grafu ya polynomial.

78)\(g(x)=f(x)−2\)

79)\(g(x)=−f(x)\)

Jibu

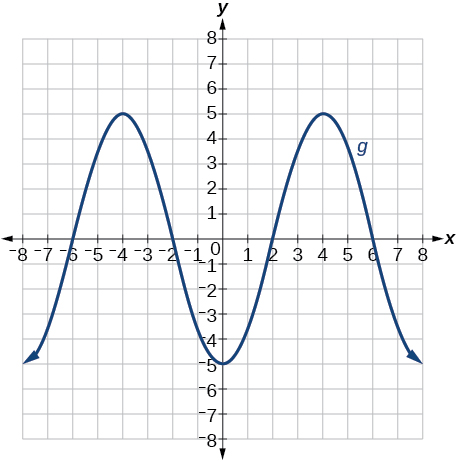
Grafu ya polynomial.

80)\(g(x)=f(x+1)\)

81)\(g(x)=f(x−2)\)

Jibu

Grafu ya polynomial.

1.6: Kazi kamili ya Thamani

Umbali katika ulimwengu unaweza kupimwa kwa pande zote. Kwa hivyo, ni muhimu kuzingatia umbali kama kazi ya thamani kamili. Katika sehemu hii, tutachunguza kazi za thamani kamili. Kazi ya thamani kamili ni kawaida hufikiriwa kama kutoa umbali nambari inatoka sifuri kwenye mstari wa nambari. Algebraically, kwa chochote thamani ya pembejeo ni, pato ni thamani bila kujali ishara.

Maneno

1) Je, unaweza kutatua equation thamani kamili?

Jibu

Isulate kabisa thamani mrefu ili equation ni ya fomu\(|A|=B\). Fomu equation moja kwa kuweka usemi ndani ya alama ya thamani kamili\(A\),, sawa na kujieleza upande wa pili wa equation,\(B\). Fomu equation pili kwa kuweka\(A\) sawa na kinyume cha kujieleza upande wa pili wa equation,\(−B\). Kutatua kila equation kwa variable.

2) Unawezaje kujua kama kazi ya thamani kamili ina mbili\(x\) -intercepts bila graphing kazi?

3) Wakati wa kutatua kazi ya thamani kamili, neno la thamani kamili la pekee ni sawa na idadi hasi. Je! Hiyo inakuambia nini kuhusu grafu ya kazi ya thamani kamili?

Jibu

Grafu ya kazi ya thamani kamili haina msalaba\(x\) -axis, hivyo grafu ni ama kabisa juu au kabisa chini ya\(x\) -axis.

4) Unawezaje kutumia grafu ya kazi ya thamani kamili ili kuamua maadili ya\(x\) maadili ambayo maadili ya kazi ni hasi?

5) Je, unaweza kutatua usawa wa thamani kamili algebraically?

Jibu

Kwanza kuamua pointi za mipaka kwa kutafuta suluhisho (s) ya equation. Tumia pointi za mipaka ili kuunda vipindi vya ufumbuzi iwezekanavyo. Chagua thamani ya mtihani katika kila kipindi ili ueleze maadili ambayo yanakidhi usawa.

Kialjebra

6) Eleza namba zote\(x\) zilizo\(4\) mbali na nambari\(8\). Eleza hii kwa kutumia nukuu ya thamani kamili.

7) Eleza namba zote\(x\) zilizo\(\dfrac{1}{2}\) mbali na nambari\(-4\). Eleza hii kwa kutumia nukuu ya thamani kamili.

Jibu

\(|x+4|= \dfrac{1}{2}\)

8) Eleza hali ambayo umbali huo\(x\) unatoka\(10\) ni angalau\(15\) vitengo. Eleza hii kwa kutumia nukuu ya thamani kamili.

9) Pata maadili yote ya kazi\(f(x)\) kama umbali kutoka\(f(x)\) kwa thamani\(8\) ni chini ya\(0.03\) vitengo. Eleza hii kwa kutumia nukuu ya thamani kamili.

Jibu

\(|f(x)−8|<0.03\)

Kwa mazoezi 10-24, tatua usawa hapa chini na ueleze jibu kwa kutumia alama ya kuweka.

10)\(|x+3|=9\)

11)\(|6−x|=5\)

Jibu

\({1,11}\)

12)\(|5x−2|=11\)

13)\(|4x−2|=11\)

Jibu

\(\left \{\dfrac{9}{4}, \dfrac{13}{4} \right \}\)

14)\(2|4−x|=7\)

15)\(3|5−x|=5\)

Jibu

\(\left \{\dfrac{10}{3},\dfrac{20}{3} \right \}\)

16)\(3|x+1|−4=5\)

17)\(5|x−4|−7=2\)

Jibu

\(\left \{\dfrac{11}{5}, \dfrac{29}{5} \right \}\)

18)\(0=−|x−3|+2\)

19)\(2|x−3|+1=2\)

Jibu

\(\left \{\dfrac{5}{2}, \dfrac{7}{2} \right \}\)

20)\(|3x−2|=7\)

21)\(|3x−2|=−7\)

Jibu

Hakuna ufumbuzi

22)\(\left |\dfrac{1}{2}x−5 \right |=11\)

23)\(\left |\dfrac{1}{3}x+5 \right |=14\)

Jibu

\(\{−57,27\}\)

24)\(−\left |\dfrac{1}{3}x+5 \right |+14=0\)

Kwa mazoezi 25-28, pata\(x\) - na\(y\) -intercepts ya grafu ya kila kazi.

25)\(f(x)=2|x+1|−10\)

Jibu

\((0,−8)\);\((−6,0)\),\((4,0)\)

26)\(f(x)=4|x−3|+4\)

27)\(f(x)=−3|x−2|−1\)

Jibu

\((0,−7)\);\(x\) hakuna-intercepts

28)\(f(x)=−2|x+1|+6\)

Kwa mazoezi 29-36, tatua kila usawa na uandike suluhisho katika maelezo ya muda.

29)\(| x−2 |>10\)

Jibu

\((−\infty,−8)\cup(12,\infty)\)

30)\(2|v−7|−4\geq42\)

31)\(|3x−4|\geq8\)

Jibu

\(−\dfrac{4}{3}{\leq}x\leq4\)

32)\(|x−4|\geq8\)

33)\(|3x−5|\geq-13\)

Jibu

\(\left (−\infty,− \dfrac{8}{3}\right ]\cup\left[6,\infty\right)\)

34)\(|3x−5|\geq−13\)

35)\(|\dfrac{3}{4}x−5|\geq7\)

Jibu

\(\left (-\infty,-\dfrac{8}{3}\right ]\cup\left[16,\infty\right)\)

36)\(\left |\dfrac{3}{4}x−5 \right |+1\leq16\)

Graphic

Kwa mazoezi 37-39, grafu ya thamani kamili ya kazi. Panda angalau pointi tano kwa mkono kwa kila grafu.

37)\(y=|x−1|\)

Jibu

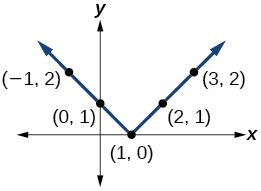
38)\(y=|x+1|\)

39)\(y=|x|+1\)

Jibu

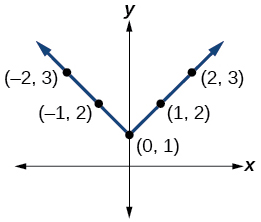
Kwa mazoezi 40-52, graph kazi zilizopewa kwa mkono.

40)\(y=|x|−2\)

41)\(y=−|x|\)

Jibu

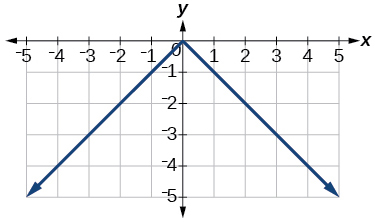
42)\(y=−|x|−2\)

43)\(y=−|x−3|−2\)

Jibu

44)\(f(x)=−|x−1|−2\)

45)\(f(x)=−|x+3|+4\)

Jibu

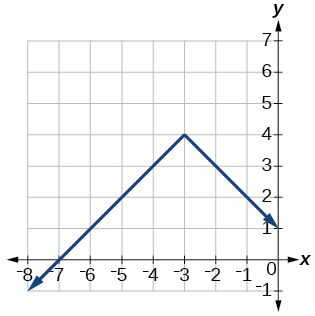
46)\(f(x)=2|x+3|+1\)

47)\(f(x)=3|x−2|+3\)

Jibu

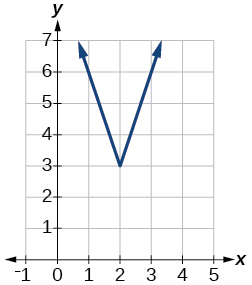
48)\(f(x)=|2x−4|−3\)

49)\(f(x)=|3x+9|+2\)

Jibu

50)\(f(x)=−|x−1|−3\)

51)\(f(x)=−|x+4|−3\)

Jibu

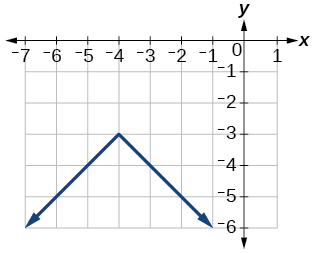
52)\(f(x)=\dfrac{1}{2}|x+4|−3\)

Teknolojia

53) Tumia matumizi ya graphing\(f(x)=10|x−2|\) kwenye grafu kwenye dirisha la kutazama\([0,4]\). Tambua aina inayofanana. Onyesha grafu.

Jibu

mbalimbali:\([0,20]\)

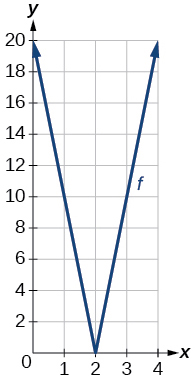
54) Tumia matumizi ya graphing\(f(x)=−100|x|+100\) kwenye grafu kwenye dirisha la kutazama\([−5,5]\). Tambua aina inayofanana. Onyesha grafu.

Kwa mazoezi 55-56, grafu kila kazi kwa kutumia matumizi ya graphing. Taja dirisha la kutazama.

55)\(f(x)=−0.1|0.1(0.2−x)|+0.3\)

Jibu

\(x\)-hukataa:

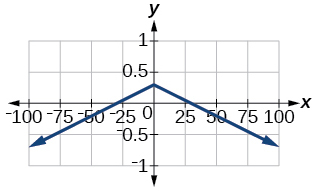
56)\(f(x)=4 \times10^{9}|x−(5 \times 10^9)|+2 \times10^9\)

Upanuzi

Kwa mazoezi 57-59, tatua usawa.

57)\(\left |−2x− \dfrac{2}{3}(x+1) \right |+3>−1\)

Jibu

\((−\infty,\infty)\)

58) Kama inawezekana, kupata maadili yote ya vile kwamba hakuna\(x\) -intercepts kwa\(f(x)=2|x+1|+a\).

59) Kama inawezekana, kupata maadili yote ya vile kwamba hakuna\(y\) -intercepts kwa\(f(x)=2|x+1|+a\).

Jibu

Hakuna ufumbuzi kwa ajili ya ambayo kuweka kazi kutoka kuwa na\(y\) -intercept. Thamani kamili kazi daima huvuka\(y\) -intercept wakati\(x=0\).

Real-World Matumizi

60) Miji A na B iko kwenye mstari huo wa mashariki-magharibi. Kudhani kwamba mji A iko katika asili. Ikiwa umbali kutoka mji A hadi mji B ni angalau\(100\) maili na\(x\) inawakilisha umbali kutoka mji B hadi mji A, onyesha hili kwa kutumia nukuu ya thamani kamili.

61) idadi ya kweli\(p\) ya watu ambao kutoa rating nzuri ya Congress ni\(8\%\) pamoja na kiasi cha makosa ya\(1.5\%\). Eleza kauli hii kwa kutumia equation thamani kamili.

Jibu

\(|p−0.08|\leq0.015\)

62) Wanafunzi ambao alama ndani ya\(18\) pointi ya idadi\(82\) watapita mtihani fulani. Andika kauli hii kwa kutumia thamani kabisa nukuu na kutumia variable\(x\) kwa alama.

63) Mchezaji lazima atoe kuzaa ambayo iko ndani ya\(0.01\) inchi ya kipenyo sahihi cha\(5.0\) inchi. Kutumia\(x\) kama kipenyo cha kuzaa, weka kauli hii kwa kutumia notation ya thamani kamili.

Jibu

\(|x−5.0|\leq0.01\)

64) Uvumilivu wa kuzaa mpira ni\(0.01\). Ikiwa kipenyo cha kweli cha kuzaa ni kuwa\(2.0\) inchi na thamani ya kipimo cha kipenyo ni\(x\) inchi, onyesha uvumilivu kwa kutumia nukuu ya thamani kamili.

1.7: Kazi za Inverse

Kama baadhi ya mashine ya kimwili inaweza kukimbia katika pande mbili, tunaweza kuuliza kama baadhi ya kazi “mashine” tumekuwa kusoma pia kukimbia nyuma. Katika sehemu hii, tutazingatia hali ya nyuma ya kazi.

Maneno

1) Eleza kwa nini mtihani wa mstari wa usawa ni njia bora ya kuamua kama kazi ni moja kwa moja?

Jibu

Kila pato la kazi lazima liwe na pato moja kwa kazi kuwa moja kwa moja. Kama mstari wowote usawa misalaba grafu ya kazi zaidi ya mara moja, hiyo ina maana kwamba\(y\) -maadili kurudia na kazi si moja kwa moja. Ikiwa hakuna mstari wa usawa unavuka grafu ya kazi zaidi ya mara moja, basi hakuna\(y\) maadili ya kurudia na kazi ni moja kwa moja.

2) Kwa nini sisi kuzuia uwanja wa kazi ya\(f(x)=x^2\) kupata inverse kazi ya?

3) Je, kazi inaweza kuwa inverse yake mwenyewe? Eleza.

Jibu

Ndiyo. Kwa mfano,\(f(x)=\dfrac{1}{x}\) ni inverse yake mwenyewe.

4) Je, kazi moja kwa moja ama daima kuongezeka au daima kupungua? Kwa nini au kwa nini?

5) Jinsi gani unaweza kupata inverse ya kazi algebraically?

Jibu

Kutokana na kazi\(y=f(x)\), kutatua\(x\) kwa suala la\(y\). Kubadilishana\(x\) na\(y\). Kutatua equation mpya kwa ajili ya\(y\). Maneno kwa\(y\) ni inverse,\(y=f^{-1}(x)\).

Kialjebra

6) Onyesha kwamba kazi\(f(x)=a−x\) ni inverse yake mwenyewe kwa namba zote halisi\(a\).

Kwa mazoezi 7-12, tafuta\(f^{-1}(x)\) kwa kila kazi.

7)\(f(x)=x+3\)

Jibu

\(f^{-1}(x)=x−3\)

8)\(f(x)=x+5\)

9)\(f(x)=2−x\)

Jibu

\(f^{-1}(x)=2−x\)

10)\(f(x)=3−x\)

11)\(f(x)=\dfrac{x}{x+2}\)

Jibu

\(f^{-1}(x)=\dfrac{−2x}{x−1}\)

12)\(f(x)=\dfrac{2x+3}{5x+4}\)

Kwa mazoezi 13-16, tafuta uwanja ambao kila kazi\(f\) ni moja kwa moja na isiyo ya kupungua. Andika kikoa katika maelezo ya muda. Kisha tafuta inverse ya\(f\) vikwazo kwenye uwanja huo.

13)\(f(x)=(x+7)^2\)

Jibu

uwanja wa\(f(x)\):\(\left[−7,\infty\right)\);\(f^{-1}(x)=\sqrt{x}−7\)

14)\(f(x)=(x−6)^2\)

15)\(f(x)=x^2−5\)

Jibu

uwanja wa\(f(x)\):\(\left[0,\infty\right)\);\(f^{-1}(x)=\sqrt{x+5}\)

16) Kutokana\(f(x)=\dfrac{x}{2+x}\) na\(g(x)=\dfrac{2x}{1-x}:\)

1. Kupata\(f(g(x))\) na\(g(f(x))\).
2. Jibu linatuambia nini kuhusu uhusiano kati\(f(x)\) na\(g(x)?\)

Jibu

a.\(f(g(x))=x\) na\(g(f(x))=x\)

b Hii inatuambia kwamba\(f\) na\(g\) ni kazi inverse

Kwa mazoezi 17-18, tumia utungaji wa kazi ili uhakikishe kuwa\(f(x)\) na kazi\(g(x)\) za inverse.

17)\(f(x)=\sqrt[3]{x-1}\) na\(g(x)=x^3+1\)

Jibu

\(f(g(x))=x\),\(g(f(x))=x\)

18)\(f(x)=−3x+5\) na\(g(x)=\dfrac{x-5}{-3}\)

Graphic

Kwa mazoezi 19-22, tumia matumizi ya graphing ili kuamua kama kila kazi ni moja kwa moja.

19)\(f(x)=\sqrt{x}\)

Jibu

moja kwa moja

20)\(f(x)=\sqrt[3]{3x+1}\)

21)\(f(x)=−5x+1\)

Jibu

moja kwa moja

22)\(f(x)=x^3−27\)

Kwa mazoezi 23-24, onyesha kama grafu inawakilisha kazi moja kwa moja.

23)

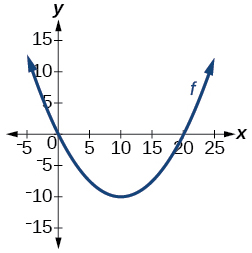
Jibu

si moja kwa moja

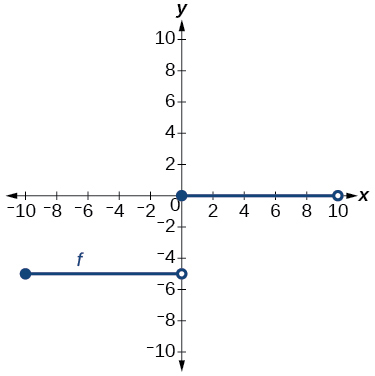
24)

Kielelezo hapa chini.

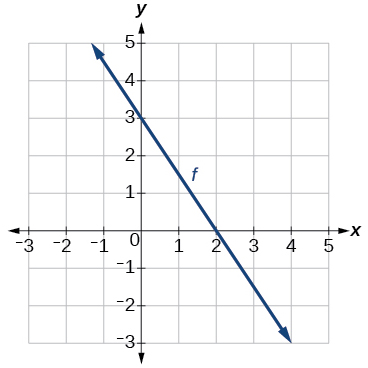
Grafu ya mstari

25) Kupata\(f(0)\).

Jibu

\(3\)

26) Tatua\(f(x)=0\).

27) Kupata\(f^{-1}(0)\).

Jibu

\(2\)

28) Tatua\(f^{-1}(x)=0\).

Kwa mazoezi 29-32, tumia grafu ya kazi moja kwa moja iliyoonyeshwa kwenye Kielelezo hapa chini

Grafu ya kazi ya mizizi ya mraba.

29) Mchoro graph ya\(f^{-1}\).

Jibu

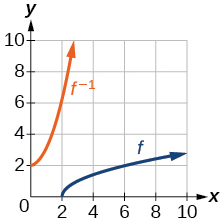
30) Kupata\(f(6)\) na\(f^{-1}(2)\).

31) Kama grafu kamili ya\(f\) inavyoonekana, kupata uwanja wa\(f\).

Jibu

\([2,10]\)

32) Ikiwa grafu kamili ya\(f\) inavyoonyeshwa, pata aina mbalimbali\(f\)

Numeric

Kwa mazoezi 33-36, tathmini au kutatua, kudhani kuwa kazi\(f\) ni moja kwa moja.

33) Kama\(f(6)=7\), kupata\(f^{-1}(7)\).

Jibu

\(6\)

34) Kama\(f(3)=2\), kupata\(f^{-1}(2)\).

35) Kama\(f^{-1}(−4)=−8\), kupata\(f(−8)\).

Jibu

\(-4\)

36) Kama\(f^{-1}(−2)\) =-1, tafuta\(f(−1)\).

Kwa mazoezi 37-40, tumia maadili yaliyoorodheshwa kwenye Jedwali hapa chini ili kutathmini au kutatua.

\(x\)	\(f(x)\)
\ (x\) "> 0	\ (f (x)\) "> 8
\ (x\) ">1	\ (f (x)\) "> 0
\ (x\) "> 2	\ (f (x)\) "> 7
\ (x\) ">3	\ (f (x)\) "> 4
\ (x\) ">4	\ (f (x)\) "> 2
\ (x\) "> 5	\ (f (x)\) "> 6
\ (x\) ">6	\ (f (x)\) "> 5
\ (x\) ">7	\ (f (x)\) "> 3
\ (x\) ">8	\ (f (x)\) "> 9
\ (x\) ">9	\ (f (x)\) "> 1

37) Kupata\(f(1)\).

Jibu

\(0\)

38) Tatua\(f(x)=3\).

39) Kupata\(f^{-1}(0)\).

Jibu

\(1\)

40) Kutatua\(f^{-1}(x)=7\).

41) Tumia uwakilishi wa tabular wa\(f\) katika Jedwali hapa chini ili kuunda meza kwa\(f^{-1}(x)\).

\(x\)	3	6	9	13	14
\(f(x)\)	1	4	7	12	16

Jibu

\(x\)	1	4	7	12	16
\(f^{-1}(x)\)	3	6	9	13	14

Teknolojia

Kwa mazoezi 42-44, tafuta kazi ya inverse. Kisha, graph kazi na inverse yake.

42)\(f(x)=\dfrac{3}{x-2}\)

43)\(f(x)=x^3−1\)

Jibu

\(f^{-1}(x)=(1+x)^{1/3}\)

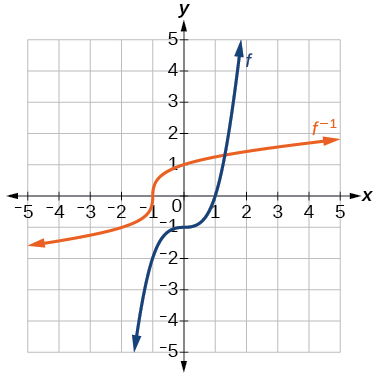
44) Kupata kazi inverse ya\(f(x)=\dfrac{1}{x-1}\). Tumia matumizi ya graphing ili kupata uwanja wake na upeo. Andika kikoa na upeo katika maelezo ya muda.

Real-World Matumizi

45) Ili kubadilisha kutoka\(x\) digrii Celsius hadi\(y\) digrii Fahrenheit, tunatumia formula\(f(x)=\dfrac{9}{5}x+32\). Pata kazi ya inverse, ikiwa iko, na ueleze maana yake.

Jibu

\(f^{-1}(x)=\dfrac{5}{9}(x−32)\). Kutokana na joto la Fahrenheit\(x\), formula hii inakuwezesha kuhesabu joto la Celsius.

46) Mzunguko\(C\) wa mduara ni kazi ya radius yake iliyotolewa na\(C(r)=2{\pi}r\). Eleza radius ya mduara kama kazi ya mzunguko wake. Piga kazi hii\(r(C)\). Pata\(r(36\pi)\) na kutafsiri maana yake.

47) Gari linasafiri kwa kasi ya\(50\) maili kwa saa. umbali gari kusafiri katika maili ni kazi ya muda,\(t\), katika masaa iliyotolewa na\(d(t)=50t\). Pata kazi ya inverse kwa kuelezea wakati wa kusafiri kwa suala la umbali uliosafiri. Piga kazi hii\(t(d)\). Pata\(t(180)\) na kutafsiri maana yake.

Jibu

\(t(d)=\dfrac{d}{50}\),\(t(180)=\dfrac{180}{50}\). Wakati wa gari kusafiri\(180\) maili ni\(3.6\) masaa.