1.R: Kazi (Mapitio)
- Page ID
- 181169
1.1: Kazi na Uthibitishaji wa Kazi
Kwa mazoezi 1-4, onyesha kama uhusiano ni kazi.
1)\(\{(a,b),(c,d),(e,d)\}\)
- Jibu
-
kazi
2)\(\{(5,2),(6,1),(6,2),(4,8)\}\)
3)\(y^2+4=x\)
- Jibu
-
si kazi
4) Je, grafu katika Kielelezo chini ya kazi?
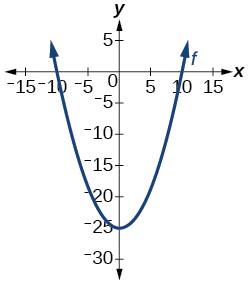
Kwa mazoezi 5-6, tathmini kazi katika maadili yaliyoonyeshwa:\(f(-3); f(2); f(-a); -f(a); f(a+h)\)
5)\(f(x)=-2x^2+3x\)
- Jibu
-
\(f(-3)=-27; f(2)=-2;f(-a)=-2a^2-3a;-f(a)=2a^2-3a;f(a+h)=-2a^2+3a-4ah+3h-2h^2\)
6)\(f(x)=2|3x-1|\)
Kwa mazoezi 7-8, onyesha kama kazi ni moja kwa moja.
7)\(f(x)=-3 x+5\)
- Jibu
-
moja kwa moja
8)\(f(x)=|x-3|\)
Kwa mazoezi 9-11, tumia mtihani wa mstari wa wima ili uone kama uhusiano ambao grafu hutolewa ni kazi.
9)
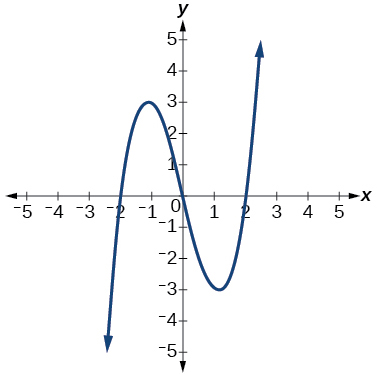
- Jibu
-
kazi
10)
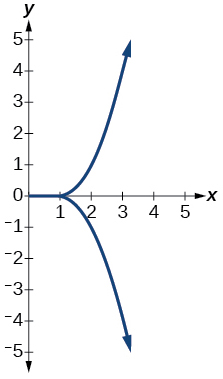
11)
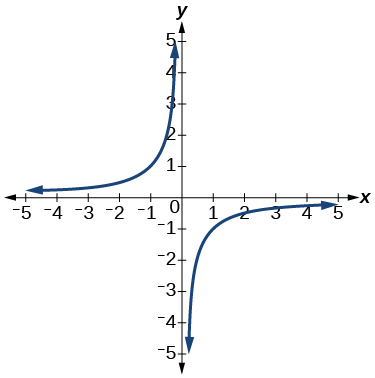
- Jibu
-
kazi
Kwa mazoezi 12-13, graph kazi.
12)\(f(x)=|x+1|\)
13)\(f(x)=x^{2}-2\)
- Jibu
-
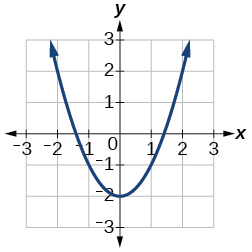
Kwa mazoezi 14-17, tumia Kielelezo hapa chini ili takriban maadili.
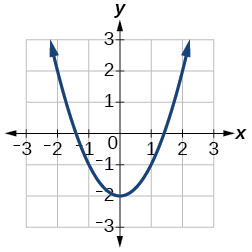
14)\(f(2)\)
15)\(f(-2)\)
- Jibu
-
\(2\)
16) Ikiwa\(f(x)=-2\), basi tatua\(x\)
17) Ikiwa\(f(x)=1\), basi tatua\(x\)
- Jibu
-
\(x=-1.8\)au\(x=1.8\)
Kwa mazoezi 18-19, tumia kazi\(h(t)=-16 t^{2}+80t\) ili kupata maadili.
18)\(\dfrac{h(2)-h(1)}{2-1}\)
19)\(\dfrac{h(a)-h(1)}{a-1}\)
- Jibu
-
\(\dfrac{-64+80 a-16 a^{2}}{-1+a}=-16 a+64\)
1.2: Domain na Range
Kwa mazoezi 1-4, tafuta uwanja wa kila kazi, ukielezea majibu kwa kutumia notation ya muda.
1)\(f(x)=\dfrac{2}{3 x+2}\)
2)\(f(x)=\frac{x-3}{x^{2}-4 x-12}\)
- Jibu
-
\((-\infty,-2) \cup(-2,6) \cup(6, \infty)\)
3)
4) Graph kazi hii piecewise:\(f(x)=\left\{\begin{array}{ll}{x+1} & {x<-2} \\ {-2 x-3} & {x \geq-2}\end{array}\right.\)
- Jibu
-
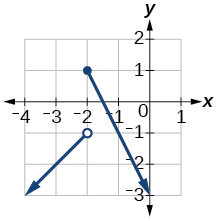
1.3: Viwango vya Mabadiliko na Tabia ya Grafu
Kwa mazoezi 1-3, pata kiwango cha wastani cha mabadiliko ya kazi kutoka\(x=1\) kwa\(x=2\)
1)\(f(x)=4 x-3\)
2)\(f(x)=10 x^{2}+x\)
- Jibu
-
\(31\)
3)\(f(x)=-\dfrac{2}{x^{2}}\)
Kwa mazoezi 4-6, tumia grafu ili kuamua vipindi ambavyo kazi zinaongezeka, kupungua, au mara kwa mara.
4)
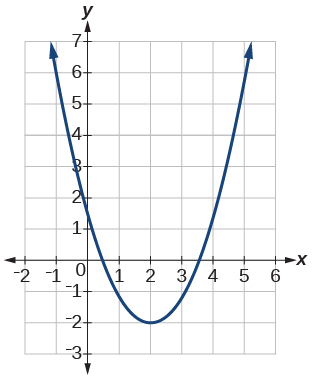
- Jibu
-
kuongezeka\((2, \infty)\); kupungua\((-\infty, 2)\)
5)
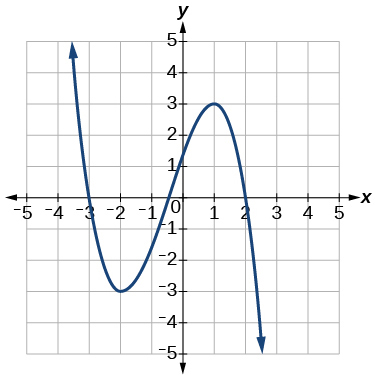
6)
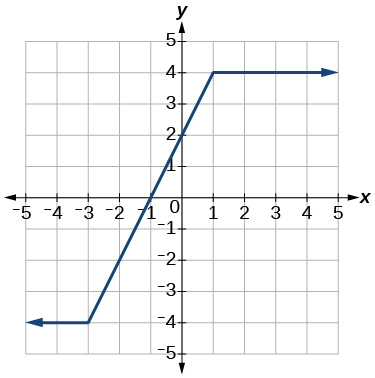
- Jibu
-
kuongezeka\((-3,1)\); mara kwa mara\((-\infty,-3) \cup(1, \infty)\)
7) Kupata chini ya ndani ya kazi graphed katika Zoezi 4.
8) Kupata extrema mitaa kwa ajili ya kazi graphed katika Zoezi 5.
- Jibu
-
kiwango cha chini cha ndani\((-2,-3)\); upeo wa ndani\((1,3)\)
9) Kwa grafu katika Kielelezo katika Zoezi 10, uwanja wa kazi ni\([-3,3]\). Mipangilio ni\([-10,10]\). Pata kiwango cha chini kabisa cha kazi kwa kipindi hiki.
10) Pata upeo kamili wa kazi iliyowekwa kwenye Kielelezo hapa chini.
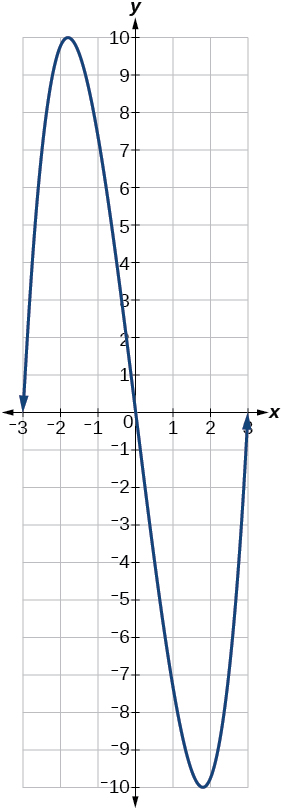
- Jibu
-
\((-1.8,10)\)
1.4: Muundo wa Kazi
Kwa mazoezi 1-5, tafuta\((f \circ g)(x)\) na\((g \circ f)(x)\) kwa kila jozi ya kazi.
1)\(f(x)=4-x, g(x)=-4x\)
2)\(f(x)=3 x+2, g(x)=5-6x\)
- Jibu
-
\((f \circ g)(x)=17-18 x ;(g \circ f)(x)=-7-18x\)
3)\(f(x)=x^{2}+2 x, g(x)=5 x+1\)
4)\(f(x)=\sqrt{x+2}, g(x)=\dfrac{1}{x}\)
- Jibu
-
\((f \circ g)(x)=\sqrt{\dfrac{1}{x}+2} ;(g \circ f)(x)=\dfrac{1}{\sqrt{x+2}}\)
5)\(f(x)=\dfrac{x+3}{2}, g(x)=\sqrt{1-x}\)
Kwa mazoezi 6-9, tafuta\((f \circ g)\) na kikoa\((f \circ g)(x)\) kwa kila jozi ya kazi.
6)\(f(x)=\frac{x+1}{x+4}, g(x)=\frac{1}{x}\)
- Jibu
-
\((f \circ g)(x)=\dfrac{1+x}{1+4 x}, x \neq 0, x \neq-\dfrac{1}{4}\)
7)\(f(x)=\dfrac{1}{x+3}, g(x)=\dfrac{1}{x-9}\)
8)\(f(x)=\dfrac{1}{x}, g(x)=\sqrt{x}\)
- Jibu
-
\((f \circ g)(x)=\frac{1}{\sqrt{x}}, x>0\)
9)\(f(x)=\frac{1}{x^{2}-1}, g(x)=\sqrt{x+1}\)
Kwa mazoezi 10-11, onyesha kila kazi\(H\) kama muundo wa kazi mbili\(f\) na\(g\) wapi\(H(x)=(f \circ g)(x)\)
10)\(H(x)=\sqrt{\frac{2 x-1}{3 x+4}}\)
- Jibu
-
sampuli:\(g(x)=\dfrac{2 x-1}{3 x+4}; f(x)=\sqrt{x}\)
11)\(H(x)=\dfrac{1}{\left(3 x^{2}-4\right)^{-3}}\)
1.5: Mabadiliko ya Kazi
Kwa mazoezi 1-8, mchoro grafu ya kazi iliyotolewa.
1)\(f(x)=(x-3)^{2}\)
- Jibu
-
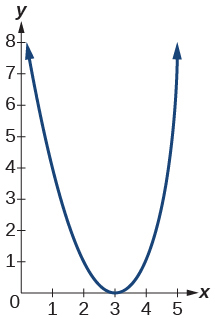
2)\(f(x)=(x+4)^{3}\)
3)\(f(x)=\sqrt{x}+5\)
- Jibu
-
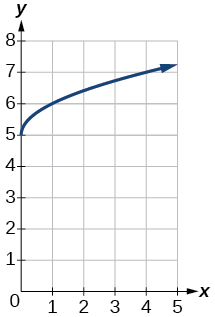
4)\(f(x)=-x^{3}\)
5)\(f(x)=\sqrt[3]{-x}\)
- Jibu
-
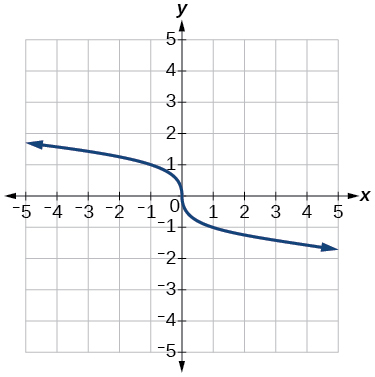
6)\(f(x)=5 \sqrt{-x}-4\)
7)\(f(x)=4[|x-2|-6]\)
- Jibu
-
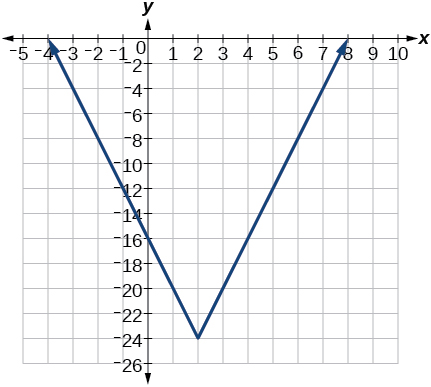
8)\(f(x)=-(x+2)^{2}-1\)
Kwa mazoezi 9-10, mchoro grafu ya kazi\(g\) ikiwa grafu ya kazi\(f\) inavyoonekana kwenye Mchoro hapa chini.
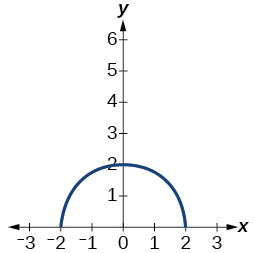
9)\(g(x)=f(x-1)\)
- Jibu
-
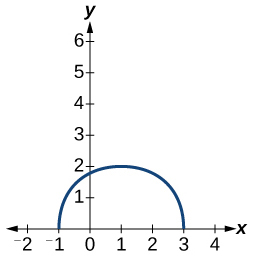
10)\(g(x)=3 f(x)\)
Kwa mazoezi 11-12, andika equation kwa kazi ya kawaida iliyowakilishwa na kila grafu hapa chini.
11)
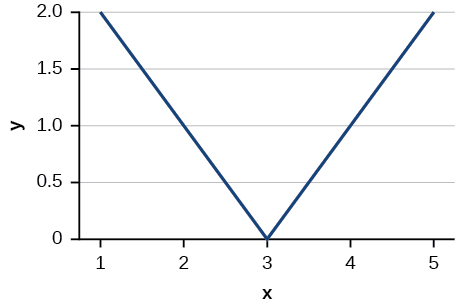
- Jibu
-
\(f(x)=|x-3|\)
12)
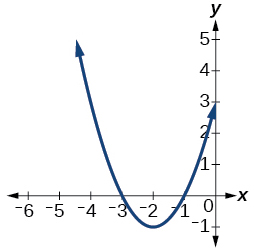
Kwa mazoezi 13-15, onyesha kama kila kazi hapa chini ni hata, isiyo ya kawaida, au wala.
13)\(f(x)=3 x^{4}\)
- Jibu
-
hata
14)\(g(x)=\sqrt{x}\)
15)\(h(x)=\frac{1}{x}+3 x\)
- Jibu
-
isiyo ya kawaida
Kwa mazoezi 16-18, kuchambua grafu na kuamua kama kazi iliyopigwa ni hata, isiyo ya kawaida, au wala.
16)
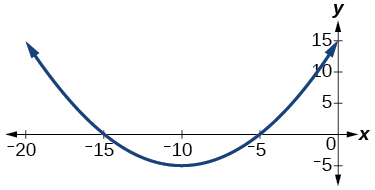
17)
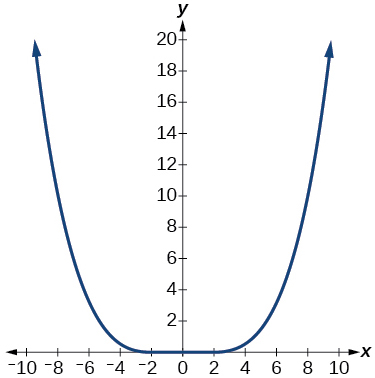
- Jibu
-
hata
18)
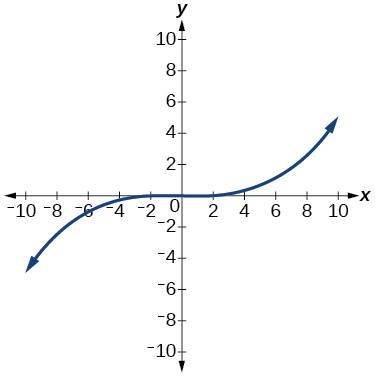
1.6: Kazi kamili ya Thamani
Kwa ajili ya mazoezi 1-3, kuandika equation kwa ajili ya mabadiliko ya\(f(x)=|x|\).
1)
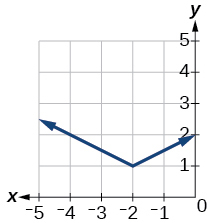
- Jibu
-
\(f(x)=\dfrac{1}{2}|x+2|+1\)
2)
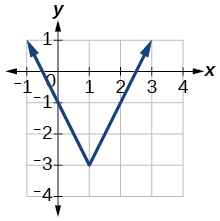
3)
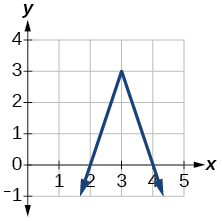
- Jibu
-
\(f(x)=-3|x-3|+3\)
Kwa mazoezi 4-6, grafu ya thamani kamili ya kazi.
4)\(f(x)=|x-5|\)
5)\(f(x)=-|x-3|\)
- Jibu
-
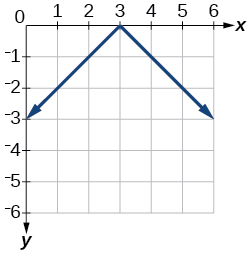
6)\(f(x)=|2 x-4|\)
Kwa mazoezi 7-8, tatua usawa wa thamani kamili.
7)\(|x+4|=18\)
- Jibu
-
\(x=-22, x=14\)
8)\(\left|\dfrac{1}{3} x+5\right|=\left|\dfrac{3}{4} x-2\right|\)
Kwa mazoezi 9-10, tatua usawa na ueleze suluhisho kwa kutumia notation ya muda.
9)\(|3 x-2|<7\)
- Jibu
-
\(\left(-\dfrac{5}{3}, 3\right)\)
10)\(\left|\dfrac{1}{3} x-2\right| \leq 7\)
1.7: Kazi za Inverse
Kwa mazoezi 1-2, tafuta\(f^{-1}(x)\) kwa kila kazi.
1)\(f(x)=9+10 x\)
2)\(f(x)=\dfrac{x}{x+2}\)
- Jibu
-
\(f^{-1}(x)=\dfrac{-2 x}{x-1}\)
3) Kwa zoezi zifuatazo, pata uwanja ambao kazi hiyo\(f\) ni moja kwa moja na isiyo ya kupungua. Andika kikoa katika maelezo ya muda. Kisha tafuta inverse ya\(f\) vikwazo kwenye uwanja huo. \[f(x)=x^{2}+1\]
4) Kutokana\(f(x)=x^{3}-5\) na\(g(x)=\sqrt[3]{x+5} \):
- Kupata\(f(g(x))\) na\(g(f(x))\).
- Jibu linatuambia nini kuhusu uhusiano kati\(f(x)\) na\(g(x) ?\)
- Jibu
-
- \(f(g(x))=x\)na\(g(f(x))=x\)
- Hii inatuambia kwamba\(f\) na\(g\) ni kazi inverse
Kwa mazoezi 5-8, tumia matumizi ya graphing ili kuamua kama kila kazi ni moja kwa moja.
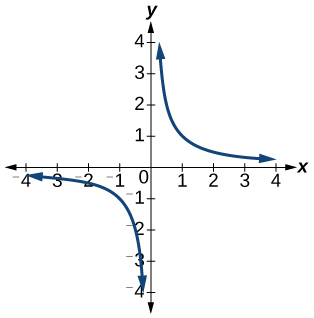
5)\(f(x)=\dfrac{1}{x}\)
- Jibu
-
Kazi ni moja kwa moja.
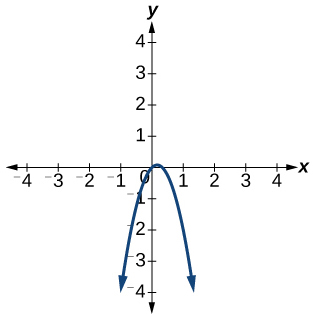
6)\(f(x)=-3 x^{2}+x\)
- Jibu
-
Kazi sio moja kwa moja.
7) Ikiwa\(f(5)=2,\) hupata\(f^{-1}(2)\)
- Jibu
-
\(5\)
8) Ikiwa\(f(1)=4,\) hupata\(f^{-1}(4)\)
Mazoezi mtihani
Kwa mazoezi 1-2, onyesha kama kila moja ya mahusiano yafuatayo ni kazi.
1)\(y=2 x+8\)
- Jibu
-
Uhusiano ni kazi.
2)\(\{(2,1),(3,2),(-1,1),(0,-2)\}\)
Kwa mazoezi 3-4, tathmini kazi\(f(x)=-3 x^{2}+2 x\) katika pembejeo iliyotolewa.
3)\(f(-2)\)
- Jibu
-
\(-16\)
4)\(f(a)\)
5) Onyesha kwamba kazi\(f(x)=-2(x-1)^{2}+3\) sio moja kwa moja.
- Jibu
-
Grafu ni parabola na grafu inashindwa mtihani wa mstari usio na usawa.
6) Andika kikoa cha kazi\(f(x)=\sqrt{3-x}\) katika maelezo ya muda.
7) Kupewa\(f(x)=2 x^{2}-5 x,\) kupata\(f(a+1)-f(1)\)
- Jibu
-
\(2 a^{2}-a\)
8) Graph kazi\(f(x)=\left\{\begin{array}{ccc}{x+1} & {\text { if }} & {-2<x<3} \\ {-x} & {\text { if }} & {x \geq 3}\end{array}\right.\)
9) Pata kiwango cha wastani cha mabadiliko ya kazi\(f(x)=3-2 x^{2}+x\) kwa kutafuta\(\dfrac{f(b)-f(a)}{b-a}\)
- Jibu
-
\(-2(a+b)+1\)
Kwa mazoezi 10-11, tumia kazi\(f(x)=3-2 x^{2}+x\) na\(g(x)=\sqrt{x}\) kupata kazi za composite.
10)\((g \circ f)(x)\)
11)\((g \circ f)(1)\)
- Jibu
-
\(\sqrt{2}\)
12)\(H(x)=\sqrt[3]{5 x^{2}-3 x}\) Eleza muundo wa kazi mbili,\(f\) na\(g,\) wapi\((f \circ g)(x)=H(x)\)
Kwa mazoezi 13-14, graph kazi kwa kutafsiri, kunyoosha, na/au compressing kazi toolkit.
13)\(f(x)=\sqrt{x+6}-1\)
- Jibu
-
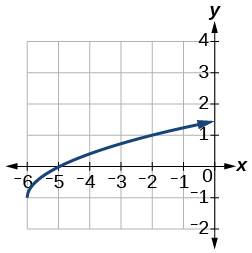
14)\(f(x)=\dfrac{1}{x+2}-1\)
Kwa mazoezi 15-17, onyesha kama kazi ni hata, isiyo ya kawaida, au wala.
15)\(f(x)=-\dfrac{5}{x^{2}}+9 x^{6}\)
- Jibu
-
hata
16)\(f(x)=-\dfrac{5}{x^{3}}+9 x^{5}\)
17)\(f(x)=\dfrac{1}{x}\)
- Jibu
-
isiyo ya kawaida
18) Graph thamani kamili kazi\(f(x)=-2|x-1|+3\).
19) Tatua\(|2 x-3|=17\).
- Jibu
-
\(x=-7\)na\(x=10\)
20) Tatua\(-\left|\dfrac{1}{3} x-3\right| \geq 17\). Eleza suluhisho katika maelezo ya muda.
Kwa mazoezi 21-22, tafuta inverse ya kazi.
21)\(f(x)=3 x-5\)
- Jibu
-
\(f^{-1}(x)=\dfrac{x+5}{3}\)
22)\(f(x)=\dfrac{4}{x+7}\)
Kwa mazoezi 23-26, tumia grafu ya\(g\) inavyoonekana kwenye Kielelezo hapa chini.
23) Je! Kazi inaongezeka kwa vipindi gani?
- Jibu
-
\((-\infty,-1.1)\)na\((1.1, \infty)\)
24) Kwa vipindi gani kazi inapungua?
25) Takriban kiwango cha chini cha kazi. Eleza jibu kama jozi iliyoamriwa.
- Jibu
-
\((1.1,-0.9)\)
26) Takriban upeo wa ndani wa kazi. Eleza jibu kama jozi iliyoamriwa.
Kwa mazoezi 27-29, tumia grafu ya kazi ya kipande kilichoonyeshwa kwenye Kielelezo hapa chini.
27) Kupata\(f(2)\).
- Jibu
-
\(f(2)=2\)
28) Tafuta\(f(-2)\).
29) Andika equation kwa kazi ya kipande.
- Jibu
-
\(f(x)=\left\{\begin{array}{cl}{|x|} & {\text { if } x \leq 2} \\ {3} & {\text { if } x>2}\end{array}\right.\)
Kwa mazoezi 30-35, tumia maadili yaliyoorodheshwa katika Jedwali hapa chini.
| \(x\) | \(F(x)\) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
| 6 | 13 |
| 7 | 15 |
| 8 | 17 |
30) Kupata\(F(6)\).
31) Tatua equation\(F(x)=5\)
- Jibu
-
\(x=2\)
32) Je, grafu inaongezeka au kupungua kwenye uwanja wake?
33) Je! Kazi inawakilishwa na grafu moja kwa moja?
- Jibu
-
ndiyo
34) Tafuta\(F^{-1}(15)\).
35) Kupewa\(f(x)=-2 x+11,\) kupata\(f^{-1}(x)\).
- Jibu
-
\(f^{-1}(x)=-\dfrac{x-11}{2}\)


