1.7: Kazi za Inverse

Last updated
Save as PDF

Page ID: 181155

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Thibitisha kazi inverse.
Tambua kikoa na upeo wa kazi ya inverse, na uzuie uwanja wa kazi ili uifanye moja kwa moja.
Kupata au kutathmini inverse ya kazi.
Tumia grafu ya kazi moja kwa moja ili kuunda kazi yake ya inverse kwenye shaba sawa.

Pampu ya joto inayobadilishwa ni mfumo wa kudhibiti hali ya hewa ambayo ni kiyoyozi na heater katika kifaa kimoja. Inaendeshwa katika mwelekeo mmoja, hupiga joto nje ya nyumba ili kutoa baridi. Uendeshaji kwa reverse, hupiga joto ndani ya jengo kutoka nje, hata katika hali ya hewa ya baridi, kutoa joto. Kama heater, pampu ya joto ni mara kadhaa ufanisi zaidi kuliko inapokanzwa kawaida umeme upinzani.

Kama baadhi ya mashine ya kimwili inaweza kukimbia katika pande mbili, tunaweza kuuliza kama baadhi ya kazi “mashine” tumekuwa kusoma pia kukimbia nyuma. Kielelezo$\PageIndex{1}$ hutoa uwakilishi Visual ya swali hili. Katika sehemu hii, tutazingatia hali ya nyuma ya kazi.

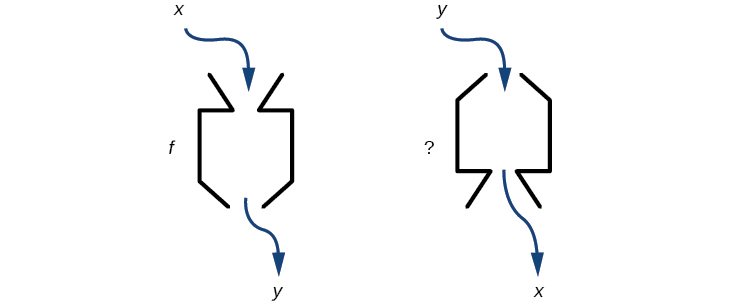
$Mchoro wa kazi na itakuwa inverse yake$
Kielelezo$\PageIndex{1}$: Je, kazi “mashine” kazi katika reverse?

Kuthibitisha kwamba Kazi mbili ni Kazi za Inverse

Tuseme mtengenezaji wa mtindo anayesafiri kwenda Milan kwa show ya mtindo anataka kujua nini joto litakuwa. Yeye hajui na kiwango cha Celsius. Ili kupata wazo la jinsi vipimo vya joto vinavyohusiana, anauliza msaidizi wake, Betty, kubadilisha digrii 75 Fahrenheit hadi digrii Celsius. Yeye hupata formula

\[C=\dfrac{5}{9}(F−32)\]

na substitutes 75 kwa ajili$F$ ya mahesabu

\[\dfrac{5}{9}(75−32)\approx24^{\circ}\]

Kujua kwamba starehe 75 digrii Fahrenheit ni kuhusu 24 digrii Celsius, yeye zituma msaidizi wake wiki ya hali ya hewa ya utabiri kutoka Kielelezo$\PageIndex{2}$ kwa Milan, na kumwomba kubadilisha joto zote kwa digrii Fahrenheit.

Utabiri wa Jumatatu hadi hali ya hewa ya Alhamisi. — Kielelezo$\PageIndex{2}$: utabiri wa Jumatatu kwa njia ya hali ya hewa ya Alhamisi.

Mara ya kwanza, Betty anazingatia kutumia formula ambayo tayari amepata kukamilisha mabadiliko. Baada ya yote, anajua algebra yake, na anaweza kutatua urahisi equation kwa$F$ baada ya kubadilisha thamani kwa$C$. Kwa mfano, kubadili digrii 26 Celsius, angeweza kuandika

\[\begin{align} 26&=\dfrac{5}{9}(F-32) \\ 26⋅\dfrac{9}{5}&=F−32 \\ F&=26⋅\dfrac{9}{5}+32\approx79\end{align}\]

Baada ya kuzingatia chaguo hili kwa muda, hata hivyo, anajua kwamba kutatua equation kwa kila joto itakuwa mbaya sana. Anatambua kwamba tangu tathmini ni rahisi kuliko kutatua, itakuwa rahisi zaidi kuwa na formula tofauti, moja ambayo inachukua joto la Celsius na matokeo ya joto la Fahrenheit.

Fomu ambayo Betty ni kutafuta inalingana na wazo la kazi inverse, ambayo ni kazi ambayo pembejeo ya kazi ya awali inakuwa pato la kazi inverse na pato la kazi ya awali inakuwa pembejeo ya kazi inverse.

Kutokana na kazi$f(x)$, sisi kuwakilisha inverse yake kama$f^{−1}(x)$, kusoma kama “$f$inverse ya$x$.” Mliofufuliwa -1 ni sehemu ya nukuu. Si mtetezi; haimaanishi nguvu ya -1. Kwa maneno mengine,$f^{−1}(x)$ haina maana$\frac{1}{f(x)}$ kwa sababu$\frac{1}{f(x)}$ ni usawa wa$f$ na si inverse.

Nukuu ya “mfano kama” inatokana na mlinganisho kati ya utungaji wa kazi na kuzidisha: kama vile$a^{−1}a=1$ (1 ni kipengele cha utambulisho cha kuzidisha) kwa idadi yoyote isiyo ya sifuri$a$, hivyo ni$f^{−1}{\circ}f$ sawa na kazi ya utambulisho, yaani,

\[(f^{−1}{\circ}f)(x)=f^{−1}(f(x))=f^{−1}(y)=x\]

Hii inashikilia kwa wote$x$ katika uwanja wa$f$. Kwa kawaida, hii ina maana kwamba kazi za inverse “hutenganisha” kila mmoja. Hata hivyo, kama sifuri haina usawa, baadhi ya kazi hazina inverses.

Kutokana na kazi$f(x)$, tunaweza kuthibitisha kama baadhi ya kazi nyingine$g(x)$ ni kinyume cha$f(x)$ kwa kuangalia kama ama$g(f(x))=x$ au$f(g(x))=x$ ni kweli. Tunaweza kupima kwa namna yoyote equation ni rahisi zaidi kufanya kazi na kwa sababu ni kimantiki sawa (yaani, kama moja ni kweli, basi ndivyo ilivyo nyingine.)

Kwa mfano,$y=4x$ na$y=\frac{1}{4}x$ ni kazi inverse.

\[(f^{−1}{\circ}f)(x)=f^{-1}(4x)=\dfrac{1}{4}(4x)=x\]

\[(f{\circ}f^{−1})(x)=f\Big(\dfrac{1}{4}x\Big)=4\Big(\dfrac{1}{4}x\Big)=x\]

Jozi chache za kuratibu kutoka kwenye grafu ya kazi$y=4x$ ni$(−2, −8)$,$(0, 0)$, na$(2, 8)$. Jozi chache za kuratibu kutoka kwenye grafu ya kazi$y=\frac{1}{4}x$ ni$(−8, −2)$,$(0, 0)$, na$(8, 2)$. Kama sisi interchange pembejeo na pato la kila jozi kuratibu ya kazi, interchanged kuratibu jozi itaonekana kwenye grafu ya kazi inverse.

Ufafanuzi: Kazi ya Inverse

Kwa kazi yoyote moja kwa moja$f(x)=y$, kazi$f^{−1}(x)$ ni kazi inverse ya$f$ kama$f^{−1}(y)=x$. Hii pia inaweza kuandikwa kama$f^{−1}(f(x))=x$ kwa wote$x$ katika uwanja wa$f$. Pia ifuatavyo kwamba$f(f^{−1}(x))=x$ kwa wote$x$ katika uwanja wa$f^{−1}$ kama$f^{−1}$ ni inverse ya$f$.

Uthibitisho$f^{−1}$ unasoma “$f$inverse.” Kama kazi nyingine yoyote, tunaweza kutumia jina lolote variable kama pembejeo kwa$f^{−1}$, hivyo sisi mara nyingi kuandika$f^{−1}(x)$, ambayo sisi kusoma kama “$f$inverse ya$x$.” Kumbuka kwamba

\[f^{−1}(x)\neq\dfrac{1}{f(x)}\]

na si kazi zote zina inverses.

Mfano$\PageIndex{1}$: Identifying an Inverse Function for a Given Input-Output Pair

Kama kwa ajili ya kazi fulani moja kwa moja$f(2)=4$ na$f(5)=12$, ni nini sambamba pembejeo na pato maadili kwa ajili ya kazi inverse?

Suluhisho

Kazi inverse reverses kiasi pembejeo na pato, hivyo kama

\[f(2)=4, \text{ then } f^{-1}(4)=2 ;\\ f(5)=12, \text{ then }f^{-1}(12)=5\].

Vinginevyo, kama tunataka jina kazi inverse$g$, basi$g(4)=2$ na$g(12)=5$.

Uchambuzi

Kumbuka kwamba kama sisi kuonyesha jozi kuratibu katika fomu meza, pembejeo na pato ni wazi kuachwa. Angalia Jedwali$\PageIndex{1}$.

Jedwali$\PageIndex{1}$
$(x,f(x))$	$(x,g(x))$
\ (x, f (x))\)” style="wima align:katikati; Nakala-align:katikati; ">$(2,4)$	\ (x, g (x))\)” style="wima align:katikati; Nakala-align:katikati; ">$(4,2)$
\ (x, f (x))\)” style="wima align:katikati; Nakala-align:katikati; ">$(5,12)$	\ (x, g (x))\)” style="wima align:katikati; Nakala-align:katikati; ">$(12,5)$

Zoezi$\PageIndex{1}$

Kutokana na kwamba$h^{-1}(6)=2$, ni maadili gani ya pembejeo na pato la kazi ya awali$h$?

Jibu: $h(2)=6$

Jinsi ya: Kutokana na kazi mbili$f(x)$ and $g(x)$, test whether the functions are inverses of each other.

Kuamua kama$f(g(x))=x$ au$g(f(x))=x$.
Ikiwa taarifa zote mbili ni za kweli, basi$g=f^{-1}$ na$f=g^{-1}$. Ikiwa taarifa yoyote ni ya uongo, basi wote wawili ni uongo,$g{\neq}f^{-1}$ na$f{\neq}g^{-1}$.

Mfano$\PageIndex{2}$: Testing Inverse Relationships Algebraically

Kama$f(x)=\frac{1}{x+2}$ na$g(x)=\frac{1}{x}−2$, ni$g=f^{-1}$?

Suluhisho

\[\begin{align} g(f(x))&=\dfrac{1}{(\frac{1}{x+2})−2} \\ &=x+2−2 \\&=x \end{align}\]

kwa hivyo

\[g=f^{-1} \text{ and } f=g^{-1}\]

Hii ni ya kutosha kujibu ndiyo kwa swali, lakini tunaweza pia kuthibitisha formula nyingine.

\[\begin{align} f(g(x))&=\dfrac{1}{\frac{1}{x}-2+2} \\ &= \dfrac{1}{\frac{1}{x}} \\ &=x \end{align}\]

Uchambuzi

Angalia shughuli inverse ni katika utaratibu wa reverse wa shughuli kutoka kazi ya awali.

Zoezi$\PageIndex{2}$

Kama$f(x)=x^3−4$ na$g(x)=\sqrt[3]{x+4}$, ni$g=f^{-1}$?

Jibu: Ndio

Mfano$\PageIndex{3}$: Determining Inverse Relationships for Power Functions

Kama$f(x)=x^3$ (mchemraba kazi) na$g(x)=\frac{1}{3}x$, ni$g=f^{-1}$?

Suluhisho

\[f(g(x))=\dfrac{x^3}{27}{\neq}x\]

Hapana, kazi sio inverses.
Uchambuzi

Inverse sahihi kwa mchemraba ni, bila shaka, mizizi ya mchemraba$\sqrt[3]{x}=x^{\frac{1}{3}}$, yaani, theluthi moja ni exponent, si multiplier.

Zoezi$\PageIndex{3}$

Kama$f(x)=(x−1)^3$ na$g(x)=\sqrt[3]{x}+1$, ni$g=f^{-1}$?

Jibu: Ndio

Kutafuta Domain na Mipangilio ya Kazi za Inverse

matokeo ya kazi$f$ ni pembejeo kwa$f^{-1}$, hivyo mbalimbali ya pia$f$ ni uwanja wa$f^{-1}$. Vivyo hivyo, kwa sababu pembejeo$f$ ni matokeo ya$f^{-1}$, uwanja wa$f$ ni aina mbalimbali ya$f^{-1}$. Tunaweza taswira hali kama katika Kielelezo$\PageIndex{3}$.

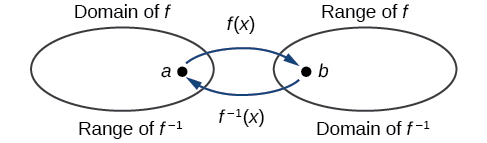
$Domain na mbalimbali ya kazi na inverse yake.$
Kielelezo$\PageIndex{3}$: Domain na mbalimbali ya kazi na inverse yake.

Wakati kazi haina kazi inverse, inawezekana kujenga kazi mpya ambapo kazi mpya kwenye uwanja mdogo haina kazi inverse. Kwa mfano, inverse ya$f(x)=\sqrt{x}$ ni$f^{-1}(x)=x^2$, kwa sababu mraba “huondoa” mizizi ya mraba; lakini mraba ni inverse tu ya mizizi ya mraba kwenye uwanja$\left[0,\infty\right)$, kwa kuwa hiyo ni aina mbalimbali ya$f(x)=\sqrt{x}$.

Tunaweza kuangalia tatizo hili kutoka upande mwingine, kuanzia na kazi ya mraba (toolkit quadratic)$f(x)=x^2$. Kama tunataka kujenga kinyume na kazi hii, sisi kukimbia katika tatizo, kwa sababu kwa kila pato kutokana na kazi quadratic, kuna mbili pembejeo sambamba (isipokuwa wakati pembejeo ni 0). Kwa mfano, pato 9 kutoka kazi ya quadratic inalingana na pembejeo 3 na -3. Lakini pato kutoka kwa kazi ni pembejeo kwa inverse yake; ikiwa pembejeo hii inverse inalingana na pato zaidi ya moja inverse (pembejeo ya kazi ya awali), basi “inverse” sio kazi kabisa! Ili kuiweka tofauti, kazi ya quadratic sio kazi moja kwa moja; inashindwa mtihani wa mstari wa usawa, kwa hiyo haina kazi ya inverse. Ili kazi iwe na inverse, lazima iwe kazi moja kwa moja.

Mara nyingi, kama kazi si moja kwa moja, bado tunaweza kuzuia kazi kwa sehemu ya uwanja wake ambayo ni moja kwa moja. Kwa mfano, tunaweza kufanya toleo la vikwazo la kazi ya mraba$f(x)=x^2$ na upeo wake mdogo$\left[0,\infty\right)$, ambayo ni kazi moja kwa moja (inapita mtihani wa mstari wa usawa) na ambayo ina inverse (kazi ya mizizi ya mraba).

Ikiwa$f(x)=(x−1)^2$ juu$[1,∞)$, basi kazi ya inverse ni$f^{-1}(x)=\sqrt{x}+1$.

uwanja wa$f$ = mbalimbali ya$f^{-1} = \left[1,\infty\right)$.
uwanja wa$f^{-1}$ = mbalimbali ya$f = \left[0,\infty\right)$.

$alt$ Je, inawezekana kwa kazi kuwa na inverse zaidi ya moja?

Hapana. Ikiwa kazi mbili zinadaiwa tofauti, sema,$g$ na h, wote hukutana na ufafanuzi wa kuwa inverses ya kazi nyingine$f$, basi unaweza kuthibitisha hilo$g=h$. Tumeona tu kwamba baadhi ya kazi tu inverses kama sisi kuzuia uwanja wa kazi ya awali. Katika kesi hizi, kunaweza kuwa na njia zaidi ya moja ya kuzuia kikoa, na kusababisha inverses tofauti. Hata hivyo, kwenye uwanja wowote, kazi ya awali bado ina inverse moja tu ya kipekee.

Kumbuka: Domain na Mipangilio ya Kazi za Inverse

Kazi mbalimbali$f(x)$ ni uwanja wa kazi ya inverse$f^{-1}(x)$.

uwanja wa$f(x)$ ni mbalimbali ya$f^{-1}(x)$.

Jinsi ya: Kutokana na kazi, tafuta kikoa na upeo wa inverse yake.

Ikiwa kazi ni moja kwa moja, weka aina mbalimbali ya kazi ya awali kama uwanja wa inverse, na uandike kikoa cha kazi ya awali kama upeo wa inverse.
Ikiwa uwanja wa kazi ya awali unahitaji kuzuiwa ili kuifanya moja kwa moja, basi uwanja huu uliozuiliwa unakuwa kazi ya inverse.

Mfano$\PageIndex{4}$: Finding the Inverses of Toolkit Functions

Tambua ni kazi gani ya toolkit badala ya kazi ya quadratic sio moja kwa moja, na kupata kikoa kilichozuiliwa ambacho kila kazi ni moja kwa moja, ikiwa ipo. Kazi za toolkit zinarekebishwa katika Jedwali$\PageIndex{2}$. Sisi kuzuia uwanja kwa namna hiyo kwamba kazi inachukua kila y-maadili hasa mara moja.

Jedwali$\PageIndex{2}$
Mara kwa mara	Identity	Quadratic	Cubic	kurudisha nyuma
$f(x)=c$	$f(x)=x$	$f(x)=x^2$	$f(x)=x^3$	$f(x)=\frac{1}{x}$
Mraba ya kurudisha	mchemraba mzizi	Mizizi ya mraba	Thamani kamili
$f(x)=\frac{1}{x^2}$	$f(x)=\sqrt[3]{x}$	$f(x)=\sqrt{x}$	$f(x)=\|x\|$

Suluhisho

Kazi ya mara kwa mara sio moja kwa moja, na hakuna uwanja (isipokuwa hatua moja) ambayo inaweza kuwa moja kwa moja, hivyo kazi ya mara kwa mara haina inverse ya maana.

Kazi ya thamani kamili inaweza kuzuiwa kwenye uwanja$\left[0,\infty\right)$, ambapo ni sawa na kazi ya utambulisho.

Kazi ya mraba ya usawa inaweza kuzuiwa kwenye kikoa$(0,\infty)$.

Uchambuzi

Tunaweza kuona kwamba kazi hizi (ikiwa hazipatikani) sio moja kwa moja kwa kuangalia grafu zao, zilizoonyeshwa kwenye Kielelezo$\PageIndex{4}$. Wote wawili bila kushindwa usawa line mtihani. Hata hivyo, ikiwa kazi imezuiwa kwenye uwanja fulani ili iweze kupima mtihani wa mstari usio na usawa, basi katika uwanja huo uliozuiliwa, inaweza kuwa na inverse.

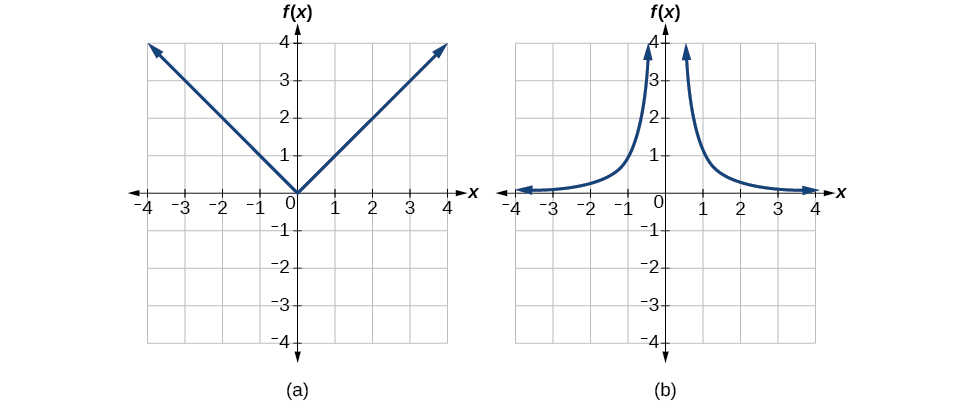
$Grafu ya kazi kamili.$
Kielelezo$\PageIndex{4}$: (a) Thamani kamili (b) Mraba ya usawa

$alt$ $\PageIndex{4}$: uwanja wa kazi$f$ ni$(1,\infty)$ na aina mbalimbali ya kazi$f$ ni$(−\infty,−2)$. Pata kikoa na upeo wa kazi ya inverse.

Suluhisho

Kikoa cha kazi$f^{-1}$ ni$(−\infty,−2)$ na kazi mbalimbali$f^{-1}$ ni$(1,\infty)$.

Kutafuta na Kutathmini Kazi za Inverse

Mara baada ya kuwa na kazi moja kwa moja, tunaweza kutathmini inverse yake katika pembejeo maalum inverse kazi au kujenga uwakilishi kamili wa kazi inverse katika kesi nyingi.

Inverting Tabular Kazi

Tuseme tunataka kupata inverse ya kazi iliyowakilishwa katika fomu ya meza. Kumbuka kwamba uwanja wa kazi ni aina mbalimbali ya inverse na aina mbalimbali ya kazi ni uwanja wa inverse. Kwa hiyo tunahitaji kubadilishana kikoa na upeo.

Kila mstari (au safu) ya pembejeo inakuwa mstari (au safu) ya matokeo kwa kazi ya inverse. Vile vile, kila mstari (au safu) ya matokeo inakuwa mstari (au safu) ya pembejeo kwa kazi ya inverse.

Mfano$\PageIndex{5}$: Interpreting the Inverse of a Tabular Function

Kazi$f(t)$ imetolewa katika Jedwali$\PageIndex{3}$, kuonyesha umbali katika maili kwamba gari ina alisafiri katika$t$ dakika. Pata na kutafsiri$f^{-1}(70)$

Jedwali$\PageIndex{3}$
$t$(dakika)	30	50	70	90
$f(t)$(maili)	20	40	60	70

kazi inverse inachukua pato la$f$ na anarudi pembejeo kwa$f$. Hivyo katika kujieleza$f^{-1}(70)$, 70 ni thamani pato la kazi ya awali, anayewakilisha 70 maili. Inverse itarudi pembejeo inayofanana ya kazi ya awali$f$, dakika 90, hivyo$f^{-1}(70)=90$. Tafsiri ya hii ni kwamba, kuendesha maili 70, ilichukua dakika 90.

Vinginevyo, kumbuka kwamba ufafanuzi wa inverse ni kwamba kama$f(a)=b$, basi$f^{-1}(b)=a$. Kwa ufafanuzi huu, ikiwa tunapewa$f^{-1}(70)=a$, basi tunatafuta thamani$a$ ili$f(a)=70$. Katika hali hii, sisi ni kuangalia kwa$t$ ili$f(t)=70$, ambayo ni wakati$t=90$.

Zoezi$\PageIndex{5}$

Kutumia Jedwali$\PageIndex{4}$, tafuta na kutafsiri (a)$f(60)$, na (b)$f^{-1}(60)$.

Jedwali$\PageIndex{4}$
$t$(dakika)	30	50	60	70	90
$f(t)$(maili)	20	40	50	60	70

Jibu: $f(60)=50$. Katika dakika 60, maili 50 zinasafiri.
$f^{-1}(60)=70$. Ili kusafiri maili 60, itachukua dakika 70.

Kutathmini Inverse ya Kazi, Kutokana na Grafu ya Kazi ya Awali

Tuliona katika Kazi na Uthibitishaji wa Kazi kwamba uwanja wa kazi unaweza kusoma kwa kuchunguza kiwango cha usawa cha grafu yake. Tunapata uwanja wa kazi ya inverse kwa kuchunguza kiwango cha wima cha grafu ya kazi ya awali, kwa sababu hii inalingana na kiwango cha usawa cha kazi ya inverse. Vile vile, tunapata kazi mbalimbali ya inverse kwa kuchunguza kiwango cha usawa cha grafu ya kazi ya awali, kwa kuwa hii ni kiwango cha wima cha kazi ya inverse. Ikiwa tunataka kutathmini kazi inverse, tunapata pembejeo yake ndani ya uwanja wake, ambayo ni yote au sehemu ya mhimili wima wa grafu ya kazi ya awali.

$alt$ Kutokana na grafu ya kazi, tathmini inverse yake katika pointi maalum.

Pata pembejeo inayotakiwa kwenye mhimili wa y wa grafu iliyotolewa.
Soma pato la kazi ya inverse kutoka kwenye mhimili wa x-wa grafu iliyotolewa.

Mfano$\PageIndex{6}$: Evaluating a Function and Its Inverse from a Graph at Specific Points

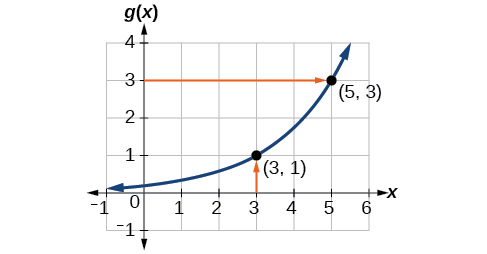
Kazi$g(x)$ hutolewa katika Kielelezo$\PageIndex{5}$. Kupata$g(3)$ na$g^{-1}(3)$.
.

Grafu ya <span tafsiri = — Kielelezo$\PageIndex{5}$: Grafu ya$g(x)$

Suluhisho

Ili kutathmini$g(3)$, tunapata 3 kwenye mhimili wa x na kupata thamani ya pato inayofanana kwenye mhimili wa y. Hatua$(3,1)$ inatuambia kwamba$g(3)=1$.

Kutathmini$g^{-1}(3)$, kukumbuka kwamba kwa ufafanuzi$g^{-1}(3)$ ina maana thamani$x$ ya ambayo$g(x)=3$. Kwa kuangalia thamani ya pato 3 kwenye mhimili wima, tunapata uhakika$(5,3)$ kwenye grafu, ambayo ina maana$g(5)=3$, kwa ufafanuzi,$g^{-1}(3)=5.$ Angalia Mchoro$\PageIndex{6}$.

grafu ya g (x) — Kielelezo$\PageIndex{6}$: Grafu ya$g(x)$.

Zoezi$\PageIndex{6}$

Kutumia grafu katika Kielelezo$\PageIndex{6}$, (a) kupata$g^{-1}(1)$, na (b) makadirio$g^{-1}(4)$.

Jibu: 3
Jibu b: 5.6

Kutafuta Inverses ya Kazi Inawakilishwa na Fomu

Wakati mwingine tutahitaji kujua kazi ya inverse kwa vipengele vyote vya uwanja wake, sio wachache tu. Kama kazi ya awali ni kutolewa kama formula - kwa mfano,$y$ kama kazi ya$x$ - tunaweza mara nyingi kupata kazi inverse na kutatua kupata$x$ kama kazi ya$y$.

Jinsi ya: Kutokana na kazi iliyowakilishwa na formula, tafuta inverse.

Hakikisha$f$ ni kazi moja kwa moja.
Kutatua kwa$x$
$x$Kubadilishana na$y$.

Mfano$\PageIndex{7}$: Inverting the Fahrenheit-to-Celsius Function

Kupata formula kwa ajili ya kazi inverse ambayo inatoa Fahrenheit joto kama kazi ya joto Celsius.

\[C=\dfrac{5}{9}(F−32)\]

Suluhisho

\[\begin{align} C&=\frac{5}{9}(F-32) \\ C{\cdot}\frac{9}{5}&=F−32 \\ F&=\frac{9}{5}C+32\end{align}\]

Kwa kutatua kwa ujumla, tumefunua kazi ya inverse. Kama

\[C=h(F)=\dfrac{5}{9}(F−32)\],

basi

\[F=h^{-1}(C)=\dfrac{9}{5}C+32.\]

Katika kesi hiyo, sisi ilianzisha kazi ya$h$ kuwakilisha uongofu kwa sababu vigezo pembejeo na pato ni maelezo, na kuandika$C^{-1}$ inaweza kupata utata.

Zoezi$\PageIndex{7}$

Kutatua kwa$x$ katika suala la$y$ kupewa$y=\frac{1}{3}(x−5)$

Jibu: $x=3y+5$

Mfano$\PageIndex{8}$: Solving to Find an Inverse Function

Pata inverse ya kazi$f(x)=\frac{2}{x−3}+4$.

Suluhisho

\[\begin{align} y&=\dfrac{2}{x−3+4} &\text{Set up an equation.} \\ y−4&=\dfrac{2}{x−3} &\text{Subtract 4 from both sides.} \\ x−3&=\dfrac{2}{y−4} &\text{Multiply both sides by x−3 and divide by y−4.} \\ x&=\dfrac{2}{y−4}+3 &\text{Add 3 to both sides.} \end{align}\]

Hivyo$f^{-1}(y)=\frac{2}{y−4}+3$ au$f^{-1}(x)=\frac{2}{x−4}+3$.

Uchambuzi

Domain na aina mbalimbali ya$f$ kuwatenga maadili 3 na 4, kwa mtiririko huo. $f$na$f^{-1}$ ni sawa katika pointi mbili lakini si kazi sawa, kama tunaweza kuona kwa kujenga Jedwali$\PageIndex{5}$.

Jedwali$\PageIndex{5}$
$x$	1	2	5	$f^{-1}(y)$
$f(x)$	3	2	5	$y$

Mfano$\PageIndex{9}$: Solving to Find an Inverse with Radicals

Pata inverse ya kazi$f(x)=2+\sqrt{x−4}$.

Suluhisho

\[ \begin{align} y&=2+\sqrt{x-4} \\ (y-2)^2&=x-4 \\ x&=(y-2)^2+4 \end{align}\]

Hivyo$f^{-1}(x)=(x−2)^2+4$.

uwanja wa$f$ ni$\left[4,\infty\right)$. Kumbuka kwamba mbalimbali ya$f$ ni$\left[2,\infty\right)$, hivyo hii ina maana kwamba uwanja wa kazi$f^{-1}$ inverse pia$\left[2,\infty\right)$

Uchambuzi

formula sisi kupatikana kwa$f^{-1}(x)$ inaonekana kama itakuwa halali kwa wote halisi$x$. Hata hivyo,$f^{-1}$ yenyewe lazima iwe na inverse (yaani,$f$) hivyo tunapaswa kuzuia uwanja wa$\left[2,\infty\right)$ kwa$f^{-1}$ ili kufanya kazi moja$f^{-1}$ kwa moja. Uwanja huu wa$f^{-1}$ ni hasa mbalimbali ya$f$.

Zoezi$\PageIndex{8}$

Je, ni inverse ya kazi gani$f(x)=2-\sqrt{x}$? Weka vikoa vya kazi zote mbili na kazi ya inverse.

Jibu: $f^{-1}(x)=(2−x)^2$; uwanja wa$f$:$\left[0,\infty\right)$; uwanja wa$f^{-1}$:$\left(−\infty,2\right]$

Kutafuta Kazi za Inverse na Grafu zao

Sasa kwa kuwa tunaweza kupata inverse ya kazi, sisi kuchunguza grafu ya kazi na inverses yao. Hebu kurudi kwenye kazi ya quadratic$f(x)=x^2$ iliyozuiliwa kwenye uwanja$\left[0,\infty\right)$, ambayo kazi hii ni moja kwa moja, na kuiweka kama kwenye Mchoro$\PageIndex{7}$.

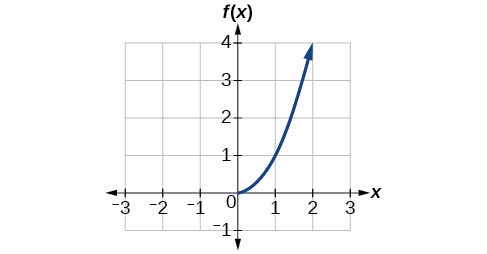
$Grafu ya f (x).$
Kielelezo$\PageIndex{7}$: Quadratic kazi na uwanja vikwazo kwa$[0, \infty)$.

Kuzuia kikoa$\left[0,\infty\right)$ kufanya kazi moja kwa moja (itakuwa wazi kupitisha mtihani wa mstari usio na usawa), kwa hiyo ina inverse kwenye uwanja huu uliozuiliwa.

Tayari tunajua kwamba inverse ya kazi ya quadratic ya toolkit ni kazi ya mizizi ya mraba, yaani,$f^{-1}(x)=\sqrt{x}$. Nini kinatokea ikiwa tunapiga picha zote mbili$f$ na$f^{-1}$ kwenye seti sawa ya axes, kwa kutumia x-axis kwa pembejeo kwa wote$f$ na$f^{-1}$?

Tunaona uhusiano tofauti: Grafu ya$f^{-1}(x)$ ni grafu ya$f(x)$ yalijitokeza juu ya mstari wa diagonal$y=x$, ambayo tutaita mstari wa utambulisho, umeonyeshwa kwenye Mchoro$\PageIndex{8}$.

\ (f (x)\) na$f^(-1)(x)$. "src=” https://math.libretexts.org/@api/dek..._01_07_009.jpg "/>.
Kielelezo$\PageIndex{8}$: Kazi za mraba na za mraba kwenye uwanja usio na hasi

Uhusiano huu utazingatiwa kwa kazi zote moja kwa moja, kwa sababu ni matokeo ya kazi na pembejeo zake za kuingiliana na matokeo. Hii ni sawa na kubadilishana majukumu ya axes wima na usawa.

Mfano$\PageIndex{10}$: Finding the Inverse of a Function Using Reflection about the Identity Line

Kutokana na grafu ya$f(x)$ katika Kielelezo$\PageIndex{9}$, mchoro grafu ya$f^{-1}(x)$.

Hii ni kazi moja kwa moja, kwa hiyo tutaweza kuchora inverse. Kumbuka kuwa grafu inavyoonekana ina uwanja dhahiri wa$(0,\infty)$ na mbalimbali ya$(−\infty,\infty)$, hivyo inverse itakuwa na uwanja wa$(−\infty,\infty)$ na mbalimbali ya$(0,\infty)$.

Ikiwa tunaonyesha grafu hii juu ya mstari$y=x$, hatua$(1,0)$ inaonyesha$(0,1)$ na uhakika$(4,2)$ unaonyesha$(2,4)$. Sketching inverse juu ya axes sawa na grafu ya awali anatoa Kielelezo$\PageIndex{10}$.

Zoezi$\PageIndex{1}$

Chora grafu ya kazi$f$ na$f^{-1}$ kutoka Mfano$\PageIndex{8}$.

Jibu: \ (f (x)\) na$f^(-1)(x)$.” src=” https://math.libretexts.org/@api/dek..._01_07_012.jpg "/>
Kielelezo$\PageIndex{11}$: Grafu ya$f(x)$ na$f^(-1)(x)$.

$alt$ Je, kuna kazi yoyote ambayo ni sawa na inverse yake mwenyewe?

Ndiyo. Ikiwa$f=f^{-1}$, basi$f(f(x))=x$, na tunaweza kufikiria kazi kadhaa ambazo zina mali hii. Kazi ya utambulisho

gani, na hivyo kazi ya kurudi, kwa sababu

\[\dfrac{1}{\frac{1}{x}}=x\]

Kazi yoyote$f(x)=c−x$, ambapo$c$ ni mara kwa mara, pia ni sawa na inverse yake mwenyewe.

Dhana muhimu

Kama$g(x)$ ni inverse ya$f(x)$, basi$g(f(x))=f(g(x))=x$.
Kila moja ya kazi ya toolkit ina inverse.
Kwa kazi kuwa na inverse, lazima iwe moja kwa moja (kupitisha mtihani wa mstari usio na usawa).
Kazi ambayo si moja kwa moja juu ya uwanja wake wote inaweza kuwa moja kwa moja kwa sehemu ya uwanja wake.
Kwa kazi ya tabular, ubadilishane safu za pembejeo na pato ili kupata inverse.
Inverse ya kazi inaweza kuamua kwa pointi maalum kwenye grafu yake.
Ili kupata inverse ya formula, kutatua equation$y=f(x)$ kwa$x$ kama kazi ya$y$. Kisha kubadilishana maandiko$x$ na$y$.
Grafu ya kazi ya inverse ni kutafakari kwa grafu ya kazi ya awali kwenye mstari$y=x$.

\((x,f(x))\)	\((x,g(x))\)
\ (x, f (x))\)” style="wima align:katikati; Nakala-align:katikati; ">\((2,4)\)	\ (x, g (x))\)” style="wima align:katikati; Nakala-align:katikati; ">\((4,2)\)
\ (x, f (x))\)” style="wima align:katikati; Nakala-align:katikati; ">\((5,12)\)	\ (x, g (x))\)” style="wima align:katikati; Nakala-align:katikati; ">\((12,5)\)

\(x\)	1	2	5	\(f^{-1}(y)\)
\(f(x)\)	3	2	5	\(y\)

Mara kwa mara	Identity	Quadratic	Cubic	kurudisha nyuma
\(f(x)=c\)	\(f(x)=x\)	\(f(x)=x^2\)	\(f(x)=x^3\)	\(f(x)=\frac{1}{x}\)
Mraba ya kurudisha	mchemraba mzizi	Mizizi ya mraba	Thamani kamili
\(f(x)=\frac{1}{x^2}\)	\(f(x)=\sqrt[3]{x}\)	\(f(x)=\sqrt{x}\)	\(f(x)=\|x\|\)

Jedwali\(\PageIndex{3}\)
\(t\)(dakika)	30	50	70	90
\(f(t)\)(maili)	20	40	60	70

Jedwali\(\PageIndex{4}\)
\(t\)(dakika)	30	50	60	70	90
\(f(t)\)(maili)	20	40	50	60	70