1.4: Muundo wa Kazi

Malengo ya kujifunza

• Kuchanganya kazi kwa kutumia shughuli za algebraic.
• Unda kazi mpya kwa muundo wa kazi.
• Tathmini kazi za Composite.
• Pata uwanja wa kazi ya composite.
• Punguza kazi ya composite katika kazi zake za sehemu.

Tuseme tunataka kuhesabu ni kiasi gani kinachohitajika kwa joto la nyumba siku fulani ya mwaka. Gharama ya joto nyumba itategemea wastani wa joto la kila siku, na kwa upande mwingine, wastani wa joto la kila siku hutegemea siku fulani ya mwaka. Angalia jinsi tulivyofafanua mahusiano mawili: gharama inategemea joto, na joto hutegemea siku.

Kutumia vigezo maelezo, tunaweza notate kazi hizi mbili. Kazi$C(T)$ hutoa gharama ya$C$ kupokanzwa nyumba kwa wastani wa joto la kila siku katika$T$ digrii Celsius. Kazi$T(d)$ hutoa wastani wa joto la kila siku siku d ya mwaka. Kwa siku yoyote,$Cost=C(T(d))$ ina maana kwamba gharama inategemea joto, ambalo linategemea siku ya mwaka. Hivyo, tunaweza kutathmini kazi ya gharama kwenye joto$T(d)$. Kwa mfano, tunaweza$T(5)$ kutathmini kuamua wastani wa joto la kila siku siku ya 5 ya mwaka. Kisha, tunaweza kutathmini kazi ya gharama katika joto hilo. Tunataka kuandika$C(T(5))$.

Kielelezo$\PageIndex{1}$: Maelezo ya$C(T(5))$, ambayo ni gharama ya joto na$T(5)$ ni joto siku 5.

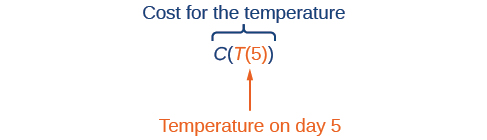
Kwa kuchanganya mahusiano haya mawili katika kazi moja, tumefanya utungaji wa kazi, ambayo ni lengo la sehemu hii.

Kuchanganya Kazi Kutumia Operesheni za Algebraic

Utungaji wa kazi ni njia moja tu ya kuchanganya kazi zilizopo. Njia nyingine ni kutekeleza shughuli za kawaida za algebraic juu ya kazi, kama vile kuongeza, kuondoa, kuzidisha na mgawanyiko. Tunafanya hivyo kwa kufanya shughuli na matokeo ya kazi, kufafanua matokeo kama pato la kazi yetu mpya.

Tuseme tunahitaji kuongeza nguzo mbili za namba zinazowakilisha mapato ya kila mwaka ya mume na mke kwa kipindi cha miaka, na matokeo yake ni jumla ya mapato ya kaya. Tunataka kufanya hivyo kwa kila mwaka, na kuongeza tu mapato ya mwaka huo na kisha kukusanya data zote katika safu mpya. Ikiwa$w(y)$ ni mapato ya mke na$h(y)$ ni mapato ya mume kwa mwaka$y$, na tunataka$T$ kuwakilisha mapato ya jumla, basi tunaweza kufafanua kazi mpya.

$$T(y)=h(y)+w(y) \nonumber$$

Ikiwa hii inashikilia kwa kila mwaka, basi tunaweza kuzingatia uhusiano kati ya kazi bila kutaja mwaka na kuandika

$$T=h+w \nonumber$$

Kama vile kwa jumla hii ya kazi mbili, tunaweza kufafanua tofauti, bidhaa, na uwiano kazi kwa jozi yoyote ya kazi ambayo aina moja ya pembejeo (si lazima idadi) na pia aina hiyo ya matokeo (ambayo kufanya kuwa idadi ili shughuli ya kawaida ya algebra inaweza kuomba kwao, na ambayo pia lazima uwe na vitengo sawa au hakuna vitengo wakati sisi kuongeza na Ondoa). Kwa njia hii, tunaweza kufikiria kuongeza, kuondoa, kuzidisha, na kugawa kazi.

Kwa kazi mbili$f(x)$$g(x)$ na kwa matokeo halisi ya idadi, tunafafanua kazi mpya$f+g$$f−g$,$fg$, na$\frac{f}{g}$ kwa mahusiano.

$$\begin{align*} (f+g)(x) &=f(x)+g(x) \\[4pt] (f−g)(x) &=f(x)−g(x) \\[4pt] (fg)(x)&=f(x)g(x) \\[4pt] \left(\dfrac{f}{g}\right)(x) &=\dfrac{f(x)}{g(x)} \end{align*}$$

Mfano$\PageIndex{1}$: Performing Algebraic Operations on Functions

Kupata na kurahisisha kazi$(g−f)(x)$ na$\left(\dfrac{g}{f}\right)(x)$, kutokana$f(x)=x−1$ na$g(x)=x^2−1$. Je, wao ni kazi sawa?

Suluhisho

Anza kwa kuandika fomu ya jumla, na kisha ubadilishe kazi zilizopewa.

$$\begin{align*} (g−f)(x) &= g(x)−f(x) \\[4pt] (g−f)(x) &=x^2−1−(x−1) \\[4pt] &=x^2−x \\[4pt] &=x(x−1) \end{align*}$$

$$\begin{align*} \left(\dfrac{g}{f}\right)(x)&=g(x)f(x) \\[4pt] \left(\dfrac{g}{f}\right)(x)&=\dfrac{x^2−1}{x−1} \\[4pt] &=\dfrac{(x+1)(x−1)}{x−1} \\[4pt]&=x+1 \end{align*}$$

Hapana, kazi si sawa.

Kumbuka: Kwa$\left(\dfrac{g}{f}\right)(x)$, hali$x\neq1$ ni muhimu kwa sababu wakati$x=1$, denominator ni sawa na 0, ambayo inafanya kazi isiyojulikana.

Zoezi$\PageIndex{1}$

Kupata na kurahisisha kazi$(fg)(x)$ na$(f−g)(x)$.

$$f(x)=x−1 \nonumber$$

na

$$g(x)=x^2−1 \nonumber$$

Je, wao ni kazi sawa?

Jibu

$(fg)(x)=f(x)g(x)=(x−1)(x2−1)=x^3−x^2−x+1 \\[4pt] (f−g)(x)=f(x)−g(x)=(x−1)−(x^2−1)=x−x^2$

Hapana, kazi si sawa.

Unda Kazi kwa Muundo wa Kazi

Kufanya shughuli za algebraic kwenye kazi huwachanganya kuwa kazi mpya, lakini tunaweza pia kuunda kazi kwa kutunga kazi. Tulipotaka kukokotoa gharama inapokanzwa kutoka siku ya mwaka, tuliunda kazi mpya ambayo inachukua siku kama pembejeo na hutoa gharama kama pato. Mchakato wa kuchanganya kazi ili pato la kazi moja iwe pembejeo ya mwingine inajulikana kama muundo wa kazi. Kazi inayojulikana inajulikana kama kazi ya composite. Tunawakilisha mchanganyiko huu kwa maelezo yafuatayo:

$$f{\circ}g(x)=f(g(x))$$

Tunasoma upande wa kushoto kama “$f$linajumuisha$g$ saa$x$,” na upande wa kulia kama “$f$$g$ya$x$.” pande mbili za equation zina maana sawa ya hisabati na ni sawa. Ishara ya mduara wazi$\circ$ inaitwa operator wa utungaji. Tunatumia operator hii hasa wakati tunataka kusisitiza uhusiano kati ya kazi wenyewe bila kutaja thamani yoyote ya pembejeo. Muundo ni operesheni ya binary ambayo inachukua kazi mbili na hufanya kazi mpya, kama vile kuongeza au kuzidisha inachukua namba mbili na inatoa idadi mpya. Hata hivyo, ni muhimu kutochanganya utungaji wa kazi na kuzidisha kwa sababu, kama tulivyojifunza hapo juu, mara nyingi$f(g(x)){\neq}f(x)g(x)$.

Pia ni muhimu kuelewa utaratibu wa shughuli katika kutathmini kazi ya composite. Tunafuata mkataba wa kawaida na mabano kwa kuanzia na mabano ya ndani ya kwanza, na kisha kufanya kazi kwa nje. Katika equation hapo juu, kazi$g$ inachukua pembejeo$x$ kwanza na hutoa pato$g(x)$. Kisha kazi$f$ inachukua$g(x)$ kama pembejeo na hutoa pato$f(g(x))$.

Kielelezo$\PageIndex{2}$: Maelezo ya kazi ya composite.

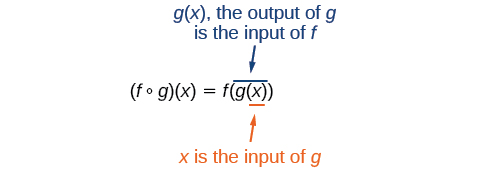
Kwa ujumla,$f{\circ}g$ na$g{\circ}f$ ni kazi tofauti. Kwa maneno mengine, katika hali nyingi$f(g(x)){\neq}g(f(x))$ kwa wote$x$. Tutaona pia kwamba wakati mwingine kazi mbili zinaweza kuundwa tu kwa utaratibu mmoja maalum.

Kwa mfano, ikiwa$f(x)=x^2$ na$g(x)=x+2$, basi

$$\begin{align*} f(g(x))&= f(x+2) \\[4pt]&=(x+2)^2 \\[4pt] &=x^2+4x+4 \end{align*}$$

lakini

$$\begin{align*} g(f(x))&= g(x^2) \\[4pt]&=x^2+2 \end{align*}$$

Maneno haya si sawa kwa maadili yote ya x, hivyo kazi mbili si sawa. Sio maana kwamba maneno yanatokea kuwa sawa kwa thamani moja ya pembejeo$x=−\frac{1}{2}$.

Kumbuka kuwa kazi ya ndani (kazi ya kwanza ya kupimwa) inahitaji kuwa ndani ya uwanja wa kazi ya nje. Chini rasmi, muundo una maana katika suala la pembejeo na matokeo.

Muundo wa Kazi

Wakati pato la kazi moja linatumiwa kama pembejeo ya mwingine, tunaita operesheni nzima muundo wa kazi. Kwa pembejeo yoyote$x$ na kazi$f$ na$g$, hatua hii inafafanua kazi Composite, ambayo sisi kuandika kama$f{\circ}g$ vile kwamba

$$(f{\circ}g)(x)=f(g(x))$$

Kikoa cha kazi ya composite$f{\circ}g$$x$ ni yote$x$ yaliyo katika uwanja wa$g$ na$g(x)$ iko katika uwanja wa$f$.

Ni muhimu kutambua kwamba bidhaa za kazi$fg$ si sawa na utungaji wa kazi$f(g(x))$, kwa sababu, kwa ujumla,$f(x)g(x){\neq}f(g(x))$.

Mfano$\PageIndex{2}$: Determining whether Composition of Functions is Commutative

Kutumia kazi zinazotolewa,$f(g(x))$ tafuta na$g(f(x))$. Kuamua kama muundo wa kazi ni commutative.

$$f(x)=2x+1 \;\;\;\; g(x)=3−x \nonumber$$

Suluhisho

Hebu tuanze kwa kubadili$g(x)$ ndani$f(x)$.

$$\begin{align*} f(g(x))&= 2(3−x)+1 \\[4pt] &=6−2x+1 \\[4pt] &=7−2x \end{align*}$$

Sasa tunaweza mbadala$f(x)$ katika$g(x)$.

$$\begin{align*} g(f(x))&= 3−(2x+1) \\[4pt]&=3−2x−1 \\[4pt] &=2-2x \end{align*}$$

Tunaona kwamba$g(f(x)){\neq}f(g(x))$, hivyo uendeshaji wa utungaji wa kazi sio kubadilisha.

Mfano$\PageIndex{3}$: Interpreting Composite Functions

Kazi$c(s)$ hutoa idadi ya kalori kuchomwa moto kukamilisha$s$ kukaa, na$s(t)$ hutoa idadi ya kukaa mtu anaweza kukamilisha kwa$t$ dakika. Tafsiri$c(s(3))$.

Suluhisho

Maneno ya ndani katika muundo ni$s(3)$. Kwa sababu pembejeo ya$s$ -kazi ni wakati,$t=3$ inawakilisha 3 dakika, na$s(3)$ ni idadi ya kukaa-ups kukamilika katika 3 dakika.

Kutumia$s(3)$ kama pembejeo kwa kazi$c(s)$ inatupa idadi ya kalori kuchomwa wakati wa idadi ya kukaa-ups ambayo inaweza kukamilika kwa dakika 3, au tu idadi ya kalori kuchomwa moto katika dakika 3 (kwa kufanya kukaa-ups).

Mfano$\PageIndex{4}$: Investigating the Order of Function Composition

Tuseme$f(x)$ anatoa maili ambayo inaweza inaendeshwa katika$x$ masaa na$g(y)$ anatoa galoni ya gesi kutumika katika kuendesha$y$ maili. Ni ipi kati ya maneno haya yenye maana:$f(g(y))$ au$g(f(x))$?

Suluhisho

Kazi$y=f(x)$ ni kazi ambao pato ni idadi ya maili inaendeshwa sambamba na idadi ya masaa inaendeshwa.

$$\text{number of miles } =f (\text{number of hours}) \nonumber$$

Kazi$g(y)$ ni kazi ambayo pato lake ni idadi ya galoni zinazotumiwa sambamba na idadi ya maili inayotokana. Hii ina maana:

$$\text{number of gallons } =g(\text{number of miles}) \nonumber$$

$g(y)$usemi inachukua maili kama pembejeo na idadi ya galoni kama pato. Kazi$f(x)$ inahitaji masaa kadhaa kama pembejeo. Kujaribu kuingiza idadi ya galoni haina maana. Maneno$f(g(y))$ haya hayana maana.

usemi$f(x)$ inachukua masaa kama pembejeo na idadi ya maili inaendeshwa kama pato. kazi$g(y)$ inahitaji idadi ya maili kama pembejeo. kutumia$f(x)$ (maili inaendeshwa) kama thamani pembejeo kwa$g(y)$, ambapo galoni ya gesi inategemea maili inaendeshwa, haina mantiki. Maneno$g(f(x))$ yana maana, na itazaa idadi ya galoni za gesi kutumika$g$, kuendesha gari idadi fulani ya maili$f(x)$, katika$x$ masaa.

Swali/Jibu

Je, kuna hali yoyote ambapo$f(g(y))$ na$g(f(x))$ ingekuwa maneno yenye maana au muhimu?

Ndiyo. Kwa kazi nyingi za hisabati safi, nyimbo zote mbili zina maana, ingawa kwa kawaida huzalisha kazi mpya tofauti. Katika matatizo halisi ya ulimwengu, kazi ambazo pembejeo na matokeo zina vitengo sawa pia vinaweza kutoa nyimbo ambazo zina maana katika utaratibu wowote.

Zoezi$\PageIndex{2}$

Nguvu ya mvuto kwenye sayari umbali$r$ kutoka jua hutolewa na kazi$G(r)$. Kuongezeka kwa sayari inakabiliwa na nguvu yoyote$F$ hutolewa na kazi$a(F)$. Fanya muundo wa maana wa kazi hizi mbili, na ueleze maana yake.

Jibu

Nguvu ya mvuto bado ni nguvu, hivyo huwa na$a(G(r))$ maana kama kasi ya sayari kwa umbali$r$ kutoka Jua (kutokana na mvuto), lakini$G(a(F))$ haina maana.

Kutathmini Kazi Composite

Mara tu sisi kutunga kazi mpya kutoka kazi mbili zilizopo, tunahitaji kuwa na uwezo wa kutathmini kwa pembejeo yoyote katika uwanja wake. Sisi kufanya hivyo kwa pembejeo maalum namba kwa ajili ya kazi walionyesha kama meza, grafu, na formula na kwa vigezo kama pembejeo kwa kazi walionyesha kama formula. Katika kila kesi, tunatathmini kazi ya ndani kwa kutumia pembejeo ya kuanzia na kisha kutumia pato la kazi ya ndani kama pembejeo kwa kazi ya nje.

Kutathmini Kazi za Composite Kutumia Meza

Wakati wa kufanya kazi na kazi zilizotolewa kama meza, tunasoma maadili ya pembejeo na pato kutoka kwenye viingilio vya meza na daima tunafanya kazi kutoka ndani hadi nje. Tunatathmini kazi ya ndani kwanza na kisha kutumia pato la kazi ya ndani kama pembejeo kwa kazi ya nje.

Mfano$\PageIndex{5}$: Using a Table to Evaluate a Composite Function

Kutumia Jedwali$\PageIndex{1}$, tathmini$f(g(3))$ na$g(f(3))$.

Jedwali$\PageIndex{1}$

$x$	$f(x)$	$g(x)$
\ (x\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">1	\ (f (x)\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">6	\ (g (x)\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">3
\ (x\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">2	\ (f (x)\)” style="wima align:katikati; msimamo wa maandishi:katikati;” class="lt-math-1296">8	\ (g (x)\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">5
\ (x\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">3	\ (f (x)\)” style="wima align:katikati; msimamo wa maandishi:katikati;” class="lt-math-1296">3	\ (g (x)\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">2
\ (x\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">4	\ (f (x)\)” style="wima align:katikati; msimamo wa maandishi:katikati;” class="lt-math-1296">1	\ (g (x)\)” style="wima align:katikati; msimamo wa maandishi:katikati;” class="lt-math-1296">7

Suluhisho

Ili kutathmini$f(g(3))$, tunaanza kutoka ndani na thamani ya pembejeo 3. Sisi kisha kutathmini kujieleza ndani$g(3)$ kwa kutumia meza inayofafanua kazi$g: g(3)=2$. Basi tunaweza kutumia kwamba matokeo kama pembejeo ya kazi$f$, hivyo$g(3)$ ni kubadilishwa na 2 na sisi kupata$f(2)$. Kisha, kwa kutumia meza kwamba amefafanua kazi$f$, tunaona kwamba$f(2)=8$.

$$g(3)=2 \nonumber$$

$$f(g(3))=f(2)=8 \nonumber$$

Ili kutathmini$g(f(3))$, sisi kwanza tathmini ya kujieleza ndani$f(3)$ kwa kutumia meza ya kwanza:$f(3)=3$. Kisha, kwa kutumia meza kwa$g$, tunaweza kutathmini

$$g(f(3))=g(3)=2 \nonumber$$

Jedwali$\PageIndex{2}$ linaonyesha kazi Composite$f{\circ}g$ na$g{\circ}f$ kama meza.

Jedwali$\PageIndex{2}$

$x$	$g(x)$	$f(g(x))$	$f(x)$	$g(f(x))$
\ (x\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">3	\ (g (x)\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">2	\ (f (g (x))\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">8	\ (f (x)\)” style="wima align:katikati; msimamo wa maandishi:katikati;” class="lt-math-1296">3	\ (g (f (x))\)” style="wima align:katikati; text-align:katikati;” class="lt-math-1296">2

Zoezi$\PageIndex{3}$

Kutumia Jedwali$\PageIndex{1}$, tathmini$f(g(1))$ na$g(f(4))$.

Jibu

$f(g(1))=f(3)=3$na$g(f(4))=g(1)=3$

Kutathmini Kazi za Composite Kutumia Grafu

Tunapopewa kazi za kibinafsi kama grafu, utaratibu wa kutathmini kazi za composite ni sawa na mchakato tunayotumia kwa kutathmini meza. Tunasoma maadili ya pembejeo na pato, lakini wakati huu, kutoka kwa x- na y-axes ya grafu.

Jinsi ya...

Kutokana na kazi ya composite na grafu ya kazi zake binafsi, tathmini kwa kutumia taarifa iliyotolewa na grafu.

1. Pata pembejeo iliyotolewa kwa kazi ya ndani kwenye x-axis ya grafu yake.
2. Soma pato la kazi ya ndani kutoka kwa y-axis ya grafu yake.
3. Pata pato la kazi ya ndani kwenye mhimili wa x wa grafu ya kazi ya nje.
4. Soma pato la kazi ya nje kutoka kwa mhimili wa y wa grafu yake. Hii ni pato la kazi ya composite.

Mfano$\PageIndex{6}$: Using a Graph to Evaluate a Composite Function

Kutumia Kielelezo$\PageIndex{3}$, tathmini$f(g(1))$.

Kielelezo$\PageIndex{3}$: Grafu mbili za parabola chanya na hasi.

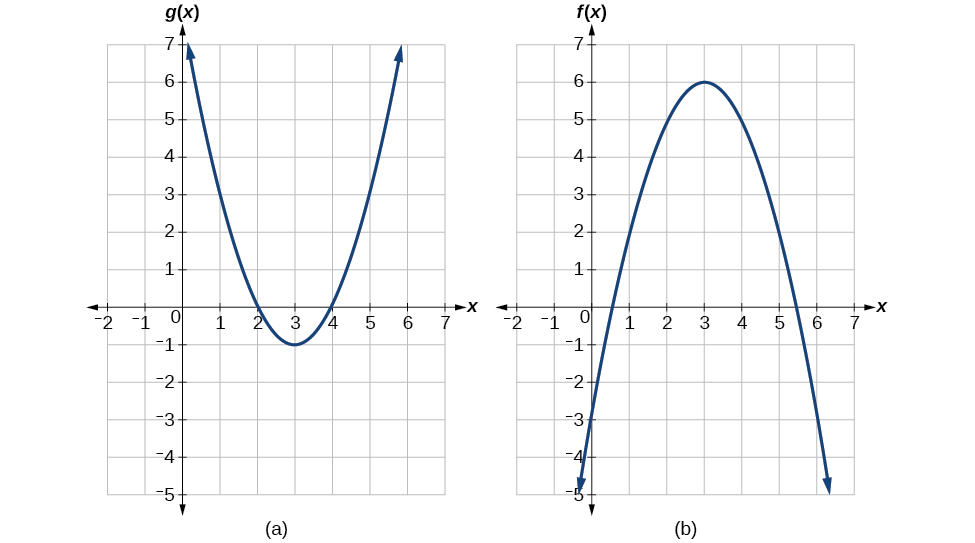
Suluhisho

Kutathmini$f(g(1))$, tunaanza na tathmini ya ndani. Angalia Kielelezo$\PageIndex{4}$.

Kielelezo$\PageIndex{4}$: Grafu mbili za parabola nzuri$g(x)$ na parabola hasi$f(x)$. Pointi zifuatazo zimepangwa:$g(1)=3$ na$f(3)=6$.

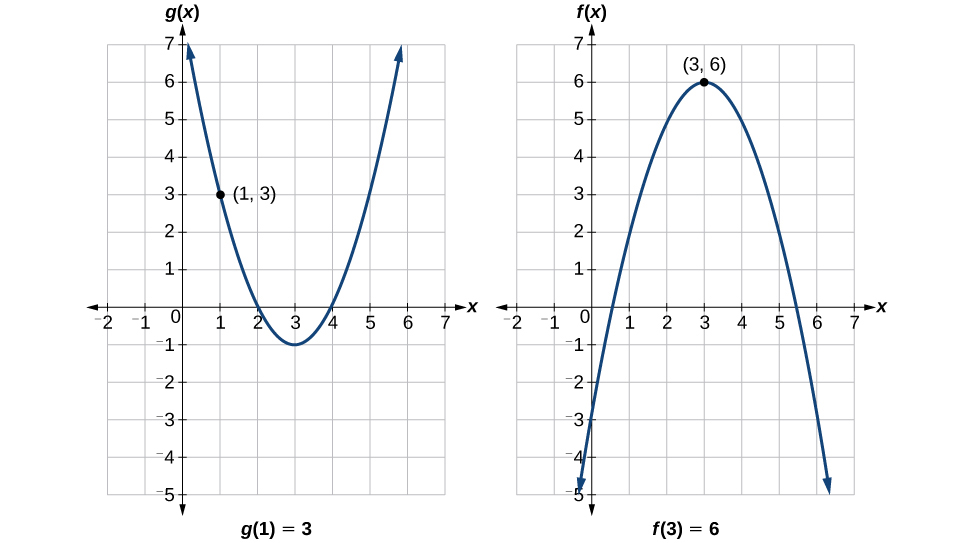
Sisi kutathmini$g(1)$ kutumia grafu ya$g(x)$, kutafuta pembejeo ya 1 kwenye x-axis na kutafuta thamani ya pato ya grafu katika pembejeo hiyo. Hapa,$g(1)=3$. Tunatumia thamani hii kama pembejeo kwa kazi$f$.

$$f(g(1))=f(3) \nonumber$$

Tunaweza kisha kutathmini kazi Composite kwa kuangalia grafu ya$f(x)$, kutafuta pembejeo ya 3 juu ya x-mhimili na kusoma thamani pato la grafu katika pembejeo hii. Hapa$f(3)=6$, hivyo,$f(g(1))=6$.

Uchambuzi

Kielelezo$\PageIndex{5}$ inaonyesha jinsi tunaweza alama grafu na mishale kufuatilia njia kutoka thamani ya pembejeo kwa thamani ya pato.

Kielelezo$\PageIndex{5}$: Grafu mbili za parabola chanya na hasi.

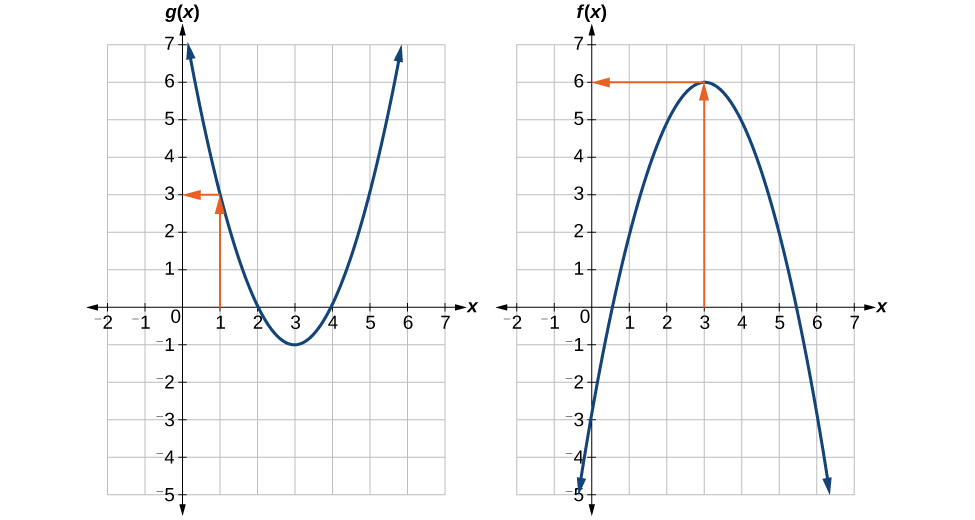
Zoezi$\PageIndex{4}$

Kutumia Kielelezo$\PageIndex{3}$, tathmini$g(f(2))$.

Jibu

$g(f(2))=g(5)=3$

Kutathmini Kazi za Composite Kutumia Fomu

Wakati wa kutathmini kazi ya composite ambapo tumeunda au tumepewa fomu, utawala wa kufanya kazi kutoka ndani nje unabaki sawa. Thamani ya pembejeo kwa kazi ya nje itakuwa pato la kazi ya ndani, ambayo inaweza kuwa thamani ya namba, jina la kutofautiana, au kujieleza ngumu zaidi.

Wakati tunaweza kutunga kazi kwa kila thamani ya pembejeo ya mtu binafsi, wakati mwingine ni muhimu kupata formula moja ambayo mahesabu ya matokeo ya muundo$f(g(x))$. Ili kufanya hivyo, tutaongeza wazo letu la tathmini ya kazi. Kumbuka kwamba, wakati sisi kutathmini kazi kama$f(t)=t^2−t$, sisi badala thamani ndani ya mabano katika formula popote tunaona variable pembejeo.

Jinsi ya...

Kutokana na fomu ya kazi ya composite, tathmini kazi.

1. Tathmini kazi ya ndani kwa kutumia thamani ya pembejeo au kutofautiana zinazotolewa.
2. Tumia pato linalosababisha kama pembejeo kwa kazi ya nje.

Mfano$\PageIndex{7}$: Evaluating a Composition of Functions Expressed as Formulas with a Numerical Input

Kutokana$f(t)=t^2−t$ na$h(x)=3x+2$, tathmini$f(h(1))$.

Suluhisho

Kwa sababu kujieleza ndani ni$h(1)$, tunaanza kwa kutathmini$h(x)$ saa 1.

$$\begin{align*} h(1)=3(1)+2 \\[4pt] h(1)&=5 \end{align*}$$

Kisha$f(h(1))=f(5)$, kwa hiyo tunatathmini$f(t)$ kwa pembejeo ya 5.

$$\begin{align*} f(h(1)) &=f(5) \\[5pt] f(h(1))&=5^2−5 \\[5pt] f(h(1))&=20 \end{align*}$$

Uchambuzi

Haina tofauti nini vigezo pembejeo$t$ na$x$ waliitwa katika tatizo hili kwa sababu sisi tathmini kwa maadili maalum namba.

Zoezi$\PageIndex{5}$

Kutokana$f(t)=t^2−t$ na$h(x)=3x+2$, kutathmini

a.$h(f(2))$
b.$h(f(−2))$

Jibu

8

Jibu b

20

Kutafuta Domain ya Kazi Composite

Kama tulivyojadiliwa hapo awali, uwanja wa kazi Composite kama$f{\circ}g$ vile unategemea uwanja wa$g$ na uwanja wa$f$. Ni muhimu kujua wakati tunaweza kutumia kazi ya composite na wakati hatuwezi, yaani, kujua uwanja wa kazi kama vile$f{\circ}g$. Hebu tufikiri tunajua nyanja za kazi$f$ na$g$ tofauti. Kama sisi kuandika kazi Composite kwa pembejeo$x$ kama$f(g(x))$, tunaweza kuona mara moja kwamba$x$ lazima kuwa mwanachama wa uwanja wa g ili kujieleza kuwa na maana, kwa sababu vinginevyo hatuwezi kukamilisha kazi ndani tathmini. Hata hivyo, sisi pia kuona kwamba$g(x)$ lazima kuwa mwanachama wa uwanja wa$f$, vinginevyo pili kazi tathmini katika$f(g(x))$ haiwezi kukamilika, na kujieleza bado haijulikani. Hivyo uwanja wa$f{\circ}g$ lina pembejeo wale tu katika uwanja wa$g$ kwamba kuzalisha matokeo kutoka$g$ mali ya uwanja wa$f$. Kumbuka kuwa uwanja wa$f$ linajumuisha$g$ ni seti ya yote$x$$x$ yaliyo katika uwanja wa$g$ na g (x)\) iko katika uwanja wa$f$.

Ufafanuzi: Domain ya Kazi Composite

Kikoa cha kazi ya composite$f(g(x))$ ni seti ya pembejeo hizo$x$ katika uwanja wa$g$ ambayo$g(x)$ iko katika uwanja wa$f$.

Jinsi ya...

Kutokana na utungaji wa kazi$f(g(x))$, tambua kikoa chake.

1. Kupata uwanja wa$g$.
2. Kupata uwanja wa$f$.
3. Pata pembejeo hizo$x$ katika uwanja wa$g$ ambayo$g(x)$ iko katika uwanja wa$f$. Hiyo ni, ukiondoa pembejeo hizo$x$ kutoka kwenye uwanja wa$g$ ambayo$g(x)$ sio katika uwanja wa$f$. Seti inayosababisha ni uwanja wa$f{\circ}g$.

Mfano$\PageIndex{8A}$: Finding the Domain of a Composite Function

Pata uwanja wa

$$(f∘g)(x) \text{ where } f(x)=\dfrac{5}{x−1} \text{ and } g(x)=\dfrac{4}{3x−2} \nonumber$$

Suluhisho

Uwanja wa$g(x)$ lina namba zote halisi isipokuwa$x=\frac{2}{3}$, tangu thamani ya pembejeo hiyo ingeweza kutufanya tugawanye na 0. Vivyo hivyo, uwanja wa$f$ lina namba zote halisi isipokuwa 1. Kwa hiyo tunahitaji kuwatenga kutoka kwenye uwanja wa$g(x)$$x$ thamani hiyo ambayo$g(x)=1$.

$$\begin{align*} \dfrac{4}{3x-2}&= 1 \\[4pt] 4 &=3x-2 \\[4pt] 6&=3x \\[4pt] x&= 2 \end{align*}$$

Hivyo uwanja wa$f{\circ}g$ ni seti ya namba zote halisi isipokuwa$\frac{2}{3}$ na$2$. Hii ina maana kwamba

$$x{\neq} \dfrac{2}{3} \text{ or } x\neq2 \nonumber$$

Tunaweza kuandika hii katika nukuu ya muda kama

$$\left(−\infty,\dfrac{2}{3}\right)\cup \left(\dfrac{2}{3},2 \right)\cup \left(2,\infty \right) \nonumber$$

Mfano$\PageIndex{8B}$: Finding the Domain of a Composite Function Involving Radicals

Pata uwanja wa

$$(f{\circ}g)(x) \text{ where } f(x)=\sqrt{x+2} \text{ and } g(x)=\sqrt{3−x} \nonumber$$

Suluhisho

Kwa sababu hatuwezi kuchukua mizizi ya mraba ya namba hasi, uwanja wa$g$ ni$\left(−\infty,3\right]$. Sasa tunaangalia uwanja wa kazi ya composite

$$(f{\circ}g)(x)=\sqrt{\sqrt{3−x}+2} \nonumber$$

Kwa$(f∘g)(x)=\sqrt{ \sqrt{3−x}+2},\sqrt{3−x}+2≥0,$ kuwa radicand ya mizizi ya mraba lazima iwe chanya. Kwa kuwa mizizi ya mraba ni chanya$\sqrt{3−x}≥0$,, au,$3−x≥0,$ ambayo inatoa uwanja wa$(-∞,3]$.

Uchambuzi

Mfano huu unaonyesha kwamba ujuzi wa kazi mbalimbali (hasa kazi ya ndani) pia inaweza kusaidia katika kutafuta uwanja wa kazi ya composite. Pia inaonyesha kwamba uwanja wa$f{\circ}g$ inaweza kuwa na maadili ambayo si katika uwanja wa$f$, ingawa ni lazima kuwa katika uwanja wa$g$.

Zoezi$\PageIndex{6}$

Pata uwanja wa

$$(f{\circ}g)(x) \text{ where } f(x)=\dfrac{1}{x−2} \text{ and } g(x)=\sqrt{x+4} \nonumber$$

Jibu

$[−4,0)∪(0,∞)$

Kuharibu Kazi ya Composite katika Kazi zake za Kipengele

Katika hali nyingine, ni muhimu kuharibu kazi ngumu. Kwa maneno mengine, tunaweza kuandika kama muundo wa kazi mbili rahisi. Kunaweza kuwa na njia zaidi ya moja ya kuharibu kazi ya composite, hivyo tunaweza kuchagua utengano unaoonekana kuwa unafaa zaidi.

Mfano$\PageIndex{9}$: Decomposing a Function

Andika$f(x)=\sqrt{5−x^2}$ kama muundo wa kazi mbili.

Suluhisho

Tunatafuta kazi mbili,$g$ na$h$, hivyo$f(x)=g(h(x))$. Ili kufanya hivyo, tunatafuta kazi ndani ya kazi katika formula kwa$f(x)$. Kama uwezekano mmoja, tunaweza taarifa kwamba kujieleza$5−x^2$ ni ndani ya mizizi mraba. Tunaweza kisha kuoza kazi kama

$$h(x)=5−x^2 \text{ and } g(x)=\sqrt{x} \nonumber$$

Tunaweza kuangalia jibu letu kwa kurejesha kazi.

$$g(h(x))=g(5−x^2)=\sqrt{5−x^2} \nonumber$$

Zoezi$\PageIndex{7}$

Andika$f(x)=\dfrac{4}{3−\sqrt{4+x^2}}$ kama muundo wa kazi mbili.

Jibu

Majibu iwezekanavyo:

$g(x)=\sqrt{4+x^2}$

$h(x)=\dfrac{4}{3−x}$

$f=h{\circ}g$

Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na kazi Composite.

• Kazi Composite (http://openstaxcollege.org/l/compfunction)
• Composite Kazi Nukuu Maombi (http://openstaxcollege.org/l/compfuncnot)
• Kazi Composite Kutumia Grafu (http://openstaxcollege.org/l/compfuncgraph)
• Kuoza Kazi (http://openstaxcollege.org/l/decompfunction)
• Maadili ya Kazi ya Composite (http://openstaxcollege.org/l/compfuncvalue)

Mlinganyo muhimu

• Kazi ya Composite$(f{\circ}g)(x)=f(g(x))$

Dhana muhimu

• Tunaweza kufanya shughuli za algebraic kwenye kazi. Angalia Mfano.
• Wakati kazi zimeunganishwa, pato la kazi ya kwanza (ndani) inakuwa pembejeo ya kazi ya pili (nje).
• Kazi iliyozalishwa kwa kuchanganya kazi mbili ni kazi ya composite. Angalia Mfano na Mfano.
• Utaratibu wa utungaji wa kazi lazima uzingatiwe wakati wa kutafsiri maana ya kazi za composite. Angalia Mfano.
• Kazi ya composite inaweza kupimwa kwa kutathmini kazi ya ndani kwa kutumia thamani ya pembejeo iliyotolewa na kisha kutathmini kazi ya nje kuchukua kama pembejeo yake pato la kazi ya ndani.
• Kazi ya composite inaweza kupimwa kutoka meza. Angalia Mfano.
• Kazi ya composite inaweza kupimwa kutoka kwenye grafu. Angalia Mfano.
• Kazi ya composite inaweza kupimwa kutoka kwa formula. Angalia Mfano.
• Kikoa cha kazi ya composite lina pembejeo hizo katika uwanja wa kazi ya ndani ambayo yanahusiana na matokeo ya kazi ya ndani ambayo iko katika uwanja wa kazi ya nje. Angalia Mfano na Mfano.
• Kama vile kazi zinaweza kuunganishwa ili kuunda kazi ya composite, kazi za composite zinaweza kuharibiwa katika kazi rahisi.
• Kazi zinaweza kuharibiwa kwa njia zaidi ya moja. Angalia Mfano.

faharasa

kazi ya composite

kazi mpya iliyoundwa na utungaji wa kazi, wakati pato la kazi moja linatumiwa kama pembejeo ya mwingine