1.3: Viwango vya Mabadiliko na Tabia ya Grafu
- Page ID
- 181180
Malengo ya kujifunza
- Kupata kiwango cha wastani wa mabadiliko ya kazi.
- Tumia grafu ili kuamua ambapo kazi inaongezeka, kupungua, au mara kwa mara.
- Tumia grafu ili kupata maxima ya ndani na minima ya ndani.
- Tumia grafu ili upate kiwango cha juu kabisa na cha chini kabisa.
Gharama za petroli zimepata kushuka kwa thamani ya mwitu zaidi ya miongo kadhaa iliyopita. Jedwali\(\PageIndex{1}\) linataja wastani wa gharama, kwa dola, ya lita moja ya petroli kwa miaka 2005—2012. Gharama ya petroli inaweza kuchukuliwa kama kazi ya mwaka.
| \(y\) | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|---|---|---|
| \(C(y)\) | 2.31 | 2.62 | 2.84 | 3.30 | 2.41 | 2.84 | 3.58 | 3.68 |
Kama tulikuwa na nia tu jinsi bei ya petroli iliyopita kati ya 2005 na 2012, tunaweza kukokotoa kwamba gharama kwa kila lita ilikuwa imeongezeka kutoka $2.31 hadi $3.68, ongezeko la $1.37. Ingawa hii ni ya kuvutia, inaweza kuwa muhimu zaidi kuangalia ni kiasi gani bei iliyopita kwa mwaka. Katika sehemu hii, tutachunguza mabadiliko kama haya.
Kutafuta Kiwango cha Wastani cha Mabadiliko ya Kazi
Mabadiliko ya bei kwa mwaka ni kiwango cha mabadiliko kwa sababu inaelezea jinsi kiasi cha pato kinabadilika kuhusiana na mabadiliko katika wingi wa pembejeo. Tunaweza kuona kwamba bei ya petroli katika Jedwali\(\PageIndex{1}\) haikubadilika kwa kiasi sawa kila mwaka, hivyo kiwango cha mabadiliko haikuwa mara kwa mara. Ikiwa tunatumia data ya mwanzo na mwisho tu, tungepata kiwango cha wastani cha mabadiliko katika kipindi maalum cha muda. Ili kupata kiwango cha wastani cha mabadiliko, tunagawanya mabadiliko katika thamani ya pato kwa mabadiliko katika thamani ya pembejeo.
\[\begin{align*} \text{Average rate of change}&=\dfrac{\text{Change in output}}{\text{Change in input}} \\[4pt] &=\dfrac{\Delta y}{\Delta x}\\[4pt] &=\dfrac{y_2-y_1}{x_2-x_1}\\[4pt] &=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\end{align*} \label{1.3.1}\]
Barua ya Kigiriki\(\Delta\) (delta) inaashiria mabadiliko kwa wingi; tunasoma uwiano kama “delta-\(y\) over delta-\(x\)” au “mabadiliko katika\(y\) kugawanywa na mabadiliko katika\(x\).” Mara kwa mara sisi kuandika\(\Delta f\) badala ya\(\Delta y\), ambayo bado inawakilisha mabadiliko katika thamani ya kazi ya pato kutokana na mabadiliko ya thamani yake pembejeo. Haimaanishi sisi ni kubadilisha kazi katika baadhi ya kazi nyingine.
Katika mfano wetu, bei ya petroli iliongezeka kwa $1.37 kutoka 2005 hadi 2012. Zaidi ya miaka 7, kiwango cha wastani wa mabadiliko
\[\dfrac{\Delta y}{\Delta x}=\dfrac{$1.37}{7 \text{years}}\approx \text{0.196 dollars per year.} \label{1.3.2}\]
Kwa wastani, bei ya gesi iliongezeka kwa karibu 19.6€ kila mwaka. Mifano mingine ya viwango vya mabadiliko ni pamoja na:
- Idadi ya panya kuongezeka kwa panya 40 kwa wiki
- gari kusafiri 68 maili kwa saa (umbali alisafiri mabadiliko na 68 maili kila saa kama wakati unapita)
- gari kuendesha gari 27 maili kwa kila lita (umbali alisafiri mabadiliko kwa 27 maili kwa kila lita)
- Ya sasa kupitia mzunguko wa umeme unaongezeka kwa 0.125 amperes kwa kila volt ya voltage iliyoongezeka
- Kiasi cha fedha katika akaunti ya chuo kupungua kwa $4,000 kwa robo
Ufafanuzi: Kiwango cha Mabadiliko
Kiwango cha mabadiliko kinaelezea jinsi kiasi cha pato kinabadilika kuhusiana na mabadiliko katika kiasi cha pembejeo. Vitengo vya kiwango cha mabadiliko ni “vitengo vya pato kwa vitengo vya pembejeo.”
Kiwango cha wastani cha mabadiliko kati ya maadili mawili ya pembejeo ni mabadiliko ya jumla ya maadili ya kazi (maadili ya pato) imegawanywa na mabadiliko katika maadili ya pembejeo.
\[\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\]
Jinsi ya...
Kutokana na thamani ya kazi kwa pointi tofauti, hesabu kiwango cha wastani cha mabadiliko ya kazi kwa muda kati ya maadili mawili\(x_1\) na\(x_2\).
- Tumia tofauti\(y_2−y_1=\Delta y\).
- Tumia tofauti\(x_2−x_1=\Delta x\).
- Pata uwiano\(\dfrac{\Delta y}{\Delta x}\).
Mfano\(\PageIndex{1}\): Computing an Average Rate of Change
Kutumia data katika Jedwali\(\PageIndex{1}\), pata kiwango cha wastani cha mabadiliko ya bei ya petroli kati ya 2007 na 2009.
Suluhisho
Mwaka 2007, bei ya petroli ilikuwa $2.84. Mwaka 2009, gharama ilikuwa $2.41. Kiwango cha wastani wa mabadiliko ni
\[\begin{align*} \dfrac{\Delta y}{\Delta x}&=\dfrac{y_2−y_1}{x_2−x_1} \\[4pt] &=\dfrac{$2.41−$2.84}{2009−2007} \\[4pt] &=\dfrac{−$0.43}{2 \text{ years}} \\[4pt] &=−$0.22 \text{ per year} \end{align*}\]
Uchambuzi
Kumbuka kuwa kupungua kunaonyeshwa na mabadiliko mabaya au “ongezeko hasi.” Kiwango cha mabadiliko ni hasi pale pato linapungua kadiri pembejeo inapoongezeka au pato linapoongezeka kadiri pembejeo inapungua.
Zoezi\(\PageIndex{1}\)
Kutumia data katika Jedwali\(\PageIndex{1}\), pata kiwango cha wastani cha mabadiliko kati ya 2005 na 2010.
- Suluhisho
-
\(\dfrac{$2.84−$2.315}{5 \text{ years}} =\dfrac{$0.535}{5 \text{ years}} =$0.106 \text{per year.}\)
Mfano\(\PageIndex{2}\): Computing Average Rate of Change from a Graph
Kutokana na kazi\(g(t)\) iliyoonyeshwa kwenye Kielelezo\(\PageIndex{1}\), pata kiwango cha wastani cha mabadiliko wakati\([−1,2]\).
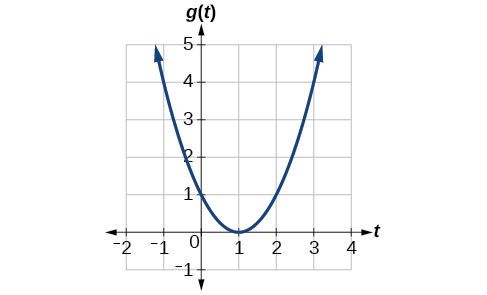
Suluhisho
Katika\(t=−1\), Kielelezo\(\PageIndex{2}\) kinaonyesha\(g(−1)=4\). Katika\(t=2\), grafu inaonyesha\(g(2)=1\).
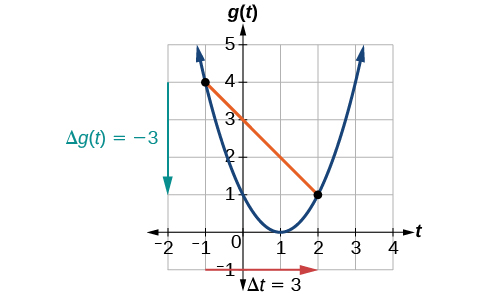
Mabadiliko ya usawa\(\Delta t=3\) yanaonyeshwa na mshale mwekundu-nyekundu, na mabadiliko ya wima\(\Delta g(t)=−3\) yanaonyeshwa na mshale wa turquoise. mabadiliko ya pato kwa -3 wakati pembejeo mabadiliko kwa 3, kutoa kiwango cha wastani wa mabadiliko ya
\[\dfrac{1−4}{2−(−1)}=\dfrac{−3}{3}=−1\]
Uchambuzi
Kumbuka kwamba utaratibu tunaochagua ni muhimu sana. Ikiwa, kwa mfano, tunatumia\(\dfrac{y_2−y_1}{x_1−x_2}\), hatuwezi kupata jibu sahihi. Chagua hatua ambayo itakuwa 1 na ambayo hatua itakuwa 2, na kuweka kuratibu fasta kama\((x_1,y_1)\) na\((x_2,y_2)\).
Mfano\(\PageIndex{3}\): Computing Average Rate of Change from a Table
Baada ya kumchukua rafiki ambaye anaishi umbali wa maili 10, Anna anarekodi umbali wake kutoka nyumbani kwa muda. Maadili yanaonyeshwa katika Jedwali\(\PageIndex{2}\). Kupata kasi yake ya wastani juu ya kwanza 6 masaa.
| \(t\)(masaa) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| \(D(t)\)(maili) | 10 | 55 | 90 | 153 | 214 | 240 | 292 | 300 |
Suluhisho
Hapa, kasi ya wastani ni kiwango cha wastani cha mabadiliko. Alisafiri 292 maili katika masaa 6, kwa kasi ya wastani wa
\[\begin{align*}\dfrac{292−10}{6−0}&=\dfrac{282}{6}\\[4pt] &= 47\end{align*}\]
Kasi ya wastani ni karibu maili 47 kwa saa.
Uchambuzi
Kwa sababu kasi sio mara kwa mara, kasi ya wastani inategemea muda uliochaguliwa. Kwa muda\([2,3]\), kasi ya wastani ni maili 63 kwa saa.
Mfano\(\PageIndex{4}\): Computing Average Rate of Change for a Function Expressed as a Formula
Compute kiwango cha wastani wa mabadiliko ya\(f(x)=x^2−\frac{1}{x}\) juu ya muda\([2, 4]\).
Suluhisho
Tunaweza kuanza kwa kompyuta maadili ya kazi katika kila mwisho wa muda.
\[\begin{align*}f(2)&=2^2−\frac{1}{2} f(4)&=4^2−\frac{1}{4} \\[4pt] &=4−\frac{1}{2} &=16−\frac{1}{4} \\[4pt] &=72 &=\frac{63}{4}\end{align*}\]
Sasa tunakokotoa kiwango cha wastani cha mabadiliko.
\[\begin{align*}\text{Average rate of change} &=\dfrac{f(4)−f(2)}{4−2} \\[4pt] &=\dfrac{\frac{63}{4}-\frac{7}{2}}{4-2} \\[4pt] &=\dfrac{\frac{49}{4}}{2} \\[4pt] &= \dfrac{49}{8}\end{align*}\]
Zoezi\(\PageIndex{2}\)
Kupata kiwango cha wastani wa mabadiliko ya\(f(x)=x−2\sqrt{x}\) juu ya muda\([1, 9]\).
- Suluhisho
-
\(\frac{1}{2}\)
Mfano\(\PageIndex{5}\): Finding the Average Rate of Change of a Force
Nguvu ya umeme\(F\), iliyopimwa kwa newtons, kati ya chembe mbili za kushtakiwa inaweza kuhusiana na umbali kati ya chembe\(d\), kwa sentimita, kwa formula\(F(d)=\frac{2}{d^2}\). Pata kiwango cha wastani cha mabadiliko ya nguvu ikiwa umbali kati ya chembe huongezeka kutoka cm 2 hadi 6 cm.
Suluhisho
Sisi ni kompyuta kiwango cha wastani wa mabadiliko ya\(F(d)=\dfrac{2}{d^2}\) juu ya muda\([2,6]\).
\[\begin{align*}\text{Average rate of change }&=\dfrac{F(6)−F(2)}{6−2} \\[4pt] &=\dfrac{\frac{2}{6^2}-\frac{2}{2^2}}{6-2} & \text{Simplify} \\[4pt] &=\dfrac{\frac{2}{36}-\frac{2}{4}}{4} \\[4pt] &=\dfrac{-\frac{16}{36}}{4} & \text{Combine numerator terms.} \\[4pt] &=−\dfrac{1}{9} & \text{Simplify}\end{align*}\]
Kiwango cha wastani cha mabadiliko ni\(−\frac{1}{9}\) newton kwa sentimita.
Mfano\(\PageIndex{6}\): Finding an Average Rate of Change as an Expression
Kupata kiwango cha wastani wa mabadiliko ya\(g(t)=t^2+3t+1\) juu ya muda\([0, a]\). Jibu litakuwa kujieleza kuwashirikisha\(a\).
Suluhisho
Tunatumia kiwango cha wastani cha formula ya mabadiliko.
\(\begin{align*}\text{Average rate of change} &=\dfrac{g(a)−g(0)}{a−0} & \text{Evaluate.} \\[4pt] &=\dfrac{(a^2+3a+1)−(0^2+3(0)+1)}{a−0} & \text{Simplify.} \\[4pt] &=\dfrac{a^2+3a+1−1}{a} & \text{Simplify and factor.}\\[4pt] &= \dfrac{a(a+3)}{a} & \text{Divide by the common factor a.}\\[4pt] &= a+3 \end{align*}\)
Matokeo haya inatuambia kiwango cha wastani cha mabadiliko katika suala la kati\(t=0\) na hatua nyingine yoyote\(t=a\). Kwa mfano, kwa muda\([0,5]\), kiwango cha wastani cha mabadiliko kitakuwa\(5+3=8\).Zoezi\(\PageIndex{3}\)
Kupata kiwango cha wastani wa mabadiliko ya\(f(x)=x^2+2x−8\) juu ya muda\([5, a]\).
- Suluhisho
-
\(a+7\)
Kutumia Grafu ili Kuamua Ambapo Kazi inaongezeka, Kupungua, au Mara kwa mara
Kama sehemu ya kuchunguza jinsi kazi zinavyobadilika, tunaweza kutambua vipindi ambavyo kazi inabadilika kwa njia maalum. Tunasema kuwa kazi inaongezeka kwa muda ikiwa maadili ya kazi yanaongezeka kama maadili ya pembejeo yanaongezeka ndani ya kipindi hicho. Vile vile, kazi inapungua kwa muda ikiwa maadili ya kazi yanapungua kama maadili ya pembejeo yanaongezeka zaidi ya muda huo. Kiwango cha wastani cha mabadiliko ya kazi inayoongezeka ni chanya, na kiwango cha wastani cha mabadiliko ya kazi ya kupungua ni hasi. Kielelezo\(\PageIndex{3}\) inaonyesha mifano ya kuongeza na kupunguza vipindi juu ya kazi.
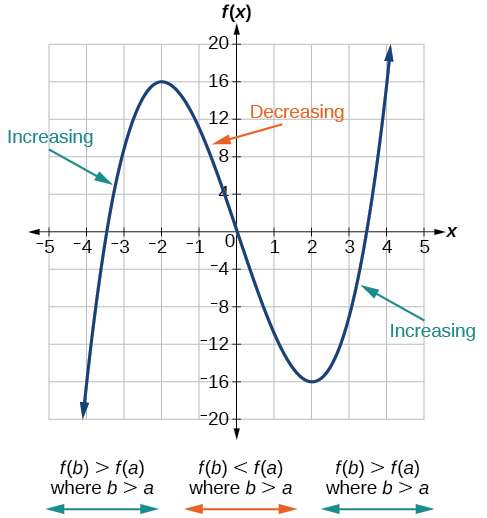
Wakati baadhi ya kazi zinaongezeka (au kupungua) juu ya uwanja wao wote, wengine wengi hawana. Thamani ya pembejeo ambapo kazi inabadilika kuongezeka hadi kupungua (tunapoenda kutoka kushoto kwenda kulia, yaani, kama ongezeko la kutofautiana kwa pembejeo) linaitwa upeo wa ndani. Kama kazi ina zaidi ya moja, tunasema ina maxima ndani. Vile vile, thamani ya pembejeo ambapo kazi inabadilika kutoka kupungua hadi kuongezeka kama ongezeko la kutofautiana kwa pembejeo inaitwa kiwango cha chini cha ndani. Fomu ya wingi ni “minima ya ndani.” Pamoja, maxima ya ndani na minima huitwa extrema ya ndani, au maadili ya ndani, ya kazi. (Fomu ya umoja ni “uliokithiri.”) Mara nyingi, neno la ndani linabadilishwa na jamaa ya muda. Katika maandishi haya, tutatumia neno ndani.
Kwa wazi, kazi haina kuongezeka wala kupungua kwa muda ambapo ni mara kwa mara. Kazi pia haina kuongezeka wala kupungua kwa extrema. Kumbuka kwamba tunapaswa kuzungumza juu ya extrema ya ndani, kwa sababu yoyote ya mwisho ya ndani kama ilivyoelezwa hapa sio lazima kiwango cha juu au cha chini kabisa katika uwanja wote wa kazi.
Kwa kazi ambayo grafu inavyoonekana kwenye Kielelezo\(\PageIndex{4}\), upeo wa ndani ni 16, na hutokea\(x=−2\). Kima cha chini cha mitaa ni -16 na kinatokea saa\(x=2\).
![Grafu ya polynomial inayoonyesha vipindi vya kuongezeka na kupungua na upeo wa ndani.] Ufafanuzi wa upeo wa ndani](https://math.libretexts.org/@api/deki/files/916/CNX_Precalc_Figure_01_03_014.jpg)
Ili kupata maxima ya ndani na minima kutoka kwenye grafu, tunahitaji kuchunguza grafu ili tuone wapi grafu inapata pointi zake za juu na za chini kabisa, kwa mtiririko huo, ndani ya muda wa wazi. Kama mkutano wa coaster roller, grafu ya kazi ni ya juu katika upeo wa ndani kuliko katika maeneo ya karibu pande zote mbili. Grafu pia itakuwa chini kwa kiwango cha chini cha ndani kuliko kwenye maeneo ya jirani. Kielelezo\(\PageIndex{5}\) unaeleza mawazo haya kwa upeo wa ndani.
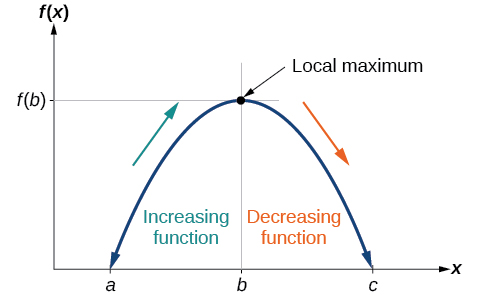
Uchunguzi huu unatuongoza kwa ufafanuzi rasmi wa extrema za mitaa.
Minima ya Mitaa na Maxima ya Mitaa
- Kazi\(f\) ni kazi inayoongezeka kwa muda wa wazi ikiwa\(f(b)>f(a)\) kwa kila\(a\),\(b\) muda ambapo\(b>a\).
- Kazi\(f\) ni kazi ya kupungua kwa muda wa wazi ikiwa\(f(b)<f(a)\) kwa kila\(a\),\(b\) muda ambapo\(b>a\).
Kazi\(f\) ina upeo wa ndani kwa hatua\(b\) katika kipindi cha wazi\((a,c)\) ikiwa\(f(b)\) ni kubwa kuliko au sawa na\(f(x)\) kwa kila hatua\(x\) (\(x\)haifai\(b\)) katika kipindi. Vivyo hivyo,\(f\) ina kiwango cha chini ndani\(b\) katika hatua katika\((a,c)\) kama\(f(b)\) ni chini ya au sawa na\(f(x)\) kwa kila\(x\) (\(x\)hana sawa\(b\)) katika kipindi.
Mfano\(\PageIndex{7}\) Finding Increasing and Decreasing Intervals on a Graph
Kutokana na kazi\(p(t)\) katika Kielelezo\(\PageIndex{6}\), tambua vipindi ambavyo kazi inaonekana kuongezeka.
![[Grafu ya polynomial.]](https://math.libretexts.org/@api/deki/files/920/CNX_Precalc_Figure_01_03_006.jpg)
Suluhisho
Tunaona kwamba kazi si mara kwa mara juu ya muda wowote. Kazi ni kuongeza ambapo slants juu kama sisi hoja ya haki na kupungua ambapo slants chini kama sisi hoja ya haki. Kazi inaonekana kuongezeka kutoka\(t=1\) kwenda\(t=3\) na kutoka\(t=4\) juu.
Katika notation ya muda, tunaweza kusema kazi inaonekana kuongezeka kwa muda\((1,3)\) na muda\((4,\infty)\).
Uchambuzi
Kumbuka katika mfano huu kwamba sisi kutumika vipindi wazi (vipindi kwamba si ni pamoja na endpoints), kwa sababu kazi ni wala kuongeza wala kupungua katika\(t=1\),\(t=3\), na\(t=4\). Vipengele hivi ni extrema ya ndani (minima mbili na kiwango cha juu).
Mfano\(\PageIndex{8}\): Finding Local Extrema from a Graph
Graph kazi\(f(x)=\frac{2}{x}+\frac{x}{3}\). Kisha tumia grafu ili kukadiria extrema ya ndani ya kazi na kuamua vipindi ambavyo kazi inaongezeka.
Suluhisho
Kutumia teknolojia, tunaona kwamba grafu ya kazi inaonekana kama hiyo katika Kielelezo\(\PageIndex{7}\). Inaonekana kuna hatua ya chini, au kiwango cha chini cha ndani, kati\(x=2\) na\(x=3\), na kiwango cha juu cha kioo-picha, au upeo wa ndani, mahali fulani kati\(x=−3\) na\(x=−2\)
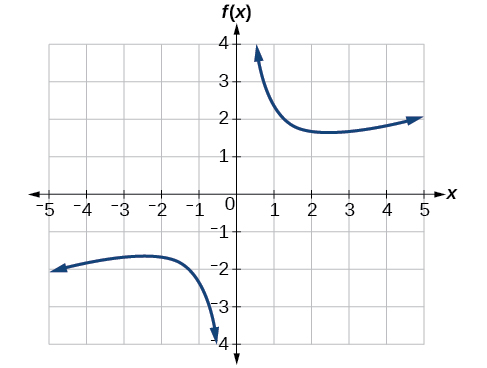 .
.
Uchambuzi
Wengi wa mahesabu ya graphing na huduma za graphing wanaweza kukadiria eneo la maxima na minima. Kielelezo\(\PageIndex{8}\) hutoa picha za skrini kutoka teknolojia mbili tofauti, kuonyesha makadirio ya kiwango cha juu na cha chini.
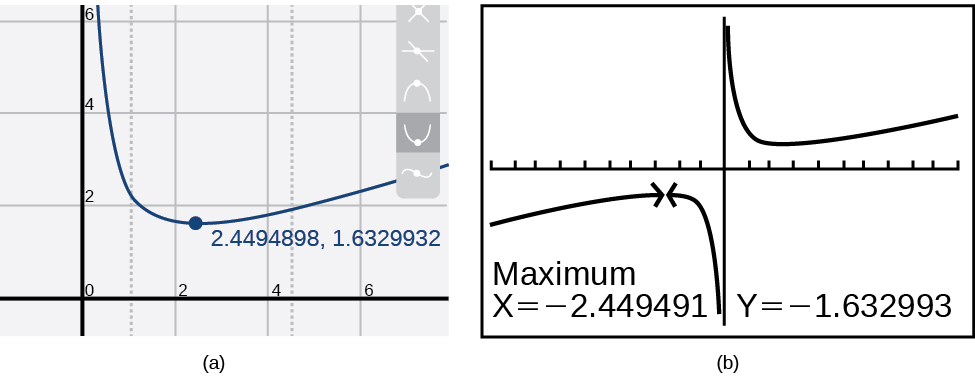
Kulingana na makadirio haya, kazi inaongezeka kwa muda\((−\infty,−2.449)\) na\((2.449,\infty)\). Kumbuka kwamba, wakati tunatarajia extrema kuwa symmetric, teknolojia mbili tofauti kukubaliana tu hadi decimals nne kutokana na tofauti algorithms makadirio kutumiwa na kila. (Eneo halisi la extrema ni saa\(\pm\sqrt{6}\), lakini kuamua hii inahitaji calculus.)
Zoezi\(\PageIndex{8}\)
Grafu kazi\(f(x)=x^3−6x^2−15x+20\) ili kukadiria extrema ya ndani ya kazi. Tumia hizi kuamua vipindi ambavyo kazi inaongezeka na kupungua.
- Suluhisho
-
Upeo wa ndani unaonekana kutokea\((−1,28)\), na kiwango cha chini cha ndani kinatokea\((5,−80)\). Kazi inaongezeka\((−\infty,−1)\cup(5,\infty)\) na kupungua\((−1,5)\).
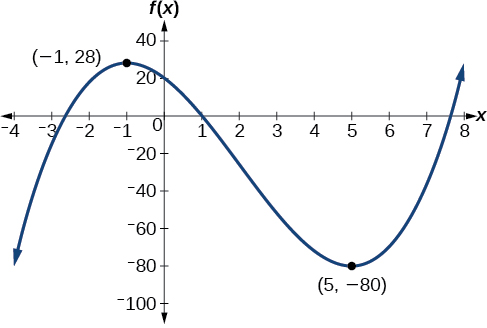
Grafu ya polynomial yenye upeo wa ndani (-1, 28) na kiwango cha chini cha ndani (5, -80).
Mfano\(\PageIndex{9}\): Finding Local Maxima and Minima from a Graph
Kwa kazi ya grafu ambayo inavyoonyeshwa kwenye Kielelezo\(\PageIndex{9}\), pata kiwango cha juu na cha chini cha ndani.
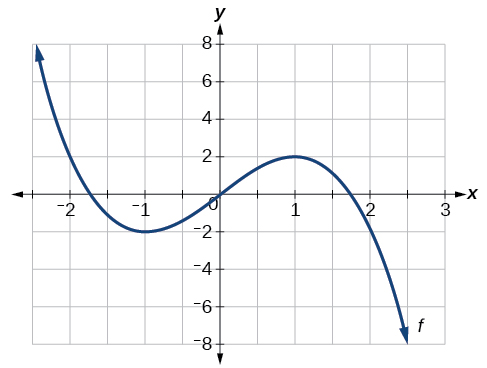
Suluhisho
Angalia grafu ya\(f\). Grafu inafikia upeo wa ndani\(x=1\) kwa sababu ni hatua ya juu katika kipindi cha wazi\(x=1\) karibu.Upeo wa ndani ni y-kuratibu saa\(x=1\), ambayo ni 2.
Grafu inafikia kiwango cha chini cha ndani\(x=−1\) kwa sababu ni hatua ya chini kabisa katika kipindi cha wazi kote\(x=−1\). Kiwango cha chini cha mitaa ni y-kuratibu saa\(x=−1\), ambayo ni -1.
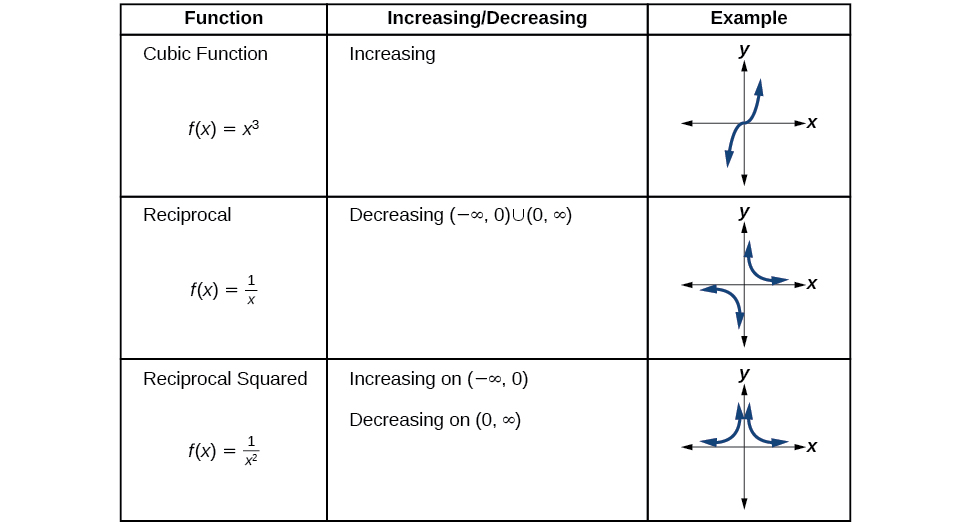
Kuchambua Kazi za Toolkit kwa Vipindi vya Kuongezeka au Kupungua
Sisi sasa kurudi kazi zetu toolkit na kujadili tabia zao graphical katika Kielelezo\(\PageIndex{10}\), Kielelezo\(\PageIndex{11}\), na Kielelezo\(\PageIndex{12}\).

 .
.
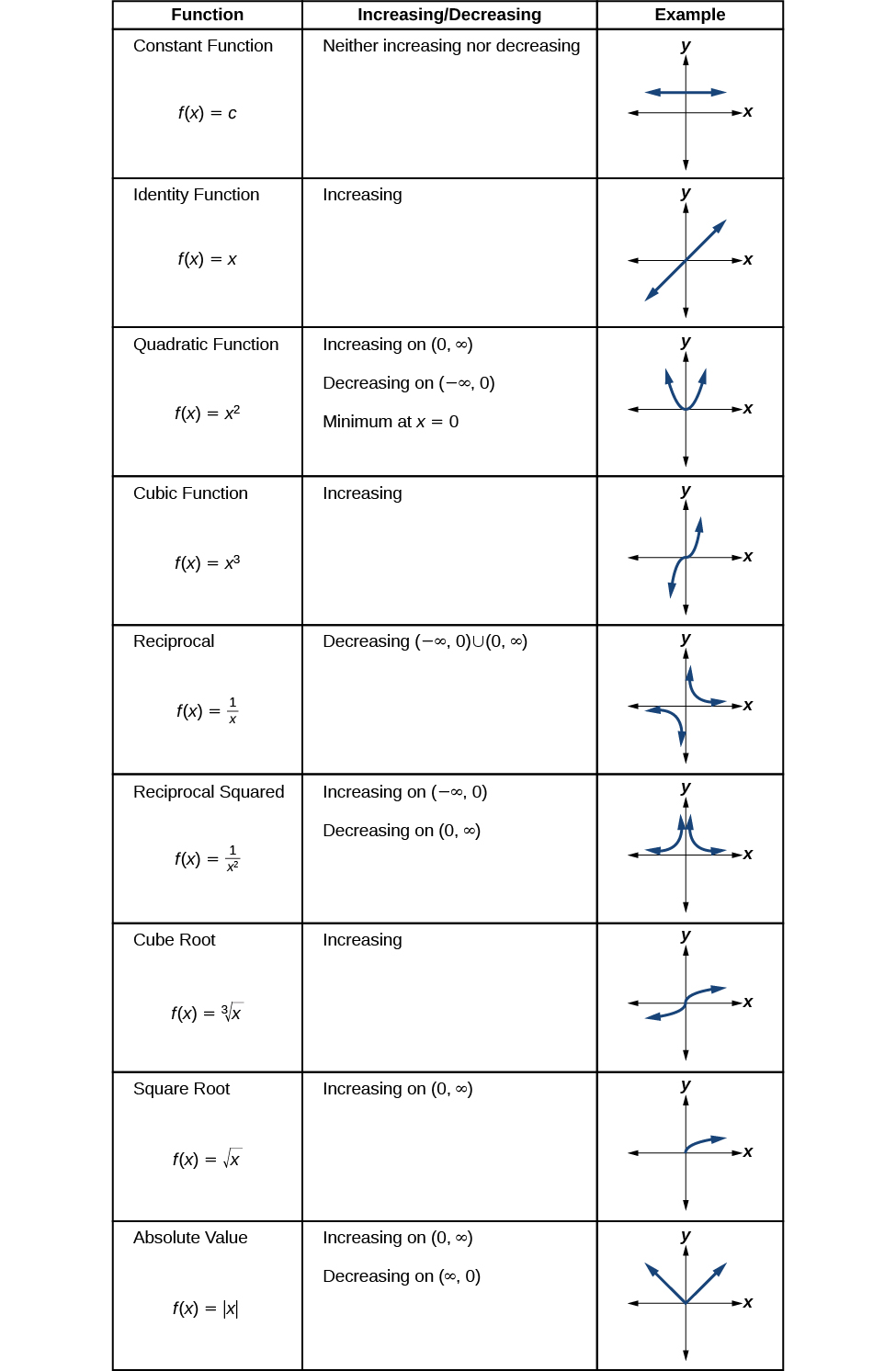
Kielelezo\(\PageIndex{12}\)
Tumia Grafu ili Machapisho Kiwango cha juu kabisa na Kiwango cha chini kabisa
Kuna tofauti kati ya kupata pointi za juu na za chini zaidi kwenye grafu katika kanda karibu na muda wa wazi (ndani ya nchi) na kupata pointi za juu na za chini zaidi kwenye grafu kwa uwanja mzima. Kuratibu y-( pato) kwenye pointi za juu na za chini huitwa kiwango cha juu kabisa na cha chini kabisa, kwa mtiririko huo. Ili kupata maxima kabisa na minima kutoka kwenye grafu, tunahitaji kuchunguza grafu ili tuone wapi grafu inapata pointi za juu na za chini kabisa kwenye uwanja wa kazi (Kielelezo\(\PageIndex{13}\)).
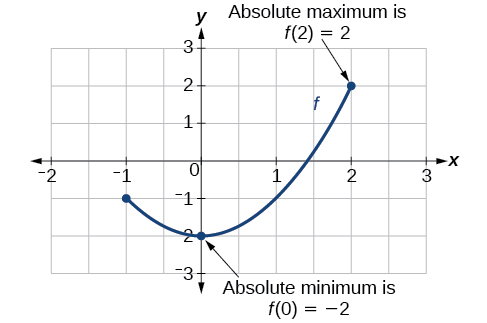
Si kila kazi ina kiwango cha juu kabisa au thamani ya chini. Kazi ya toolkit\(f(x)=x^3\) ni moja ya kazi hiyo.
Absolute Maxima na Minima
- upeo kabisa wa\(f\) saa\(x=c\) ni\(f(c)\) wapi\(f(c)≥f(x)\) kwa wote\(x\) katika uwanja wa\(f\).
- kiwango cha chini kabisa cha\(f\) saa\(x=d\) ni\(f(d)\) wapi\(f(d)≤f(x)\) kwa wote\(x\) katika uwanja wa\(f\).
Mfano\(\PageIndex{10}\): Finding Absolute Maxima and Minima from a Graph
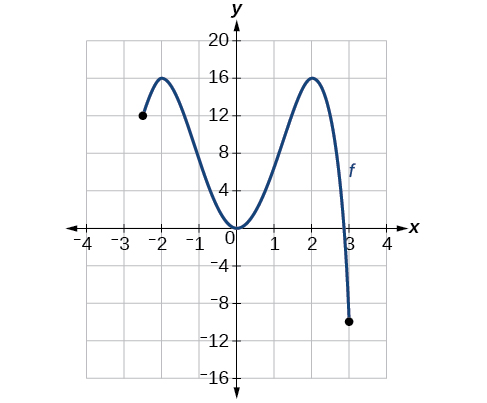
Kwa kazi ya inavyoonekana kwenye Kielelezo\(\PageIndex{14}\), pata kiwango cha juu kabisa na cha chini.
Suluhisho
Kuzingatia grafu ya\(f\). Grafu inafikia kiwango cha juu kabisa katika maeneo mawili,\(x=−2\) na\(x=2\), kwa sababu katika maeneo haya, grafu inafikia hatua yake ya juu juu ya uwanja wa kazi. Upeo kabisa ni kuratibu y\(x=−2\) na\(x=2\), ambayo ni 16.
Grafu inafikia kiwango cha chini kabisa katika x=3, kwa sababu ni hatua ya chini kabisa kwenye uwanja wa grafu ya kazi. Kiwango cha chini kabisa ni kuratibu y katika x=3, ambayo ni-10.
Mlinganyo muhimu
- Wastani wa kiwango cha mabadiliko:\(\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\)
Dhana muhimu
- Kiwango cha mabadiliko kinahusiana na mabadiliko katika wingi wa pato na mabadiliko katika kiasi cha pembejeo. Kiwango cha wastani cha mabadiliko kinatambuliwa kutumia tu data ya mwanzo na ya mwisho. Angalia Mfano.
- Kutambua pointi zinazoashiria muda kwenye grafu zinaweza kutumika kupata kiwango cha wastani cha mabadiliko. Angalia Mfano.
- Kulinganisha jozi ya maadili ya pembejeo na pato katika meza pia inaweza kutumika kupata kiwango cha wastani cha mabadiliko. Angalia Mfano.
- Kiwango cha wastani cha mabadiliko kinaweza pia kuhesabiwa kwa kuamua maadili ya kazi kwenye mwisho wa kipindi kilichoelezwa na formula. Angalia Mfano na Mfano.
- Kiwango cha wastani cha mabadiliko wakati mwingine kinaweza kuamua kama kujieleza. Angalia Mfano.
- Kazi inaongezeka ambapo kiwango chake cha mabadiliko ni chanya na kupungua ambapo kiwango chake cha mabadiliko ni hasi. Angalia Mfano.
- Upeo wa ndani ni pale ambapo kazi inabadilika kuongezeka hadi kupungua na ina thamani ya pato kubwa (chanya zaidi au chini hasi) kuliko maadili ya pato katika maadili ya pembejeo jirani.
- Kiwango cha chini cha ndani ni pale ambapo kazi inabadilika kutoka kupungua hadi kuongezeka (kama ongezeko la pembejeo) na ina thamani ya pato ndogo (hasi zaidi au chini ya chanya) kuliko maadili ya pato katika maadili ya pembejeo ya jirani.
- Minima na maxima pia huitwa extrema.
- Tunaweza kupata extrema mitaa kutoka grafu. Angalia Mfano na Mfano.
- Pointi ya juu na ya chini zaidi kwenye grafu zinaonyesha maxima na minima. Angalia Mfano.


