1.5: Mabadiliko ya Kazi

Last updated
Save as PDF

Page ID: 181181

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Kazi za Grafu kwa kutumia mabadiliko ya wima na ya usawa.
Graph kazi kwa kutumia tafakari kuhusu x-axis na y-axis.
Kuamua kama kazi ni hata, isiyo ya kawaida, au wala kutoka kwenye grafu yake.
Graph kazi kwa kutumia compressions na stretches.
Kuchanganya mabadiliko.

Sisi sote tunajua kwamba kioo gorofa inatuwezesha kuona picha sahihi ya sisi wenyewe na chochote kilicho nyuma yetu. Tunapotengeneza kioo, picha tunazoona zinaweza kuhama kwa usawa au kwa wima. Lakini nini kinatokea wakati sisi bend kioo rahisi? Kama kioo cha funhouse cha carnival, kinatupa picha iliyopotoka ya sisi wenyewe, imetambulishwa au imesisitizwa kwa usawa au kwa wima. Kwa namna hiyo, tunaweza kupotosha au kubadilisha kazi za hisabati ili kuzibadilisha vizuri kuelezea vitu au michakato katika ulimwengu halisi. Katika sehemu hii, tutaangalia aina kadhaa za mabadiliko.

alt — Kielelezo$\PageIndex{1}$: (mikopo: “Misko” /Flickr)

Mara nyingi tunapopewa tatizo, tunajaribu kutengeneza hali hiyo kwa kutumia hisabati kwa namna ya maneno, meza, grafu, na equations. Njia moja tunaweza kuajiri ni kukabiliana na grafu za msingi za kazi za toolkit ili kujenga mifano mpya kwa hali fulani. Kuna njia za utaratibu wa kubadilisha kazi ili kujenga mifano sahihi kwa matatizo tunayojaribu kutatua.

Kutambua Mabadiliko ya Wima

Aina moja rahisi ya mabadiliko inahusisha kuhama grafu nzima ya kazi juu, chini, kulia, au kushoto. Mabadiliko rahisi ni mabadiliko ya wima, kusonga grafu juu au chini, kwa sababu mabadiliko haya yanahusisha kuongeza mara kwa mara chanya au hasi kwa kazi. Kwa maneno mengine, tunaongeza mara kwa mara sawa na thamani ya pato ya kazi bila kujali pembejeo. Kwa kazi$g(x)=f(x)+k$, kazi$f(x)$ ni kubadilishwa$k$ vitengo wima. Angalia Kielelezo$\PageIndex{2}$ kwa mfano.

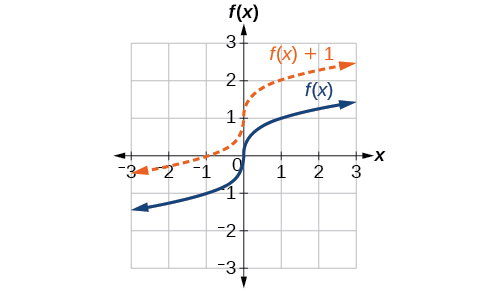
Kubadilisha wima kwa k=1 ya kazi ya mizizi ya mchemraba f (x) =3√x. — Kielelezo$\PageIndex{2}$: Wima kuhama na$k=1$ ya mchemraba mizizi kazi$f(x)=\sqrt[3]{x}$.

Ili kukusaidia kutazama dhana ya mabadiliko ya wima, fikiria hilo$y=f(x)$. Kwa hiyo,$f(x)+k$ ni sawa na$y+k$. Kila kitengo cha$y$ ni kubadilishwa na$y+k$, hivyo$y$ -thamani kuongezeka au itapungua kulingana na thamani ya$k$. Matokeo yake ni mabadiliko ya juu au chini.

Ufafanuzi: Shift Wima

Kutokana na kazi$f(x)$, kazi mpya$g(x)=f(x)+k$, ambapo$k$ ni mara kwa mara, ni mabadiliko ya wima ya kazi$f(x)$. Maadili yote ya pato hubadilika na$k$ vitengo. Ikiwa$k$ ni chanya, grafu itaondoka. Ikiwa$k$ ni hasi, grafu itashuka.

Mfano$\PageIndex{1}$: Adding a Constant to a Function

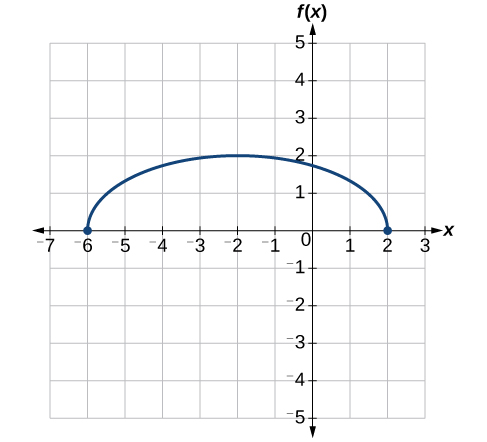
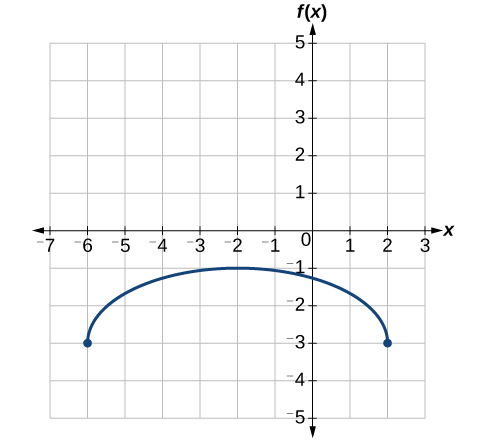
Ili kudhibiti joto katika jengo la kijani, vents ya hewa karibu na paa wazi na karibu siku nzima. Kielelezo$\PageIndex{3}$ kinaonyesha eneo la matundu ya wazi$V$ (katika miguu ya mraba) siku nzima katika masaa baada ya usiku wa manane,$t$. Wakati wa majira ya joto, meneja wa vifaa huamua kujaribu kudhibiti hali ya joto kwa kuongeza kiasi cha matundu ya wazi kwa futi za mraba 20 mchana na usiku. Mchoro grafu ya kazi hii mpya.

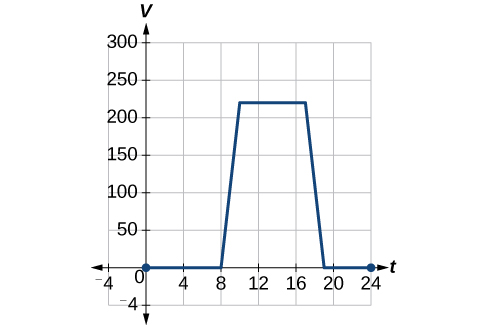
Suluhisho

Tunaweza mchoro grafu ya kazi hii mpya kwa kuongeza 20 kwa kila moja ya maadili ya pato ya kazi ya awali. Hii itakuwa na athari ya kugeuza grafu kwa wima, kama inavyoonekana kwenye Kielelezo$\PageIndex{4}$.

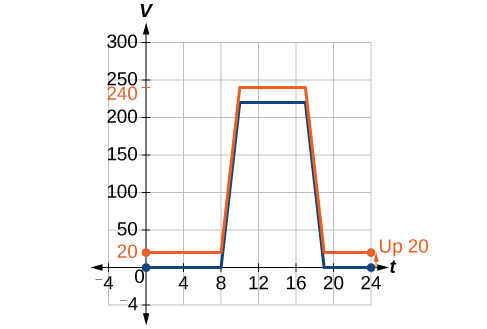
Kumbuka kwamba katika Kielelezo$\PageIndex{4}$, kwa thamani ya kila pembejeo, thamani ya pato imeongezeka kwa 20, hivyo kama sisi wito kazi mpya$S(t)$, tunaweza kuandika

\[S(t)=V(t)+20\]

Nukuu hii inatuambia kwamba, kwa thamani yoyote ya$t$,$S(t)$ inaweza kupatikana kwa kutathmini kazi$V$ katika pembejeo sawa na kisha kuongeza 20 kwa matokeo. Hii inafafanua$S$ kama mabadiliko ya kazi$V$, katika kesi hii kuhama wima hadi 20 vitengo. Angalia kwamba, kwa mabadiliko ya wima, maadili ya pembejeo hukaa sawa na maadili ya pato tu yanabadilika. Angalia Jedwali$\PageIndex{1}$.

Jedwali$\PageIndex{1}$
$t$	0	8	10	17	19	24
$V(t)$	0	0	220	220	0	0
$S(t)$	20	20	240	240	20	20

Jinsi ya...

Kutokana na kazi ya tabular, tengeneza mstari mpya ili kuwakilisha mabadiliko ya wima.

Tambua mstari wa pato au safu.
Kuamua ukubwa wa mabadiliko.
Ongeza mabadiliko kwa thamani katika kila kiini cha pato. Kuongeza thamani chanya kwa ajili ya juu au thamani hasi kwa chini.

Mfano$\PageIndex{2}$: Shifting a Tabular Function Vertically

Kazi$f(x)$ hutolewa katika Jedwali$\PageIndex{2}$. Unda meza kwa kazi$g(x)=f(x)−3$.

Jedwali$\PageIndex{2}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Suluhisho

formula$g(x)=f(x)−3$ inatuambia kwamba tunaweza kupata maadili pato la$g$ kwa kutoa 3 kutoka maadili pato la$f$. Kwa mfano:

\[\begin{align*} f(x)&=1 &\text{Given} \\[4pt] g(x)&=f(x)-3 &\text{Given Transformation} \\[4pt] g(2) & =f(2)−3 \\ &=1-3\\ &=-2\end{align*}\]

Kutoa 3 kutoka kila$f(x)$ thamani, tunaweza kukamilisha meza ya maadili kwa$g(x)$ kama inavyoonekana katika Jedwali$\PageIndex{3}$.

Jedwali$\PageIndex{3}$
$x$	2	4	6	8
$f(x)$	1	3	7	11
$g(x)$	-2	0	4	8

Uchambuzi

Kama ilivyo kwa mabadiliko ya awali ya wima, angalia maadili ya pembejeo yanafanana na maadili ya pato tu yanabadilika.

Zoezi$\PageIndex{1}$

Kazi$h(t)=−4.9t^2+30t$ hutoa urefu$h$ wa mpira (katika mita) kutupwa juu kutoka chini baada ya$t$ sekunde. Tuseme mpira ilikuwa badala kutupwa kutoka juu ya jengo 10-m. Kuhusiana hii mpya urefu kazi$b(t)$ kwa$h(t)$, na kisha kupata formula kwa$b(t)$.

Jibu: $b(t)=h(t)+10=−4.9t^2+30t+10$

Kutambua Mabadiliko ya Ulalo

Tuliona tu kwamba mabadiliko ya wima ni mabadiliko ya pato, au nje, ya kazi. Sasa tutaangalia jinsi mabadiliko ya pembejeo, ndani ya kazi, kubadilisha grafu yake na maana. Kuhama kwa matokeo ya pembejeo katika harakati ya grafu ya kazi kushoto au kulia katika kile kinachojulikana kama mabadiliko ya usawa, inavyoonekana katika Kielelezo$\PageIndex{4}$.

alt — Kielelezo$\PageIndex{4}$: Kuhama kwa usawa wa kazi$f(x)=\sqrt[3]{x}$. Kumbuka kuwa$h=-1$ mabadiliko grafu upande wa kushoto, yaani, kuelekea maadili hasi ya$x$.

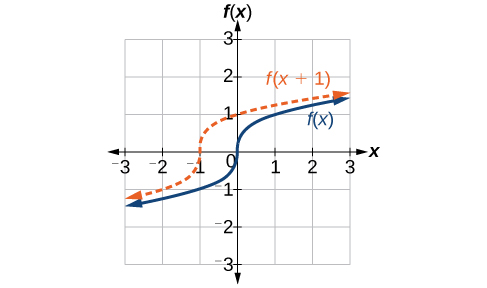
Kwa mfano, ikiwa$f(x)=x^2$, basi$g(x)=(x−2)^2$ ni kazi mpya. Kila pembejeo ni kupunguzwa kwa 2 kabla ya squaring kazi. Matokeo yake ni kwamba grafu inabadilishwa vitengo 2 kwa haki, kwa sababu tunahitaji kuongeza pembejeo kabla na vitengo 2 ili kutoa thamani sawa ya pato kama ilivyoelezwa$f$.

Ufafanuzi: Shift ya usawa

Kutokana na kazi$f$, kazi mpya$g(x)=f(x−h)$, ambapo$h$ ni mara kwa mara, ni mabadiliko ya usawa ya kazi$f$. Ikiwa$h$ ni chanya, grafu itabadilika haki. Ikiwa$h$ ni hasi, grafu itabadilika kushoto.

Mfano$\PageIndex{4}$: Adding a Constant to an Input

Kurudi kwa jengo wetu airflow mfano kutoka Kielelezo$\PageIndex{2}$, tuseme kwamba katika vuli meneja vifaa anaamua kwamba awali venting mpango kuanza kuchelewa mno, na anataka kuanza nzima venting mpango 2 masaa mapema. Mchoro grafu ya kazi mpya.

Suluhisho

Tunaweza$V(t)$ kuweka kuwa mpango wa awali$F(t)$ na kuwa mpango upya.

\[V(t)= \text{ the original venting plan} \nonumber\]

\[F(t)= \text{ starting 2 hrs sooner} \nonumber\]

Katika grafu mpya, kila wakati, hewa ya hewa ni sawa na kazi ya awali$V$ ilikuwa masaa 2 baadaye. Kwa mfano, katika kazi ya awali$V$, airflow huanza kubadilika saa 8 a.m.$F$, ambapo kwa kazi, airflow huanza kubadilika saa 6 a.m$V(8)=F(6)$. Angalia Kielelezo$\PageIndex{5}$. Angalia pia kwamba matundu yalifunguliwa kwanza$220 \text{ft}^2$ saa 10 asubuhi chini ya mpango wa awali, wakati chini ya mpango mpya matundu yanafikia$220 \text{ft}^2$ saa 8 asubuhi, hivyo$V(10)=F(8)$.

Katika hali zote mbili, tunaona kwamba, kwa sababu$F(t)$ kuanza saa 2 mapema,$h=−2$. Hiyo ina maana kwamba maadili sawa pato ni kufikiwa wakati$F(t)=V(t−(−2))=V(t+2)$.

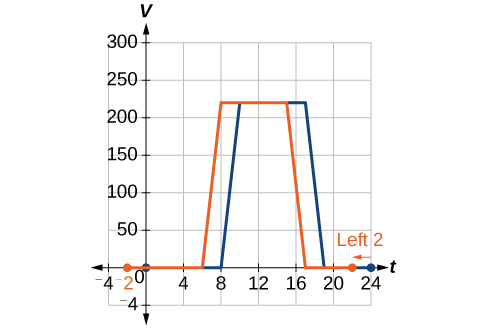
Uchambuzi

Kumbuka kuwa$V(t+2)$ ina athari ya kuhama grafu upande wa kushoto.

Mabadiliko ya usawa au “mabadiliko ya ndani” huathiri uwanja wa kazi (pembejeo) badala ya upeo na mara nyingi huonekana kuwa kinyume. Kazi mpya$F(t)$ inatumia matokeo sawa na$V(t)$, lakini inafanana na matokeo hayo kwa pembejeo 2 masaa mapema kuliko yale ya$V(t)$. Alisema njia nyingine, ni lazima kuongeza 2 masaa ya pembejeo ya$V$ kupata pato sambamba kwa$F:F(t)=V(t+2)$.

Jinsi ya...

Kutokana na kazi ya tabular, tengeneza mstari mpya ili kuwakilisha mabadiliko ya usawa.

Tambua mstari wa pembejeo au safu.
Kuamua ukubwa wa mabadiliko.
Ongeza mabadiliko kwa thamani katika kila kiini cha pembejeo.

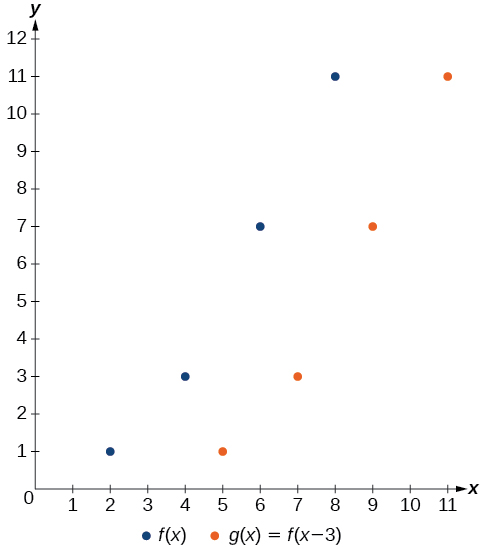
Mfano$\PageIndex{5}$: Shifting a Tabular Function Horizontally

Kazi$f(x)$ hutolewa katika Jedwali$\PageIndex{4}$. Unda meza kwa kazi$g(x)=f(x−3)$.

Jedwali$\PageIndex{4}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Suluhisho

formula$g(x)=f(x−3)$ inatuambia kwamba maadili pato ya$g$ ni sawa na thamani ya pato la$f$ wakati thamani pembejeo ni 3 chini ya thamani ya awali. Kwa mfano, tunajua hilo$f(2)=1$. Ili kupata pato sawa kutoka kwa kazi$g$, tutahitaji thamani ya pembejeo ambayo ni 3 kubwa. Sisi pembejeo thamani kwamba ni 3 kubwa kwa$g(x)$ sababu kazi inachukua 3 mbali kabla ya kutathmini kazi$f$.

\[\begin{align*} g(5)&=f(5-3) \\ &=f(2) \\ &=1 \end{align*}\]

Tunaendelea na maadili mengine ili kuunda Jedwali$\PageIndex{5}$.

Jedwali$\PageIndex{5}$
$x$	5	7	9	11
$x-3$	2	4	6	8
$f(x)$	1	3	7	11
$g(x)$	1	3	7	11

Matokeo yake ni kwamba kazi$g(x)$ imebadilishwa kwa haki na 3. Angalia maadili ya pato kwa$g(x)$ kubaki sawa na maadili ya pato kwa$f(x)$, lakini maadili sambamba pembejeo$x$, kuwa kubadilishwa na haki kwa 3. Hasa, 2 kubadilishwa kwa 5, 4 kubadilishwa kwa 7, 6 kubadilishwa kwa 9, na 8 kubadilishwa kwa 11.

Uchambuzi

Kielelezo$\PageIndex{6}$ inawakilisha kazi zote mbili. Tunaweza kuona mabadiliko ya usawa katika kila hatua.

Grafu ya pointi kutoka meza ya awali kwa f (x) na g (x) =f (x-3) — Kielelezo$\PageIndex{6}$: Grafu ya pointi kutoka meza ya awali kwa$f(x)$ na$g(x)=f(x-3)$

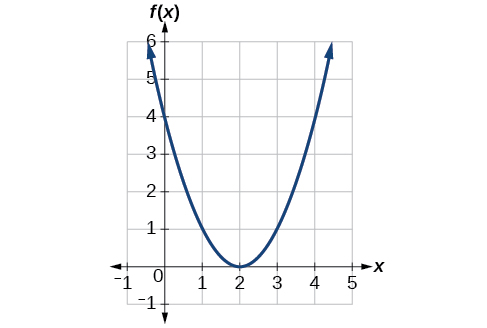
Mfano$\PageIndex{6}$: Identifying a Horizontal Shift of a Toolkit Function

Kielelezo$\PageIndex{7}$ inawakilisha mabadiliko ya kazi ya toolkit$f(x)=x^2$. Kuhusiana kazi hii mpya$g(x)$ kwa$f(x)$, na kisha kupata formula kwa$g(x)$.

Kielelezo$\PageIndex{7}$: Grafu ya parabola

Suluhisho

Angalia kwamba grafu inafanana na sura ya$f(x)=x^2$ kazi, lakini$x$ maadili ya -yanabadilishwa kwenye vitengo 2 vya haki. Vertex kutumika kuwa katika$(0,0)$, lakini sasa kipeo ni saa$(2,0)$. Grafu ni kazi ya msingi ya quadratic iliyobadilishwa vitengo 2 kwa haki, hivyo

\[g(x)=f(x−2) \nonumber\]

Angalia jinsi ni lazima pembejeo thamani ya$x=2$ kupata thamani ya pato$y=0$;$x$ -maadili lazima 2 vitengo kubwa kwa sababu ya mabadiliko ya haki kwa 2 vitengo. Tunaweza kisha kutumia ufafanuzi wa$f(x)$ kazi ya kuandika formula$g(x)$ kwa kutathmini$f(x−2)$.

\[\begin{align*} f(x)&=x^2 \\ g(x)&=f(x-2) \\ g(x)&=f(x-2)=(x-2)^2 \end{align*}\]

Uchambuzi

Kuamua kama mabadiliko ni$+2$ au$−2$, fikiria hatua moja ya kumbukumbu kwenye grafu. Kwa quadratic, kuangalia hatua ya vertex ni rahisi. Katika kazi ya awali,$f(0)=0$. Katika kazi yetu iliyobadilishwa,$g(2)=0$. Ili kupata thamani ya pato ya 0 kutoka kwa kazi$f$, tunahitaji kuamua kama ishara ya pamoja au minus itafanya kazi ili kukidhi$g(2)=f(x−2)=f(0)=0$. Ili kufanya kazi hii, tutahitaji kuondoa vitengo 2 kutoka kwa maadili yetu ya pembejeo.

Mfano$\PageIndex{7}$: Interpreting Horizontal versus Vertical Shifts

Kazi hiyo$G(m)$ inatoa idadi ya galoni za gesi zinazohitajika kuendesha$m$ maili. Tafsiri$G(m)+10$ na$G(m+10)$

Suluhisho

$G(m)+10$inaweza kutafsiriwa kama kuongeza 10 kwa pato, galoni. Hii ni gesi inayotakiwa kuendesha$m$ maili, pamoja na galoni nyingine 10 za gesi. Grafu ingeonyesha mabadiliko ya wima.

$G(m+10)$inaweza kutafsiriwa kama kuongeza 10 kwa pembejeo, maili. Hivyo hii ni idadi ya galoni za gesi zinazohitajika kuendesha maili 10 zaidi ya$m$ maili. Grafu ingeonyesha mabadiliko ya usawa.

Zoezi$\PageIndex{7}$

Kutokana na kazi$f(x)=\sqrt{x}$, graph kazi ya awali$f(x)$ na mabadiliko$g(x)=f(x+2)$ kwenye axes sawa. Je! Hii ni mabadiliko ya usawa au wima? Njia gani grafu imebadilishwa na kwa vitengo ngapi?

Jibu: Grafu za$f(x)$ na$g(x)$ zinaonyeshwa hapa chini. Mabadiliko ni mabadiliko ya usawa. Kazi inabadilishwa upande wa kushoto na vitengo 2.

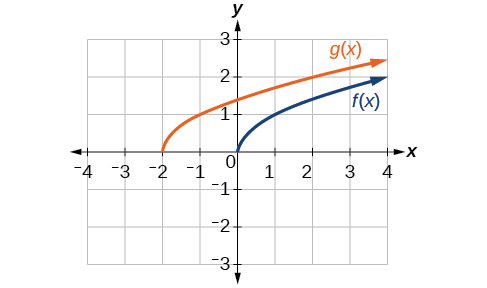
$Grafu ya kazi ya mizizi ya mraba na kazi ya mguu wa mraba ya kuhama kwa usawa.$
Kielelezo$\PageIndex{8}$

Kuchanganya Mabadiliko ya Wima na ya usawa

Sasa kwa kuwa tuna mabadiliko mawili, tunaweza kuchanganya pamoja. Mabadiliko ya wima ni nje ya mabadiliko yanayoathiri maadili ya$(y-)$ mhimili wa pato na kuhama kazi juu au chini. Mabadiliko ya usawa ni ndani ya mabadiliko yanayoathiri maadili ya$(x-)$ mhimili wa pembejeo na kuhama kazi kushoto au kulia. Kuchanganya aina mbili za mabadiliko itasababisha grafu ya kazi kuhama juu au chini na kulia au kushoto.

Jinsi ya...

Kutokana na kazi na mabadiliko ya wima na ya usawa, mchoro grafu.

Tambua mabadiliko ya wima na ya usawa kutoka kwa formula.
Mabadiliko ya wima yanatokana na mara kwa mara aliongeza kwa pato. Hoja grafu hadi kwa mara kwa mara chanya na chini kwa mara hasi.
Mabadiliko ya usawa yanatokana na mara kwa mara iliyoongezwa kwa pembejeo. Hoja grafu kushoto kwa mara kwa mara chanya na haki kwa mara kwa mara hasi.
Tumia mabadiliko kwenye grafu kwa utaratibu wowote.

Mfano$\PageIndex{8}$: Graphing Combined Vertical and Horizontal Shifts

kutokana$f(x)=|x|$, mchoro grafu ya$h(x)=f(x+1)−3$.

Suluhisho

kazi$f$ ni toolkit yetu kabisa thamani kazi. Tunajua kwamba grafu hii ina sura ya V, na uhakika wa asili. Grafu ya$h$ imebadilishwa$f$ kwa njia mbili:$f(x+1)$ ni mabadiliko ndani ya kazi, kutoa mabadiliko ya usawa kushoto na 1, na kutoa kwa 3 in$f(x+1)−3$ ni mabadiliko kwa nje ya kazi, kutoa mabadiliko ya wima chini kwa 3. Mabadiliko ya grafu yanaonyeshwa kwenye Kielelezo$\PageIndex{9}$.

Hebu kufuata hatua moja ya grafu ya$f(x)=|x|$.

Hatua hiyo$(0,0)$ inabadilishwa kwanza kwa kuhama kitengo cha kushoto 1:$(0,0)\rightarrow(−1,0)$
Hatua hiyo$(−1,0)$ inabadilishwa ijayo na kuhama chini vitengo 3:$(−1,0)\rightarrow(−1,−3)$

Grafu ya kazi kamili, <span tafsiri = — Kielelezo$\PageIndex{9}$: Grafu ya kazi kamili$y=|x|$,, na jinsi ilibadilishwa$y=|x+1|-3$

Kielelezo$\PageIndex{10}$ inaonyesha grafu ya$h$.

Kazi ya mwisho <span tafsiri = — Kielelezo$\PageIndex{10}$: Kazi ya mwisho$y=|x+1|-3$.

Zoezi$\PageIndex{8}$

kutokana$f(x)=|x|$, mchoro grafu ya$h(x)=f(x−2)+4$.

Jibu: $alt$
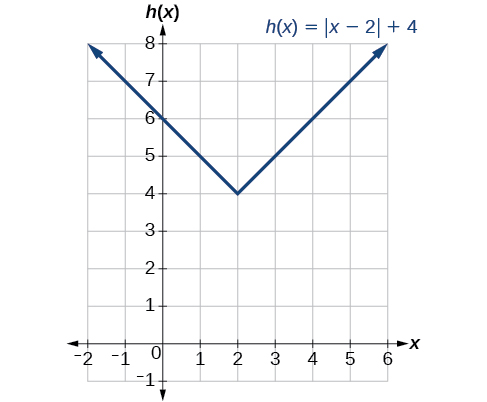
Kielelezo$\PageIndex{11}$

Mfano$\PageIndex{9}$: Identifying Combined Vertical and Horizontal Shifts

Andika formula kwa grafu iliyoonyeshwa kwenye Kielelezo$\PageIndex{12}$, ambayo ni mabadiliko ya kazi ya mizizi ya mraba ya toolkit.

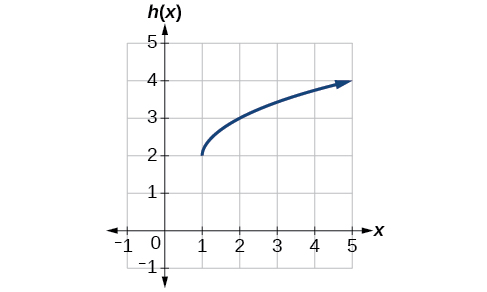
Grafu ya kazi ya mizizi mraba transposed haki kitengo kimoja kuendelea 2. — Kielelezo$\PageIndex{12}$: Grafu ya kazi ya mizizi ya mraba transposed haki kitengo kimoja kuendelea 2.

Suluhisho

Grafu ya kazi ya toolkit huanza kwa asili, hivyo grafu hii imebadilishwa 1 kwa haki na juu 2. Katika kazi nukuu, tunaweza kuandika kwamba kama

\[h(x)=f(x−1)+2 \nonumber\]

Kutumia formula ya kazi ya mizizi ya mraba, tunaweza kuandika

\[h(x)=\sqrt{x−1}+2 \nonumber\]

Uchambuzi

Kumbuka kuwa mabadiliko haya yamebadilika uwanja na aina mbalimbali za kazi. Grafu hii mpya ina uwanja$\left[1,\infty\right)$ na upeo$\left[2,\infty\right)$.

Zoezi$\PageIndex{9}$

Andika formula kwa ajili ya mabadiliko ya toolkit kazi kubadilishwa$f(x)=\frac{1}{x}$ kwamba mabadiliko ya kazi ya graph kitengo moja na haki na kitengo kimoja juu.

Jibu: \[g(x)=\dfrac{1}{x-1}+1 \nonumber \]

Kazi za kuchora Kutumia Tafakari kuhusu Axes

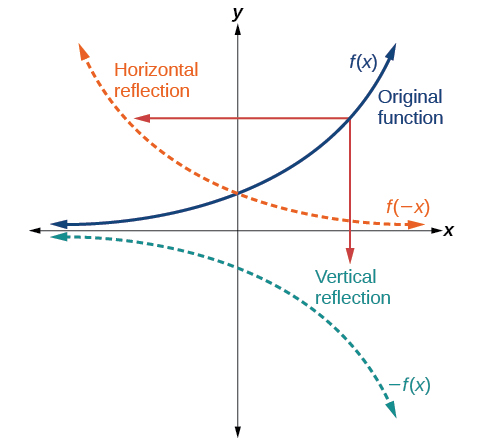
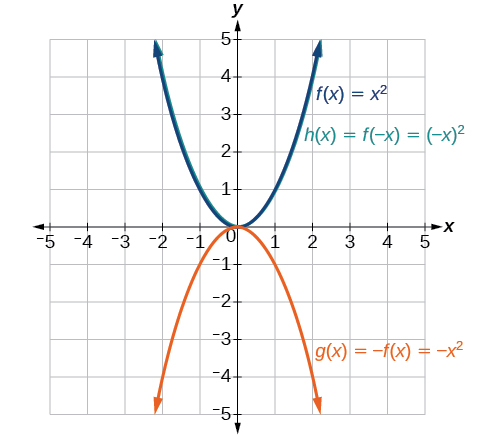
Mabadiliko mengine ambayo yanaweza kutumika kwa kazi ni tafakari juu ya x- au y-mhimili. Kutafakari kwa wima huonyesha grafu kwa wima kwenye mhimili wa x-axis, wakati kutafakari kwa usawa kunaonyesha grafu kwa usawa kwenye mhimili wa y. tafakari ni inavyoonekana katika Kielelezo$\PageIndex{13}$.

Kielelezo$\PageIndex{13}$: Grafu ya kutafakari wima na usawa wa kazi.

Angalia kwamba kutafakari wima hutoa grafu mpya ambayo ni picha ya kioo ya msingi au grafu ya awali kuhusu x-axis. Kutafakari kwa usawa hutoa grafu mpya ambayo ni picha ya kioo ya grafu ya msingi au ya awali kuhusu mhimili wa y.

ufafanuzi: Tafakari

Kutokana na kazi$f(x)$, kazi mpya$g(x)=−f(x)$ ni kutafakari wima ya kazi$f(x)$, wakati mwingine huitwa kutafakari kuhusu (au juu, au kupitia) x-axis.

Kutokana na kazi$f(x)$, kazi mpya$g(x)=f(−x)$ ni kutafakari kwa usawa wa kazi$f(x)$, wakati mwingine huitwa kutafakari kuhusu mhimili wa y.

Jinsi ya...

Kutokana na kazi, kutafakari grafu wote kwa wima na usawa.

Kuzidisha matokeo yote kwa -1 kwa kutafakari wima. Grafu mpya ni mfano wa grafu ya awali kuhusu x-axis.
Panua pembejeo zote kwa -1 kwa kutafakari kwa usawa. Grafu mpya ni mfano wa grafu ya awali kuhusu mhimili wa y.

Mfano$\PageIndex{10}$: Reflecting a Graph Horizontally and Vertically

Fikiria grafu ya$s(t)=\sqrt{t}$ (a) kwa wima na (b) kwa usawa.

Suluhisho

a. kutafakari grafu wima ina maana kwamba kila thamani pato itakuwa yalijitokeza juu ya usawa t-mhimili kama inavyoonekana katika Kielelezo$\PageIndex{14}$.

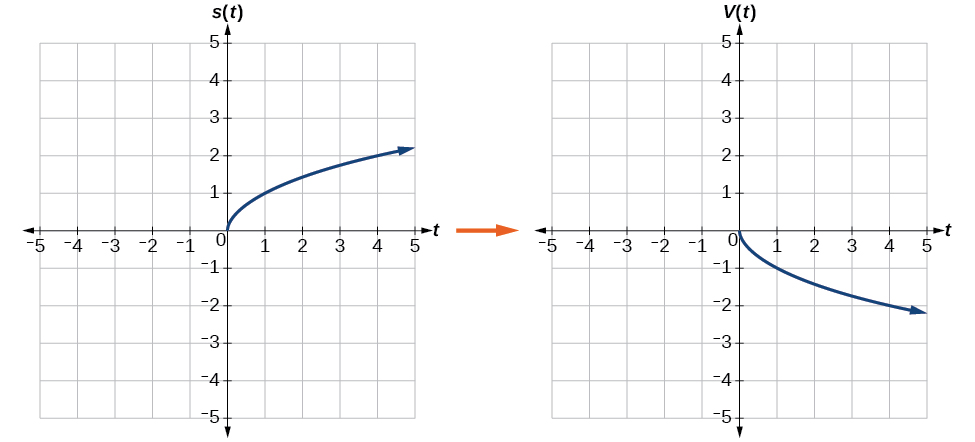
Kielelezo$\PageIndex{14}$: Grafu ya kutafakari wima ya kazi ya mizizi ya mraba.

Kwa sababu kila thamani ya pato ni kinyume cha thamani ya awali ya pato, tunaweza kuandika

\[V(t)=−s(t) \text{ or } V(t)=−\sqrt{t} \nonumber\]

Kumbuka kwamba hii ni mabadiliko ya nje, au mabadiliko ya wima, ambayo huathiri$s(t)$ maadili ya pato, hivyo ishara hasi ni nje ya kazi.

b Kuonyesha usawa ina maana kwamba kila thamani pembejeo itakuwa yalijitokeza juu ya mhimili wima kama inavyoonekana katika Kielelezo$\PageIndex{15}$.

Grafu ya kutafakari usawa wa kazi ya mizizi ya mraba. — Kielelezo$\PageIndex{15}$: Kutafakari kwa usawa wa kazi ya mizizi ya mraba

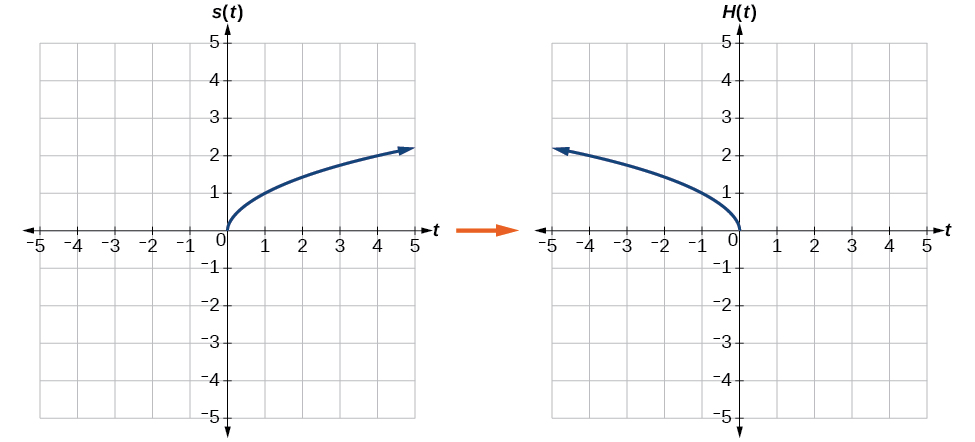
Kwa sababu kila thamani ya pembejeo ni kinyume cha thamani ya awali ya pembejeo, tunaweza kuandika

\[H(t)=s(−t) \text{ or } H(t)=\sqrt{−t} \nonumber\]

Kumbuka kwamba hii ni mabadiliko ya ndani au mabadiliko ya usawa ambayo huathiri maadili ya pembejeo, hivyo ishara hasi iko ndani ya kazi.

Kumbuka kuwa mabadiliko haya yanaweza kuathiri uwanja na kazi mbalimbali. Wakati kazi ya mizizi ya mraba ya awali ina kikoa$\left[0,\infty\right)$ na upeo$\left[0,\infty\right)$, kutafakari kwa wima kunatoa$V(t)$ kazi mbalimbali$\left(−\infty,0\right]$ na kutafakari kwa usawa kunatoa$H(t)$ kazi uwanja$\left(−\infty, 0\right]$.

Zoezi$\PageIndex{5}$

Fikiria grafu ya$f(x)=|x−1|$ (a) kwa wima na (b) kwa usawa.

Jibu

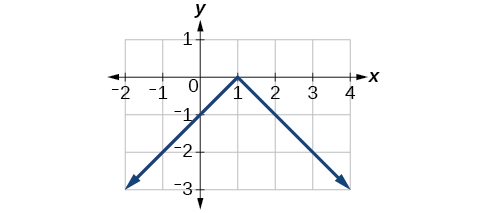
Kielelezo$\PageIndex{16}$: Grafu ya kazi kamili iliyojitokeza kwa wima.

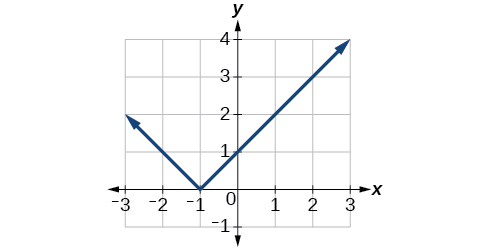
Grafu ya kazi kamili kutafsiriwa kitengo kimoja kilichoachwa. — Kielelezo$\PageIndex{17}$: Grafu ya kazi kamili kutafsiriwa kitengo kimoja kushoto.

Mfano$\PageIndex{11}$: Reflecting a Tabular Function Horizontally and Vertically

Kazi$f(x)$ inapewa kama Jedwali$\PageIndex{6}$. Unda meza kwa ajili ya kazi hapa chini.

a.$g(x)=−f(x)$
b.$h(x)=f(−x)$

Jedwali$\PageIndex{6}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

a Kwa$g(x)$, ishara hasi nje ya kazi inaonyesha kutafakari wima, hivyo maadili ya x hukaa sawa na kila thamani ya pato itakuwa kinyume na thamani ya awali ya pato. Angalia Jedwali$\PageIndex{7}$.

Jedwali$\PageIndex{7}$
$x$	2	4	6	8
$g(x)$	-1	-3	-7	-11

b Kwa$h(x)$, ishara hasi ndani ya kazi inaonyesha kutafakari usawa, hivyo kila thamani ya pembejeo itakuwa kinyume na thamani ya awali ya pembejeo na$h(x)$ maadili hukaa sawa na$f(x)$ maadili. Angalia Jedwali$\PageIndex{8}$.

Jedwali$\PageIndex{8}$
$x$	-2	-4	-6	-8
$h(x)$	1	3	7	11

Zoezi$\PageIndex{6}$

Kazi$f(x)$ inapewa kama Jedwali$\PageIndex{9}$. Unda meza kwa ajili ya kazi hapa chini.

a.$g(x)=−f(x)$
b.$h(x)=f(−x)$

Jedwali$\PageIndex{9}$
$x$	-2	0	2	4
$f(x)$	5	10	15	20

Jibu

a.$g(x)=−f(x)$

Jedwali$\PageIndex{10}$
$x$	-2	0	2	4
$g(x)$	-5	-10	-15	-20

b.$h(x)=f(−x)$

Jedwali$\PageIndex{11}$
$x$	-2	0	2	-4
$h(x)$	15	10	5	20

Mfano$\PageIndex{12}$: Applying a Learning Model Equation

Mfano wa kawaida wa kujifunza una equation sawa na$k(t)=−2^{−t}+1$,$k$ wapi asilimia ya ustadi ambayo inaweza kupatikana baada ya vikao vya$t$ mazoezi. Hii ni mabadiliko ya kazi$f(t)=2^t$ iliyoonyeshwa kwenye Kielelezo$\PageIndex{18}$. Mchoro grafu ya$k(t)$.

Grafu ya <span tafsiri = — Kielelezo$\PageIndex{18}$: Grafu ya$k(t)$

Suluhisho

Equation hii inachanganya mabadiliko matatu katika equation moja.

Kutafakari kwa usawa:$f(−t)=2^{−t}$
Kutafakari wima:$−f(−t)=−2^{−t}$
Mabadiliko ya wima:$−f(−t)+1=−2^{−t}+1$

Tunaweza kuchora grafu kwa kutumia mabadiliko haya moja kwa wakati kwa kazi ya awali. Hebu tufuate pointi mbili kupitia kila moja ya mabadiliko matatu. Tutachagua pointi$(0, 1)$ na$(1, 2)$.

Kwanza, tunatumia kutafakari usawa:$(0, 1) \; (–1, 2)$.
Kisha, tunatumia kutafakari wima:$(0, −1) \; (-1, –2)$.
Hatimaye, tunatumia mabadiliko ya wima:$(0, 0) \; (-1, -1)$.

Hii ina maana kwamba pointi ya awali,$(0,1)$$(0,0)$ na$(1,2)$ kuwa na$(-1,-1)$ baada ya sisi kutumia mabadiliko.

Katika Kielelezo$\PageIndex{19}$, grafu ya kwanza inatokana na kutafakari kwa usawa. Matokeo ya pili kutoka kwa kutafakari wima. matokeo ya tatu kutoka kuhama wima hadi 1 kitengo.

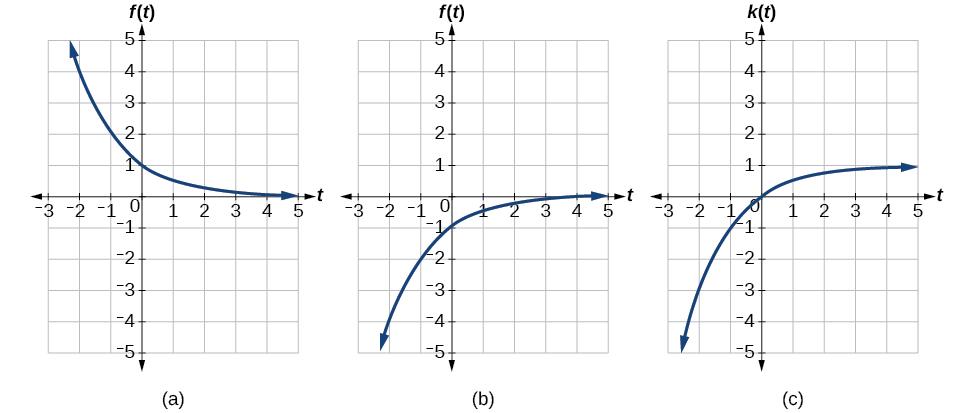
Kielelezo$\PageIndex{19}$: Grafu ya mabadiliko yote.

Uchambuzi

Kama mfano wa kujifunza, kazi hii itakuwa mdogo kwa uwanja wa$t\geq0$, na aina sambamba$\left[0,1\right)$.

Zoezi$\PageIndex{7}$

Kutokana na kazi ya toolkit$f(x)=x^2$, grafu$g(x)=−f(x)$ na$h(x)=f(−x)$. Kumbuka tabia yoyote ya kushangaza kwa kazi hizi.

Jibu: $Grafu ya x ^ 2 na tafakari zake.$
Kielelezo$\PageIndex{20}$: Grafu ya$x^2$ na tafakari zake.

Taarifa:$g(x)=f(−x)$ inaonekana sawa na$f(x)$.

Kuamua Kazi Hata na isiyo ya kawaida

Baadhi ya kazi zinaonyesha ulinganifu ili tafakari zipate grafu ya awali. Kwa mfano, kwa usawa kutafakari kazi za toolkit$f(x)=x^2$ au$f(x)=|x|$ itasababisha grafu ya awali. Tunasema kwamba aina hizi za grafu zinalingana kuhusu mhimili wa y. Kazi ambazo grafu zinalingana kuhusu mhimili wa y huitwa hata kazi.

Kama grafu ya$f(x)=x^3$ au$f(x)=\frac{1}{x}$ yalijitokeza juu ya axes zote mbili, matokeo itakuwa grafu ya awali, kama inavyoonekana katika Kielelezo$\PageIndex{21}$.

Tunasema kwamba grafu hizi ni sawa na asili. Kazi yenye grafu ambayo ni sawa na asili inaitwa kazi isiyo ya kawaida.

Kumbuka: Kazi haiwezi hata wala isiyo ya kawaida ikiwa haionyeshi ulinganifu. Kwa mfano,$f(x)=2^x$ ni hata wala isiyo ya kawaida. Pia, kazi pekee ambayo ni sawa na isiyo ya kawaida ni kazi ya mara kwa mara$f(x)=0$.

Ufafanuzi: Hata na Kazi isiyo ya kawaida

Kazi inaitwa hata kazi ikiwa kwa kila pembejeo$x$

$f(x)=f(−x)$

Grafu ya kazi hata ni sawa kuhusu y-axis.

Kazi inaitwa kazi isiyo ya kawaida ikiwa kwa kila pembejeo$x$

$f(x)=−f(−x)$

Grafu ya kazi isiyo ya kawaida ni sawa na asili.

Jinsi ya...

Kutokana formula kwa ajili ya kazi, kuamua kama kazi ni hata, isiyo ya kawaida, au wala.

Kuamua kama kazi inatimiza$f(x)=f(−x)$. Kama ni hivyo, ni hata.
Kuamua kama kazi inatimiza$f(x)=−f(−x)$. Kama ni hivyo, ni isiyo ya kawaida.
Kama kazi haina kukidhi ama utawala, ni hata wala isiyo ya kawaida.

Mfano$\PageIndex{13}$: Determining whether a Function Is Even, Odd, or Neither

Je, kazi$f(x)=x^3+2x$ hata, isiyo ya kawaida, au wala?

Suluhisho

Bila kuangalia grafu, tunaweza kuamua kama kazi ni hata au isiyo ya kawaida kwa kutafuta formula kwa tafakari na kuamua kama wao kurudi sisi kazi ya awali. Hebu tuanze na utawala wa kazi hata.

\[f(−x)=(−x)^3+2(−x)=−x^3−2x \nonumber\]

Hii haina kurudi sisi kazi ya awali, hivyo kazi hii ni hata. Sasa tunaweza mtihani utawala kwa ajili ya kazi isiyo ya kawaida.

\[−f(−x)=−(−x^3−2x)=x^3+2x \nonumber\]

Kwa sababu$−f(−x)=f(x)$, hii ni kazi isiyo ya kawaida.

Uchambuzi

Fikiria grafu ya$f$ katika Kielelezo$\PageIndex{22}$. Angalia kwamba grafu ni sawa na asili. Kwa kila hatua$(x,y)$ kwenye grafu, hatua inayofanana pia$(−x,−y)$ iko kwenye grafu. Kwa mfano,$(1, 3)$ ni juu ya grafu ya$f$, na hatua sambamba pia$(−1,−3)$ ni kwenye grafu.

Zoezi$\PageIndex{8}$

Je, kazi$f(s)=s^4+3s^2+7$ hata, isiyo ya kawaida, au wala?

Jibu: hata

Kazi za kuchora Kutumia Stretches na Compressions

Kuongeza mara kwa mara kwa pembejeo au matokeo ya kazi ilibadilisha nafasi ya grafu kuhusiana na axes, lakini haikuathiri sura ya grafu. Sasa tunachunguza madhara ya kuzidisha pembejeo au matokeo kwa kiasi fulani.

Tunaweza kubadilisha ndani (maadili pembejeo) ya kazi au tunaweza kubadilisha nje (maadili pato) ya kazi. Kila mabadiliko ina athari maalum ambayo inaweza kuonekana graphically.

Kuweka wima na Compressions

Tunapozidisha kazi kwa mara kwa mara nzuri, tunapata kazi ambayo grafu imetambulishwa au imesisitizwa kwa wima kuhusiana na grafu ya kazi ya awali. Ikiwa mara kwa mara ni kubwa kuliko 1, tunapata kunyoosha wima; ikiwa mara kwa mara ni kati ya 0 na 1, tunapata compression wima. Kielelezo$\PageIndex{23}$ kinaonyesha kazi inayoongezeka kwa sababu za mara kwa mara 2 na 0.5 na kusababisha kunyoosha wima na ukandamizaji.

Grafu ya kazi inayoonyesha kunyoosha wima na ukandamizaji. — Kielelezo$\PageIndex{23}$: Kuweka wima na ukandamizaji

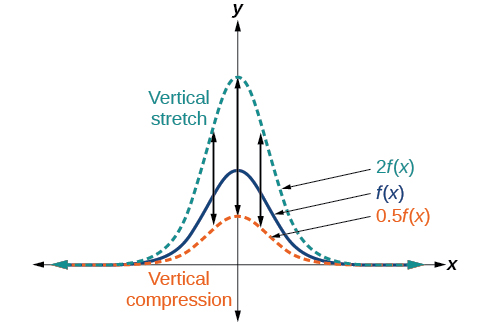
Ufafanuzi: Kuweka wima na Compressions

Kutokana na kazi$f(x)$, kazi mpya$g(x)=af(x)$, ambapo$a$ ni mara kwa mara, ni kunyoosha wima au compression wima ya kazi$f(x)$.

Ikiwa$a>1$, basi grafu itatambulishwa.
Ikiwa$0<a<1$, basi grafu itasisitizwa.
Ikiwa$a<0$, basi kutakuwa na mchanganyiko wa kunyoosha wima au ukandamizaji na kutafakari wima.

Jinsi ya...

Kutokana na kazi, grafu kunyoosha wima.

Tambua thamani ya$a$.
Panua maadili yote ya aina$a$
Kama$a>1$, grafu ni aliweka kwa sababu ya$a$.
Ikiwa$0<a<1$, grafu imesisitizwa na sababu ya$a$.
Ikiwa$a<0$, grafu ni ama kunyoosha au imesisitizwa na pia inaonekana kuhusu x-axis.

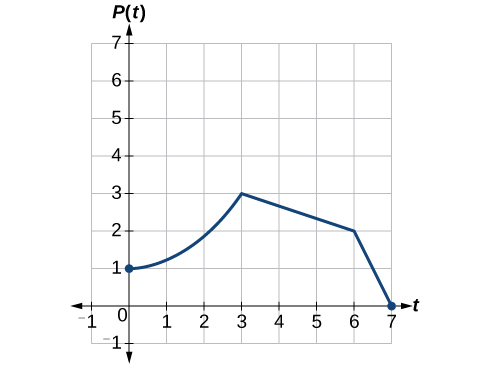
Mfano 1.5.14: Kuweka Kunyoosha kwa Wima

$P(t)$Mifano ya kazi idadi ya nzizi za matunda. Grafu inavyoonyeshwa kwenye Kielelezo$\PageIndex{24}$.

Kielelezo$\PageIndex{24}$: Grafu ili kuwakilisha ukuaji wa idadi ya nzizi za matunda.

Mwanasayansi analinganisha idadi hii na idadi ya watu$Q$ wengine, ambao ukuaji wake unafuata mfano huo, lakini ni mara mbili kubwa. Mchoro grafu ya idadi hii ya watu.

Suluhisho

Kwa sababu idadi ya watu daima ni mara mbili kubwa, maadili ya idadi ya watu wapya ya pato daima mara mbili ya awali ya kazi ya maadili ya pato. Graphically, hii inavyoonekana katika Kielelezo$\PageIndex{25}$.

Kama sisi kuchagua pointi nne kumbukumbu,$(0, 1)$,$(3, 3)$,$(6, 2)$ na$(7, 0)$ sisi kuzidisha yote ya matokeo kwa 2.

Yafuatayo inaonyesha ambapo pointi mpya za grafu mpya zitapatikana.

\[(0, 1)\rightarrow(0, 2)\]

\[(3, 3)\rightarrow(3, 6)\]

\[(6, 2)\rightarrow(6, 4)\]

\[(7, 0)\rightarrow(7, 0)\]

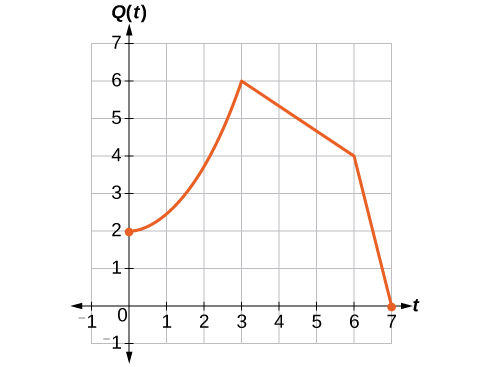
Kielelezo$\PageIndex{25}$: Grafu ya kazi ya idadi ya watu mara mbili.

Kwa mfano, uhusiano umeandikwa kama

\[Q(t)=2P(t) \nonumber\]

Hii ina maana kwamba kwa pembejeo yoyote$t$, thamani ya kazi$Q$ ni mara mbili thamani ya kazi$P$. Angalia kwamba athari kwenye grafu ni kunyoosha wima ya grafu, ambapo kila hatua huongeza umbali wake kutoka kwa mhimili usio na usawa. maadili pembejeo$t$, kukaa sawa wakati maadili pato ni mara mbili kubwa kama kabla.

Jinsi ya...

Kutokana na kazi ya tabular na kudhani kuwa mabadiliko ni kunyoosha wima au compression, kujenga meza kwa compression wima.

Kuamua thamani ya$a$.
Panua maadili yote ya pato na$a$.

Mfano$\PageIndex{15}$: Finding a Vertical Compression of a Tabular Function

Kazi$f$ inapewa kama Jedwali$\PageIndex{12}$. Unda meza kwa kazi$g(x)=\frac{1}{2}f(x)$.

Jedwali$\PageIndex{12}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Suluhisho

formula$g(x)=\frac{1}{2}f(x)$ inatuambia kwamba maadili ya pato ya$g$ ni nusu ya maadili ya pato ya$f$ na pembejeo sawa. Kwa mfano, tunajua hilo$f(4)=3$. Kisha

\[g(4)=\frac{1}{2}f(4)=\frac{1}{2}(3)=\frac{3}{2} \nonumber\]

Tunafanya hivyo kwa maadili mengine ya kuzalisha Jedwali$\PageIndex{13}$.

Jedwali$\PageIndex{13}$
$x$	2	4	6	8
$g(x)$	$\dfrac{1}{2}$	$\dfrac{3}{2}$	$\dfrac{7}{2}$	$\dfrac{11}{2}$

Uchambuzi

Matokeo yake ni kwamba kazi$g(x)$ imesisitizwa kwa wima na$\frac{1}{2}$. Kila thamani ya pato imegawanywa kwa nusu, hivyo grafu ni nusu ya urefu wa awali.

Zoezi$\PageIndex{9}$

Kazi$f$ inapewa kama Jedwali$\PageIndex{14}$. Unda meza kwa kazi$g(x)=\frac{3}{4}f(x)$.

Jedwali$\PageIndex{14}$
$x$	2	4	6	8
$f(x)$	12	16	20	0

Jibu

Jedwali$\PageIndex{15}$
$x$	2	4	6	8
$g(x)$	9	12	15	0

Mfano$\PageIndex{16}$: Recognizing a Vertical Stretch

Grafu katika Kielelezo$\PageIndex{26}$ ni mabadiliko ya kazi ya toolkit$f(x)=x^3$. Kuhusiana kazi hii mpya$g(x)$ kwa$f(x)$, na kisha kupata formula kwa$g(x)$.

[Grafu ya mabadiliko ya <span tafsiri = — Kielelezo$\PageIndex{26}$: Grafu ya mabadiliko ya$f(x)=x^3$

Unapojaribu kuamua kunyoosha wima au kuhama, ni muhimu kuangalia uhakika kwenye grafu ambayo ni wazi. Katika grafu hii, inaonekana kwamba$g(2)=2$. Pamoja na kazi ya msingi ya ujazo kwa pembejeo sawa,$f(2)=2^3=8$. Kulingana na kwamba, inaonekana kwamba matokeo ya$g$ ni matokeo$\frac{1}{4}$ ya kazi$f$ kwa sababu$g(2)=\frac{1}{4}f(2)$. Kutoka hili tunaweza kuhitimisha kwa usalama kwamba$g(x)=\frac{1}{4}f(x)$.

Tunaweza kuandika formula$g$ kwa kutumia ufafanuzi wa kazi$f$.

\[g(x)=\frac{1}{4} f(x)=\frac{1}{4}x^3.\]

Zoezi$\PageIndex{1}$

Andika formula kwa ajili ya kazi kwamba sisi kupata wakati sisi kunyoosha utambulisho toolkit kazi kwa sababu ya 3, na kisha kuhama chini kwa vitengo 2.

Jibu: $g(x)=3x-2$

Kuweka kwa usawa na Compressions

Sasa tunazingatia mabadiliko ndani ya kazi. Tunapozidisha pembejeo ya kazi kwa mara kwa mara nzuri, tunapata kazi ambayo grafu imetambulishwa au imesisitizwa kwa usawa kuhusiana na grafu ya kazi ya awali. Ikiwa mara kwa mara ni kati ya 0 na 1, tunapata kunyoosha usawa; ikiwa mara kwa mara ni kubwa kuliko 1, tunapata compression usawa wa kazi.

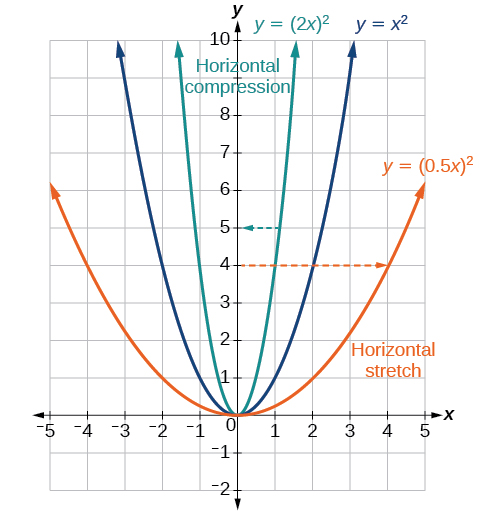
Grafu ya kunyoosha wima na compression ya x ^ 2. — Kielelezo$\PageIndex{27}$: Grafu ya kunyoosha wima na compression ya$x^2$.

Kutokana na kazi$y=f(x)$, fomu$y=f(bx)$ husababisha kunyoosha usawa au ukandamizaji. Fikiria kazi$y=x^2$. Angalia Kielelezo$\PageIndex{27}$. Grafu ya$y=(0.5x)^2$ ni kunyoosha usawa wa grafu ya kazi$y=x^2$ kwa sababu ya 2. Grafu ya$y=(2x)^2$ ni compression usawa wa grafu ya kazi$y=x^2$ kwa sababu ya 2.

Ufafanuzi: Kuweka kwa usawa na Compressions

Kutokana na kazi$f(x)$, kazi mpya$g(x)=f(bx)$, ambapo$b$ ni mara kwa mara, ni kunyoosha usawa au compression usawa wa kazi$f(x)$.

Ikiwa$b>1$, basi grafu itasisitizwa na$\frac{1}{b}$.
Ikiwa$0<b<1$, basi grafu itatambulishwa na$\frac{1}{b}$.
Ikiwa$b<0$, basi kutakuwa na mchanganyiko wa kunyoosha usawa au ukandamizaji na kutafakari kwa usawa.

Jinsi ya...

Kutokana na maelezo ya kazi, mchoro compression usawa au kunyoosha.

Andika formula ili kuwakilisha kazi.
Weka$g(x)=f(bx)$ wapi$b>1$ kwa compression au$0<b<1$ kwa kunyoosha.

Mfano$\PageIndex{17}$: Graphing a Horizontal Compression

Tuseme mwanasayansi ni kulinganisha idadi ya nzi matunda na idadi ya watu kwamba inaendelea kwa njia ya maisha yake mara mbili kwa haraka kama idadi ya awali. Kwa maneno mengine, idadi hii mpya$R$, itakuwa maendeleo katika 1 saa kiasi sawa na idadi ya awali haina katika 2 masaa, na katika 2 masaa, itakuwa maendeleo kama vile idadi ya awali haina katika 4 masaa. Mchoro grafu ya idadi hii ya watu.

Suluhisho

Symbolically, tunaweza kuandika

$\begin{align} R(1)&=P(2), \\ R(2)&=P(4), &\text{and in general,} \\ R(t)&=P(2t).\end{align}$

Angalia Kielelezo$\PageIndex{28}$ kwa kulinganisha graphical ya idadi ya awali na idadi ya watu USITUMIE.

Grafu mbili za upande kwa upande. Grafu ya kwanza ina kazi kwa idadi ya awali ambao uwanja wao ni [0,7] na upeo ni [0,3]. Thamani ya juu hutokea saa (3,3). Grafu ya pili ina umbo sawa na la kwanza isipokuwa ni nusu pana. Ni grafu ya idadi ya watu waliobadilishwa, ikiwa na kikoa cha [0, 3.5] na mbalimbali ya [0,3]. Upeo hutokea saa (1.5, 3). — Kielelezo$\PageIndex{28}$: (a) Original idadi ya watu grafu (b) Compressed idadi ya watu

Uchambuzi

Kumbuka kuwa athari kwenye grafu ni compression usawa ambapo maadili yote ya pembejeo ni nusu ya umbali wao wa awali kutoka mhimili wima.

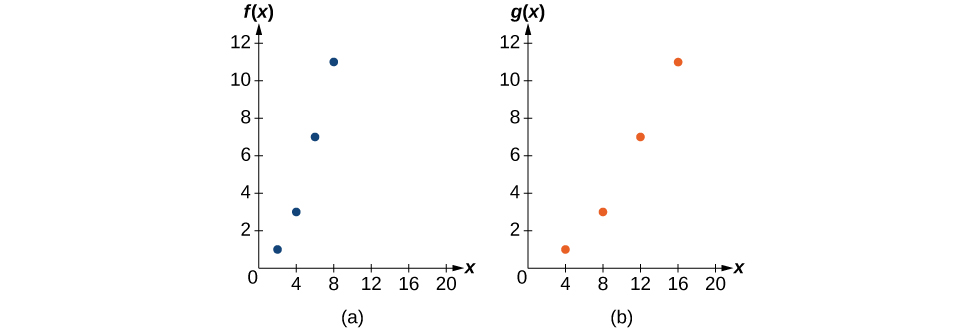
Mfano$\PageIndex{18}$: Finding a Horizontal Stretch for a Tabular Function

Kazi$f(x)$ inapewa kama Jedwali$\PageIndex{16}$. Unda meza kwa kazi$g(x)=f(\frac{1}{2}x)$.

Jedwali$\PageIndex{16}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

formula$g(x)=f(\frac{1}{2}x)$ inatuambia kwamba maadili pato kwa$g$ ni sawa na maadili pato kwa ajili ya kazi$f$ katika pembejeo nusu ukubwa. Kumbuka kwamba hatuna taarifa za kutosha kuamua$g(2)$ kwa sababu$g(2)=f(\frac{1}{2}⋅2)=f(1)$, na hatuna thamani ya$f(1)$ katika meza yetu. Maadili yetu ya pembejeo kwa$g$ itahitaji kuwa mara mbili kubwa ili kupata pembejeo kwa$f$ kuwa tunaweza kutathmini. Kwa mfano, tunaweza kuamua$g(4)$.

\[g(4)=f(\dfrac{1}{2}⋅4)=f(2)=1\]

Tunafanya hivyo kwa maadili mengine ya kuzalisha Jedwali$\PageIndex{17}$.

Jedwali$\PageIndex{17}$
$x$	4	8	12	16
$g(x)$	1	3	7	11

Kielelezo$\PageIndex{29}$ kinaonyesha grafu ya seti hizi mbili za pointi.

Kielelezo$\PageIndex{29}$: Grafu ya meza ya awali.

Uchambuzi

Kwa sababu kila thamani ya pembejeo imekuwa mara mbili, matokeo yake ni kwamba kazi$g(x)$ imekuwa aliweka sambamba na sababu ya 2.

Mfano$\PageIndex{19}$: Recognizing a Horizontal Compression on a Graph

Kuhusiana na kazi$g(x)$$f(x)$ katika Kielelezo$\PageIndex{30}$.

Suluhisho

Grafu ya$g(x)$ inaonekana kama grafu ya kusisitizwa$f(x)$ kwa usawa. Kwa sababu$f(x)$ mwisho katika (6,4) na$g(x)$ kuishia katika (2,4), tunaweza kuona kwamba x-maadili kuwa USITUMIE na$\frac{1}{3}$, kwa sababu$6(\frac{1}{3})=2$. Tunaweza pia taarifa kwamba$g(2)=f(6)$ na$g(1)=f(3)$. Kwa njia yoyote, tunaweza kuelezea uhusiano huu kama$g(x)=f(3x)$. Hii ni compression usawa na$\frac{1}{3}$.

Uchambuzi

Angalia kwamba mgawo unaohitajika kwa kunyoosha usawa au ukandamizaji ni usawa wa kunyoosha au ukandamizaji. Hivyo ili kunyoosha grafu kwa usawa na sababu ya kiwango cha 4, tunahitaji$\frac{1}{4}$ mgawo wa kazi yetu:$f(\frac{1}{4}x)$. Hii ina maana kwamba maadili ya pembejeo yanapaswa kuwa mara nne kubwa ili kuzalisha matokeo sawa, yanahitaji pembejeo kuwa kubwa, na kusababisha kuenea kwa usawa.

Zoezi$\PageIndex{11}$

Andika formula kwa ajili ya kazi ya mizizi ya mraba ya toolkit kwa usawa uliowekwa kwa sababu ya 3.

Jibu: $g(x)=f(\frac{1}{3}x)$, hivyo kutumia kazi ya mizizi ya mraba tunayopata$g(x)=\sqrt{\frac{1}{3}x}$

Kufanya Mlolongo wa Mabadiliko

Wakati wa kuchanganya mabadiliko, ni muhimu kuzingatia utaratibu wa mabadiliko. Kwa mfano, wima kuhama kwa 3 na kisha wima kunyoosha na 2 haina kujenga grafu sawa na wima kunyoosha kwa 2 na kisha wima kuhama kwa 3, kwa sababu wakati sisi kuhama kwanza, wote kazi ya awali na mabadiliko kupata aliweka, wakati tu kazi ya awali anapata aliweka wakati sisi kunyoosha kwanza.

Tunapoona maneno kama vile$2f(x)+3$, ni mabadiliko gani tunapaswa kuanza na? Jibu hapa linafuata vizuri kutoka kwa utaratibu wa shughuli. Kutokana na thamani ya pato la$f(x)$, sisi kwanza kuzidisha kwa 2, na kusababisha kunyoosha wima, na kisha kuongeza 3, na kusababisha mabadiliko wima. Kwa maneno mengine, kuzidisha kabla ya kuongeza.

Mabadiliko ya usawa ni trickier kidogo kufikiri juu. Tunapoandika$g(x)=f(2x+3)$, kwa mfano, tunapaswa kufikiri juu ya jinsi pembejeo za kazi$g$ zinahusiana na pembejeo kwa kazi$f$. Tuseme tunajua$f(7)=12$. Nini pembejeo kwa$g$ ingekuwa kuzalisha kwamba pato? Kwa maneno mengine, nini thamani ya$x$ itaruhusu$g(x)=f(2x+3)=12?$ Tunataka haja$2x+3=7$. Ili kutatua$x$, tunataka kwanza kuondoa 3, na kusababisha mabadiliko ya usawa, na kisha ugawanye na 2, na kusababisha compression usawa.

Fomu hii inaishia kuwa vigumu sana kufanya kazi na, kwa sababu kwa kawaida ni rahisi sana kunyoosha grafu kabla ya kuhama. Tunaweza kufanya kazi karibu na hili kwa factoring ndani ya kazi.

\[f(bx+p)=f(b(x+\frac{p}{b})) \nonumber\]

Hebu tufanye kazi kupitia mfano.

\[f(x)=(2x+4)^2 \nonumber\]

Tunaweza sababu nje 2.

\[f(x)=(2(x+2))^2 \nonumber\]

Sasa tunaweza kuona wazi mabadiliko ya usawa kwa vitengo 2 vya kushoto na compression usawa. Kuzingatia kwa njia hii inatuwezesha kunyoosha usawa kwanza na kisha kuhama kwa usawa.

Kuchanganya Mabadiliko

Wakati wa kuchanganya mabadiliko ya wima yaliyoandikwa kwa fomu$af(x)+k$, kwanza kunyoosha kwa wima$a$ na kisha kugeuka kwa wima$k$.
Wakati wa kuchanganya mabadiliko ya usawa yaliyoandikwa kwa fomu$f(bx+h)$, kwanza kuhama kwa usawa$h$ na kisha kunyoosha kwa usawa$\frac{1}{b}$.
Wakati wa kuchanganya mabadiliko ya usawa yaliyoandikwa kwa fomu$f(b(x+h))$, kwanza kunyoosha kwa usawa$\frac{1}{b}$ na kisha kuhama kwa usawa$h$.
Mabadiliko ya usawa na wima yanajitegemea. Haijalishi kama mabadiliko ya usawa au wima yanafanywa kwanza.

Mfano$\PageIndex{20}$: Finding a Triple Transformation of a Tabular Function

Kutokana na Jedwali$\PageIndex{18}$ kwa ajili ya kazi$f(x)$, kujenga meza ya maadili kwa ajili ya kazi$g(x)=2f(3x)+1$.

Jedwali$\PageIndex{18}$
$x$	6	12	18	24
$f(x)$	10	14	15	17

Suluhisho

Kuna hatua tatu za mabadiliko haya, na tutafanya kazi kutoka ndani nje. Kuanzia na mabadiliko ya usawa,$f(3x)$ ni compression usawa na$\frac{1}{3}$, ambayo ina maana sisi kuzidisha kila$x$ -thamani na$\frac{1}{3}$ .Angalia Jedwali$\PageIndex{19}$.

Jedwali$\PageIndex{19}$
$x$	2	4	6	8
$f(3x)$	10	14	15	17

Kuangalia sasa kwa mabadiliko ya wima, tunaanza na kunyoosha wima, ambayo itazidisha maadili ya pato kwa 2. Tunatumia hii kwa mabadiliko ya awali. Angalia Jedwali$\PageIndex{20}$.

Jedwali$\PageIndex{20}$
$x$	2	4	6	8
$2f(3x)$	20	28	30	34

Hatimaye, tunaweza kutumia mabadiliko ya wima, ambayo itaongeza 1 kwa maadili yote ya pato. Angalia Jedwali$\PageIndex{21}$.

Jedwali$\PageIndex{21}$
$x$	2	4	6	8
$g(x)=2f(3x)+1+1$	21	29	31	35

Mfano$\PageIndex{21}$: Finding a Triple Transformation of a Graph

Matumizi grafu ya$f(x)$ katika Kielelezo$\PageIndex{31}$ mchoro grafu ya$k(x)=f\Big(\frac{1}{2}x+1\Big)−3$.

Kielelezo$\PageIndex{31}$: Grafu ya mduara wa nusu.

Ili kurahisisha, hebu tuanze kwa kuzingatia ndani ya kazi.

\[f\Big(\dfrac{1}{2}x+1\Big)−3=f\Big(\dfrac{1}{2}(x+2)\Big)−3\]

Kwa kuzingatia ndani, tunaweza kwanza kunyoosha kwa usawa na 2, kama ilivyoonyeshwa na ndani ya kazi.$\frac{1}{2}$ Kumbuka kwamba mara mbili ukubwa wa 0 bado ni 0, hivyo hatua$(0,2)$ inabakia$(0,2)$ wakati hatua$(2,0)$ itakuwa kunyoosha kwa$(4,0)$. Angalia Kielelezo$\PageIndex{32}$.

alt — Kielelezo$\PageIndex{32}$: Grafu ya mduara wa nusu ya kunyoosha wima.

Kisha, sisi kuhama kwa usawa kushoto na vitengo 2, kama ilivyoonyeshwa na$x+2$. Angalia Kielelezo$\PageIndex{33}$.

alt — Kielelezo$\PageIndex{33}$: Grafu ya kunyoosha wima na kutafsiriwa nusu ya mduara.

Mwisho, sisi hubadilika chini na 3 ili kukamilisha mchoro wetu, kama ilivyoonyeshwa na 1-3 nje ya kazi. Angalia Kielelezo$\PageIndex{34}$.

alt — Kielelezo$\PageIndex{34}$: Grafu ya kunyoosha wima na kutafsiriwa nusu ya mduara.

Mlinganyo muhimu

Kubadilisha wima$g(x)=f(x)+k$ (hadi$k>0$)
Kuhama kwa usawa$g(x)=f(x−h)$ (kulia) kwa$h>0$
Reflection wima$g(x)=−f(x)$
Kutafakari kwa usawa$g(x)=f(−x)$
Kunyoosha wima$g(x)=af(x)$ (a>0)
Ukandamizaji wa wima$g(x)=af(x)$ (0<a<1)
Kunyoosha kwa usawa$g(x)=f(bx)(0<b<1)$
Ukandamizaji wa usawa$g(x)=f(bx)$ (b>1)

Dhana muhimu

Kazi inaweza kubadilishwa kwa wima kwa kuongeza mara kwa mara kwa pato.
Kazi inaweza kubadilishwa kwa usawa kwa kuongeza mara kwa mara kwa pembejeo.
Kuhusiana na mabadiliko ya mazingira ya tatizo hufanya iwezekanavyo kulinganisha na kutafsiri mabadiliko ya wima na ya usawa.
Mabadiliko ya wima na ya usawa mara nyingi huunganishwa.
Reflection wima inaonyesha grafu kuhusu x-axis. Grafu inaweza kuonekana kwa wima kwa kuzidisha pato kwa -1.
Kutafakari kwa usawa kunaonyesha grafu kuhusu mhimili wa y. Grafu inaweza kuonekana kwa usawa kwa kuzidisha pembejeo kwa -1.
Grafu inaweza kuonekana wote kwa wima na kwa usawa. Utaratibu ambao tafakari hutumiwa hauathiri grafu ya mwisho.
Kazi iliyotolewa katika fomu ya tabular inaweza pia kuonekana kwa kuzidisha maadili katika safu za pembejeo na pato au nguzo ipasavyo.
Kazi iliyotolewa kama equation inaweza kuonekana kwa kutumia mabadiliko moja kwa wakati.
Hata kazi zinalingana kuhusu mhimili wa y, wakati kazi isiyo ya kawaida ni sawa na asili.
Hata kazi zinakidhi hali hiyo$f(x)=f(−x)$.
Kazi isiyo ya kawaida kukidhi hali hiyo$f(x)=−f(−x)$.
Kazi inaweza kuwa isiyo ya kawaida, hata, au wala.
Kazi inaweza kusisitizwa au kunyoosha kwa wima kwa kuzidisha pato kwa mara kwa mara.
Kazi inaweza kusisitizwa au kunyoosha kwa usawa kwa kuzidisha pembejeo kwa mara kwa mara.
Utaratibu ambao mabadiliko tofauti hutumiwa huathiri kazi ya mwisho. Mabadiliko yote ya wima na ya usawa yanapaswa kutumika kwa utaratibu uliotolewa. Hata hivyo, mabadiliko ya wima yanaweza kuunganishwa na mabadiliko ya usawa kwa utaratibu wowote.

faharasa

hata kazi

kazi ambayo grafu haibadilishwa na kutafakari kwa usawa$f(x)=f(−x)$,, na inalinganishwa kuhusu mhimili wa y

compression
usawa mabadiliko ambayo compresses grafu ya kazi kwa usawa, kwa kuzidisha pembejeo kwa mara kwa mara b> 1

kutafakari
kwa usawa mabadiliko ambayo yanaonyesha grafu ya kazi kwenye mhimili wa y kwa kuzidisha pembejeo kwa -1

mabadiliko
ya usawa mabadiliko ambayo hubadilisha grafu ya kazi kushoto au kulia kwa kuongeza mara kwa mara chanya au hasi kwa pembejeo

unyoosha
usawa mabadiliko ambayo huweka grafu ya kazi kwa usawa kwa kuzidisha pembejeo kwa mara 0<b<1

kazi isiyo
ya kawaida - kazi ambayo grafu haibadilishwa na kutafakari kwa pamoja$f(x)=−f(−x)$, usawa na wima, na ni sawa na asili

compression
wima mabadiliko ya kazi ambayo compresses grafu ya kazi wima kwa kuzidisha pato kwa mara 0<a <1

kutafakari
wima mabadiliko ambayo yanaonyesha grafu ya kazi kwenye mhimili wa x-kwa kuzidisha pato kwa -1

mabadiliko
ya wima mabadiliko ambayo hubadilisha grafu ya kazi juu au chini kwa kuongeza mara kwa mara chanya au hasi kwa pato

kunyoosha
wima mabadiliko ambayo huweka grafu ya kazi kwa wima kwa kuzidisha pato kwa mara kwa mara> 1

\(x\)	2	4	6	8
\(f(x)\)	1	3	7	11
\(g(x)\)	-2	0	4	8

\(x\)	5	7	9	11
\(x-3\)	2	4	6	8
\(f(x)\)	1	3	7	11
\(g(x)\)	1	3	7	11

\(x\)	2	4	6	8
\(g(x)\)	\(\dfrac{1}{2}\)	\(\dfrac{3}{2}\)	\(\dfrac{7}{2}\)	\(\dfrac{11}{2}\)

Jedwali\(\PageIndex{8}\)
\(x\)	-2	-4	-6	-8
\(h(x)\)	1	3	7	11

Jedwali\(\PageIndex{11}\)
\(x\)	-2	0	2	-4
\(h(x)\)	15	10	5	20

Jedwali\(\PageIndex{19}\)
\(x\)	2	4	6	8
\(f(3x)\)	10	14	15	17

Jedwali\(\PageIndex{20}\)
\(x\)	2	4	6	8
\(2f(3x)\)	20	28	30	34