6.2: Usambazaji wa kawaida wa kawaida

Z-alama

Usambazaji wa kawaida wa kawaida ni usambazaji wa kawaida wa maadili sanifu inayoitwa z-scores. Alama ya z-inapimwa katika vitengo vya kupotoka kwa kawaida.

Ufafanuzi: Z-Score

Kama\(X\) ni kawaida kusambazwa random variable na\(X \sim N(\mu, \sigma)\), kisha z -score ni:

\[z = \dfrac{x - \mu}{\sigma} \label{zscore}\]

z -score inakuambia jinsi wengi kiwango deviations thamani\(x\) ni juu (na haki ya) au chini (upande wa kushoto wa) maana,\(\mu\). Maadili ya\(x\) kwamba ni kubwa kuliko maana na chanya\(z\) -alama, na maadili ya\(x\) kwamba ni ndogo kuliko maana na hasi\(z\) -alama. Ikiwa\(x\) ni sawa na maana, basi\(x\) ina\(z\) alama ya sifuri. Kwa mfano, ikiwa maana ya usambazaji wa kawaida ni tano na kupotoka kwa kiwango ni mbili, thamani 11 ni upungufu wa kiwango cha tatu juu (au haki ya) maana. Mahesabu ni kama ifuatavyo:

\[ \begin{align*} x &= \mu + (z)(\sigma) \\[5pt] &= 5 + (3)(2) = 11 \end{align*}\]

z -alama ni tatu.

Kwa kuwa maana ya usambazaji wa kawaida ni sifuri na kupotoka kwa kawaida ni moja, basi mabadiliko katika Equation\ ref {zscore} hutoa usambazaji\(Z \sim N(0, 1)\). Thamani\(x\) hutoka kwa usambazaji wa kawaida na kupotoka kwa maana\(\mu\) na kiwango\(\sigma\).

Alama ya z-inapimwa katika vitengo vya kupotoka kwa kawaida.

Mfano\(\PageIndex{1}\)

Tuseme\(X \sim N(5, 6)\). Hii inasema kwamba\(x\) ni kawaida kusambazwa random variable na maana\(\mu = 5\) na kiwango kupotoka\(\sigma = 6\). Tuseme\(x = 17\). Kisha (kupitia Ulinganisho\ ref {alama}):

\[z = \dfrac{x-\mu}{\sigma} = \dfrac{17-5}{6} = 2 \nonumber\]

Hii ina maana kwamba\(x = 17\) ni mbili kupotoka kiwango (2\(\sigma\)) juu au haki ya maana\(\mu = 5\). Kupotoka kwa kiwango ni\(\sigma = 6\).

Kumbuka kwamba:\(5 + (2)(6) = 17\) (mfano ni\(\mu + z \sigma = x\))

Sasa tuseme\(x = 1\). Kisha:

\[z = \dfrac{x-\mu}{\sigma} = \dfrac{1-5}{6} = -0.67 \nonumber\]

(mviringo kwa maeneo mawili ya decimal)

Hii ina maana kwamba\(x = 1\) ni\(0.67\) kiwango deviations (\(–0.67\sigma\)) chini au upande wa kushoto wa maana\(\mu = 5\). Kumbuka kwamba:\(5 + (–0.67)(6)\) ni takriban sawa na moja (Hii ina mfano\(\mu + (–0.67)\sigma = 1\))

Kuhitimisha, wakati\(z\)\(x\) ni chanya, ni juu au haki ya\(\mu\) na wakati\(z\) ni hasi,\(x\) ni upande wa kushoto au chini\(\mu\). Au, wakati\(z\) ni chanya,\(x\) ni kubwa kuliko\(\mu\), na wakati\(z\) ni hasi\(x\) ni chini ya\(\mu\).

Zoezi\(\PageIndex{1}\)

Ni nini\(z\) -alama ya\(x\), wakati\(x = 1\) na\(X \sim N(12, 3)\)?

Jibu

\(z = \dfrac{1-12}{3} \approx -3.67\)

Mfano\(\PageIndex{2}\)

Madaktari wengine wanaamini kwamba mtu anaweza kupoteza paundi tano, kwa wastani, kwa mwezi kwa kupunguza ulaji wake wa mafuta na kwa kutumia mara kwa mara. Tuseme kupoteza uzito kuna usambazaji wa kawaida. Hebu kiasi\(X =\) cha uzito kilichopotea (kwa paundi) na mtu kwa mwezi. Tumia kupotoka kwa kiwango cha paundi mbili. \(X \sim N(5, 2)\). Jaza vifungo.

1. Tuseme mtu alipoteza paundi kumi kwa mwezi. \(z\)-alama wakati\(x = 10\) paundi ni\(x = 2.5\) (kuthibitisha). Hii\(z\) -alama inakuambia kuwa\(x = 10\) ni ________ kiwango kupotoka kwa ________ (kulia au kushoto) ya maana _____ (Nini maana?).
2. Tuseme mtu alipata paundi tatu (kupoteza uzito hasi). Kisha\(z =\) __________. Hii\(z\) -alama inakuambia kuwa\(x = -3\) ni ________ kiwango kupotoka kwa __________ (kulia au kushoto) ya maana.

Majibu

a. hii\(z\) -alama atakwambia kwamba\(x = 10\) ni 2.5 kiwango kupotoka na haki ya maana tano.

b. tuseme vigezo random\(X\) na\(Y\) kuwa na yafuatayo mgawanyo kawaida:\(X \sim N(5, 6)\) na\(Y \sim N(2, 1)\). Ikiwa\(x = 17\), basi\(z = 2\). (Hii ilionyeshwa hapo awali.) Ikiwa\(y = 4\), ni nini\(z\)?

\[z = \dfrac{y-\mu}{\sigma} = \dfrac{4-2}{1} = 2 \nonumber\]

wapi\(\mu = 2\) na\(\sigma = 1\).

\(z\)-alama kwa\(y = 4\) ni\(z = 2\). Hii ina maana kwamba nne ni upungufu wa\(z = 2\) kawaida kwa haki ya maana. Kwa hiyo,\(x = 17\) na\(y = 4\) wawili wawili (wao wenyewe) kupotoka kiwango na haki ya njia zao.

z -score inaruhusu sisi kulinganisha data kwamba ni kuongezwa tofauti. Ili kuelewa dhana, tuseme\(X \sim N(5, 6)\) inawakilisha faida ya uzito kwa kundi moja la watu ambao wanajaribu kupata uzito katika kipindi cha wiki sita na\(Y \sim N(2, 1)\) kupima uzito sawa kwa kundi la pili la watu. Faida mbaya ya uzito itakuwa kupoteza uzito. Kwa kuwa\(x = 17\) na kila aina mbili\(y = 4\) za upungufu wa kawaida kwa haki ya njia zao, zinawakilisha sawa, faida ya uzito sawa na njia zao.

Zoezi\(\PageIndex{2}\)

Jaza vifungo.

Jerome wastani 16 anasema mchezo na kupotoka kiwango cha pointi nne. \(X \sim N(16, 4)\). Tuseme Jerome alama pointi kumi katika mchezo. The\(z\) -score wakati\(x = 10\) ni\(-1.5\). Alama hii inakuambia kuwa\(x = 10\) ni _____ kiwango kupotoka kwa ______ (kulia au kushoto) ya maana______ (Nini maana?).

Jibu

1.5, kushoto, 16

Utawala wa kimapenzi

Ikiwa\(X\) ni variable ya random na ina usambazaji wa kawaida na kupotoka kwa maana\(\mu\) na kiwango\(\sigma\), basi Utawala wa Empirical unasema yafuatayo:

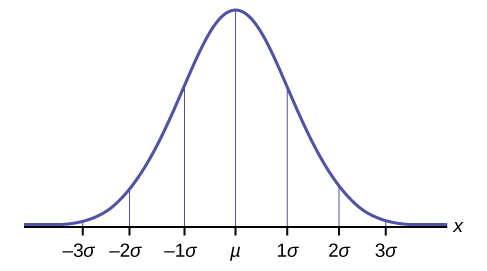
• Kuhusu 68% ya\(x\) maadili hulala kati ya -1\(\sigma\) na +1\(\sigma\) ya maana\(\mu\) (ndani ya kupotoka kwa kiwango kimoja cha maana).
• Kuhusu 95% ya\(x\) maadili hulala kati ya -2\(\sigma\) na +2\(\sigma\) ya maana\(\mu\) (ndani ya upungufu wa kawaida wa maana).
• Kuhusu 99.7% ya\(x\) maadili hulala kati ya -3\(\sigma\) na +3\(\sigma\) ya maana\(\mu\) (ndani ya upungufu wa kiwango cha wastani wa maana). Angalia kwamba karibu\(x\) maadili yote yanalala ndani ya upungufu wa kiwango cha tatu cha maana.
• The\(z\) -alama kwa +1\(\sigma\) na -1\(\sigma\) ni +1 na -1, kwa mtiririko huo.
• \(z\)Alama za +2\(\sigma\) na -2\(\sigma\) ni +2 na -2, kwa mtiririko huo.
• \(z\)Alama za +3\(\sigma\) na -3\(\sigma\) ni +3 na -3 kwa mtiririko huo.

Utawala wa upimaji pia unajulikana kama utawala wa 68-95-99.7.

Kielelezo\(\PageIndex{1}\)

Mfano\(\PageIndex{3}\)

Urefu wa wastani wa wanaume wenye umri wa miaka 15 hadi 18 kutoka Chile kutoka 2009 hadi 2010 ulikuwa 170 cm na kupotoka kwa kiwango cha 6.28 cm. Urefu wa kiume hujulikana kufuata usambazaji wa kawaida. Hebu urefu\(X =\) wa kiume mwenye umri wa miaka 15 hadi 18 kutoka Chile mwaka 2009 hadi 2010. Kisha\(X \sim N(170, 6.28)\).

1. Tuseme kiume mwenye umri wa miaka 15 hadi 18 kutoka Chile alikuwa na urefu wa sentimita 168 kuanzia mwaka 2009 hadi 2010. The\(z\) -alama wakati\(x = 168\) cm ni\(z =\) _______. Hii\(z\) -alama inakuambia kuwa\(x = 168\) ni ________ kiwango kupotoka kwa ________ (kulia au kushoto) ya maana _____ (Nini maana?).
2. Tuseme kwamba urefu wa kiume mwenye umri wa miaka 15 hadi 18 kutoka Chile kutoka 2009 hadi 2010 ina\(z\) alama ya\(z = 1.27\). Urefu wa kiume ni nini? The\(z\) -score (\(z = 1.27\)) inakuambia kuwa urefu wa kiume ni ________ upungufu wa kiwango kwa __________ (kulia au kushoto) ya maana.

Majibu

1. —0.32, 0.32, kushoto, 170
2. 177.98, 1.27, haki

Zoezi\(\PageIndex{3}\)

Tumia maelezo katika Mfano\(\PageIndex{3}\) ili kujibu maswali yafuatayo.

1. Tuseme kiume mwenye umri wa miaka 15 hadi 18 kutoka Chile alikuwa urefu wa sentimita 176 kutoka 2009 hadi 2010. The\(z\) -alama wakati\(x = 176\) cm ni\(z =\) _______. Hii\(z\) -alama inakuambia kwamba\(x = 176\) cm ni ________ kiwango kupotoka kwa ________ (kulia au kushoto) ya maana _____ (Nini maana?).
2. Tuseme kwamba urefu wa kiume mwenye umri wa miaka 15 hadi 18 kutoka Chile kutoka 2009 hadi 2010 ina\(z\) alama ya\(z = –2\). Urefu wa kiume ni nini? The\(z\) -score (\(z = –2\)) inakuambia kuwa urefu wa kiume ni ________ upungufu wa kiwango kwa __________ (kulia au kushoto) ya maana.

Jibu

Kutatua equation\(z = \dfrac{x-\mu}{\sigma}\) kwa\(z\). \(x = \mu+ (z)(\sigma)\)

\(z = \dfrac{176-170}{6.28}\), Hii z -score inakuambia kuwa\(x = 176\) cm ni 0.96 upungufu wa kawaida kwa haki ya wastani 170 cm.

Jibu

Kutatua equation\(z = \dfrac{x-\mu}{\sigma}\) kwa\(z\). \(x = \mu+ (z)(\sigma)\)

\(X = 157.44\)cm, The\(z\) -score (\(z = –2\)) inakuambia kuwa urefu wa kiume ni upungufu wa kiwango mbili upande wa kushoto wa maana.

Mfano\(\PageIndex{4}\)

Kutoka 1984 hadi 1985, urefu wa wastani wa wanaume wenye umri wa miaka 15 hadi 18 kutoka Chile ulikuwa 172.36 cm, na kupotoka kwa kiwango kilikuwa 6.34 cm. Hebu urefu\(Y =\) wa wanaume wenye umri wa miaka 15 hadi 18 kutoka 1984 hadi 1985. Kisha\(Y \sim N(172.36, 6.34)\).

Urefu wa wastani wa wanaume wenye umri wa miaka 15 hadi 18 kutoka Chile kutoka 2009 hadi 2010 ulikuwa 170 cm na kupotoka kwa kiwango cha 6.28 cm. Urefu wa kiume hujulikana kufuata usambazaji wa kawaida. Hebu urefu\(X =\) wa kiume mwenye umri wa miaka 15 hadi 18 kutoka Chile mwaka 2009 hadi 2010. Kisha\(X \sim N(170, 6.28)\).

Pata alama za z kwa\(x = 160.58\) cm na\(y = 162.85\) cm. Tafsiri kila\(z\) -alama. Unaweza kusema nini kuhusu\(x = 160.58\) cm na\(y = 162.85\) cm?

Jibu

• The\(z\) -score (Equation\ ref {alama}) kwa ajili ya\(x = 160.58\) ni\(z = –1.5\).
• \(z\)-alama kwa\(y = 162.85\) ni\(z = –1.5\).

Wote wawili\(x = 160.58\)\(y = 162.85\) na kupotosha idadi sawa ya upungufu wa kawaida kutoka kwa njia zao na katika mwelekeo huo.

Zoezi\(\PageIndex{4}\)

Mwaka 2012, wanafunzi 1,664,479 walichukua mtihani wa SAT. Usambazaji wa alama katika sehemu ya maneno ya SAT ulikuwa\(\mu = 496\) na maana na kupotoka kwa kawaida\(\sigma = 114\). Hebu\(X =\) SAT mtihani matusi sehemu alama katika 2012. Kisha\(X \sim N(496, 114)\).

Kupata\(z\) -alama kwa\(x_{1} = 325\) na\(x_{2} = 366.21\). Tafsiri kila\(z\) -alama. Unaweza kusema nini kuhusu\(x_{1} = 325\) na\(x_{2} = 366.21\)?

Jibu

z -alama (Equation\ ref {alama}) kwa ajili\(x_{1} = 325\) yetu\(z_{1} = –1.15\).

z -alama (Equation\ ref {alama}) kwa ajili\(x_{2} = 366.21\) yetu\(z_{2} = –1.14\).

Mwanafunzi 2 alifunga karibu na maana kuliko Mwanafunzi 1 na, kwa kuwa wote wawili walikuwa na\(z\) alama mbaya, Mwanafunzi 2 alikuwa na alama bora.

Mfano\(\PageIndex{5}\)

Tuseme x ina usambazaji wa kawaida na maana 50 na kiwango kupotoka 6.

• Kuhusu 68% ya maadili ya x hulala ndani ya kupotoka kwa kiwango kimoja cha maana. Kwa hiyo, takriban 68% ya maadili x hulala kati ya —1σ = (—1) (6) = —6 na 1σ = (1) (6) = 6 ya 50 ya wastani. Maadili 50 - 6 = 44 na 50 + 6 = 56 ni ndani ya kupotoka kwa kiwango kimoja kutoka kwa wastani 50. Alama za z ni -1 na +1 kwa 44 na 56, kwa mtiririko huo.
• Kuhusu 95% ya maadili ya x hulala ndani ya upungufu wa kawaida wa maana. Kwa hiyo, karibu 95% ya maadili x hulala kati ya —2σ = (—2) (6) = —12 na 2σ = (2) (6) = 12. Maadili 50 - 12 = 38 na 50 + 12 = 62 ni ndani ya upungufu wa kiwango mbili kutoka kwa wastani 50. Alama za z ni -2 na +2 kwa 38 na 62, kwa mtiririko huo.
• Kuhusu 99.7% ya maadili ya x hulala ndani ya upungufu wa kiwango cha tatu cha maana. Kwa hiyo, takriban 99.7% ya maadili x hulala kati ya —3σ = (—3) (6) = —18 na 3σ = (3) (6) = 18 kutoka kwa wastani 50. Maadili 50 - 18 = 32 na 50 + 18 = 68 ni ndani ya upungufu wa kiwango cha wastani wa 50. Alama za z ni -3 na +3 kwa 32 na 68, kwa mtiririko huo.

Zoezi\(\PageIndex{5}\)

Tuseme\(X\) ina usambazaji wa kawaida na maana 25 na kiwango kupotoka tano. Kati ya maadili gani ya\(x\) kufanya 68% ya maadili ya uongo?

Jibu

kati ya 20 na 30.

Mfano\(\PageIndex{6}\)

Kutoka 1984 hadi 1985, urefu wa wastani wa wanaume wenye umri wa miaka 15 hadi 18 kutoka Chile ulikuwa 172.36 cm, na kupotoka kwa kiwango kilikuwa 6.34 cm. Hebu urefu\(Y =\) wa wanaume wenye umri wa miaka 15 hadi 18 mwaka 1984 hadi 1985. Kisha\(Y \sim N(172.36, 6.34)\).

1. Kuhusu 68% ya\(y\) maadili ya uongo kati ya maadili mawili? Maadili haya ni ________________. \(z\)Alama -ni ________________, kwa mtiririko huo.
2. Kuhusu 95% ya\(y\) maadili ya uongo kati ya maadili mawili? Maadili haya ni ________________. \(z\)Alama -ni ________________ kwa mtiririko huo.
3. Kuhusu 99.7% ya\(y\) maadili ya uongo kati ya maadili mawili? Maadili haya ni ________________. \(z\)Alama -ni ________________, kwa mtiririko huo.

Jibu

1. Kuhusu 68% ya maadili ni kati ya 166.02 na 178.7. The\(z\) -alama ni —1 na 1.
2. Kuhusu 95% ya maadili ni kati ya 159.68 na 185.04. \(z\)Alama -ni —2 na 2.
3. Kuhusu 99.7% ya maadili ni kati ya 153.34 na 191.38. \(z\)Alama -ni -3 na 3.

Zoezi\(\PageIndex{6}\)

Alama kwenye mtihani wa kuingia chuo zina usambazaji wa kawaida wa wastani na maana,\(\mu = 52\) pointi na kupotoka kwa kiwango,\(\sigma = 11\) pointi.

1. Kuhusu 68% ya\(y\) maadili ya uongo kati ya maadili mawili? Maadili haya ni ________________. \(z\)Alama -ni ________________, kwa mtiririko huo.
2. Kuhusu 95% ya\(y\) maadili ya uongo kati ya maadili mawili? Maadili haya ni ________________. \(z\)Alama -ni ________________, kwa mtiririko huo.
3. Kuhusu 99.7% ya\(y\) maadili ya uongo kati ya maadili mawili? Maadili haya ni ________________. \(z\)Alama -ni ________________, kwa mtiririko huo.

Jibu

Kuhusu 68% ya maadili ya uongo kati ya maadili 41 na 63. The\(z\) -alama ni —1 na 1, kwa mtiririko huo.

Jibu b

Kuhusu 95% ya maadili hulala kati ya maadili 30 na 74. The\(z\) -alama ni —2 na 2, kwa mtiririko huo.

Jibu c

Kuhusu 99.7% ya maadili ya uongo kati ya maadili 19 na 85. \(z\)Alama -ni -3 na 3, kwa mtiririko huo.

Muhtasari

A\(z\) -score ni thamani sanifu. Usambazaji wake ni kiwango cha kawaida,\(Z \sim N(0,1)\). The mean of the \(z\)-scores is zero and the standard deviation is one. If \(y\) is the z -alama kwa thamani\(x\) from the normal distribution \(N(\mu, \sigma)\) then \(z\) tells you how many standard deviations \(x\) is above (greater than) or below (less than) \(\mu\).

Mapitio ya Mfumo

\(Z \sim N(0, 1)\)

\(z = a\)thamani sanifu (\(z\)-alama)

maana = 0; kiwango cha kupotoka = 1

Ili kupata asilimia\(K\) ^th ya\(X\) wakati\(z\) -alama inajulikana:

\(k = \mu + (z)\sigma\)

\(z\)-alama:\(z = \dfrac{x-\mu}{\sigma}\)

\(Z =\)variable random kwa z -alama

\(Z \sim N(0, 1)\)

faharasa

Usambazaji wa kawaida wa kawaida

kuendelea random variable (RV)\(X \sim N(0, 1)\); wakati\(X\) ifuatavyo kiwango usambazaji wa kawaida, mara nyingi hujulikana kama\ (Z\ sim N (0, 1)\.

\(z\)-alama

mabadiliko ya mstari wa fomu\(z = \dfrac{x-\mu}{\sigma}\); ikiwa mabadiliko haya yanatumika kwa usambazaji wowote\(X \sim N(\mu, \sigma\) wa kawaida, matokeo ni usambazaji wa kawaida wa kawaida\(Z \sim N(0,1)\). Kama mabadiliko haya inatumika kwa thamani yoyote maalum\(x\) ya RV na maana\(\mu\) na kiwango kupotoka\(\sigma\), matokeo inaitwa\(z\) -alama ya\(x\). The\(z\) -score inaruhusu sisi kulinganisha data kwamba ni kawaida kusambazwa lakini kuongezwa tofauti.

Marejeo

1. “Shinikizo la damu la Wanaume na Wanawake.” StatCruch, 2013. Inapatikana mtandaoni kwenye http://www.statcrunch.com/5.0/viewre...reportid=11960 (imefikia Mei 14, 2013).
2. “Matumizi ya Vyombo vya Epidemiological katika watu walioathirika na migogoro: Rasilimali za elimu zinazofungua kwa watunga sera: Hesabu ya alama za z. Shule ya London ya Usafi na Tropical Medicine, 2009. Inapatikana mtandaoni kwenye http://conflict.lshtm.ac.uk/page_125.htm (imefikia Mei 14, 2013).
3. “2012 Chuo amefungwa Wazee Jumla Group Profile Ripoti.” CollegeBoard, 2012. Inapatikana mtandaoni kwenye media.collegeboard.com/digita... Group-2012.pdf (imefikia Mei 14, 2013).
4. “Digest ya Elimu Takwimu: ACT alama wastani na kiwango kupotoka kwa ngono na mbio/ukabila na asilimia ya ACT mtihani takers, na kuchaguliwa safu Composite alama na maeneo iliyopangwa ya utafiti: Miaka kuchaguliwa, 1995 kwa 2009.” Kituo cha Taifa cha Elimu Takwimu. Inapatikana mtandaoni kwenye nces.ed.gov/programs/digest/d... s/dt09_147.asp (imefikia Mei 14, 2013).
5. Takwimu kutoka San Jose Mercury News.
6. Takwimu kutoka Dunia Almanac na Kitabu cha Mambo.
7. “Orodha ya viwanja kwa uwezo.” Wikipedia. Inapatikana mtandaoni kwenye en.wikipedia.org/wiki/list_o... ms_by_capacity (imefikia Mei 14, 2013).
8. Takwimu kutoka kwa Chama cha Taifa cha Mpira wa Inapatikana mtandaoni kwenye www.nba.com (imefikia Mei 14, 2013).