4.5: Usambazaji wa Kijiometri

Kuna sifa tatu kuu za jaribio la kijiometri.

1. Kuna majaribio moja au zaidi ya Bernoulli na kushindwa yote isipokuwa ya mwisho, ambayo ni mafanikio. Kwa maneno mengine, unaendelea kurudia kile unachofanya mpaka mafanikio ya kwanza. Kisha kuacha. Kwa mfano, wewe kutupa dart katika bullseye mpaka hit bullseye. Mara ya kwanza kugonga bullseye ni “mafanikio” hivyo uacha kutupa dart. Ni inaweza kuchukua majaribio sita mpaka hit bullseye. Unaweza kufikiria majaribio kama kushindwa, kushindwa, kushindwa, kushindwa, kushindwa, mafanikio, STOP.
2. Kwa nadharia, idadi ya majaribio inaweza kuendelea milele. Lazima iwe na angalau jaribio moja.
3. Uwezekano\(p\),, wa mafanikio na uwezekano,\(q\), wa kushindwa ni sawa kwa kila jaribio. \(p + q = 1\)na\(q = 1 − p\). Kwa mfano, uwezekano wa rolling tatu wakati kutupa moja ya haki kufa ni\(\dfrac{1}{6}\). Hii ni kweli bila kujali mara ngapi unaendelea kufa. Tuseme unataka kujua uwezekano wa kupata tatu za kwanza kwenye roll ya tano. Juu ya mistari moja hadi nne, huwezi kupata uso na tatu. Uwezekano wa kila moja ya mistari ni\(q = \dfrac{5}{6}\), uwezekano wa kushindwa. Uwezekano wa kupata tatu kwenye roll ya tano ni\(\left(\dfrac{5}{6}\right)\left(\dfrac{5}{6}\right)\left(\dfrac{5}{6}\right)\left(\dfrac{5}{6}\right)\left(\dfrac{1}{6}\right) = 0.0804\).

\(X =\)idadi ya majaribio ya kujitegemea mpaka mafanikio ya kwanza.

Kucheza mchezo wa nafasi uweze ama kushinda au kupoteza (hakuna uwezekano mwingine) mpaka kupoteza. Uwezekano wako wa kupoteza ni\(p = 0.57\). ni uwezekano kwamba inachukua mechi tano mpaka kupoteza nini? Hebu idadi\(X =\) ya michezo ya kucheza mpaka kupoteza (ni pamoja na mchezo kupoteza). Kisha\(X\) inachukua maadili 1, 2, 3,... (inaweza kwenda kwa muda usiojulikana). Swali la uwezekano ni\(P(x = 5)\).

Mfano\(\PageIndex{1}\)

Kucheza mchezo wa nafasi uweze ama kushinda au kupoteza (hakuna uwezekano mwingine) mpaka kupoteza. Uwezekano wako wa kupoteza ni\(p = 0.57\). ni uwezekano kwamba inachukua mechi tano mpaka kupoteza nini? Hebu idadi\(X =\) ya michezo ya kucheza mpaka kupoteza (ni pamoja na mchezo kupoteza). Kisha\(X\) inachukua maadili 1, 2, 3,... (inaweza kwenda kwa muda usiojulikana). Swali la uwezekano ni\(P(x = 5)\).

Zoezi\(\PageIndex{1}\)

Kutupa mishale katika bodi mpaka hit eneo la kituo cha. Uwezekano wako wa kupiga eneo la kituo ni\(p = 0.17\). Unataka kupata uwezekano kwamba inachukua nane throws mpaka hit kituo cha. Je! Maadili gani\(X\) huchukua?

Jibu

\(1, 2, 3, 4, \dotsc, n\). Inaweza kuendelea kwa muda usiojulikana.

Mfano\(\PageIndex{2}\)

Mhandisi wa usalama anahisi kuwa 35% ya ajali zote za viwanda katika mmea wake husababishwa na kushindwa kwa wafanyakazi kufuata maelekezo. Anaamua kutazama ripoti za ajali (zilizochaguliwa nasibu na kubadilishwa katika rundo baada ya kusoma) mpaka atakapopata moja inayoonyesha ajali iliyosababishwa na kushindwa kwa wafanyakazi kufuata maelekezo. Kwa wastani, ni ripoti ngapi ambazo mhandisi wa usalama atatarajia kuangalia mpaka atakapopata ripoti inayoonyesha ajali iliyosababishwa na kushindwa kwa mfanyakazi kufuata maelekezo? Ni uwezekano gani kwamba mhandisi wa usalama atalazimika kuchunguza angalau ripoti tatu mpaka atakapopata ripoti inayoonyesha ajali iliyosababishwa na kushindwa kwa mfanyakazi kufuata maelekezo?

Hebu\(X\) = idadi ya ajali ambayo mhandisi wa usalama anapaswa kuchunguza mpaka atakapopata ripoti inayoonyesha ajali iliyosababishwa na mfanyakazi kushindwa kufuata maelekezo. \(X\)inachukua maadili 1, 2, 3,... Swali la kwanza linakuuliza kupata thamani inayotarajiwa au maana. Swali la pili linakuuliza kupata\(P(x \geq 3)\). (“Angalau” hutafsiriwa kuwa alama “kubwa kuliko au sawa na”).

Zoezi\(\PageIndex{2}\)

mwalimu anahisi kwamba 15% ya wanafunzi kupata chini C juu ya mtihani wao wa mwisho. Yeye anaamua kuangalia mitihani ya mwisho (kuchaguliwa nasibu na kubadilishwa katika rundo baada ya kusoma) mpaka yeye anaona moja ambayo inaonyesha daraja chini C. tunataka kujua uwezekano kwamba mwalimu itakuwa na kuchunguza mitihani angalau kumi mpaka yeye anaona moja na daraja chini C. ni swali uwezekano gani alisema hesabu?

Jibu

\(P(x \leq 10)\)

Mfano\(\PageIndex{3}\)

Tuseme kwamba wewe ni kuangalia kwa mwanafunzi katika chuo yako ambaye anaishi ndani ya maili tano ya wewe. Unajua kwamba 55% ya wanafunzi 25,000 wanaishi ndani ya maili tano kati yenu. You nasibu kuwasiliana wanafunzi kutoka chuo mpaka mtu anasema yeye au yeye anaishi ndani ya maili tano ya wewe. Je! Ni uwezekano gani unahitaji kuwasiliana na watu wanne?

Hili ni tatizo la kijiometri kwa sababu unaweza kuwa na idadi ya kushindwa kabla ya kuwa na mafanikio moja unayotaka. Pia, uwezekano wa mafanikio unakaa sawa kila wakati unapomwomba mwanafunzi ikiwa anaishi ndani ya maili tano kati yenu. Hakuna idadi ya uhakika ya majaribio (idadi ya nyakati unazouliza mwanafunzi).

1. Hebu idadi\(X =\) ya ____________ lazima uulize ____________ moja anasema ndiyo.
2. Je! Maadili gani\(X\) huchukua?
3. Ni nini\(p\) na\(q\)?
4. Swali la uwezekano ni\(P(\) _______\()\).

Suluhisho

1. Hebu idadi\(X =\) ya wanafunzi lazima kuuliza mpaka mtu anasema ndiyo.
2. 1, 2, 3,..., (jumla ya idadi ya wanafunzi)
3. \(p = 0.55; q = 0.45\)
4. \(P(x = 4)\)

Zoezi\(\PageIndex{3}\)

Unahitaji kupata duka ambalo hubeba wino maalum wa printer. Unajua kwamba wa maduka ambayo hubeba wino wa printer, 10% yao hubeba wino maalum. Wewe nasibu wito kila duka mpaka mtu ana wino unahitaji. Ni nini\(p\) na\(q\)?

Jibu

\(p = 0.1\)

\(q = 0.9\)

Uthibitisho wa Jiometri:\(G =\) Geometric Probability Distribution Function

\(X \sim G(p)\)

Soma hii kama "\(X\)ni kutofautiana kwa random na usambazaji wa kijiometri.” Kipimo ni\(p\); uwezekano\(p =\) wa mafanikio kwa kila jaribio.

Mfano\(\PageIndex{4}\)

Fikiria kwamba uwezekano wa sehemu ya kompyuta isiyofaa ni 0.02. Vipengele vimechaguliwa kwa nasibu. Pata uwezekano kwamba kasoro ya kwanza inasababishwa na sehemu ya saba iliyojaribiwa. Je! Unatarajia vipengele ngapi kupima mpaka mtu atakapopatikana kuwa na kasoro?

Hebu\(X\) = idadi ya vipengele vya kompyuta vilivyojaribiwa mpaka kasoro la kwanza linapatikana.

\(X\)inachukua maadili 1, 2, 3,... wapi\(p = 0.02\). \(X \sim G(0.02)\)

Kupata\(P(x = 7)\). \(P(x = 7) = 0.0177\).

Ili kupata uwezekano kwamba\(x = 7\),

• Ingiza 2 ^nd, DISTRR
• Tembea chini na uchague geometpdf (
• Waandishi wa habari kuingia
• Ingiza 0.02, 7); waandishi wa habari kuingia ili uone matokeo:\(P(x = 7) = 0.0177\)

Ili kupata uwezekano kwamba\(x \leq 7\), fuata maelekezo sawa ILA chagua E: geometcdf kama kazi ya usambazaji.

Uwezekano kwamba sehemu ya saba ni kasoro ya kwanza ni 0.0177.

Grafu ya\(X \sim G(0.02)\) ni:

Kielelezo\(\PageIndex{1}\)

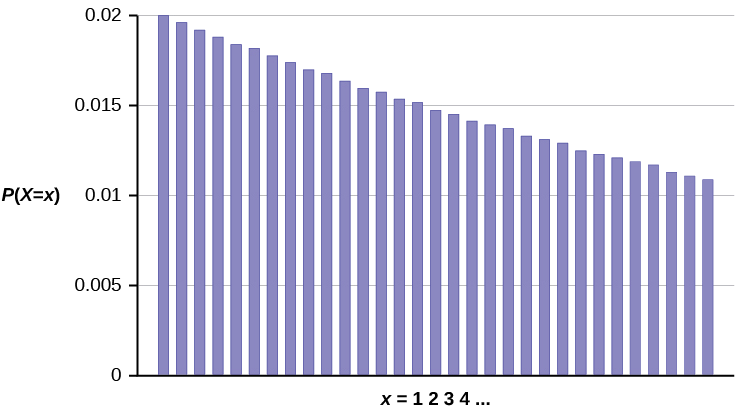
Y -axis ina uwezekano wa\(x\), ambapo idadi\(X =\) ya vipengele vya kompyuta kupimwa.

Idadi ya vipengele ambavyo ungependa kutarajia kupima mpaka utakapopata moja ya kwanza ya kasoro ni maana,\(\mu = 50\).

Fomu ya maana ni

\[\mu = \dfrac{1}{\text{p}} = \dfrac{1}{0.02} = 50\]

Fomu ya ugomvi ni

\[\sigma^{2} = \left(\dfrac{1}{p}\right)\left(\dfrac{1}{p} - 1 \right) = \left(\dfrac{1}{0.02}\right)\left(\dfrac{1}{0.02} - 1 \right) = 2,450\]

Kupotoka kwa kiwango ni

\[\sigma = \sqrt{\left(\dfrac{1}{p}\right)\left(\dfrac{1}{p} - 1\right)} = \sqrt{\left(\dfrac{1}{0.02}\right)\left(\dfrac{1}{0.02} - 1\right)} = 49.5\]

Zoezi\(\PageIndex{4}\)

Uwezekano wa fimbo ya chuma isiyofaa ni 0.01. Fimbo za chuma huchaguliwa kwa random. Pata uwezekano kwamba kasoro ya kwanza hutokea kwenye fimbo ya tisa ya chuma. Tumia calculator TI-83+ au TI-84 ili upate jibu.

Jibu

\(P(x = 9) = 0.0092\)

Mfano\(\PageIndex{5}\)

Hatari ya maisha ya kuendeleza saratani ya kongosho ni moja kati ya 78 (1.28%). Hebu idadi\(X =\) ya watu unayowauliza mpaka mtu anasema ana saratani ya kongosho. Kisha\(X\) ni discrete random variable na usambazaji kijiometri:\(X \sim G\left(\dfrac{1}{78}\right)\) au\(X \sim G(0.0128)\).

1. Je! Ni uwezekano gani wa kuuliza watu kumi kabla ya mtu kusema ana saratani ya kongosho?
2. Ni uwezekano gani kwamba lazima uulize watu 20?
3. Kupata (i) maana na (ii) kiwango kupotoka ya\(X\).

Jibu

1. \(P(x = 10) = \text{geometpdf}(0.0128, 10) = 0.0114\)
2. \(P(x = 20) = \text{geometpdf}(0.0128, 20) = 0.01\)
3. 1. Maana\(= \mu = \dfrac{1}{p} = \dfrac{1}{0.0128} = 78\)
   2. Mkengeuko\(= \sigma = \sqrt{\dfrac{1-p}{p^{2}}} = \sqrt{\dfrac{1-0.0128}{0.0128^{2}}} \approx 77.6234\)

Zoezi\(\PageIndex{5}\)

Kiwango cha kusoma na kuandika kwa taifa hupima uwiano wa watu wenye umri wa miaka 15 na zaidi ambao wanaweza kusoma na kuandika. Kiwango cha kusoma na kuandika kwa wanawake nchini Afghanistan ni 12%. Hebu idadi\(X =\) ya wanawake wa Afghanistan mnayowauliza mpaka mmoja atakaposema kwamba anajifunza.

1. Je, ni uwezekano wa usambazaji wa\(X\) nini?
2. Je! Ni uwezekano gani unawauliza wanawake watano kabla ya mtu kusema yeye anajifunza?
3. Je! Ni uwezekano gani unapaswa kuuliza wanawake kumi?
4. Kupata (i) maana na (ii) kiwango kupotoka ya\(X\).

Jibu

1. \(X \sim G(0.12)\)
2. \(P(x = 5) = \text{geometpdf}(0.12, 5) = 0.0720\)
3. \(P(x = 10) = \text{geometpdf}(0.12, 10) = 0.0380\)
4. 1. Maana\(= \mu = \dfrac{1}{p} = \dfrac{1}{0.12} \approx 3333\)
   2. Mkengeuko\(= \sigma = \dfrac{1-p}{p^{2}} = \dfrac{1-0.12}{0.12^{2}} \approx 7.8174\)

Marejeo

1. “Millennials: Picha ya Kizazi Next,” PewKituo cha Utafiti. Inapatikana mtandaoni kwenye www.pewsocialtrends.org/files... -to-change.pdf (ilifikia Mei 15, 2013).
2. “Millennials: ujasiri. Imeunganishwa. Fungua Badilisha.” Muhtasari wa Muhtasari na PewResearch Social & Mwelekeo wa Idadi Inapatikana mtandaoni kwenye http://www.pewsocialtrends.org/2010/...pen-to-change/ (imefikia Mei 15, 2013).
3. “Kuenea kwa VVU, jumla (% ya watu wenye umri wa miaka 15-49),” Benki ya Dunia, 2013. Inapatikana mtandaoni kwenye http://data.worldbank.org/indicator/...last&sort=desc (imefikia Mei 15, 2013).
4. Pryor, John H., Linda DeAngelo, Laura Palucki Blake, Sylvia Hurtado, Serge Tran. Freshman American: Kanuni za Taifa Fall 2011. Los Angeles: Programu ya Utafiti wa Taasisi ya Ushirika katika Taasisi ya Utafiti wa Elimu ya Juu katika UCLA Pia inapatikana mtandaoni kwenye http://heri.ucla.edu/PDFs/pubs/TFS/N...eshman2011.pdf (imefikia Mei 15, 2013).
5. “Muhtasari wa Tathmini ya Taifa ya Hatari na Matatizo 2007/8: maelezo ya Afghanistan,” Umoja wa Ulaya na Taasisi ya Icon. Inapatikana mtandaoni kwenye ec.europa.eu/europaid/where/... summary_en.pdf (imefikia Mei 15, 2013).
6. “World FactBook,” Central Intelligence Agency. Inapatikana mtandaoni kwenye https://www.cia.gov/library/publicat...k/geos/af.html (imefikia Mei 15, 2013).
7. “Taarifa za UNICEF kuhusu vituo vya Ujuzi wa Wanawake nchini Afghanistan vilivyoanzishwa ili kuwafundisha wanawake na wasichana ujuzi wa kusoma na kuandika msingi,” UNICEF Television. Video inapatikana mtandaoni kwenye http://www.unicefusa.org/assets/vide...y-centers.html (imefikia Mei 15, 2013).

Mapitio

Kuna sifa tatu za jaribio la kijiometri:

• Kuna majaribio moja au zaidi ya Bernoulli na kushindwa yote isipokuwa ya mwisho, ambayo ni mafanikio.
• Kwa nadharia, idadi ya majaribio inaweza kuendelea milele. Lazima iwe na angalau jaribio moja.
• Uwezekano\(p\),, wa mafanikio na uwezekano,\(q\), wa kushindwa ni sawa kwa kila jaribio.

Katika majaribio ya kijiometri, kufafanua kipekee random variable\(X\) kama idadi ya majaribio ya kujitegemea mpaka mafanikio ya kwanza. Tunasema kuwa\(X\) ina usambazaji wa kijiometri na kuandika\(X \sim G(p)\) wapi\(p\) uwezekano wa mafanikio katika jaribio moja. Maana ya usambazaji wa kijiometri\(X \sim G(p)\) ni\(\mu = \dfrac{1-p}{p^{2}} = \sqrt{\dfrac{1}{p}\left(\dfrac{1}{p} - 1\right)}\).

Mapitio ya Mfumo

\(X \sim G(p)\)ina maana kwamba discrete random variable\(X\) ina kijiometri uwezekano usambazaji na uwezekano wa mafanikio katika kesi moja\(p\).

\(X =\)idadi ya majaribio ya kujitegemea mpaka mafanikio ya kwanza

\(X\)inachukua maadili\(x = 1, 2, 3, \dotsc\)

\(p =\)uwezekano wa mafanikio kwa jaribio lolote

\(q =\)uwezekano wa kushindwa kwa jaribio lolote\(p + q = 1\)

\(q = 1 – p\)

Maana ni\(\mu = \dfrac{1}{p}\).

Kupotoka kwa kiwango ni\(\sigma = \dfrac{1-p}{p^{2}} = \sqrt{\dfrac{1}{p}\left(\dfrac{1}{p} - 1\right)}\).

Tumia maelezo yafuatayo ili kujibu mazoezi sita yafuatayo: Taasisi ya Utafiti wa Elimu ya Juu katika UCLA ilikusanya data kutoka 203,967 zinazoingia mara ya kwanza, freshmen ya muda kutoka vyuo vikuu vya miaka 270 na vyuo vikuu nchini Marekani 71.3% ya wanafunzi hao walijibu kwamba, ndiyo, wanaamini kuwa wanandoa wa jinsia moja wanapaswa kuwa na haki ya hali ya kisheria ya ndoa. Tuseme kwamba wewe nasibu kuchagua freshman kutoka utafiti mpaka kupata mtu ambaye anajibu “ndiyo.” Una nia ya idadi ya freshmen lazima kuuliza.

Zoezi 4.5.6

Kwa maneno, kufafanua variable random\(X\).

Jibu

\(X =\)idadi ya freshmen waliochaguliwa kutoka utafiti mpaka mmoja alijibu “ndiyo” kwamba wanandoa wa jinsia moja wanapaswa kuwa na haki ya hali ya kisheria ya ndoa.

Zoezi 4.5.7

\(X \sim\)_____ (_____, _____)

Zoezi 4.5.8

Nini maadili gani variable random\(X\) kuchukua?

Jibu

1,2,...

Zoezi 4.5.9

Kujenga uwezekano usambazaji kazi (PDF). Acha saa\(x = 6\).

\(x\)	\(P(x)\)
\ (x\) ">1	\ (P (x)\) ">
\ (x\) "> 2	\ (P (x)\) ">
\ (x\) ">3	\ (P (x)\) ">
\ (x\) ">4	\ (P (x)\) ">
\ (x\) "> 5	\ (P (x)\) ">
\ (x\) ">6	\ (P (x)\) ">

Zoezi 4.5.10

Kwa wastani (\(\mu\)), ni wangapi freshmen ungependa kuuliza mpaka umepata mtu anayejibu “ndiyo?”

Jibu

1.4

Zoezi 4.5.11

Je! Ni uwezekano gani kwamba unahitaji kuuliza chini ya freshmen tatu?

maelezo ya chini

¹” Kuenea kwa VVU, jumla (% ya watu wenye umri wa miaka 15-49),” Benki ya Dunia, 2013. Inapatikana mtandaoni kwenye http://data.worldbank.org/indicator/...pi_data_value - last&sort=desc (imefikia Mei 15, 2013).

faharasa

Usambazaji wa Jiometri

kipekee random variable (RV) inayotokana na majaribio Bernoulli; majaribio ni mara kwa mara mpaka mafanikio ya kwanza. Vigezo vya kijiometri\(X\) hufafanuliwa kama idadi ya majaribio hadi mafanikio ya kwanza. Nukuu:\(X \sim G(p)\). maana ni\(\mu = \dfrac{1}{p}\) na kupotoka kiwango ni\(\sigma =\)

\[\sqrt{\dfrac{1}{p}\left(\dfrac{1}{p} - 1\right)}\]

. Uwezekano wa\(x\) kushindwa hasa kabla ya mafanikio ya kwanza hutolewa na formula:\(P(X = x) = p(1 –p)^{x-1}\).

Kijiometri majaribio

jaribio la takwimu na mali zifuatazo:

1. Kuna majaribio moja au zaidi ya Bernoulli na kushindwa yote isipokuwa ya mwisho, ambayo ni mafanikio.
2. Kwa nadharia, idadi ya majaribio inaweza kuendelea milele. Lazima iwe na angalau jaribio moja.
3. Uwezekano,\(p\), wa mafanikio na uwezekano,\(q\), wa kushindwa haubadilika kutoka jaribio hadi jaribio.