4.4: Usambazaji wa Binomial

Usambazaji wa binomial mara nyingi hutumiwa kutengeneza idadi ya mafanikio katika sampuli ya ukubwa\(n\) inayotolewa na uingizwaji kutoka kwa idadi ya ukubwa\(N\).

Tabia tatu za jaribio la binomial

1. Kuna idadi maalum ya majaribio. Fikiria majaribio kama marudio ya jaribio. Barua hiyo\(n\) inaashiria idadi ya majaribio.
2. Kuna matokeo mawili tu yanayowezekana, inayoitwa “mafanikio” na “kushindwa,” kwa kila jaribio. Barua hiyo\(p\) inaashiria uwezekano wa mafanikio kwenye jaribio moja, na\(q\) inaashiria uwezekano wa kushindwa kwenye jaribio moja. \(p + q = 1\).
3. \(n\)Majaribio ni ya kujitegemea na yanarudiwa kwa kutumia hali sawa. Kwa sababu\(n\) majaribio yanajitegemea, matokeo ya jaribio moja hayasaidia kutabiri matokeo ya jaribio jingine. Njia nyingine ya kusema hii ni kwamba kwa kila jaribio la mtu binafsi\(p\), uwezekano, wa mafanikio na uwezekano\(q\), wa kushindwa kubaki sawa. Kwa mfano, nasibu nadhani katika swali la kweli la uongo la takwimu lina matokeo mawili tu. Ikiwa mafanikio ni nadhani kwa usahihi, basi kushindwa kunafikiri vibaya. Tuseme Joe daima nadhani kwa usahihi juu ya takwimu yoyote ya kweli ya uongo swali na uwezekano\(p = 0.6\). Kisha,\(q = 0.4\). Hii ina maana kwamba kwa kila takwimu za uongo swali la Joe anajibu, uwezekano wake wa mafanikio (\(p = 0.6\)) na uwezekano wake wa kushindwa (\(q = 0.4\)) kubaki sawa.

Matokeo ya jaribio la binomial yanafaa usambazaji wa uwezekano wa binomial. kutofautiana kwa random idadi\(X =\) ya mafanikio yaliyopatikana katika majaribio ya\(n\) kujitegemea. maana,\(\mu\), na ugomvi,\(\sigma^{2}\), kwa ajili ya usambazaji wa uwezekano wa binomial ni

\[\mu = np\]

na

\[\sigma^{2} = npq.\]

kupotoka kiwango,\(\sigma\), ni basi

\[\sigma = \sqrt{npq}.\]

Jaribio lolote ambalo lina sifa mbili na tatu na wapi\(n = 1\) linaitwa kesi ya Bernoulli (jina lake baada ya Jacob Bernoulli ambaye, mwishoni mwa miaka ya 1600, alisoma sana). Jaribio la binomial hufanyika wakati idadi ya mafanikio inahesabiwa katika majaribio moja au zaidi ya Bernoulli.

Mfano\(\PageIndex{1}\)

Katika Chuo cha ABC, kiwango cha uondoaji kutoka kozi ya msingi ya fizikia ni 30% kwa muda wowote. Hii ina maana kwamba, kwa muda wowote, 70% ya wanafunzi hukaa darasani kwa muda wote. “Mafanikio” yanaweza kuelezwa kama mtu ambaye aliondoka. variable random idadi\(X =\) ya wanafunzi ambao kujiondoa kutoka nasibu kuchaguliwa msingi fizikia darasa.

Zoezi\(\PageIndex{1}\)

Bodi ya afya ya serikali ina wasiwasi juu ya kiasi cha matunda inapatikana katika chakula cha mchana cha shule. Asilimia arobaini na nane ya shule katika hali hutoa matunda katika chakula cha mchana kila siku. Hii ina maana kwamba 52% hawana. Je! “Mafanikio” yatakuwa katika kesi hii?

Jibu

shule ambayo inatoa matunda katika chakula cha mchana kila siku

Mfano\(\PageIndex{2}\)

Tuseme wewe kucheza mchezo kwamba unaweza tu ama kushinda au kupoteza. uwezekano kwamba wewe kushinda mchezo wowote ni 55%, na uwezekano kwamba kupoteza ni 45%. Kila mchezo kucheza ni huru. Kama wewe kucheza mchezo 20 mara, kuandika kazi inayoelezea uwezekano kwamba wewe kushinda 15 ya 20 mara. Hapa, ikiwa unafafanua\(X\) kama idadi ya mafanikio, kisha\(X\) inachukua maadili 0, 1, 2, 3,..., 20. Uwezekano wa mafanikio ni\(p = 0.55\). Uwezekano wa kushindwa ni\(q = 0.45\). Idadi ya majaribio ni\(n = 20\). swali uwezekano inaweza kuwa alisema hesabu kama\(P(x = 15)\).

Zoezi\(\PageIndex{2}\)

Mkufunzi anafundisha dolphin kufanya tricks. Uwezekano kwamba dolphin hufanya hila kwa ufanisi ni 35%, na uwezekano kwamba dolphin haifanikiwa kufanya hila ni 65%. Kati ya majaribio 20, unataka kupata uwezekano kwamba dolphin inafanikiwa mara 12. Hali uwezekano swali hesabu.

Jibu

\(P(x = 12)\)

Mfano\(\PageIndex{3}\)

Sarafu ya haki imepigwa mara 15. Kila flip ni huru. Je! Ni uwezekano gani wa kupata vichwa zaidi ya kumi? Hebu idadi\(X =\) ya vichwa katika flips 15 ya sarafu ya haki. \(X\)inachukua maadili 0, 1, 2, 3,..., 15. Tangu sarafu ni haki,\(p = 0.5\) na\(q = 0.5\). Idadi ya majaribio ni\(n = 15\). Hali uwezekano swali hesabu.

Suluhisho

\(P(x > 10)\)

Zoezi\(\PageIndex{4}\)

Haki, sita upande mmoja kufa ni akavingirisha mara kumi. Kila roll ni huru. Unataka kupata uwezekano wa kupiga moja zaidi ya mara tatu. Hali uwezekano swali hesabu.

Jibu

\(P(x > 3)\)

Mfano\(\PageIndex{5}\)

Takriban asilimia 70 ya wanafunzi wa takwimu hufanya kazi zao za nyumbani kwa wakati ili kukusanywa na kufuzu. Kila mwanafunzi anafanya kazi za nyumbani kwa kujitegemea. Katika darasa la takwimu la wanafunzi wa 50, ni uwezekano gani kwamba angalau 40 watafanya kazi zao za nyumbani kwa wakati? Wanafunzi huchaguliwa nasibu.

1. Hili ni tatizo la binomial kwa sababu kuna mafanikio tu au __________, kuna idadi maalum ya majaribio, na uwezekano wa mafanikio ni 0.70 kwa kila jaribio.
2. Ikiwa tunavutiwa na idadi ya wanafunzi wanaofanya kazi zao za nyumbani kwa wakati, basi tunafafanuzaje\(X\)?
3. Je! Maadili gani\(x\) huchukua?
4. “Kushindwa,” kwa maneno?
5. Ikiwa\(p + q = 1\), basi ni nini\(q\)?
6. Maneno “angalau” hutafsiri kama aina gani ya usawa kwa swali la uwezekano\(P(x\) ____\(40\)).

Suluhisho

1. kutofaulu
2. \(X\)= idadi ya wanafunzi wa takwimu wanaofanya kazi zao za nyumbani kwa wakati
3. 0, 1, 2,..., 50
4. Kushindwa hufafanuliwa kama mwanafunzi asiyekamilisha kazi yake ya nyumbani kwa wakati. Uwezekano wa mafanikio ni\(p = 0.70\). Idadi ya majaribio ni\(n = 50\).
5. \(q = 0.30\)
6. kubwa kuliko au sawa na (\(\geq\)). Swali la uwezekano ni\(P(x \geq 40)\).

Zoezi\(\PageIndex{5}\)

Asilimia sitini na tano ya watu hupitia mtihani wa dereva wa serikali kwenye jaribio la kwanza. Kikundi cha watu 50 ambao wamechukua mtihani wa dereva huchaguliwa kwa nasibu. Kutoa sababu mbili kwa nini hii ni tatizo la binomial.

Jibu

Hili ni tatizo la binomial kwa sababu kuna mafanikio tu au kushindwa, na kuna idadi ya uhakika ya majaribio. Uwezekano wa mafanikio unakaa sawa kwa kila jaribio.

Uthibitisho wa Binomial:\(B =\) Binomial Probability Distribution Function

\[X \sim B(n, p)\]

Soma hii kama "\(X\)ni variable random na usambazaji binomial.” Vigezo ni\(n\) na\(p\);\(n =\) idadi ya majaribio,\(p =\) uwezekano wa mafanikio katika kila kesi.

Mfano\(\PageIndex{6}\)

Imesemekana kuwa takriban 41% ya wafanyakazi wazima wana diploma ya shule ya sekondari lakini hawafuatii elimu yoyote zaidi. Ikiwa wafanyakazi wazima 20 wanachaguliwa kwa nasibu, pata uwezekano wa kuwa zaidi ya 12 kati yao wana diploma ya shule ya sekondari lakini hawafuatii elimu yoyote zaidi. Ni wafanyakazi wangapi wazima ambao unatarajia kuwa na diploma ya shule ya sekondari lakini hawafuatii elimu yoyote zaidi?

Hebu\(X\) = idadi ya wafanyakazi ambao wana diploma ya shule ya sekondari lakini hawafuatii elimu yoyote zaidi.

\(X\)inachukua maadili 0, 1, 2,..., 20 ambapo\(n = 20, p = 0.41\), na\(q = 1 – 0.41 = 0.59\). \(X \sim B(20, 0.41)\)

Kupata\(P(x \leq 12)\). \(P(x \leq 12) = 0.9738\). (calculator au kompyuta)

Nenda katika 2 ^na Distr. Syntax kwa maelekezo ni kama ifuatavyo:

Ili kuhesabu (\(x = \text{value}): \text{binompdf}(n, p, \text{number}\)) ikiwa “nambari” imesalia nje, matokeo ni meza ya uwezekano wa binomial.

Ili kuhesabu\(P(x \leq \text{value}): \text{binomcdf}(n, p, \text{number})\) ikiwa “nambari” imesalia nje, matokeo yake ni meza ya uwezekano wa binomial.

Kwa tatizo hili: Baada ya wewe ni katika 2 ^nd DISTR, mshale chini ya binomcdf. Bonyeza kuingia. Ingiza 20,0.41,12). Matokeo yake ni\(P(x \leq 12) = 0.9738\).

Ikiwa unataka kupata\(P(x = 12)\), tumia pdf (binompdf). Ikiwa unataka kupata\(P(x > 12)\), tumia\(1 - \text{binomcdf}(20,0.41,12)\).

Uwezekano wa kuwa wafanyakazi zaidi 12 wana diploma ya shule ya sekondari lakini hawafuati elimu yoyote zaidi ni 0.9738.

Grafu ya\(X \sim B(20, 0.41)\) ni kama ifuatavyo:

Kielelezo\(\PageIndex{1}\): grafu ya\(X \sim B(20, 0.41)\).

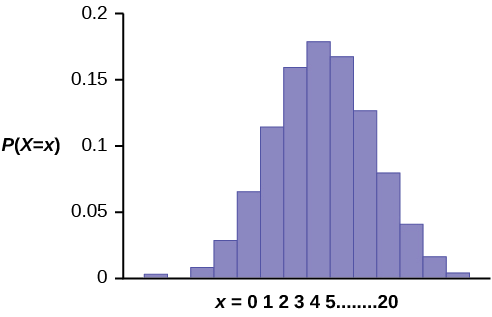
Y -axis ina uwezekano wa\(x\), where \(X =\) the number of workers who have only a high school diploma.

Idadi ya wafanyakazi wazima ambao unatarajia kuwa na diploma ya shule ya sekondari lakini si kufuata elimu yoyote zaidi ni maana,\(\mu = np = (20)(0.41) = 8.2\).

Fomu ya ugomvi ni\(\sigma^{2} = npq\). Kupotoka kwa kiwango ni\(\sigma = \sqrt{npq}\).

\[\sigma = \sqrt{(20)(0.41)(0.59)} = 2.20.\]

Zoezi 4.4.5

Kuhusu 32% ya wanafunzi kushiriki katika mpango wa kujitolea jamii nje ya shule. Kama 30 wanafunzi ni kuchaguliwa kwa random, kupata uwezekano kwamba wengi 14 wao kushiriki katika mpango wa kujitolea jamii nje ya shule. Tumia calculator TI-83+ au TI-84 ili upate jibu.

Jibu

\(P(x \leq 14) = 0.9695\)

Mfano\(\PageIndex{7}\)

Katika orodha ya vifaa vya sanaa ya Jerry ya Artarama ya 2013, kuna kurasa 560. Kurasa nane zinajumuisha wasanii wa saini. Tuseme sisi nasibu sampuli 100 kurasa. Hebu idadi\(X =\) ya kurasa zinazoonyesha wasanii wa saini.

1. Je! Maadili gani\(x\) huchukua?
2. Usambazaji wa uwezekano ni nini? Pata uwezekano wafuatayo:
   1. uwezekano kwamba kurasa mbili kipengele wasanii sahihi
   2. uwezekano kwamba katika zaidi ya kurasa sita kipengele wasanii saini
   3. uwezekano kwamba zaidi ya kurasa tatu kipengele wasanii sahihi.
3. Kutumia formula, hesabu (i) maana na (ii) kupotoka kwa kiwango.

Jibu

1. \(x = 0, 1, 2, 3, 4, 5, 6, 7, 8\)
2. \(X \sim B(100,8560)(100,8560)\)
   1. \(P(x = 2) = \text{binompdf}\left(100,\dfrac{8}{560},2\right) = 0.2466\)
   2. \(P(x \leq 6) = \text{binomcdf}\left(100,\dfrac{8}{560},6\right) = 0.9994\)
   3. \(P(x > 3) = 1 – P(x \leq 3) = 1 – \text{binomcdf}\left(100,\dfrac{8}{560},3\right) = 1 – 0.9443 = 0.0557\)
3. 1. Maana\(= np = (100)\left(\dfrac{8}{560}\right) = \dfrac{800}{560} \approx 1.4286\)
   2. Mkengeuko\(= \sqrt{npq} = \sqrt{(100)\left(\dfrac{8}{560}\right)\left(\dfrac{552}{560}\right)} \approx 1.1867\)

Zoezi\(\PageIndex{7}\)

Kwa mujibu wa uchaguzi wa Gallup, 60% ya watu wazima wa Marekani wanapendelea kuokoa zaidi ya matumizi. Hebu\(X\) = idadi ya watu wazima wa Marekani nje ya sampuli ya random ya 50 ambao wanapendelea kuokoa matumizi.

1. Je, ni uwezekano wa usambazaji kwa\(X\) nini?
2. Tumia calculator yako ili kupata probabilities zifuatazo:
   1. uwezekano kwamba watu wazima 25 katika sampuli wanapendelea kuokoa juu ya matumizi
   2. uwezekano kwamba watu wazima zaidi 20 wanapendelea kuokoa
   3. uwezekano kwamba watu wazima zaidi ya 30 wanapendelea kuokoa
3. Kwa kutumia formula, mahesabu ya (i) maana na (ii) kiwango kupotoka ya\(X\).

Jibu

1. \(X \sim B(50, 0.6)\)
2. Kutumia TI-83, 83+, 84 calculator na maelekezo kama ilivyoelezwa katika Mfano:
   1. \(P(x = 25) = \text{binompdf}(50, 0.6, 25) = 0.0405\)
   2. \(P(x \leq 20) = \text{binomcdf}(50, 0.6, 20) = 0.0034\)
   3. \((x > 30) = 1 - \text{binomcdf}(50, 0.6, 30) = 1 – 0.5535 = 0.4465\)
3. 1. Maana\(= np = 50(0.6) = 30\)
   2. Mkengeuko\(= \sqrt{npq} = \sqrt{50(0.6)(0.4)} \approx 3.4641\)

Mfano\(\PageIndex{8}\)

Hatari ya maisha ya kuendeleza saratani ya kongosho ni moja kati ya 78 (1.28%). Tuseme sisi nasibu sampuli 200 watu. Hebu\(X\) = idadi ya watu ambao wataendeleza saratani ya kongosho.

1. Je, ni uwezekano wa usambazaji kwa\(X\) nini?
2. Kwa kutumia formula, mahesabu ya (i) maana na (ii) kiwango kupotoka ya\(X\).
3. Tumia calculator yako ili kupata uwezekano kwamba watu wengi nane kuendeleza kansa ya kongosho
4. Je, kuna uwezekano zaidi kwamba watu watano au sita wataendeleza saratani ya kongosho? Thibitisha jibu lako kwa nambari.

Jibu

1. \(X \sim B(200, 0.0128)\)
2. 1. Maana\(= np = 200(0.0128) = 2.56\)
   2. Mkengeuko\(= \sqrt{npq} = \sqrt{(200)(0.0128)(0.9872)} \approx 1.5897\)
3. Kutumia TI-83, 83+, 84 calculator na maelekezo kama ilivyoelezwa katika Mfano:
   \(P(x \leq 8) = \text{binomcdf}(200, 0.0128, 8) = 0.9988\)
4. \(P(x = 5) = \text{binompdf}(200, 0.0128, 5) = 0.0707\)
   \(P(x = 6) = \text{binompdf}(200, 0.0128, 6) = 0.0298\)
   Hivyo\(P(x = 5) > P(x = 6)\), kuna uwezekano mkubwa kuwa watu watano wataendeleza saratani kuliko sita.

Zoezi\(\PageIndex{8}\)

Wakati wa msimu wa kawaida wa NBA wa 2013, DeAndre Jordan wa Los Angeles Clippers alikuwa na kiwango cha juu cha kukamilika kwa lengo la uwanja katika ligi hiyo. DeAndre alifunga na 61.3% ya shots zake. Tuseme unachagua sampuli ya random ya shots 80 zilizofanywa na DeAndre wakati wa msimu wa 2013. Hebu idadi\(X =\) ya shots kwamba alifunga pointi.

1. Je, ni uwezekano wa usambazaji kwa\(X\) nini?
2. Kwa kutumia formula, mahesabu ya (i) maana na (ii) kiwango kupotoka ya\(X\).
3. Tumia calculator yako ili kupata uwezekano kwamba DeAndre alifunga na 60 ya shots hizi.
4. Pata uwezekano kwamba DeAndre alifunga na zaidi ya 50 ya shots hizi.

Jibu

1. \(X \sim B(80, 0.613)\)
2. 1. Maana\(= np = 80(0.613) = 49.04\)
   2. Mkengeuko\(= \sqrt{npq} = \sqrt{80(0.613)(0.387)} \approx 4.3564\)
3. Kutumia TI-83, 83+, 84 calculator na maelekezo kama ilivyoelezwa katika Mfano:
   \(P(x = 60) = \text{binompdf}(80, 0.613, 60) = 0.0036\)
4. \(P(x > 50) = 1 – P(x \leq 50) = 1 – \text{binomcdf}(80, 0.613, 50) = 1 – 0.6282 = 0.3718\)

Mfano\(\PageIndex{9}\)

Mfano unaofuata unaeleza tatizo ambalo si binomial. Inakiuka hali ya uhuru. ABC College ina kamati ya ushauri wa wanafunzi iliyoundwa na wafanyakazi kumi na wanafunzi sita. Kamati inataka kuchagua mwenyekiti na rekodi. Je, ni uwezekano gani kwamba mwenyekiti na rekodi ni wanafunzi wote? Majina ya wajumbe wote wa kamati huwekwa ndani ya sanduku, na majina mawili hutolewa bila uingizwaji. Jina la kwanza lililotolewa huamua mwenyekiti na jina la pili rekodi. Kuna majaribio mawili. Hata hivyo, majaribio hayajitegemea kwa sababu matokeo ya jaribio la kwanza huathiri matokeo ya jaribio la pili. Uwezekano wa mwanafunzi kwenye sare ya kwanza ni\(\dfrac{6}{16}\). Uwezekano wa mwanafunzi kwenye sare ya pili ni\(\dfrac{5}{15}\), wakati kuteka kwanza kumchagua mwanafunzi. Uwezekano ni\(\dfrac{6}{15}\), wakati sare ya kwanza huchagua mfanyakazi. Uwezekano wa kuchora jina la mwanafunzi hubadilika kwa kila majaribio na, kwa hiyo, inakiuka hali ya uhuru.

Zoezi\(\PageIndex{9}\)

Timu ya Lacrosse inachagua nahodha. Majina ya wazee wote huwekwa kwenye kofia, na watatu wa kwanza ambao hutolewa watakuwa maakida. Majina hayajabadilishwa mara wanapochorwa (mtu mmoja hawezi kuwa maakida wawili). Unataka kuona kama maakida wote kucheza nafasi sawa. Hali kama hii ni binomial au la na kusema kwa nini.

Jibu

Hii si binomial kwa sababu majina hayajabadilishwa, ambayo ina maana mabadiliko ya uwezekano kwa kila wakati jina linatolewa. Hii inakiuka hali ya uhuru.

Marejeo

1. “Upatikanaji wa umeme (% ya idadi ya watu),” Benki ya Dunia, 2013. Inapatikana mtandaoni kwenye http://data.worldbank.org/indicator/...first&sort=asc (imefikia Mei 15, 2015).
2. “Elimu ya Umbali.” Wikipedia. Inapatikana mtandaoni kwenye http://en.Wikipedia.org/wiki/Distance_education (imefikia Mei 15, 2013).
3. “NBA Takwimu - 2013, "ESPN NBA, 2013. Inapatikana mtandaoni kwenye http://espn.go.com/nba/statistics/_/seasontype/2 (imefikia Mei 15, 2013).
4. Newport, Frank. “Wamarekani Bado Kufurahia Kuokoa Badala ya Matumizi: Wachache idadi ya watu tofauti kuonekana katika maoni haya zaidi ya mapato,” GALLUP® Uchumi, 2013. Inapatikana mtandaoni kwenye http://www.gallup.com/poll/162368/am... -spending.aspx (ilifikia Mei 15, 2013).
5. Pryor, John H., Linda DeAngelo, Laura Palucki Blake, Sylvia Hurtado, Serge Tran. Freshman American: Kanuni za Taifa Fall 2011. Los Angeles: Programu ya Utafiti wa Taasisi ya Ushirika katika Taasisi ya Utafiti wa Elimu ya Juu katika UCLA Pia inapatikana mtandaoni kwenye http://heri.ucla.edu/PDFs/pubs/TFS/N...eshman2011.pdf (imefikia Mei 15, 2013).
6. “World FactBook,” Central Intelligence Agency. Inapatikana mtandaoni kwenye https://www.cia.gov/library/publicat...k/geos/af.html (imefikia Mei 15, 2013).
7. “Takwimu muhimu kuhusu saratani ya kongosho ni nini?” American Cancer Society, 2013. Inapatikana mtandaoni kwenye www.cancer.org/cancer/pancrea... takwimu muhimu (zimefikiwa Mei 15, 2013).

Mapitio

Jaribio la takwimu linaweza kuhesabiwa kama jaribio la binomial ikiwa hali zifuatazo zinakabiliwa:

Kuna idadi maalum ya majaribio,\(n\).

Kuna matokeo mawili tu yanayowezekana, inayoitwa “mafanikio” na, “kushindwa” kwa kila jaribio. Barua hiyo\(p\) inaashiria uwezekano wa mafanikio kwenye jaribio moja na\(q\) inaashiria uwezekano wa kushindwa kwenye jaribio moja.

\(n\)Majaribio ni ya kujitegemea na yanarudiwa kwa kutumia hali sawa.

Matokeo ya jaribio la binomial yanafaa usambazaji wa uwezekano wa binomial. kutofautiana kwa random idadi\(X =\) ya mafanikio yaliyopatikana katika majaribio ya\(n\) kujitegemea. Maana ya\(X\) inaweza kuhesabiwa kwa kutumia formula\(\mu = np\), na kupotoka kwa kawaida hutolewa na formula\(\sigma = \sqrt{npq}\).

Mapitio ya Mfumo

• \(X \sim B(n, p)\)ina maana kwamba kipekee random variable\(X\) ina binomial uwezekano usambazaji na\(n\) majaribio na uwezekano wa mafanikio\(p\).
• \(X =\)idadi ya mafanikio katika majaribio ya\(n\) kujitegemea
• \(n =\)idadi ya majaribio ya kujitegemea
• \(X\)inachukua maadili\(x = 0, 1, 2, 3, \dotsc, n\)
• \(p =\)uwezekano wa mafanikio kwa jaribio lolote
• \(q =\)uwezekano wa kushindwa kwa jaribio lolote
• \(p + q = 1\)
• \(q = 1 – p\)

Maana ya\(X\) ni\(\mu = np\). kupotoka kiwango cha\(X\) ni\(\sigma = \sqrt{npq}\).

Tumia maelezo yafuatayo ili kujibu mazoezi nane yafuatayo: Taasisi ya Utafiti wa Elimu ya Juu katika UCLA ilikusanya data kutoka 203,967 zinazoingia mara ya kwanza, freshmen ya muda wote kutoka vyuo vikuu vya miaka 270 na vyuo vikuu nchini Marekani 71.3% ya wanafunzi hao walijibu kwamba, ndiyo, wanaamini kuwa wanandoa wa jinsia moja wanapaswa kuwa na haki ya hali ya kisheria ya ndoa. Tuseme kwamba wewe nasibu kuchukua nane mara ya kwanza, freshmen wakati wote kutoka utafiti. Unavutiwa na idadi inayoamini kwamba wanandoa wa jinsia moja wanapaswa kuwa na haki ya hali ya ndoa ya kisheria.

Zoezi 4.4.9

Kwa maneno, kufafanua variable random\(X\).

Jibu

\(X =\)nambari inayojibu “ndiyo”

Zoezi 4.4.10

\(X \sim\)_____ (_____, _____)

Zoezi 4.4.11

Nini maadili gani variable random\(X\) kuchukua?

Jibu

0, 1, 2, 3, 4, 5, 6, 7, 8

Zoezi 4.4.12

Kujenga uwezekano usambazaji kazi (PDF).

\(x\)	\(P(x)\)

Zoezi 4.4.13

Kwa wastani (\(\mu\)), ngapi ungependa kutarajia kujibu ndiyo?

Jibu

5.7

Zoezi 4.4.14

Je, ni kiwango kupotoka (\(\sigma\))?

Zoezi 4.4.15

Je! Ni uwezekano gani kwamba zaidi ya watano wa freshmen wanajibu “ndiyo”?

Jibu

0.4151

Zoezi 4.4.16

Je! Ni uwezekano gani kwamba angalau wawili wa freshmen wanajibu “ndiyo”?

faharasa

Jaribio la Binomial

jaribio la takwimu ambalo linatimiza masharti matatu yafuatayo:

1. Kuna idadi maalum ya majaribio,\(n\).
2. Kuna matokeo mawili tu yanayowezekana, inayoitwa “mafanikio” na, “kushindwa,” kwa kila jaribio. Barua hiyo\(p\) inaashiria uwezekano wa mafanikio kwenye jaribio moja, na\(q\) inaashiria uwezekano wa kushindwa kwenye jaribio moja.
3. \(n\)Majaribio ni ya kujitegemea na yanarudiwa kwa kutumia hali sawa.

Bernoulli majaribio

jaribio la sifa zifuatazo:

1. Kuna matokeo mawili tu yanayowezekana inayoitwa “mafanikio” na “kushindwa” kwa kila jaribio.
2. Uwezekano\(p\) wa mafanikio ni sawa kwa jaribio lolote (hivyo uwezekano\(q = 1 − p\) wa kushindwa ni sawa kwa jaribio lolote).

Usambazaji wa Uwezekano wa Binomial

kipekee random variable (RV) inayotokana na majaribio Bernoulli; kuna idadi fasta,\(n\), ya majaribio ya kujitegemea. “Independent” inamaanisha kwamba matokeo ya jaribio lolote (kwa mfano, jaribio moja) haliathiri matokeo ya majaribio yafuatayo, na majaribio yote yanafanyika chini ya hali sawa. Chini ya hali hizi RV binomial\(X\) inaelezwa kama idadi ya mafanikio katika\(n\) majaribio. Nukuu ni:\(X ~ B(n, p)\). Maana ni\(\mu = np\) na kupotoka kwa kiwango ni\(\sigma = \sqrt{npq}\). Uwezekano wa\(x\) mafanikio hasa katika\(n\) majaribio ni
\(P(X = x) = {n \choose x}p^{x}q^{n-x}\).