11.E: Grafu (Mazoezi)

Last updated

Nov 1, 2022
Page ID
173377
Save as PDF
- 11.8: Kuelewa mteremko wa Line (Sehemu ya 2)
- 11.S: Grafu (Muhtasari)

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

11.1 - Tumia Mfumo wa Kuratibu wa Rectangular

Plot Pointi katika mfumo wa Kuratibu Rectangular

Katika mazoezi yafuatayo, njama kila hatua katika mfumo wa kuratibu mstatili.

(1, 3), (3, 1)
(2, 5), (5, 2)

Katika mazoezi yafuatayo, njama kila hatua katika mfumo wa kuratibu mstatili na kutambua quadrant ambayo hatua iko.

(a) (-1, -5) (b) (1-3, 4) (c) (2, 1-3) (d) $\left(1, \dfrac{5}{2}\right)$
(a) (3, -1) (b) (-4, -1) (c) (-5, 4) (d) $\left(2, \dfrac{10}{3}\right)$

Tambua Pointi kwenye Grafu

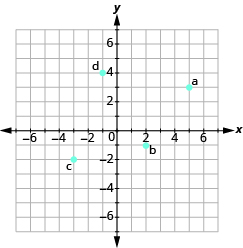
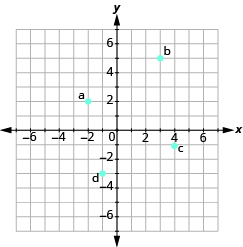
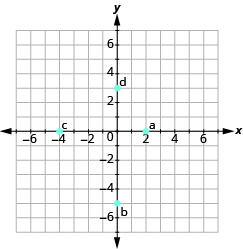
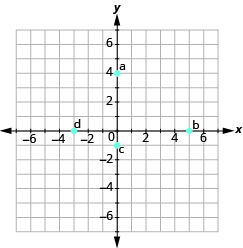
Katika mazoezi yafuatayo, jina la jozi iliyoamriwa ya kila hatua iliyoonyeshwa kwenye mfumo wa kuratibu mstatili.

$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. “a” imepangwa saa 5, 3, “b” saa 2, -1, “c” saa -3, -2, na “d” saa -1,4.$
$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. “a” imepangwa saa -2, 2, “b” saa 3, 5, “c” saa 4, -1, na “d” saa -1,3.$
$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. “a” imepangwa saa 2, 0, “b” saa 0, -5, “c” saa -4,0, na “d” saa 0,3.$
$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. “a” imepangwa saa 0, 4, “b” saa 5, 0, “c” saa 0, -1, na “d” saa -3,0.$

Thibitisha Ufumbuzi wa Equation katika Vigezo viwili

Katika mazoezi yafuatayo, tafuta jozi zilizoamriwa ambazo ni ufumbuzi wa equation iliyotolewa.

5x + y = 10
1. (5, 1)
2. (2, 0)
3. (4, -10)
y = 6x - 2
1. (1, 4)
2. $\left(\dfrac{1}{3} , 0\right)$
3. (6,-2)

Jaza Jedwali la Ufumbuzi wa Equation ya Mstari katika Vigezo viwili

Katika mazoezi yafuatayo, jaza meza ili kupata ufumbuzi kwa kila equation linear.

y = 4x - 1

x	y	(x, y)
0
1
-2

y = $− \dfrac{1}{2}$ x + 3

x	y	(x, y)
0
1
-2

x + 2y = 5

x	y	(x, y)
	0
1
-1

3x - 2y = 6

x	y	(x, y)
0
	0
-2

Pata ufumbuzi wa Equation ya Linear katika Vigezo viwili

Katika mazoezi yafuatayo, tafuta ufumbuzi wa tatu kwa kila equation linear.

x + y = 3
x + y = -4
y = 3x + 1
y = - x - 1

11.2 - Mchoro wa Mstari wa Mstari

Tambua Uhusiano Kati ya Ufumbuzi wa Equation na Grafu yake

Katika mazoezi yafuatayo, kwa kila jozi iliyoamriwa, chagua (a) ikiwa jozi iliyoamriwa ni suluhisho la equation. (b) ikiwa hatua iko kwenye mstari.

y = - x + 4
1. (0, 4)
2. (-1, 3)
3. (2, 2)
4. (-2, 6)

$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 4” na “jozi iliyoamriwa 4, 0”.$

y = $\dfrac{2}{3}$ x - 1
1. (0, -1)
2. (3, 1)
3. (1-3, -3)
4. (6, 4)

$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, -1” na “jozi iliyoamriwa 3, 1”.$

Grafu Ulinganisho wa Mstari na Pointi za Kupanga

Katika mazoezi yafuatayo, grafu kwa pointi za kupanga.

y = 4x - 3
y = -3x
2x + y = 7

Grafu mistari ya wima na ya usawa

Katika mazoezi yafuatayo, graph mistari ya wima au ya usawa.

y = -2
x = 3

11.3 - Graphing na Intercepts

Tambua Intercepts kwenye Grafu

Katika mazoezi yafuatayo, tafuta x- na y-intercepts.

$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 4” na “jozi iliyoamriwa -4, 0”.$
$Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -1 hadi 6. Mhimili wa y huendesha kutoka -4 hadi 2. Mstari unapita kupitia pointi “jozi iliyoamriwa 5, 1” na “jozi iliyoamriwa 0, -3”.$

Kupata Intercepts kutoka Equation ya Line

Katika mazoezi yafuatayo, pata vipindi.

x + y = 5
x - y = -1
y = $\dfrac{3}{4}$ x - 12
y = 3x

Grafu Mstari Kutumia Intercepts

Katika mazoezi yafuatayo, grafu kwa kutumia intercepts.

-x + 3y = 3
x + y = -2

Chagua Njia rahisi zaidi ya Grafu ya Mstari

Katika mazoezi yafuatayo, tambua njia rahisi zaidi ya kuchora kila mstari.

x = 5
y = -3
2x + y = 5
x - y = 2
y = $\dfrac{1}{2}$ x + 2
y = $\dfrac{3}{4}$ x - 1

11.4 - Kuelewa Mteremko wa Line

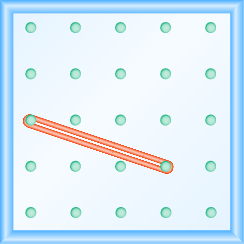
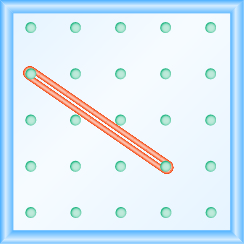
Tumia Geoboards kwa Mfano wa Mfano

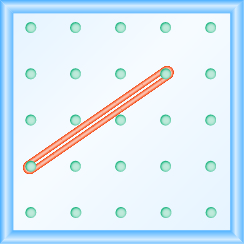
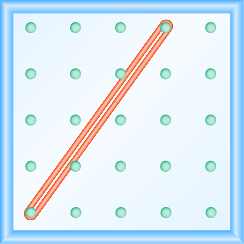
Katika mazoezi yafuatayo, tafuta mteremko unaoelekezwa kwenye kila geoboard.

$Takwimu inaonyesha gridi ya dots sawasawa spaced. Kuna safu 5 na nguzo 5. Kuna kitanzi cha mtindo wa bendi ya mpira kinachounganisha hatua katika safu ya 1 mstari wa 4 na uhakika katika safu ya 4 mstari wa 2.$
$Takwimu inaonyesha gridi ya dots sawasawa spaced. Kuna safu 5 na nguzo 5. Kuna kitanzi cha mtindo wa bendi ya mpira kinachounganisha hatua katika safu ya 1 mstari wa 5 na uhakika katika safu ya 4 mstari 1.$
$Takwimu inaonyesha gridi ya dots sawasawa spaced. Kuna safu 5 na nguzo 5. Kuna kitanzi cha mtindo wa bendi ya mpira kinachounganisha hatua katika safu ya 1 mstari 3 na hatua katika safu ya 4 mstari 4.$
$Takwimu inaonyesha gridi ya dots sawasawa spaced. Kuna safu 5 na nguzo 5. Kuna kitanzi cha mtindo wa bendi ya mpira kinachounganisha hatua katika safu ya 1 mstari 2 na hatua katika safu ya 4 mstari 4.$

Katika mazoezi yafuatayo, mfano kila mteremko. Chora picha ili kuonyesha matokeo yako.

$\dfrac{1}{3}$
$\dfrac{3}{2}$
$− \dfrac{2}{3}$
$− \dfrac{1}{2}$

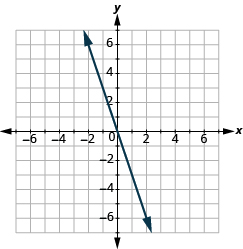
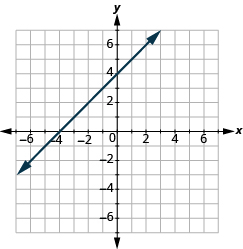
Pata mteremko wa Mstari kutoka kwenye Grafu yake

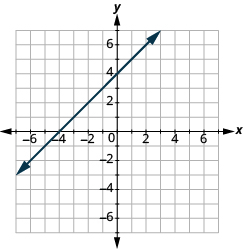
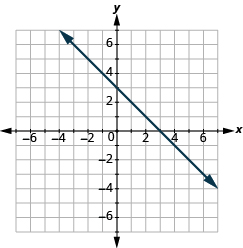
Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari umeonyeshwa.

$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 0” na “jozi iliyoamriwa 2, -6".$
$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 4” na “jozi iliyoamriwa -4, 0”.$
$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa -4, -4” na “jozi iliyoamuru 5, -1”.$
$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa -3, 6" na “jozi iliyoamuru 5, 2".$

Pata mteremko wa Mistari ya Ulalo na Wima

Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari.

y = 2
x = 5
x = -3
y = -1

Tumia Mfumo wa Slope ili kupata mteremko wa Mstari kati ya Pointi mbili

Katika mazoezi yafuatayo, tumia fomu ya mteremko ili kupata mteremko wa mstari kati ya kila jozi ya pointi.

(2, 1), (4, 5)
(-1, -1), (0, -5)
(3, 5), (4, -1)
(-5, -2), (3, 2)

Grafu Mstari Kutolewa Point na Slope

Katika mazoezi yafuatayo, graph mstari uliopewa uhakika na mteremko.

(2, -1); m = $\dfrac{5}{2}$
(1-3, 4); m = $− \dfrac{1}{3}$

Kutatua Maombi ya mteremko

Katika zoezi zifuatazo, tatua maombi ya mteremko.

Paa imeongezeka miguu 10 na kukimbia miguu 15. Mteremko wake ni nini?

MTIHANI WA MAZOEZI

Plot na studio pointi hizi:
1. (2, 5)
2. (-1, 1-3)
3. (-4, 0)
4. (3, -5)
5. (-1, 1)
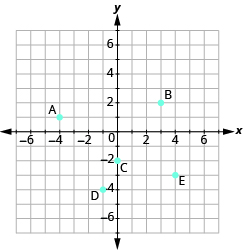
Jina jozi iliyoamriwa kwa kila hatua iliyoonyeshwa.

$Grafu inaonyesha ndege ya kuratibu x y. Axes hupanua kutoka -7 hadi 7. A imepangwa saa -4, 1, B saa 3, 2, C saa 0, -2, D saa -1, -4, na E saa 4, -3.$

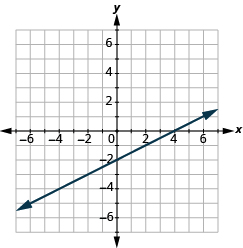
Pata x-intercept na y-intercept kwenye mstari ulioonyeshwa.

$Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -7 hadi 7. Mhimili wa y huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 4, 0” na “jozi iliyoamriwa 0, -2”.$

Pata x-intercept na y-intercept ya equation 3x - y = 6.
Je, (1, 3) ufumbuzi wa equation x + 4y = 12? Unajuaje?
Jaza meza ili kupata ufumbuzi wa nne kwa equation y = - x + 1.

x	y	(x, y)
0
1
3
-2

Jaza meza ili kupata ufumbuzi wa tatu kwa equation 4x + y = 8.

x	y	(x, y)
0
	0
3

Katika mazoezi yafuatayo, pata ufumbuzi wa tatu kwa kila equation na kisha graph kila mstari.

y = -3x
2x + 3y = -6

Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari.

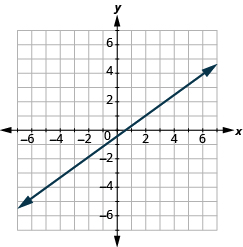
$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. Mhimili wa y huendesha kutoka -5 hadi -4. Mstari unapita kupitia pointi “jozi iliyoamriwa 6, 4" na “jozi iliyoamriwa 0, -3”.$
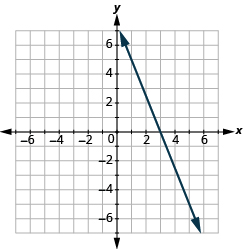
$Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 3, 0” na “jozi iliyoamriwa 1, 5".$
Tumia fomu ya mteremko ili kupata mteremko wa mstari kati ya (0, -4) na (5, 2).
Pata mteremko wa mstari y = 2.
Grafu mstari unaopita (1, 1) na mteremko m = $\dfrac{3}{2}$ .
Njia ya baiskeli inapanda miguu 20 kwa miguu 1,000 ya umbali wa usawa. Je, ni mteremko wa njia gani?

Wachangiaji na sifa

Template:ContribOpenStaxPreAlgebra