Skip to main content
Global

11.8: Kuelewa mteremko wa Line (Sehemu ya 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    173388

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Grafu Mstari Kutolewa Point na Slope

    Katika sura hii, sisi graphed mistari kwa pointi njama, kwa kutumia intercepts, na kwa kutambua mistari usawa na wima.

    Njia nyingine tunaweza kutumia kwa mistari ya grafu ni njia ya mteremko wa uhakika. Wakati mwingine, tutapewa hatua moja na mteremko wa mstari, badala ya usawa wake. Wakati hii itatokea, tunatumia ufafanuzi wa mteremko kuteka grafu ya mstari.

    Mfano\(\PageIndex{11}\):

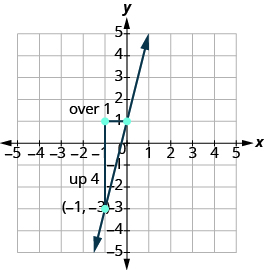
    Grafu mstari unaopita kupitia hatua (1, -1) ambao mteremko wake ni m =\(\dfrac{3}{4}\).

    Suluhisho

    Panda hatua iliyotolewa, (1, -1).

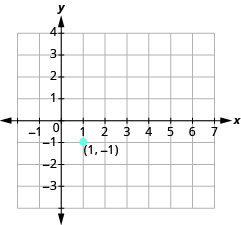
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -1 hadi 7. Mhimili wa y huendesha kutoka -3 hadi 4. Hatua iliyoandikwa hutolewa kwenye “jozi iliyoamriwa 1, -1”.

    Tumia formula ya mteremko m =\(\dfrac{rise}{run}\) kutambua kupanda na kukimbia.

    \[\begin{split} m &= \dfrac{3}{4} \\ \dfrac{rise}{run} &= \dfrac{3}{4} \\ rise &= 3 \\ run &= 4 \end{split}\]

    Kuanzia wakati tulipanga njama, uhesabu kupanda na kukimbia ili alama ya pili. Tunahesabu 3 vitengo juu na 4 vitengo haki.

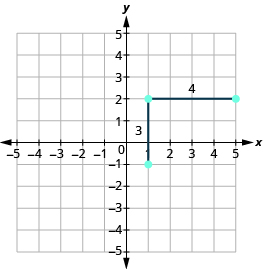
    Grafu inaonyesha ndege ya kuratibu x y. Axes zote mbili zinaendesha kutoka -5 hadi 5. Makundi mawili ya mstari hutolewa. Sehemu ya mstari wa wima inaunganisha pointi “jozi iliyoamriwa 1, -1” na “jozi ya utaratibu “1, 2". Imeandikwa “3". Sehemu ya mstari wa usawa huanza juu ya sehemu ya mstari wa wima na huenda kwa haki, kuunganisha pointi “jozi iliyoamriwa 1, 2" na “jozi iliyoamriwa 5, 2”. Imeandikwa “4".

    Kisha sisi huunganisha pointi kwa mstari na kuteka mishale mwishoni ili kuonyesha inaendelea.

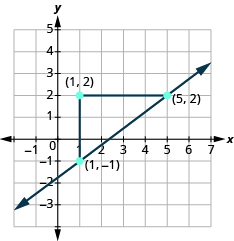
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -3 hadi 5. Mhimili wa y huendesha kutoka -1 hadi 7. Vipengele viwili visivyochaguliwa vinatolewa kwenye “jozi iliyoamriwa 1, -1” na “jozi iliyoamriwa 5, 2". Mstari unapita kupitia pointi. Makundi mawili ya mstari huunda pembetatu na mstari. Mstari wa wima unaunganisha “jozi iliyoamriwa 1, -1” na “jozi iliyoamriwa 1, 2". Sehemu ya mstari wa usawa inaunganisha “jozi iliyoamriwa 1, 2" na “jozi iliyoamriwa 5, 2".

    Tunaweza kuangalia mstari wetu kwa kuanzia wakati wowote na kuhesabu hadi 3 na kulia 4. Tunapaswa kupata hatua nyingine kwenye mstari.

    Zoezi\(\PageIndex{21}\):

    Grafu mstari unaopita kupitia hatua na mteremko uliopewa:

    (2, -1), m =\(\dfrac{4}{3}\)

    Jibu

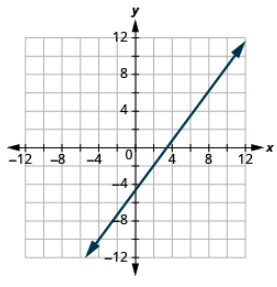
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -12 hadi 12. Mhimili wa y huendesha kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa -2, 3" na “jozi iliyoamriwa 8, 6".

    Zoezi\(\PageIndex{22}\):

    Grafu mstari unaopita kupitia hatua na mteremko uliopewa:

    (-2, 3), m =\(\dfrac{1}{4}\)

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -12 hadi 12. Mhimili wa y huendesha kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa -2, 3" na “jozi iliyoamriwa 2, 4".

    JINSI YA: GRAFU MSTARI ULIOPEWA UHAKIKA NA MTEREMKO

    Hatua ya 1. Panda hatua iliyotolewa.

    Hatua ya 2. Tumia formula ya mteremko kutambua kupanda na kukimbia.

    Hatua ya 3. Kuanzia kwenye hatua iliyotolewa, uhesabu kupanda na kukimbia ili alama ya pili.

    Hatua ya 4. Unganisha pointi kwa mstari.

    Mfano\(\PageIndex{12}\):

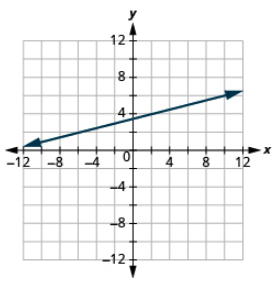
    Grafu mstari na y -intercept (0, 2) na mteremko m =\(− \dfrac{2}{3}\).

    Suluhisho

    Panda hatua iliyotolewa, y -intercept (0, 2).

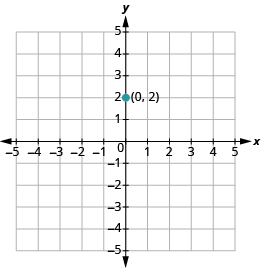
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -1 hadi 4. Mhimili wa y huendesha kutoka -1 hadi 3. Hatua “jozi iliyoamriwa 0, 2” imeandikwa.

    Tumia formula ya mteremko m = kupanda kukimbia kutambua kupanda na kukimbia.

    \[\begin{split} m &= − \dfrac{2}{3} \\ \dfrac{rise}{run} &= \dfrac{−2}{3} \\ rise &= –2 \\ run &= 3 \end{split}\]

    Kuanzia saa (0, 2), uhesabu kupanda na kukimbia na uangalie hatua ya pili.

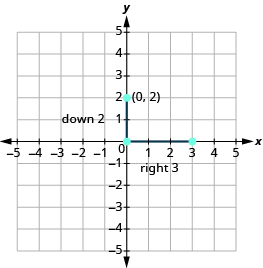
    Grafu inaonyesha ndege ya kuratibu x y. Axes zote mbili zinaendesha kutoka -5 hadi 5. Sehemu ya mstari wa wima huunganisha pointi kwenye “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa 0, 0" na inaitwa “chini 2". Sehemu ya mstari wa usawa inaunganisha “jozi iliyoamriwa 0, 0” na “jozi iliyoamriwa 0, 3" na imeandikwa “haki 3".

    Unganisha pointi kwa mstari.

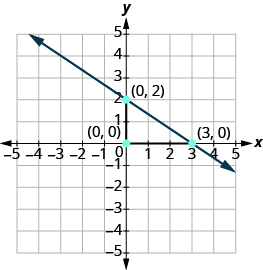
    Grafu inaonyesha ndege ya kuratibu x y. Axes zote mbili zinaendesha kutoka -5 hadi 5. Vipengele viwili vilivyoandikwa vinatolewa kwenye “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa 3, 0". Mstari unapita kupitia pointi. Makundi mawili ya mstari huunda pembetatu na mstari. Mstari wa wima unaunganisha “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa 0, 0”. Sehemu ya mstari wa usawa inaunganisha “jozi iliyoamriwa 0, 0" na “jozi iliyoamriwa 3, 0”.

    Zoezi\(\PageIndex{23}\):

    Graph mstari na intercept iliyotolewa na mteremko:

    y-kukatiza 4, m =\(− \dfrac{5}{2}\)

    Jibu

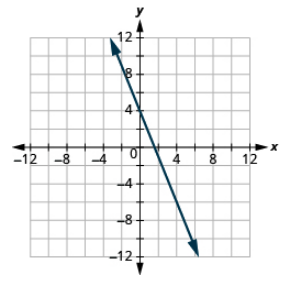
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -12 hadi 12. Mhimili wa y huendesha kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 4” na “jozi iliyoamriwa 4, -6".

    Zoezi\(\PageIndex{24}\):

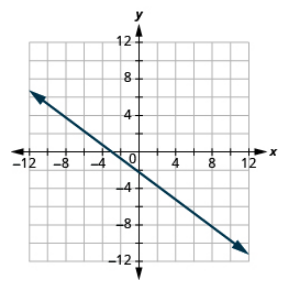
    Graph mstari na intercept iliyotolewa na mteremko:

    x-intercept -3, m =\(− \dfrac{3}{4}\)

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -12 hadi 12. Mhimili wa y huendesha kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa -3, 0” na “jozi iliyoamriwa 8, -8".

    Mfano\(\PageIndex{13}\):

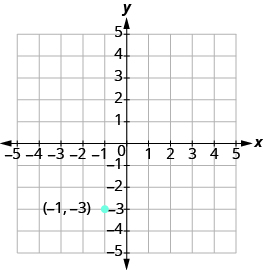
    Grafu mstari unaopita kupitia hatua (-1, 1-3) ambao mteremko wake ni m = 4.

    Suluhisho

    Panda hatua iliyotolewa.

    Grafu inaonyesha ndege ya kuratibu x y. Axes zote mbili zinaendesha kutoka -5 hadi 5. Hatua “jozi iliyoamriwa -1, -3” imeandikwa.

    Tambua kupanda na kukimbia. $$m = 4\ tag {11.4.44} $$
    Andika 4 kama sehemu. $$\ dfrac {kupanda} {kukimbia} =\ dfrac {4} {1}\ tag {11.4.45} $$
      kupanda = 4, kukimbia = 1

    Hesabu kupanda na kukimbia.

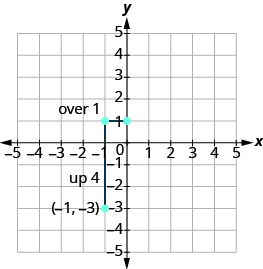
    Grafu inaonyesha ndege ya kuratibu x y. Axes zote mbili zinaendesha kutoka -5 hadi 5. Mhimili wa y huendesha kutoka -4 hadi 2. Sehemu ya mstari wa wima huunganisha pointi kwenye “jozi iliyoamriwa -1, -3” na “jozi iliyoamriwa -1, 1” na inaitwa “up 4". Sehemu ya mstari ya usawa inaunganisha “jozi iliyoamriwa -1, 1” na “jozi iliyoamriwa 0, 1” na imeandikwa “juu ya 1”.

    Andika alama ya pili. Unganisha pointi mbili na mstari.

    Grafu inaonyesha ndege ya kuratibu x y. Axes zote mbili zinaendesha kutoka -5 hadi 5. Vipengele viwili vilivyoandikwa vinatolewa kwenye “jozi iliyoamriwa -1, -3” na “jozi iliyoamriwa -1, 1”. Mstari unapita kupitia pointi. Makundi mawili ya mstari huunda pembetatu na mstari. Mstari wa wima unaunganisha “jozi iliyoamriwa -1, -3” na “jozi iliyoamriwa -1, 1”. Ni kinachoitwa “up 4” usawa line sehemu unajumuisha “kuamuru jozi -1, 1” na “kuamuru jozi 0, 1”. Ni kinachoitwa “zaidi ya 1”

    Zoezi\(\PageIndex{25}\):

    Grafu mstari na intercept iliyotolewa na mteremko: (-1, 1), m = 3.

    Jibu

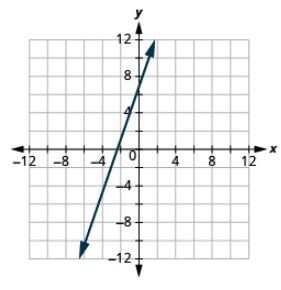
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -7 hadi 7. Mhimili wa y huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa -2, 1” na “jozi iliyoamriwa 0, 7”.

    Zoezi\(\PageIndex{26}\):

    Grafu mstari na intercept iliyotolewa na mteremko: (4, -1), m = -1.

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -7 hadi 7. Mhimili wa y huendesha kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 6" na “jozi iliyoamriwa 0, 3".

    Kutatua Maombi ya mteremko

    Mwanzoni mwa sehemu hii, tulisema kuna maombi mengi ya mteremko katika ulimwengu wa kweli. Hebu tuangalie wachache sasa.

    Mfano\(\PageIndex{14}\):

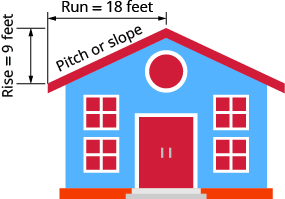
    Upeo wa paa la jengo ni mteremko wa paa. Kujua lami ni muhimu katika hali ya hewa ambapo kuna theluji nzito. Ikiwa paa ni gorofa mno, uzito wa theluji unaweza kusababisha kuanguka. Je! Mteremko wa paa umeonyeshwa nini?

    Takwimu hii inaonyesha nyumba yenye paa la mteremko. Paa juu ya nusu moja ya jengo inaitwa “lami ya paa”. Kuna sehemu ya mstari na mishale kila mwisho kupima urefu wa wima wa paa na inaitwa “kupanda = futi 9". Kuna sehemu ya mstari na mishale kila mwisho kupima urefu usio na usawa wa mizizi na inaitwa “kukimbia = futi 18".

    Suluhisho

    Tumia formula ya mteremko. $$m =\ dfrac {kupanda} {kukimbia}\ tag {11.4.46} $$
    Badilisha maadili ya kupanda na kukimbia. $$m =\ dfrac {9\; ft} {18\; ft}\ tag {11.4.47} $$
    Kurahisisha. $$m =\ dfrac {1} {2}\ tag {11.4.48} $$
      Mteremko wa paa ni\(\dfrac{1}{2}\).
    Zoezi\(\PageIndex{27}\):

    Kupata mteremko kutokana kupanda na kukimbia: paa na kupanda = 14 na kukimbia = 24.

    Jibu

    \(\frac{7}{12}\)

    Zoezi\(\PageIndex{28}\):

    Kupata mteremko kutokana kupanda na kukimbia: paa na kupanda = 15 na kukimbia = 36.

    Jibu

    \(\frac{5}{12}\)

    Je! Umewahi kufikiri juu ya mabomba ya maji taka yanayotoka nyumbani kwako hadi mitaani? Mteremko wao ni jambo muhimu katika jinsi wanavyochukua taka mbali na nyumba yako.

    Mfano\(\PageIndex{15}\):

    Mabomba ya maji taka yanapaswa kuteremka\(\dfrac{1}{4}\) inchi kwa mguu ili kukimbia vizuri. Je, ni mteremko unaohitajika?

    Takwimu hii inaonyesha pembetatu sahihi. Mguu mfupi ni wima na umeandikwa “1 juu ya inchi 4". Mguu mrefu ulioitwa “mguu 1".

    Suluhisho

    Tumia formula ya mteremko. $$m =\ dfrac {kupanda} {kukimbia} =\ dfrac {-\ dfrac {1} {4}\; katika.} {1\; ft}\ tag {11.4.49} $$
    Badilisha mguu 1 hadi inchi 12. $$m =\ dfrac {-\ dfrac {1} {4}\; in.} {12\; katika}\ tag {11.4.50} $$
    Kurahisisha. $$m = -\ dfrac {1} {48}\ tag {11.4.51} $$
      Mteremko wa bomba ni\(− \dfrac{1}{48}\).
    Zoezi\(\PageIndex{29}\):

    Pata mteremko wa bomba: mteremko wa bomba chini\(\dfrac{1}{3}\) inchi kwa mguu.

    Jibu

    \(-\frac{1}{36}\)

    Zoezi\(\PageIndex{30}\):

    Pata mteremko wa bomba: mteremko wa bomba chini\(\dfrac{3}{4}\) inchi kwa kila yadi.

    Jibu

    \(-\frac{1}{48}\)

    PATA RASILIMALI ZA ZIADA

    Tambua mteremko Mzuri kutoka kwenye Grafu

    Kuamua mteremko mbaya kutoka Grafu

    Tambua Mteremko kutoka kwa Pointi mbili

    Mazoezi hufanya kamili

    Tumia Geoboards kwa Mfano wa Mfano

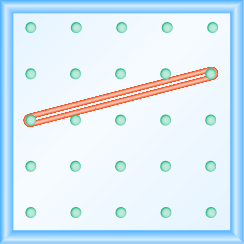
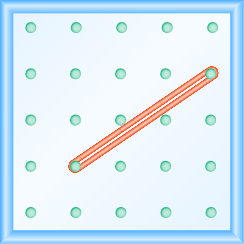
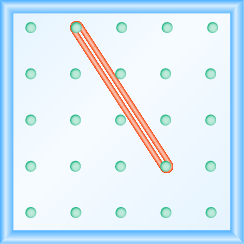
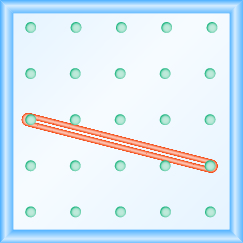
    Katika mazoezi yafuatayo, tafuta mteremko unaoelekezwa kwenye kila geoboard.

    1. Takwimu inaonyesha gridi ya dots sawasawa spaced. Kuna safu 5 na nguzo 5. Kuna kitanzi cha mtindo wa bendi ya mpira kinachounganisha hatua katika safu ya 1 mstari wa 3 na uhakika katika safu ya 5 mstari wa 2.
    2. Takwimu inaonyesha gridi ya dots sawasawa spaced. Kuna safu 5 na nguzo 5. Kuna kitanzi cha mtindo wa bendi ya mpira kinachounganisha hatua katika safu ya 2 mstari 4 na hatua katika safu ya 5 mstari wa 2.
    3. Takwimu inaonyesha gridi ya dots sawasawa spaced. Kuna safu 5 na nguzo 5. Kuna kitanzi cha mtindo wa bendi ya mpira kinachounganisha hatua katika safu ya 2 mstari 1 na hatua katika safu ya 4 mstari 4.
    4. Takwimu inaonyesha gridi ya dots sawasawa spaced. Kuna safu 5 na nguzo 5. Kuna kitanzi cha mtindo wa bendi ya mpira kinachounganisha hatua katika safu ya 2 mstari 1 na hatua katika safu ya 4 mstari 4.

    Katika mazoezi yafuatayo, mfano kila mteremko. Chora picha ili kuonyesha matokeo yako.

    1. \(\dfrac{2}{3}\)
    2. \(\dfrac{3}{4}\)
    3. \(\dfrac{1}{4}\)
    4. \(\dfrac{4}{3}\)
    5. \(- \dfrac{1}{2}\)
    6. \(- \dfrac{3}{4}\)
    7. \(- \dfrac{2}{3}\)
    8. \(- \dfrac{3}{2}\)

    Pata mteremko wa Mstari kutoka kwenye Grafu yake

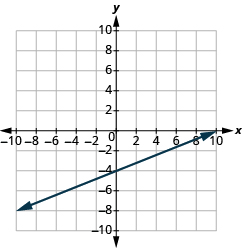
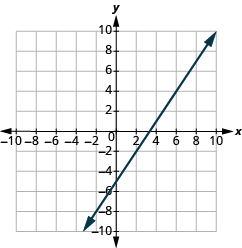
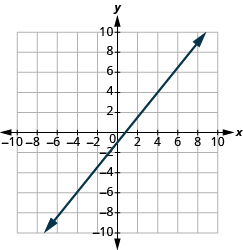
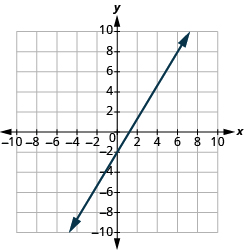
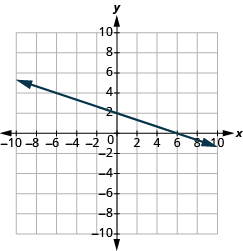
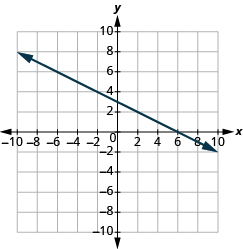
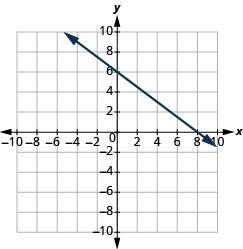
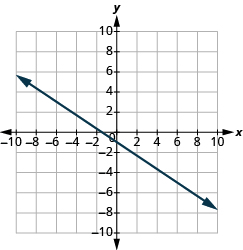
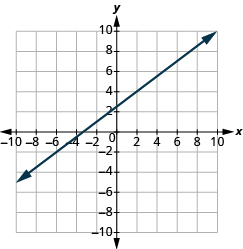
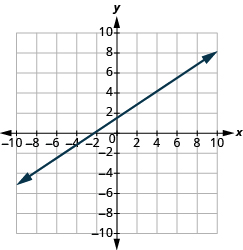
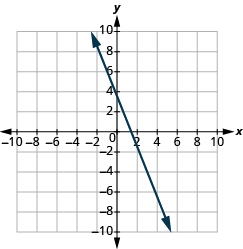
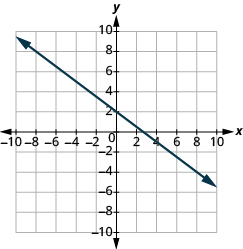
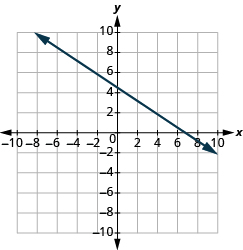
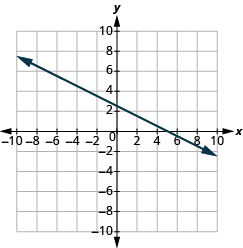
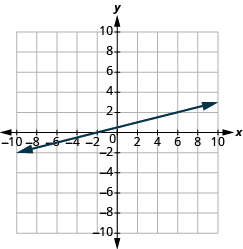
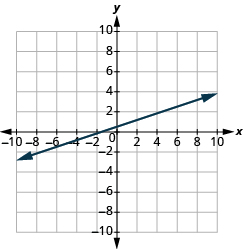
    Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari umeonyeshwa.

    1. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mhimili wa y huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, -4” na “jozi iliyoamriwa 10, 0”.
    2. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mhimili wa y huendesha kutoka -10 hadi 10. mstari hupita kupitia pointi “kuamuru jozi 0, -5" na “kuamuru jozi 3, 0”.
    3. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -12 hadi 12. Mhimili wa y huendesha kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, -1” na “jozi iliyoamriwa 1, 0”.
    4. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mhimili wa y huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 3" na “jozi iliyoamriwa 6, 0”.
    5. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mhimili wa y huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa 6, 0”.
    6. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mhimili wa y huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa 6, 0”.
    7. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mhimili wa y huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 6" na “jozi iliyoamriwa 8, 0”.
    8. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mhimili wa y huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa -1, 0” na “jozi iliyoamriwa 0, -1”.
    9. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mhimili wa y huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa -4, 0” na “jozi iliyoamriwa -4, 6".
    10. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mhimili wa y huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa -2, 0” na “jozi iliyoamriwa 4, 4".
    11. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 4” na “jozi iliyoamriwa 4, -6".
    12. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 4” na “jozi iliyoamriwa 4, -6".
    13. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 1, 4" na “jozi iliyoamriwa 7, 0”.
    14. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 3" na “jozi iliyoamriwa 7, 0”.
    15. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 2, 0” na “jozi iliyoamriwa 10, 4".
    16. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 6, 2" na “jozi iliyoamriwa 0, -3”.

    Pata mteremko wa Mistari ya Ulalo na Wima

    Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari.

    1. y = 3
    2. y = 1
    3. x = 4
    4. x = 2
    5. y = -2
    6. y = -3
    7. x = -5
    8. x = -4

    Tumia Mfumo wa Slope ili kupata mteremko wa Mstari kati ya Pointi mbili

    Katika mazoezi yafuatayo, tumia fomu ya mteremko ili kupata mteremko wa mstari kati ya kila jozi ya pointi.

    1. (1, 4), (3, 9)
    2. (2, 3), (5, 7)
    3. (0, 3), (4, 6)
    4. (0, 1), (5, 4)
    5. (2, 5), (4, 0)
    6. (3, 6), (8, 0)
    7. (1-3, 3), (2, -5)
    8. (-1, 4), (3, -1)
    9. (-1, -2), (2, 5)
    10. (-1, -1), (6, 5)
    11. (4, -5), (1, -1)
    12. (3, -6), (2, -2)

    Grafu Mstari Kutolewa Point na Slope

    Katika mazoezi yafuatayo, graph mstari uliopewa uhakika na mteremko.

    1. (1, ¯ 2); m =\(\dfrac{3}{4}\)
    2. (1, -1); m =\(\dfrac{1}{2}\)
    3. (2, 5); m =\(− \dfrac{1}{3}\)
    4. (1, 4); m =\(− \dfrac{1}{2}\)
    5. (1-3, 4); m =\(− \dfrac{3}{2}\)
    6. (-2, 5); m =\(− \dfrac{5}{4}\)
    7. . (-1, -4); m =\(\dfrac{4}{3}\)
    8. (-3, -5); m =\(\dfrac{3}{2}\)
    9. (0, 3); m =\(− \dfrac{2}{5}\)
    10. (0, 5); m =\(− \dfrac{4}{3}\)
    11. (-2, 0); m =\(−\dfrac{3}{4}\)
    12. (-1, 0); m =\(\dfrac{1}{5}\)
    13. (1-3, 3); m = 2
    14. (-4, 2); m = 4
    15. (1, 5); m = -3
    16. (2, 3); m = -1

    Kutatua Maombi ya mteremko

    Katika mazoezi yafuatayo, tatua maombi haya ya mteremko.

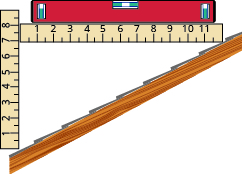
    1. Mteremko wa paa Njia rahisi ya kuamua mteremko ni kuchukua kiwango cha inchi 12 na kuiweka kwenye mwisho mmoja juu ya uso wa paa. Kisha kuchukua kipimo cha mkanda au mtawala, na kupima kutoka mwisho mwingine wa ngazi hadi kwenye uso wa paa. Unaweza kutumia vipimo hivi kuhesabu mteremko wa paa. Je, ni mteremko wa paa katika picha hii?

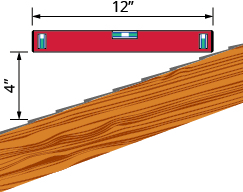
    Takwimu inaonyesha bodi ya kuni kwenye diagonal inayowakilisha kipande cha mtazamo wa upande wa paa iliyopigwa. Sehemu ya mstari wa wima na mishale kwenye ncha zote mbili inachukua mabadiliko ya wima kwa urefu wa paa na inaitwa “inchi 4". Chombo cha ngazi iko katika nafasi ya usawa juu ya ubao na juu yake ni sehemu ya mstari na mishale kwenye ncha zote mbili zilizoitwa “inchi 12".

    1. Je! Mteremko wa paa umeonyeshwa nini?

    Takwimu inaonyesha kipande cha mtazamo wa upande wa diagonal wa paa iliyopigwa. Mtawala katika nafasi ya wima ni chini ya sehemu ya paa na inaonyesha maandiko ya kitengo 1 hadi 8 na huongeza kitengo kimoja zaidi. Mtawala wa pili anaanza kwenye lebo ya “7" ya mtawala wa wima na huendelea kwa usawa mpaka inapiga paa inayoinuka. Mtawala wa usawa ana maandiko ya kitengo 1 hadi 11 na huongeza kitengo kimoja zaidi.

    1. Daraja la barabara barabara ya ndani ina daraja la 6%. Daraja la barabara ni mteremko wake ulioonyeshwa kama asilimia.
      1. Pata mteremko wa barabara kama sehemu na kisha uwezesha sehemu.
      2. Nini kupanda na kukimbia bila kutafakari mteremko huu au daraja?
    2. Highway daraja barabara ya ndani kuongezeka 2 miguu kwa kila 50 miguu ya barabara kuu.
      1. Je, ni mteremko wa barabara kuu?
      2. Daraja la barabara kuu ni mteremko wake ulioonyeshwa kama asilimia. Je! Ni daraja gani la barabara kuu hii?

    kila siku Math

    1. Njia ya magurudumu Sheria za ramps za magurudumu zinahitaji upeo 1 inch kupanda kwa 12 inch kukimbia.
      1. Je, barabara lazima iwe kwa muda gani ili kuzingatia kupanda kwa inchi 24 hadi mlango?
      2. Chora mfano wa barabara hii.
    2. Njia ya magurudumu Kuongezeka kwa inchi 1 kwa kukimbia kwa inchi 16-inch inafanya iwe rahisi kwa mpanda farasi wa magurudumu kupaa barabara.
      1. Je, barabara lazima iwe kwa muda gani ili kuhudhuria kupanda kwa inchi 24 hadi mlango?
      2. Chora mfano wa barabara hii.

    Mazoezi ya kuandika

    1. Ishara ya mteremko inakuambia nini kuhusu mstari?
    2. Je, grafu ya mstari na mteremko m =\(\dfrac{1}{2}\) hutofautiana na grafu ya mstari na mteremko m = 2?
    3. Kwa nini mteremko wa mstari wa wima haujafafanuliwa?
    4. Eleza jinsi unaweza kuchora mstari uliopewa uhakika na mteremko wake.

    Self Check

    (a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

    CNX_BMath_Figure_AppB_069.jpg

    (b) Kwa kiwango cha 1—10, ungewezaje kupima ujuzi wako wa sehemu hii kwa kuzingatia majibu yako kwenye orodha? Unawezaje kuboresha hii?

    Wachangiaji na Mashtaka