Skip to main content
Global

11.6: Graphing na Intercepts (Sehemu ya 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    173384

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Chagua Njia rahisi zaidi ya Grafu ya Mstari

    Wakati tunaweza graph equation yoyote linear kwa pointi njama, inaweza daima kuwa njia rahisi zaidi. Jedwali hili linaonyesha sita ya milinganyo tumekuwa graphed katika sura hii, na mbinu sisi kutumika graph yao.

    Mlinganyo Mbinu
    #1 y = 2x + 1 Kupanga pointi
    #2 y =\(\dfrac{1}{2}\) x + 3 Kupanga pointi
    #3 x = -7 Mstari wa wima
    #4 y = 4 Mstari wa usawa
    #5 2x + y = 6 Inakataza
    #6 4x - 3y = 12 Inakataza

    Ni nini kuhusu fomu ya equation ambayo inaweza kutusaidia kuchagua njia rahisi zaidi ya kuchora mstari wake?

    Angalia kwamba katika equations #1 na #2, y ni pekee kwa upande mmoja wa equation, na mgawo wake ni 1. Tulipata pointi kwa kubadilisha maadili kwa x upande wa kulia wa equation na kisha kurahisisha kupata sambamba y- maadili.

    Ulinganifu #3 na #4 kila mmoja variable moja tu. Kumbuka, katika aina hii ya equation thamani ya variable kwamba moja ni mara kwa mara; haina hutegemea thamani ya variable nyingine. Ulinganisho wa fomu hii una grafu ambazo ni mistari ya wima au ya usawa.

    Katika equations #5 na #6, wote x na y ni upande mmoja wa equation. Hizi milinganyo miwili ni ya fomu Ax + By = C. Tulibadilisha y = 0 na x = 0 ili kupata x- na y- intercepts, na kisha kupatikana hatua ya tatu kwa kuchagua thamani kwa x au y.

    Hii inasababisha mkakati wafuatayo wa kuchagua njia rahisi zaidi ya kuchora mstari.

    JINSI YA: CHAGUA NJIA RAHISI ZAIDI YA GRAPH MSTARI

    Hatua ya 1. Kama equation ina variable moja tu. Ni mstari wa wima au usawa.

    • x = a ni mstari wima kupita kwa njia ya x-mhimili katika.
    • y = b ni mstari usio na usawa unaopita kupitia mhimili wa y saa b.

    Hatua ya 2. Kama y ni pekee upande mmoja wa equation. Grafu kwa pointi za kupanga njama.

    • Chagua maadili yoyote matatu kwa x na kisha kutatua kwa sambamba y- maadili.

    Hatua ya 3. Kama equation ni ya fomu Ax + By = C, kupata intercepts.

    • Kupata x- na y- intercepts na kisha hatua ya tatu.
    Mfano\(\PageIndex{7}\):

    Tambua njia rahisi zaidi ya grafu kila mstari: (a) y = -3 (b) 4x-6y = 12 (c) x = 2 (d) y = 2 5 x-1

    Suluhisho

    (a) y = -3

    Equation hii ina variable moja tu, y. grafu yake ni mstari usawa kuvuka y mhimili katika -3.

    (b) 4x-6y = 12

    Equation hii ni ya fomu Ax + By = C. kupata intercepts na hatua moja zaidi.

    (c) x = 2

    Kuna variable moja tu, x. grafu ni mstari wima kuvuka x-axis saa 2.

    (d) y =\(\dfrac{2}{5}\) x-1

    Kwa kuwa y imetengwa upande wa kushoto wa equation, itakuwa rahisi kupiga mstari huu kwa kupanga njama tatu.

    Zoezi\(\PageIndex{7A}\):

    Tambua njia rahisi zaidi ya grafu kila mstari: (a) 3x + 2y = 12 (b) y = 4 (c) y =\(\dfrac{1}{5}\) x-4 (d) x = -7

    Jibu

    ingilia kati

    Jibu b

    mstari usio na usawa

    Jibu c

    pointi za kupanga njama

    Jibu d

    mstari wa wima

    Zoezi\(\PageIndex{7B}\):

    Tambua njia rahisi zaidi ya grafu kila mstari: (a) x = 6 (b) y =\(− \dfrac{3}{4}\) x + 1 (c) y = -8 (d) 4x-3y = -1

    Jibu

    mstari wa wima

    Jibu b

    pointi za kupanga njama

    Jibu c

    mstari usio na usawa

    Jibu d

    ingilia kati

    PATA RASILIMALI ZA ZIADA

    Grafu kwa Kupata Intercepts

    Tumia Intercepts kwa Grafu

    Hali ya Intercepts kutoka Grafu

    Mazoezi hufanya kamili

    Tambua Intercepts kwenye Grafu

    Katika mazoezi yafuatayo, tafuta x- na y- intercepts.

    1. Grafu inaonyesha ndege ya kuratibu x y. Axes huendesha kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 3" na “jozi iliyoamriwa 3, 0”.
    2. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa 2, 0”.
    3. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -10 hadi 10. mstari hupita kupitia pointi “kuamuru jozi 0, -5" na “kuamuru jozi 5, 0”.
    4. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, -1” na “jozi iliyoamriwa 1, 0”.
    5. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, -2” na “jozi iliyoamriwa -2, 0”.
    6. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, -3” na “jozi iliyoamriwa -3, 0”.
    7. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 1” na “jozi iliyoamriwa -1, 0”.
    8. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -10 hadi 10. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 5” na “jozi iliyoamriwa -5, 0”.
    9. Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 0” na “jozi iliyoamriwa 4, 2".

    Kupata x na y Intercepts kutoka Equation ya Line

    Katika mazoezi yafuatayo, pata vipindi.

    1. x + y = 4
    2. x + y = 3
    3. x + y = -2
    4. x + y = -5
    5. x - y = 5
    6. x - y = 1
    7. x - y = -3
    8. x - y = -4
    9. x + 2y = 8
    10. x + 2y = 10
    11. 3x + y = 6
    12. 3x + y = 9
    13. x-3y = 12
    14. x-2y = 8
    15. 4x - y = 8
    16. 5x - y = 5
    17. 2x + 5y = 10
    18. 2x + 3y = 6
    19. 3x-2y = 12
    20. 3x-5y = 30
    21. y =\(\dfrac{1}{3}\) x-1
    22. y =\(\dfrac{1}{4}\) x-1
    23. y =\(\dfrac{1}{5}\) x + 2
    24. y =\(\dfrac{1}{3}\) x + 4
    25. y = 3x
    26. y = -2x
    27. y = -4x
    28. y = 5x

    Grafu Mstari Kutumia Intercepts

    Katika mazoezi yafuatayo, grafu kwa kutumia intercepts.

    1. -x + 5y = 10
    2. -x + 4y = 8
    3. x + 2y = 4
    4. x + 2y = 6
    5. x + y = 2
    6. x + y = 5
    7. x + y = -3
    8. x + y = -1
    9. x - y = 1
    10. x - y = 2
    11. x - y = -4
    12. x - y = -3
    13. 4x + y = 4
    14. 3x + y = 3
    15. 3x - y = -6
    16. 2x - y = -8
    17. 2x + 4y = 12
    18. 3x + 2y = 12
    19. 3x-2y = 6
    20. 5x-2y = 10
    21. 2x-5y = -20
    22. 3x-4y = -12
    23. y = -2x
    24. y = -4x
    25. y = x
    26. y = 3x

    Chagua Njia rahisi zaidi ya Grafu ya Mstari

    Katika mazoezi yafuatayo, tambua njia rahisi zaidi ya kuchora kila mstari.

    1. x = 2
    2. y = 4
    3. y = 5
    4. x = -3
    5. y = -3x + 4
    6. y = -5x + 2
    7. x - y = 5
    8. x - y = 1
    9. y =\(\dfrac{2}{3}\) x-1
    10. y =\(\dfrac{4}{5}\) x-3
    11. y = -3
    12. y = -1
    13. 3x-2y = -12
    14. 2x-5y = -10
    15. y =\(− \dfrac{1}{4}\) x + 3
    16. y =\(− \dfrac{1}{3}\) x + 5

    kila siku Math

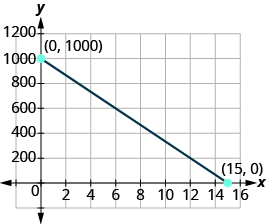
    1. Safari ya barabara Damien anaendesha gari kutoka Chicago hadi Denver, umbali wa maili 1,000. Mhimili wa x-kwenye grafu hapa chini unaonyesha muda katika masaa tangu Damien aliondoka Chicago. Mhimili wa y unawakilisha umbali alioacha kuendesha gari.
      1. Kupata x- na y- intercepts.
      2. Eleza nini x- na y- intercepts maana kwa Damien.

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka - hadi. Mstari hupita kupitia pointi zilizoandikwa “jozi iliyoamuru 0, 1000" na “jozi iliyoamriwa 15, 0”.

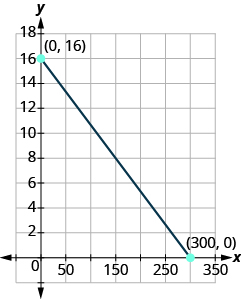
    1. Safari ya barabara Ozzie alijaza tank ya gesi ya lori lake na akaenda safari ya barabara. x-mhimili kwenye grafu inaonyesha idadi ya maili Ozzie alimfukuza tangu kujaza up. Mhimili wa y unawakilisha idadi ya galoni za gesi katika tank ya gesi ya lori.
      1. Kupata x- na y- intercepts.
      2. Eleza nini x- na y- intercepts maana kwa Ozzie.

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka - hadi. mstari hupita kwa njia ya alama labeled “kuamuru jozi 0, 16" na “kuamuru jozi 300, 0”.

    Mazoezi ya kuandika

    1. Je, unapataje x-intercept ya grafu ya 3x-2y = 6?
    2. Je, unapataje y-intercept ya grafu ya 5x - y = 10?
    3. Je! Unapendelea grafu ya equation 4x + y = -4 kwa kupanga pointi au intercepts? Kwa nini?
    4. Je, ungependa grafu equation y =\(\dfrac{2}{3}\) x - 2 kwa kupanga pointi au intercepts? Kwa nini?

    Self Check

    (a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

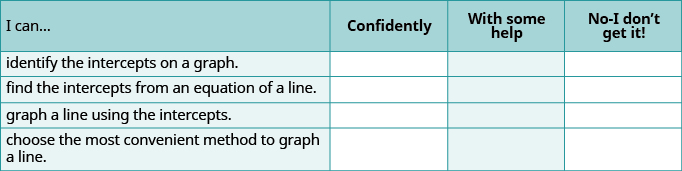
    CNX_BMath_Figure_AppB_068.jpg

    (b) Orodha hii inakuambia nini kuhusu ustadi wako wa sehemu hii? Ni hatua gani utachukua ili kuboresha?

    Wachangiaji na Majina