Skip to main content
Global

11.5: Graphing na Intercepts (Sehemu ya 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    173372

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Tambua intercepts kwenye grafu
    • Kupata intercepts kutoka equation ya mstari
    • Graph mstari kwa kutumia intercepts
    • Chagua njia rahisi zaidi ya kuchora mstari
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Tatua: 3x + 4y = -12 kwa x wakati y = 0. Ikiwa umekosa tatizo hili, tathmini Mfano 9.11.6.
    2. Je, ni hatua (0, -5) kwenye mhimili wa x au y-axis? Ikiwa umekosa tatizo hili, tathmini Mfano 11.1.5.
    3. Ambayo jozi zilizoamriwa ni ufumbuzi wa equation 2x - y = 6? (a) (6, 0) (b) (0, -6) (c) (4, -2). Ikiwa umekosa tatizo hili, tathmini Mfano 11.2.8.

    Tambua Intercepts kwenye Grafu

    Kila equation linear ina mstari wa kipekee ambayo inawakilisha ufumbuzi wote wa equation. Wakati graphing line kwa pointi njama, kila mtu ambaye grafu line unaweza kuchagua pointi yoyote tatu, hivyo watu wawili graphing line wanaweza kutumia seti tofauti ya pointi.

    Kwa mtazamo wa kwanza, mistari yao miwili inaweza kuonekana tofauti tangu wangeweza kuwa na pointi tofauti zilizoandikwa. Lakini ikiwa kazi yote ilifanyika kwa usahihi, mistari itakuwa mstari sawa. Njia moja ya kutambua kwamba wao ni kweli mstari huo ni kuzingatia ambapo mstari unavuka shoka. Kila moja ya pointi hizi inaitwa intercept ya mstari.

    Ufafanuzi: Intercepts ya Line

    Kila moja ya pointi ambayo mstari unavuka mstari wa x-axis na y-axis inaitwa intercept ya mstari.

    Hebu tuangalie grafu ya mistari iliyoonyeshwa kwenye Kielelezo\(\PageIndex{1}\).

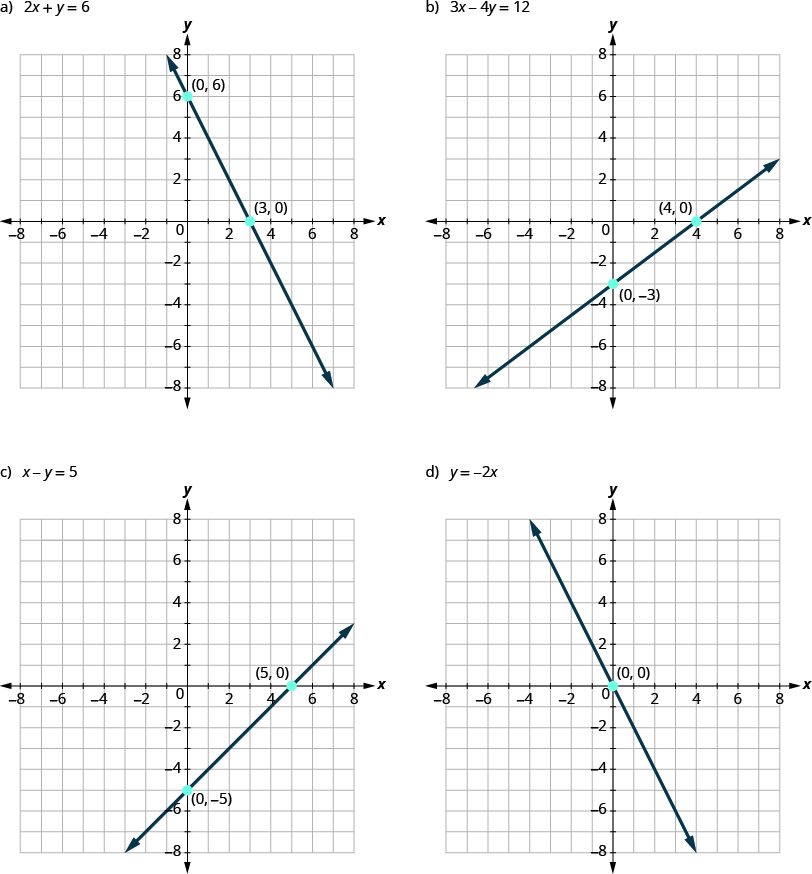
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. line hupita kwa njia ya pointi mbili labeled, “awali jozi 0, 6" na kuamuru jozi 3, 0”.

    Kielelezo\(\PageIndex{1}\)

    Kwanza, angalia ambapo kila mstari huu huvuka mstari wa x-:

    Jedwali\(\PageIndex{1}\)
    Kielelezo: Mstari unavuka mstari wa x-axis katika: Amri jozi ya hatua hii
    Kielelezo\(\PageIndex{1a}\) 3 (3,0)
    Kielelezo\(\PageIndex{1b}\) 4 (4,0)
    Kielelezo\(\PageIndex{1c}\) 5 (5,0)
    Kielelezo\(\PageIndex{1d}\) 0 (0,0)

    Je! Unaona mfano?

    Kwa kila mstari, kuratibu y ya uhakika ambapo mstari unavuka mstari wa x-axis ni sifuri. Hatua ambapo mstari unavuka mstari wa x-axis ina fomu (a, 0); na inaitwa x-intercept ya mstari. X-intercept hutokea wakati y ni sifuri.

    Sasa, hebu tuangalie pointi ambapo mistari haya huvuka mhimili y.

    Jedwali\(\PageIndex{2}\)
    Kielelezo: Mstari unavuka mstari wa x-axis katika: Amri jozi ya hatua hii
    Kielelezo\(\PageIndex{1a}\) 6 (0, 6)
    Kielelezo\(\PageIndex{1b}\) -3 (0, -3)
    Kielelezo\(\PageIndex{1c}\) -5 (0, -5)
    Kielelezo\(\PageIndex{1d}\) 0 (0, 0)
    Ufafanuzi: x-intercept na y-intercept ya mstari

    X-intercept ni hatua, (a, 0), ambapo grafu huvuka x-axis.

    X-intercept hutokea wakati y ni sifuri.

    Y-intercept ni hatua, (0, b), ambapo grafu huvuka mhimili wa y.

    Y-intercept hutokea wakati x ni sifuri.

    Mfano\(\PageIndex{1}\)

    Pata x- na y-intercepts ya kila mstari:

    (a) x + 2y = 4

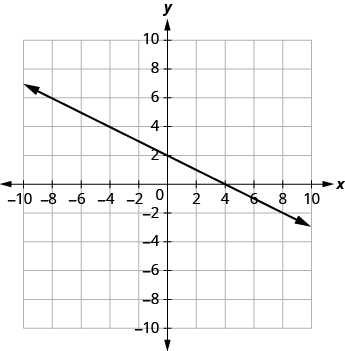
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa 4, 0”.

    (b) 3x - y = 6

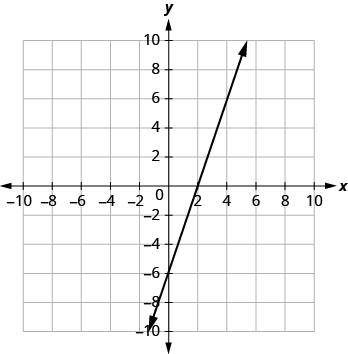
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, -6" na “jozi iliyoamriwa 2, 0”.

    (c) x + y = -5

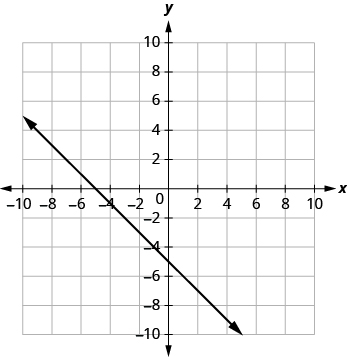
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. mstari hupita kupitia pointi “kuamuru jozi 0, -5" na “kuamuru jozi -5, 0”.

    Suluhisho

    (a)

    Grafu huvuka mstari wa x-axis kwa uhakika (4, 0). X-intercept ni (4, 0).
    Grafu huvuka mhimili wa y kwa uhakika (0, 2). X-intercept ni (0, 2).

    (b)

    Grafu huvuka mstari wa x-axis kwa uhakika (2, 0). X-intercept ni (2, 0).
    Grafu huvuka mhimili wa y kwa uhakika (0, -6). X-intercept ni (0, -6).

    (c)

    Grafu huvuka mstari wa x-axis kwa uhakika (-5, 0). X-intercept ni (-5, 0).
    Grafu huvuka mhimili wa y kwa uhakika (0, -5). X-intercept ni (0, -5).
    Zoezi\(\PageIndex{1A}\)

    Pata x- na y-intercepts ya grafu: x - y = 2.

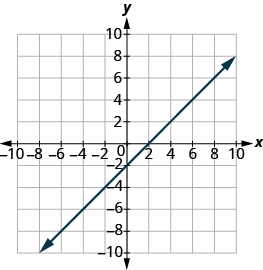
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa 2, 0”.

    Jibu

    x-intercept (2,0); y-intercept (0, -2)

    Zoezi\(\PageIndex{1B}\)

    Pata x- na y-intercepts ya grafu: 2x + 3y = 6.

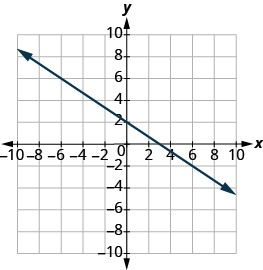
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa 3, 0”.

    Jibu

    x-intercept (3,0); y-intercept (0,2)

    Kupata Intercepts kutoka Equation ya Line

    Kutambua kwamba x-intercept hutokea wakati y ni sifuri na kwamba y-intercept hutokea wakati x ni sifuri inatupa njia ya kupata intercepts ya mstari kutoka equation yake. Ili kupata x-intercept, basi y = 0 na kutatua kwa x Ili kupata y-intercept, basi x = 0 na kutatua kwa y.

    Ufafanuzi: Pata x na y kutoka kwa Equation ya Line

    Tumia equation ili kupata:

    • x-intercept ya mstari, basi y = 0 na kutatua kwa x.
    • y-intercept ya mstari, basi x = 0 na kutatua kwa y
    Jedwali\(\PageIndex{3}\)
    x y
      0
    0  
    Mfano\(\PageIndex{2}\)

    Pata intercepts ya 2x + y = 6

    Suluhisho

    Tutajaza Kielelezo\(\PageIndex{2}\).

    ...

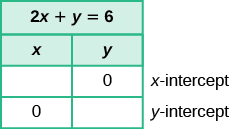
    Kielelezo\(\PageIndex{2}\)

    Ili kupata x- intercept, basi y = 0:

    Mbadala 0 kwa y. \(2x + \textcolor{red}{0} = 6\)
    Ongeza. 2x = 6
    Gawanya na 2. x = 3

    X-intercept ni (3, 0).

    Ili kupata y- intercept, basi x = 0:

    mbadala 0 kwa x. \(2 \cdot \textcolor{red}{0} + y = 6\)
    Kuzidisha. 0 + y = 6
    Ongeza. y = 6

    Y-intercept ni (0, 6).

    2x + y = 6
    x y
    3 0
    0 6

    Kielelezo\(\PageIndex{3}\)

    Intercepts ni pointi (3, 0) na (0, 6).

    Zoezi\(\PageIndex{2A}\)

    Pata intercepts: 3x + y = 12.

    Jibu

    x-intercept (4,0); y-kukatiza (0,12)

    Zoezi\(\PageIndex{2B}\)

    Pata intercepts: x + 4y = 8.

    Jibu

    x-intercept (8,0); y-intercept (0,2)

    Mfano\(\PageIndex{3}\)

    Kupata intercepts ya 4x-3y = 12.

    Suluhisho

    Ili kupata x-intercept, basi y = 0.

    Mbadala 0 kwa y. 4x - 3 • 0 = 12
    Kuzidisha. 4x - 0 = 12
    Ondoa. 4x = 12
    Gawanya na 4. x = 3

    Y-intercept ni (0, -4). Mikataba ni pointi (-3, 0) na (0, -4).

    4x - 3y = 12
    x y
    3 0
    0 -4
    Zoezi\(\PageIndex{3A}\)

    Pata intercepts ya mstari: 3x-4y = 12.

    Jibu

    x-intercept (4,0); y-kukatiza (0, -3)

    Zoezi\(\PageIndex{3B}\)

    Pata intercepts ya mstari: 2x-4y = 8.

    Jibu

    x-intercept (4,0); y-intercept (0, -2)

    Grafu Mstari Kutumia Intercepts

    Ili grafu equation linear kwa pointi njama, unaweza kutumia intercepts kama mbili ya pointi yako tatu. Kupata intercepts mbili, na kisha hatua ya tatu ili kuhakikisha usahihi, na kuteka mstari. Njia hii mara nyingi ni njia ya haraka ya kuchora mstari.

    Mfano\(\PageIndex{4}\)

    Grafu -x + 2y = 6 kwa kutumia intercepts.

    Suluhisho

    Kwanza, tafuta x-intercept. Hebu y = 0,

    \[\begin{split} -x + 2y &= 6 \\ -x + 2(0) &= 6 \\ -x &= 6 \\ x &= -6 \end{split}\]

    X-intercept ni (—6, 0).

    Sasa tafuta y-intercept. Hebu x = 0.

    \[\begin{split} -x + 2y &= 6 \\ -0 + 2y &= 6 \\ 2y &= 6 \\ y &= 3 \end{split}\]

    Y-intercept ni (0, 3).

    Pata hatua ya tatu. Tutatumia x = 2,

    \[\begin{split} -x + 2y &= 6 \\ -2 + 2y &= 6 \\ 2y &= 8 \\ y &= 4 \end{split}\]

    Suluhisho la tatu kwa equation ni (2, 4).

    Fupisha pointi tatu katika meza na kisha uwapange kwenye grafu.

    -x + 2y = 6
    x y (x, y)
    -6 0 (-6, 0)
    0 3 (0, 3)
    2 4 (2, 4)

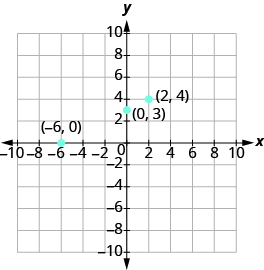
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -10 hadi 10. Vipengele vitatu vilivyoandikwa vinaonyeshwa kwenye “jozi iliyoamriwa -6, 0”, “jozi iliyoamriwa 0, 3" na “jozi iliyoamriwa 2, 4”.

    Je, pointi zinaendelea? Ndiyo, hivyo futa mstari kupitia pointi.

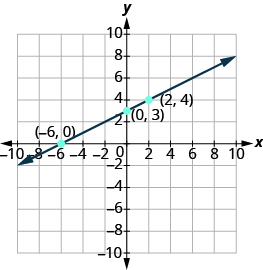
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -10 hadi 10. Vipengele vitatu vilivyoandikwa vinaonyeshwa kwenye “jozi iliyoamriwa -6, 0”, “jozi iliyoamriwa 0, 3" na “jozi iliyoamriwa 2, 4”. Mstari unapita kupitia pointi tatu zilizoandikwa.

    Zoezi\(\PageIndex{4A}\)

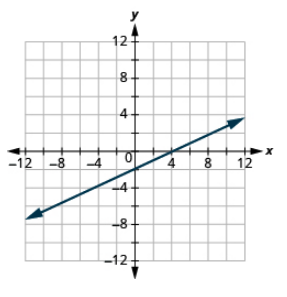
    Graph mstari kwa kutumia intercepts: x-2y = 4.

    Jibu
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, -2” na “jozi iliyoamriwa 4, 0”.
    Zoezi\(\PageIndex{4B}\)

    Graph mstari kwa kutumia intercepts: -x + 3y = 6.

    Jibu

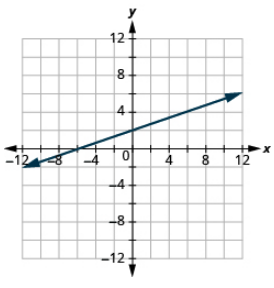
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa -6, 0”.

    JINSI YA: GRAFU MSTARI KWA KUTUMIA INTERCEPTS

    Hatua ya 1. Pata x - na y-intercepts ya mstari.

    • Hebu y = 0 na kutatua kwa x.
    • Hebu x = 0 na kutatua kwa y.

    Hatua ya 2. Kupata ufumbuzi wa tatu kwa equation.

    Hatua ya 3. Plot pointi tatu na kisha kuangalia kwamba wao line up.

    Hatua ya 4. Chora mstari.

    Mfano\(\PageIndex{5}\)

    Grafu 4x-3y = 12 kutumia intercepts.

    Suluhisho

    Pata intercepts na hatua ya tatu.

    $$\ kuanza {kupasuliwa} x-intercept,\; &basi\; y = 0\\ 4x - 3y &= 12\\ 4x - 3 (\ textcolor {nyekundu} {0}) &= 12\\ 4x &= 12\\ x &= 3\ mwisho {mgawanyiko} $$ $$\ kuanza {kupasuliwa} y-intercept,\; &basi\; x = 0\\ 4x - 3y &= 12\\ 4 (\ rangi ya maandishi {nyekundu} {0}) - 3y &= 12\\ 4x - 3 (\ rangi ya maandishi {nyekundu} {4}) &= 12\\ y &= -4\ mwisho {mgawanyiko} $$ $$\ kuanza {mgawanyiko} tatu\; uhakika,\; &basi\; y = 4\\ 4x - 3y &= 12\\ 4x - 12 &= 12\\ 4x &= 24\\ x &= 6\ mwisho {mgawanyiko} $$

    Tunaorodhesha pointi na kuonyesha grafu.

    4x - 3y = 12
    x y (X. y)
    3 0 (3, 0)
    0 -4 (0, -4)
    6 4 (6, 4)

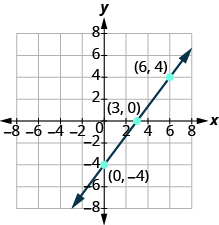
    Grafu inaonyesha ndege ya kuratibu x y. Axes zote mbili zinaendesha kutoka -7 hadi 7. Tatu pointi unlabeled ni inayotolewa katika “kuamuru jozi 0, -4”, “kuamuru jozi 3, 0” na “kuamuru jozi 6, 4”. Mstari unapita kupitia pointi.

    Zoezi\(\PageIndex{5A}\)

    Graph mstari kwa kutumia intercepts: 5x-2y = 10.

    Jibu

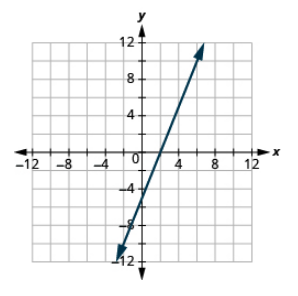
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. mstari hupita kupitia pointi “kuamuru jozi 0, -5" na “kuamuru jozi 2, 0”.

    Zoezi\(\PageIndex{5B}\)

    Graph mstari kwa kutumia intercepts: 3x-4y = 12.

    Jibu

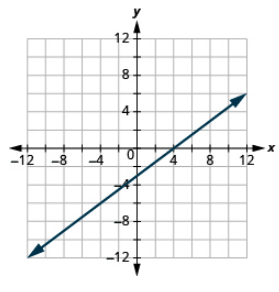
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, -3” na “jozi iliyoamriwa 4, 0”.

    Mfano\(\PageIndex{6}\)

    Grafu\(y = 5x\) kwa kutumia intercepts.

    Suluhisho

    $$\ kuanza {mgawanyiko} x-intercept;\; &Hebu\; y = 0\ ldotp\\ y &= 5x\\ textcolor {nyekundu} {0} &= 5x\\ 0 &= x\\ x &= 0\\ The\; x-intercept\; &ni\; (0, 0)\ ldotp\ mwisho {mgawanyiko} $$ $$\ kuanza {mgawanyiko} y-intercept;\; &Hebu\; x = 0\ ldotp\\ y &= 5x\\ y &= 5 (\ textcolor {nyekundu} {0})\\ y &= 0\\ The\; y-intercept\; &ni\; (0, 0)\ ldotp\ mwisho {mgawanyiko} $$

    Mstari huu una kizuizi kimoja tu! Ni hatua (0, 0).

    Ili kuhakikisha usahihi, tunahitaji kupanga njama tatu. Kwa kuwa intercepts ni hatua sawa, tunahitaji pointi mbili zaidi kwa grafu mstari. Kama siku zote, tunaweza kuchagua maadili yoyote kwa x, hivyo tutaweza basi x kuwa 1 na -1.

    $$\ kuanza {split} x &= 1\\ y &= 5x\\ y &= 5 (\ textcolor {nyekundu} {1})\\ y &= 5\\ (1, &-5)\ mwisho {mgawanyiko} $$ $$\ kuanza {split} x &= -1\\ y &= 5x\\ y &= 5 (\ textcolor {nyekundu} {-1})\\ y &= -5\ (-1, &-5)\ mwisho {mgawanyiko} $$

    Panga pointi katika meza.

    y = 5x
    x y (x, y)
    0 0 (0, 0)
    1 5 (1, 5)
    -1 -5 (-1, -5)

    Panda pointi tatu, angalia kwamba wao line up, na kuteka mstari.

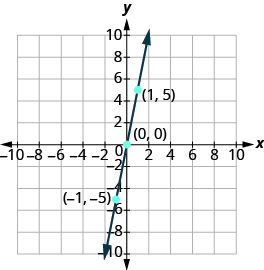
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -10 hadi 10. line hupita kwa njia ya pointi tatu labeled, “awali jozi -1, -5", “awali jozi 0, 0”, na kuamuru jozi 1, 5”.

    Zoezi\(\PageIndex{6A}\)

    Grafu kwa kutumia intercepts:\(y = 3x\).

    Jibu

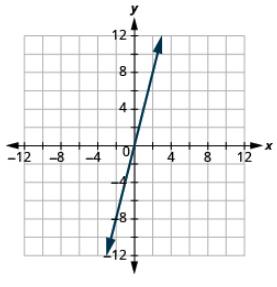
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 0” na “jozi iliyoamriwa 1, 3".

    Zoezi\(\PageIndex{6B}\)

    Grafu kwa kutumia intercepts:\(y = − x\).

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 0” na “jozi iliyoamriwa 1, -1”.

    Wachangiaji na Majina