Skip to main content
Global

11.4: Graphing Linear equations (Sehemu ya 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    173381

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Grafu Mstari wa Wima na Ulalo

    Je, tunaweza graph equation na variable moja tu? Tu x na hakuna y, au tu y bila x? Tutafanyaje meza ya maadili ili kupata pointi za kupanga njama?

    Hebu fikiria equation x = -3. Equation inasema kuwa x daima ni sawa na -3, hivyo thamani yake haitegemei y.Bila kujali y ni nini, thamani ya x ni daima -3.

    Ili kufanya meza ya ufumbuzi, tunaandika -3 kwa maadili yote x. Kisha chagua maadili yoyote kwa y Tangu x haitegemei y, unaweza kuchagua namba yoyote unayopenda. Lakini kwa kifafa ukubwa wa grafu yetu kuratibu, tutaweza kutumia 1, 2, na 3 kwa kuratibu y-kama inavyoonekana katika meza.

    x = -3
    x y (x, y)
    -3 1 (-3, 1)
    -3 2 (-3, 2)
    -3 3 (-3, 3)

    Kisha njama pointi na uunganishe kwa mstari wa moja kwa moja. Angalia katika Kielelezo\(\PageIndex{5}\) kwamba grafu ni mstari wa wima.

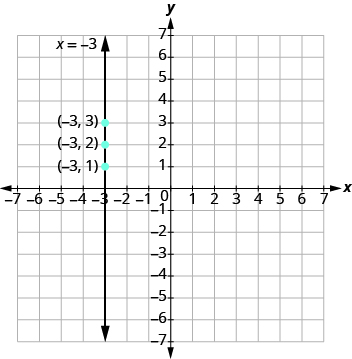
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari wa wima unapita kupitia pointi tatu zilizoandikwa, “jozi iliyoamriwa -3, 3", “iliamuru jozi -3, 2", na kuamuru jozi -3, 1”. Mstari umeandikwa x = -3.

    Kielelezo\(\PageIndex{5}\)

    Ufafanuzi: mstari wa wima

    Mstari wa wima ni grafu ya equation ambayo inaweza kuandikwa kwa fomu x = a. mstari hupita kwa njia ya x -axis katika (a, 0).

    Mfano\(\PageIndex{6}\):

    Grafu equation x = 2. Ni aina gani ya mstari inaunda?

    Suluhisho

    equation ina variable tu, x, na x daima ni sawa na 2. Tunafanya meza ambapo x daima ni 2 na tunaweka maadili yoyote kwa y.

    x = -3
    x y (x, y)
    2 1 (2, 1)
    2 2 (2, 2)
    2 3 (2, 3)

    Panda pointi na uunganishe kama inavyoonekana.

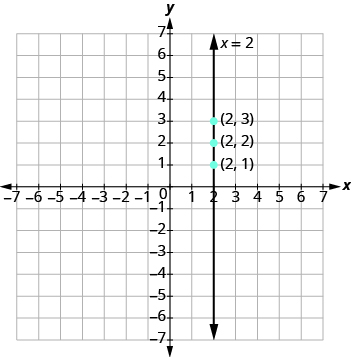
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari wa wima unapita kupitia pointi tatu zilizoandikwa, “jozi iliyoamriwa 2, 3", “iliamuru jozi 2, 2", na kuamuru jozi 2, 1”. Mstari umeandikwa x = 2.

    Grafu ni mstari wa wima unaopita kupitia x -axis saa 2.

    Zoezi\(\PageIndex{10}\):

    Grafu equation: x = 5.

    Jibu

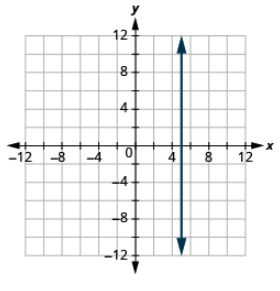
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari wa wima unapita kupitia pointi “jozi iliyoamriwa 5, 0” na “jozi iliyoamriwa 5, 1”.

    Zoezi\(\PageIndex{11}\):

    Grafu equation: x = π-2.

    Jibu

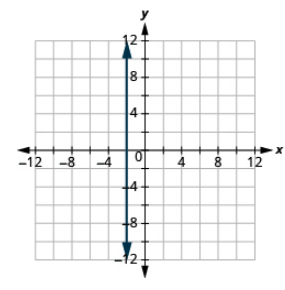
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari wa wima hupita kupitia pointi “jozi iliyoamriwa -2, 0” na “jozi iliyoamriwa -2, 1”.

    Nini kama equation ina y lakini hakuna x? Hebu graph equation y = 4. Wakati huu y -thamani ni mara kwa mara, hivyo katika y equation hii hautegemei x.

    Ili kufanya meza ya ufumbuzi, weka 4 kwa maadili yote y na kisha uchague maadili yoyote kwa x.

    Tutaweza kutumia 0, 2, na 4 kwa x - maadili.

    x = -3
    x y (x, y)
    0 4 (0, 4)
    2 4 (2, 4)
    4 4 (4, 4)

    Panda pointi na uunganishe, kama inavyoonekana kwenye Mchoro\(\PageIndex{6}\). Grafu hii ni mstari usio na usawa unaopita kupitia mhimili wa y saa 4.

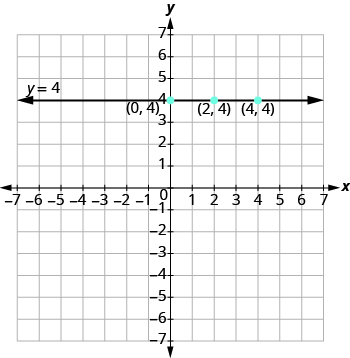
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari wa usawa unapita kupitia pointi tatu zilizoandikwa, “jozi iliyoamriwa 0, 4", “iliamuru jozi 2, 4", na kuamuru jozi 4, 4”. Mstari umeandikwa y = 4.

    Kielelezo\(\PageIndex{6}\)

    Ufafanuzi: Line ya usawa

    Mstari wa usawa ni grafu ya equation ambayo inaweza kuandikwa kwa fomu y = b. mstari hupita kupitia y mhimili katika (0, b).

    Mfano\(\PageIndex{7}\):

    Grafu equation y = -1.

    Suluhisho

    Equation y = -1 ina variable tu, y. thamani ya y ni mara kwa mara. Jozi zote zilizoamriwa katika meza zina y -kuratibu sawa, -1. Tunachagua 0, 3, na -3 kama maadili ya x.

    x = -3
    x y (x, y)
    -3 -1 (-3, -1)
    0 -1 (0, -1)
    3 -1 (3, -1)

    Grafu ni mstari usio na usawa unaopitia y -axis saa -1 kama inavyoonyeshwa.

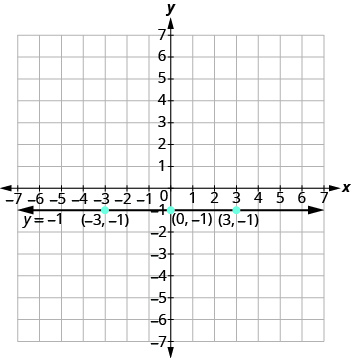
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari wa usawa unapita kupitia pointi tatu zilizoandikwa, “jozi iliyoamriwa -3, -1”, “jozi iliyoamriwa 0, -1”, na kuamuru jozi 3, -1”. Mstari umeandikwa y = -1.

    Zoezi\(\PageIndex{12}\):

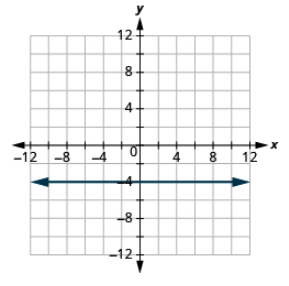
    Grafu equation: y = -4.

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari wa usawa unapita kupitia pointi “jozi iliyoamriwa 0, -4” na “jozi iliyoamriwa 1, -4”.

    Zoezi\(\PageIndex{13}\):

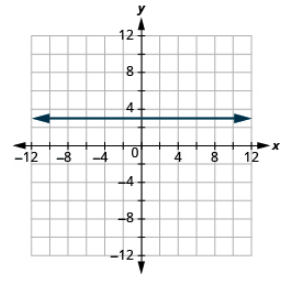
    Grafu equation: y = 3.

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari wa usawa unapita kupitia pointi “jozi iliyoamriwa 0, 3" na “jozi iliyoamriwa 1, 3".

    Milinganyo kwa mistari ya wima na ya usawa inaonekana sawa na milinganyo kama y = 4x. Ni tofauti gani kati ya equations y = 4x na y = 4?

    Equation y = 4x ina wote x na y. thamani ya y inategemea thamani ya x. y-kuratibu mabadiliko kulingana na thamani ya x.

    Equation y = 4 ina variable moja tu. Thamani ya y ni mara kwa mara. Kuratibu y-daima ni 4. Haitegemei thamani ya x.

    y = 4x
    x y (x, y)
    0 0 (0, 0)
    1 4 (1, 4)
    2 8 (2, 8)
    \(\textcolor{red}{y = 4}\)
    \ (\ textcolor {nyekundu} {y = 4}\) "> x y (x, y)
    \ (\ textcolor {nyekundu} {y = 4}\) "> 0 4 (0, 4)
    \ (\ textcolor {nyekundu} {y = 4}\) "> 1 4 (1, 4)
    \ (\ textcolor {nyekundu} {y = 4}\) "> 2 4 (2, 4)

    Grafu inaonyesha equations zote mbili.

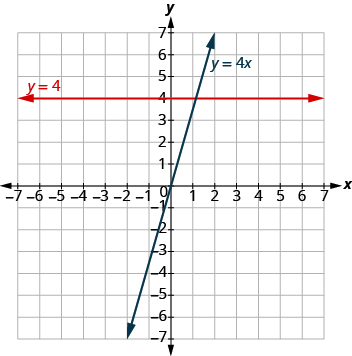
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari wa usawa unapita kupitia “jozi iliyoamriwa 0, 4" na “jozi iliyoamriwa 1, 4" na imeandikwa y = 4. mstari wa pili hupita kwa njia ya “awali jozi 0, 0” na “kuamuru jozi 1, 4" na kinachoitwa y = 4 x. mistari miwili intersect katika “awali jozi 1, 4”.

    Kumbuka kwamba equation y = 4x inatoa line iliyopandwa wakati y = 4 inatoa mstari usawa.

    Mfano\(\PageIndex{8}\):

    Grafu y = -3x na y = -3 katika mfumo huo wa kuratibu mstatili.

    Suluhisho

    Kupata ufumbuzi tatu kwa kila equation. Kumbuka kwamba equation kwanza ina variable x, wakati wa pili hana. Ufumbuzi wa equations zote mbili zimeorodheshwa.

    \(\textcolor{red}{y = -3x}\)
    \ (\ textcolor {nyekundu} {y = -3x}\) "> x y (x, y)
    \ (\ textcolor {nyekundu} {y = -3x}\) "> 0 0 (0, 0)
    \ (\ textcolor {nyekundu} {y = -3x}\) "> 1 -3 (1, -3)
    \ (\ textcolor {nyekundu} {y = -3x}\) "> 2 -6 (2, -6)
    y = -3
    x y (x, y)
    0 -3 (0, -3)
    1 -3 (1, -3)
    2 -3 (2, -3)

    Grafu inaonyesha equations zote mbili.

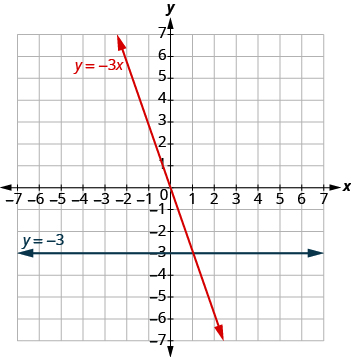
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari wa usawa unapita kupitia “jozi iliyoamriwa 0, -3” na “jozi iliyoamriwa 1, -3” na imeandikwa y = -3. mstari wa pili hupita kwa njia ya “awali jozi 0, 0” na “kuamuru jozi 1, -3” na kinachoitwa y = -3 x. mistari miwili intersect katika “awali jozi 1, -3”.

    Zoezi\(\PageIndex{14}\):

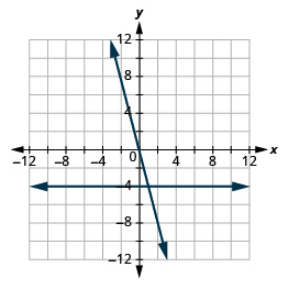
    Grafu milinganyo katika mfumo huo wa kuratibu mstatili: y = -4x na y = -4.

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari wa usawa unapita kupitia “jozi iliyoamriwa 0, -4” na “jozi iliyoamriwa 1, -4”. Mstari wa pili unapita kupitia “jozi iliyoamriwa 0, 0” na “jozi iliyoamriwa 1, -4”. mistari mbili intersect katika “kuamuru jozi 1, -4”.

    Zoezi\(\PageIndex{15}\):

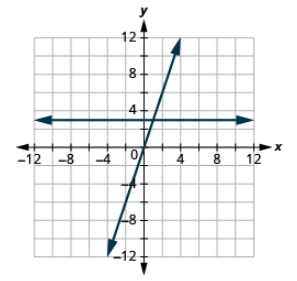
    Grafu equations katika mfumo huo wa kuratibu mstatili: y = 3 na y = 3x.

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari wa usawa unapita kupitia “jozi iliyoamriwa 0, 3" na “jozi iliyoamriwa 1, 3". Mstari wa pili unapita kupitia “jozi iliyoamriwa 0, 0” na “jozi iliyoamriwa 1, 3". mistari mbili intersect katika “kuamuru jozi 1, 3".

    PATA RASILIMALI ZA ZIADA

    Tumia Jedwali la Maadili

    Grafu Equation Linear Kuhusisha Fractions

    Grafu Mipangilio ya usawa na ya Wima

    Mazoezi hufanya kamili

    Tambua Uhusiano Kati ya Ufumbuzi wa Equation na Grafu yake

    Kwa kila jozi kuamuru, kuamua (a) ni jozi kuamuru ufumbuzi wa equation? (b) ni hatua kwenye mstari?

    1. y = x + 2
      1. (0, 2)
      2. (1, 2)
      3. (- 1, 1)
      4. (- 3, 1)
    2. y = x - 4
      1. (0, -4)
      2. (3, - 1)
      3. (2, 2)
      4. (1, - 5)
    3. y =\(\dfrac{1}{2}\) x - 3
      1. (0, -3)
      2. (2, - 2)
      3. (- 2, - 4)
      4. (4, 1)
    4. y =\(\dfrac{1}{3}\) x + 2
      1. (0, 2)
      2. (3, 3)
      3. (- 3, 2)
      4. (- 6, 0)

    Grafu Ulinganisho wa Mstari na Pointi za Kupanga

    Katika mazoezi yafuatayo, grafu kwa pointi za kupanga.

    1. y = 3x - 1
    2. y = 2x + 3
    3. y = -2x + 2
    4. y = -3x + 1
    5. y = x + 2
    6. y = x - 3
    7. y = - x - 3
    8. y = - x - 2
    9. y = 2x
    10. y = 3x
    11. y = -4x
    12. y = -2x
    13. y =\(\dfrac{1}{2}\) x + 2
    14. y =\(\dfrac{1}{3}\) x - 1
    15. y =\(\dfrac{4}{3}\) x - 5
    16. y =\(\dfrac{3}{2}\) x - 3
    17. y =\(− \dfrac{2}{5}\) x + 1
    18. y =\(− \dfrac{4}{5}\) x - 1
    19. y =\(− \dfrac{3}{2}\) x + 2
    20. y =\(− \dfrac{5}{3}\) x + 4
    21. x + y = 6
    22. x + y = 4
    23. x + y = -3
    24. x + y = -2
    25. x - y = 2
    26. x - y = 1
    27. x - y = -1
    28. x - y = -3
    29. -x + y = 4
    30. -x + y = 3
    31. -x - y = 5
    32. -x - y = 1
    33. 3x + y = 7
    34. 5x + y = 6
    35. 2x + y = -3
    36. 4x + y = -5
    37. 2x + 3y = 12
    38. 3x - 4y = 12
    39. \(\dfrac{1}{3}\)x + y = 2
    40. \(\dfrac{1}{2}\)x + y = 3

    Grafu mistari ya wima na ya usawa

    Katika mazoezi yafuatayo, graph mistari ya wima na ya usawa.

    1. x = 4
    2. x = 3
    3. x = -2
    4. x = -5
    5. y = 3
    6. y = 1
    7. y = -5
    8. y = -2
    9. x =\(\dfrac{7}{3}\)
    10. x =\(\dfrac{5}{4}\)

    Katika mazoezi yafuatayo, grafu kila jozi ya equations katika mfumo huo wa kuratibu mstatili.

    1. y =\(− \dfrac{1}{2}\) x na y =\(− \dfrac{1}{2}\)
    2. y =\(− \dfrac{1}{3}\) x na y =\(− \dfrac{1}{3}\)
    3. y = 2x na y = 2
    4. y = 5x na y = 5

    Mazoezi ya mchanganyiko

    Katika mazoezi yafuatayo, grafu kila equation.

    1. y = 4x
    2. y = 2x
    3. y =\(− \dfrac{1}{2}\) x + 3
    4. y =\(\dfrac{1}{4}\) x - 2
    5. y = - x
    6. y = x
    7. x - y = 3
    8. x + y = - 5
    9. 4x + y = 2
    10. 2x + y = 6
    11. y = -1
    12. y = 5
    13. 2x + 6y = 12
    14. 5x + 2y = 10
    15. x = 3
    16. x = -4

    kila siku Math

    1. Motor nyumbani gharama Robinsons kukodi motor nyumbani kwa wiki moja kwenda likizo. Iliwapa $594 pamoja na $0.32 kwa maili kukodisha nyumba ya magari, hivyo equation ya mstari y = 594 + 0.32x inatoa gharama, y, kwa kuendesha gari x maili. Tumia gharama ya kukodisha kwa kuendesha gari maili 400, 800, na 1,200, halafu graph mstari.
    2. Kupata kila wiki Katika nyumba ya sanaa ya sanaa ambako anafanya kazi, Salvador analipwa $200 kwa wiki pamoja na 15% ya mauzo anayofanya, hivyo equation y = 200 + 0.15x inatoa kiasi y anachopata kwa kuuza dola x za mchoro. Tumia kiasi cha Salvador kinachopata kwa kuuza $900, $1,600, na $2,000, na kisha graph mstari.

    Mazoezi ya kuandika

    1. Eleza jinsi ungependa kuchagua tatu x-maadili kufanya meza ya grafu line y =\(\dfrac{1}{5}\) x - 2.
    2. Ni tofauti gani kati ya usawa wa mstari wa wima na usawa?

    Self Check

    (a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

    CNX_BMath_Figure_AppB_067.jpg

    (b) Baada ya kuchunguza orodha hii, utafanya nini ili uwe na ujasiri kwa malengo yote?

    Wachangiaji na Mashtaka