Skip to main content
Global

11.3: Graphing Linear equations (Sehemu ya 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    173373

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Tambua uhusiano kati ya ufumbuzi wa equation na grafu yake
    • Grafu equation ya mstari kwa pointi za kupanga
    • Grafu mistari ya wima na ya usawa
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Tathmini: 3x + 2 wakati x = -1. Ikiwa umekosa tatizo hili, tathmini Mfano 3.8.10.
    2. Tatua formula: 5x + 2y = 20 kwa y.Kama umekosa tatizo hili, tathmini Mfano 9.11.6.
    3. Kurahisisha:\(\dfrac{3}{8}\) (-24). Ikiwa umekosa tatizo hili, tathmini Mfano 4.3.10.

    Tambua Uhusiano Kati ya Ufumbuzi wa Equation na Grafu yake

    Katika Tumia Mfumo wa Kuratibu wa Rectangular, tulipata ufumbuzi machache kwa equation 3x + 2y = 6. Wao ni waliotajwa katika meza hapa chini. Kwa hiyo, jozi zilizoamriwa (0, 3), (2, 0)\(\left(1, \dfrac{3}{2}\right)\), (4, - 3), ni baadhi ya ufumbuzi wa equation 3x + 2y = 6. Tunaweza kupanga ufumbuzi huu katika mfumo wa kuratibu mstatili kama inavyoonekana kwenye grafu upande wa kulia.

    ...

    Angalia jinsi pointi zinavyosimama kikamilifu? Tunaunganisha pointi kwa mstari wa moja kwa moja ili kupata grafu ya equation 3x + 2y = 6. Angalia mishale kwenye mwisho wa kila upande wa mstari. Mishale hii inaonyesha mstari unaendelea.

    ...

    Kila hatua kwenye mstari ni suluhisho la equation. Pia, kila ufumbuzi wa equation hii ni hatua juu ya mstari huu. Pointi si kwenye mstari sio ufumbuzi!

    Kumbuka kwamba hatua ambayo kuratibu ni (- 2, 6) ni juu ya mstari inavyoonekana katika Kielelezo\(\PageIndex{1}\). Kama mbadala x = - 2 na y = 6 katika equation, kupata kwamba ni suluhisho la equation.

    ...

    Kielelezo\(\PageIndex{1}\)

    Hivyo (4, 1) si ufumbuzi wa equation 3x + 2y = 6. Kwa hiyo hatua (4, 1) si kwenye mstari. Huu ni mfano wa msemo huo, “Picha ina thamani ya maneno elfu.” Mstari unaonyesha ufumbuzi wote wa equation. Kila hatua kwenye mstari ni suluhisho la equation. Na, kila ufumbuzi wa equation hii ni juu ya mstari huu. Mstari huu unaitwa grafu ya equation 3x + 2y = 6.

    Ufafanuzi: Grafu ya Equation ya Mstari

    Grafu ya equation ya mstari Ax + By = C ni mstari wa moja kwa moja.

    • Kila hatua kwenye mstari ni suluhisho la equation.
    • Kila ufumbuzi wa equation hii ni hatua juu ya mstari huu.
    Mfano\(\PageIndex{1}\):

    Grafu ya y = 2x - 3 inavyoonyeshwa hapa chini.

    ...

    Kwa kila jozi kuamuru kuamua (a) Je jozi awali ufumbuzi wa equation? (b) Je, ni uhakika juu ya mstari?

    (a) (0, 3) (b) (3, ∙ 3) (c) (2, - 3) (d) (- 1, - 5)

    Suluhisho

    Badilisha x - na y -maadili katika equation kuangalia kama jozi kuamuru ni suluhisho la equation.

    (a)\[\begin{split} (a)&\; (\textcolor{blue}{0}, \textcolor{red}{-3}) \qquad \qquad \quad \; (b)\; (\textcolor{blue}{3}, \textcolor{red}{3}) \qquad \qquad \qquad \quad (c)\; (\textcolor{blue}{2}, \textcolor{red}{-3}) \qquad \qquad \qquad \quad (d)\; (\textcolor{blue}{-1}, \textcolor{red}{-5}) \\ y &= 2x - 3 \qquad \qquad \quad y = 2x - 3 \qquad \qquad \qquad \; y = 2x - 3 \qquad \qquad \qquad \; \; \; y = 2x - 3 \\ \textcolor{red}{-3} &\stackrel{?}{=} 2(\textcolor{blue}{0}) - 3 \qquad \qquad \; \textcolor{red}{3} \stackrel{?}{=} 2(\textcolor{blue}{3}) - 3 \qquad \qquad \; \textcolor{red}{-3} \stackrel{?}{=} 2(\textcolor{blue}{2}) - 3 \qquad \qquad \; \; \; \textcolor{red}{-5} \stackrel{?}{=} 2(\textcolor{blue}{-1}) - 3 \\ -3 &= -3\; \checkmark \qquad \qquad \quad \; \; 3 = 3\; \checkmark \qquad \qquad \qquad -3 \neq 1 \qquad \qquad \qquad \qquad -5 = -5\; \checkmark \\ (0, -3)\;& is\; a\; solution \ldotp \quad (3, 3)\; is\; a\; solution \ldotp \qquad (2, -3)\; is\; not\; a\; solution \ldotp \qquad (-1, -5)\; is\; a\; solution \ldotp \end{split}\]

    (b) Panga pointi A: (0, -3) B: (3, 3) C: (2, - 3) na D: (- 1, - 5). Vipengele (0, -3), (3, 3), na (- 1, -5) viko kwenye mstari y = 2x - 3, na uhakika (2, ∙ 3) hauko kwenye mstari.

    ...

    Vipengele ambavyo ni ufumbuzi wa y = 2x - 3 viko kwenye mstari, lakini hatua ambayo sio suluhisho sio kwenye mstari.

    Zoezi\(\PageIndex{1}\):

    Grafu ya y = 3x - 1 inavyoonyeshwa. Kwa kila jozi kuamuru, kuamua (a) ni jozi kuamuru ufumbuzi wa equation? (b) ni hatua kwenye mstari?

    ...

    1. (0, - 1)
    2. (2, 2)
    3. (3, - 1)
    4. (- 1, - 4)
    Jibu 1.

    a. ndiyo, b. hapana

    Jibu 2.

    a. hapana, b. hapana

    Jibu 3.

    a. hapana, b. hapana

    Jibu 4.

    a. ndiyo, b. ndiyo

    Grafu Ulinganisho wa Mstari na Pointi za Kupanga

    Kuna mbinu kadhaa ambazo zinaweza kutumika kwa grafu equation linear. Njia tuliyotumia mwanzoni mwa sehemu hii kwa grafu inaitwa pointi za kupanga, au Njia ya Point-Plotting.

    Hebu graph equation y = 2x + 1 kwa pointi njama. Tunaanza kwa kutafuta pointi tatu ambazo ni ufumbuzi wa equation. Tunaweza kuchagua thamani yoyote kwa x au y, na kisha kutatua kwa variable nyingine.

    Kwa kuwa y imetengwa upande wa kushoto wa equation, ni rahisi kuchagua maadili kwa x Tutatumia 0, 1, na -2 kwa x kwa mfano huu. Sisi badala ya kila thamani ya x katika equation na kutatua kwa y.

    Takwimu inaonyesha mbadala tatu za algebraic katika equation. Badala ya kwanza ni kwa x = -2, na -2 imeonyeshwa kwa bluu. Mstari unaofuata ni y = 2 x + 1. Mstari unaofuata ni y = 2 mabano ya wazi -2, yaliyoonyeshwa katika bluu, mabano yaliyofungwa, + 1. Mstari unaofuata ni y = - 4 + 1. Mstari unaofuata ni y = -3. Mstari wa mwisho ni “jozi iliyoamriwa -2, -3”. Badala ya pili ni kwa x = 0, na 0 inavyoonekana katika bluu. Mstari unaofuata ni y = 2 x + 1. Mstari unaofuata ni y = 2 mabano ya wazi 0, yaliyoonyeshwa katika bluu, mabano yaliyofungwa, + 1. Mstari unaofuata ni y = 0 + 1. Mstari unaofuata ni y = 1. Mstari wa mwisho ni “jozi iliyoamriwa 0, 2”. Badala ya tatu ni kwa x = 1, na 1 inavyoonekana katika bluu. Mstari unaofuata ni y = 2 x + 1. Mstari unaofuata ni y = 2 mabano ya wazi 1, yaliyoonyeshwa katika bluu, mabano yaliyofungwa, + 1. Mstari unaofuata ni y = 2 + 1. Mstari unaofuata ni y = 3. Mstari wa mwisho ni “jozi iliyoamriwa -1, 3".

    Tunaweza kuandaa ufumbuzi katika meza. Angalia Jedwali\(\PageIndex{1}\).

    Jedwali\(\PageIndex{1}\)
    y = 2x + 1
    x y (x, y)
    0 1 (0, 1)
    1 3 (1, 3)
    -2 -3 (-2, -3)

    Sasa tunapanga pointi kwenye mfumo wa kuratibu mstatili. Angalia kwamba pointi zinaendelea. Ikiwa hawakuwa na mstari, ingekuwa na maana tulifanya kosa na tunapaswa kuangalia mara mbili kazi yetu yote. Angalia Kielelezo\(\PageIndex{2}\).

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Tatu alama labeled ni umeonyesha, “kuamuru jozi -2, -3”, “awali jozi 0, 1”, na kuamuru jozi 1, 3".

    Kielelezo\(\PageIndex{2}\)

    Chora mstari kupitia pointi tatu. Panua mstari kujaza gridi ya taifa na kuweka mishale kwenye mwisho wa mstari. Mstari ni grafu ya y = 2x + 1.

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. line hupita kwa njia ya pointi tatu labeled, “kuamuru jozi -2, -3”, “awali jozi 0, 1”, na kuamuru jozi 1, 3".

    Kielelezo\(\PageIndex{3}\)

    JINSI YA: GRAFU EQUATION YA MSTARI KWA POINTI ZA KUPANGA

    Hatua ya 1. Pata pointi tatu ambazo kuratibu ni ufumbuzi wa equation. Kuwaandaa katika meza.

    Hatua ya 2. Panda pointi kwenye mfumo wa kuratibu mstatili. Angalia kwamba pointi zinaendelea. Ikiwa hawana, angalia kwa makini kazi yako.

    Hatua ya 3. Chora mstari kupitia pointi. Panua mstari kujaza gridi ya taifa na kuweka mishale kwenye mwisho wa mstari.

    Ni kweli kwamba inachukua pointi mbili tu kuamua mstari, lakini ni tabia nzuri ya kutumia pointi tatu. Ikiwa unapanga pointi mbili tu na mmoja wao si sahihi, bado unaweza kuteka mstari lakini hautawakilisha ufumbuzi wa equation. Itakuwa mstari usio sahihi. Ikiwa unatumia pointi tatu, na moja si sahihi, pointi hazitasimama. Hii inakuambia kitu kibaya na unahitaji kuangalia kazi yako. Angalia Kielelezo\(\PageIndex{4}\).

    Kuna takwimu mbili. Kielelezo a inaonyesha pointi tatu ambazo zote zilizomo kwenye mstari wa moja kwa moja. Kuna mstari na mishale iliyopita kupitia pointi tatu. Kielelezo b kinaonyesha pointi 3 ambazo sio zote zilizopangwa kwa mstari wa moja kwa moja.

    Kielelezo\(\PageIndex{4}\) - Angalia tofauti kati ya (a) na (b). All pointi tatu katika (a) line up ili tuweze kuteka mstari mmoja kwa njia yao. Pointi tatu katika (b) hazipatikani. Hatuwezi kuteka mstari mmoja wa moja kwa moja kupitia pointi zote tatu.

    Mfano\(\PageIndex{2}\):

    Grafu equation y = -3x.

    Suluhisho

    Pata pointi tatu ambazo ni ufumbuzi wa equation. Ni rahisi kuchagua maadili kwa x, na kutatua kwa y. unaona kwa nini?

    Takwimu inaonyesha mbadala tatu za algebraic katika equation. Badala ya kwanza ni kwa x = 0, na 0 inavyoonekana katika bluu. Mstari unaofuata ni y = -3 x. mstari unaofuata ni y = -3 wazi mabano 0, inavyoonekana katika bluu, imefungwa mabano. Mstari unaofuata ni y = 0. Mstari wa mwisho ni “jozi iliyoamriwa 0, 0”. Badala ya pili ni kwa x = 1, na 0 inavyoonekana katika bluu. Mstari unaofuata ni y = -3 x. mstari unaofuata ni y = -3 wazi mabano 1, inavyoonekana katika bluu, imefungwa mabano. Mstari unaofuata ni y = -3. Mstari wa mwisho ni “jozi iliyoamriwa 1, -3”. Badala ya tatu ni kwa x = -2, na -2 imeonyeshwa kwa bluu. Mstari unaofuata ni y = -3 x. mstari unaofuata ni y = -3 wazi mabano -2, inavyoonekana katika bluu, imefungwa mabano. Mstari unaofuata ni y = 6. Mstari wa mwisho ni “jozi iliyoamriwa -2, 6".

    Andika orodha katika meza.

    y = -3x
    x y (x, y)
    0 0 (0, 0)
    1 -3 (1, -3)
    -2 6 (-2, 6)

    Plot pointi, angalia kwamba wao line up, na kuteka mstari kama inavyoonekana.

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. Mstari unapita kupitia pointi tatu zilizoandikwa, “jozi iliyoamriwa -2, 6", “iliamuru jozi 0, 0”, na kuamuru jozi 1, -3”. Mstari umeandikwa y = -3 x.

    Zoezi\(\PageIndex{2}\):

    Grafu equation kwa pointi za kupanga: y = -4x.

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 0” na “jozi iliyoamriwa 4, -4”.
    Zoezi\(\PageIndex{3}\):

    Grafu equation kwa pointi njama: y = x.

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 0” na “jozi iliyoamuru 4, 4".

    Wakati equation ni pamoja na sehemu kama mgawo wa x, tunaweza kubadilisha idadi yoyote kwa x Lakini hesabu ni rahisi kama sisi kufanya 'nzuri' uchaguzi kwa ajili ya maadili ya x. njia hii sisi kuepuka majibu sehemu, ambayo ni vigumu graph usahihi.

    Mfano\(\PageIndex{3}\):

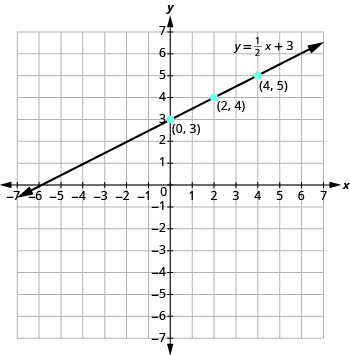
    Grafu equation y =\(\dfrac{1}{2}\) x + 3.

    Suluhisho

    Pata pointi tatu ambazo ni ufumbuzi wa equation. Kwa kuwa equation hii ina sehemu\(\dfrac{1}{2}\) kama mgawo wa x, tutachagua maadili ya x kwa makini. Tutatumia sifuri kama chaguo moja na mafungu ya 2 kwa uchaguzi mwingine.

    Takwimu inaonyesha mbadala tatu za algebraic katika equation. Badala ya kwanza ni kwa x = 0, na 0 inavyoonekana katika bluu. Mstari unaofuata ni y = 1 juu ya 2 x + 3. Mstari unaofuata ni y = 1 juu ya 2 mabano ya wazi 0, inavyoonekana katika bluu, mabano yaliyofungwa, + 3. Mstari unaofuata ni y = 3. Mstari wa mwisho ni “jozi iliyoamriwa 0, 3". Badala ya pili ni kwa x = 2, na 2 inavyoonekana katika bluu. Mstari unaofuata ni y = 1 juu ya 2 x + 3. Mstari unaofuata ni y = 1 juu ya 2 mabano wazi 2, inavyoonekana katika bluu, mabano yaliyofungwa, + 3. Mstari unaofuata ni y = 4. Mstari wa mwisho ni “jozi iliyoamriwa 2, 4". Badala ya tatu ni kwa x = 4, na 4 inavyoonekana katika bluu. Mstari unaofuata ni y = 1 juu ya 2 x + 3. Mstari unaofuata ni y = 1 juu ya 2 mabano ya wazi 4, inavyoonekana katika bluu, mabano yaliyofungwa, + 3. Mstari unaofuata ni y = 5. Mstari wa mwisho ni “jozi iliyoamriwa 4, 5”.

    Pointi zinaonyeshwa kwenye meza.

    y =\(\dfrac{1}{2}\) x + 3
    \ (\ dfrac {1} {2}\) x 3">x y (x, y)
    \ (\ dfrac {1} {2}\) x + 3">0 3 (0, 3)
    \ (\ dfrac {1} {2}\) x + 3"> 2 4 (2, 4)
    \ (\ dfrac {1} {2}\) x + 3"> 5 (4, 5)

    Plot pointi, angalia kwamba wao line up, na kuteka mstari kama inavyoonekana.

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. line hupita kwa njia ya pointi tatu labeled, “awali jozi 0, 3", “awali jozi 2, 4", na kuamuru jozi 4, 5”. Mstari umeandikwa y = 1 juu ya 2 x + 3.

    Zoezi\(\PageIndex{4}\):

    Grafu equation: y =\(\dfrac{1}{3}\) x - 1

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, -1” na “jozi iliyoamriwa 3, 0”.

    Zoezi\(\PageIndex{5}\):

    Grafu equation: y =\(\dfrac{1}{4}\) x + 2.

    Jibu

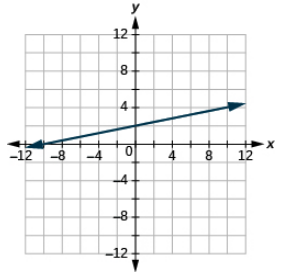
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 0, 2" na “jozi iliyoamriwa -4, 1”.

    Hadi sasa, equations wote sisi graphed alikuwa y kutolewa katika suala la x Sasa tutaweza graph equation na x na y upande huo.

    Mfano\(\PageIndex{4}\):

    Grafu equation x + y = 5.

    Suluhisho

    Pata pointi tatu ambazo ni ufumbuzi wa equation. Kumbuka, unaweza kuanza na thamani yoyote ya x au y.

    Takwimu inaonyesha mbadala tatu za algebraic katika equation. Badala ya kwanza ni kwa x = 0, na 0 inavyoonekana katika bluu. Mstari unaofuata ni x + y = 5. Mstari unaofuata ni 0, umeonyeshwa kwa bluu + y = 5. Mstari unaofuata ni y = 5. Mstari wa mwisho ni “jozi iliyoamriwa 0, 5”. Badala ya pili ni kwa x = 1, na 1 inavyoonekana katika bluu. Mstari unaofuata ni x + y = 5. Mstari unaofuata ni 1, umeonyeshwa kwa bluu + y = 5. Mstari unaofuata ni y = 4. Mstari wa mwisho ni “jozi iliyoamriwa 1, 4”. Badala ya tatu ni kwa x = 4, na 4 inavyoonekana katika bluu. Mstari unaofuata ni x + y = 5. Mstari unaofuata ni 4, umeonyeshwa kwa bluu + y = 5. Mstari unaofuata ni y = 1. Mstari wa mwisho ni “jozi iliyoamriwa 4, 1”.

    Tunaorodhesha pointi katika meza.

    x + y = 5
    x y (x, y)
    0 5 (0, 5)
    1 4 (1, 4)
    4 1 (4, 1)

    Kisha njama pointi, angalia kwamba wanaendelea, na kuteka mstari.

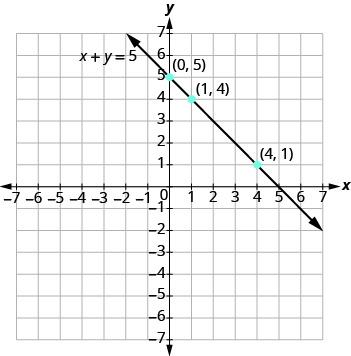
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. line hupita kwa njia ya pointi tatu labeled, “awali jozi 0, 5”, “awali jozi 1, 4", na kuamuru jozi 4, 1”. Mstari umeandikwa x + y = 5.

    Zoezi\(\PageIndex{6}\):

    Grafu equation: x + y = -2.

    Jibu

    Grafu hii ya jibu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Equation x plus y sawa na -2 inavyoonyeshwa. Mstari unapita kupitia intercepts na kuratibu 0, -2 na -2, 0.

    Zoezi\(\PageIndex{7}\):

    Grafu equation: x - y = 6.

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa 6, 0” na “jozi iliyoamriwa 0, -6".

    Katika mfano uliopita, pointi tatu tulizopata zilikuwa rahisi kwa grafu. Lakini hii si mara zote kesi. Hebu tuone nini kinatokea katika equation 2x + y = 3. Ikiwa y ni 0, ni thamani gani ya x?

    \[\begin{split} 2x + y &= 3 \\ 2x + \textcolor{red}{0} &= 3 \\ 2x &= 3 \\ x &= \dfrac{3}{2} \end{split}\]

    Suluhisho ni hatua\(\left(\dfrac{3}{2}, 0\right)\). Hatua hii ina sehemu ya x -kuratibu. Wakati tunaweza graph hatua hii, ni vigumu kuwa sahihi graphing FRACTIONS. Kumbuka katika mfano y =\(\dfrac{1}{2}\) x + 3, tulichagua kwa makini maadili kwa x ili tusipate sehemu ndogo kabisa. Ikiwa tunatatua equation 2x + y = 3 kwa y, itakuwa rahisi kupata ufumbuzi tatu kwa equation.

    \[\begin{split} 2x + y &= 3 \\ y &= -2x + 3 \end{split}\]

    Sasa tunaweza kuchagua maadili kwa x kwamba nitakupa kuratibu kwamba ni integers. Ufumbuzi wa x = 0, x = 1, na x = -1 huonyeshwa.

    y = -2x + 3
    x y (x, y)
    0 3 (0, 3)
    1 1 (1, 1)
    -1 5 (-1, 5)

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. line hupita kwa njia ya pointi tatu labeled, “awali jozi -1, 5", “awali jozi 0, 3", na kuamuru jozi 1, 1”. Mstari umeandikwa 2 x + y = 3.

    Mfano\(\PageIndex{5}\):

    Grafu equation 3x + y = -1.

    Suluhisho

    Pata pointi tatu ambazo ni ufumbuzi wa equation.

    Kwanza, tatua equation kwa y.

    \[\begin{split} 3x + y &= −1 \\ y &= −3x − 1 \end{split}\]

    Tutaweza basi x kuwa 0, 1, na -1 kupata pointi tatu. Jozi zilizoamriwa zinaonyeshwa kwenye meza. Panda pointi, angalia kwamba wanaendelea, na kuteka mstari.

    y = -3x - 1
    x y (x, y)
    0 -1 (0, -1)
    1 -4 (1, -4)
    -1 2 (-1, 2)

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -7 hadi 7. line hupita kwa njia ya pointi tatu labeled, “awali jozi -1, 2", “awali jozi 0, -1”, na kuamuru jozi 1, -4”. Mstari umeandikwa 3 x + y = -1.

    Ikiwa unaweza kuchagua pointi tatu za kuchora mstari, utajuaje ikiwa grafu yako inafanana na ile iliyoonyeshwa katika majibu katika kitabu? Ikiwa pointi ambapo grafu zinavuka x- na y -axes ni sawa, mechi ya grafu.

    Zoezi\(\PageIndex{8}\):

    Grafu kila equation: 2x + y = 2.

    Jibu
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. line hupita kwa njia ya pointi tatu labeled, “awali jozi -1, 4", “awali jozi 0, 2", na kuamuru jozi 1, 0”.
    Zoezi\(\PageIndex{9}\):

    Grafu kila equation: 4x + y = -3.

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x na y kila kukimbia kutoka -12 hadi 12. Mstari unapita kupitia pointi “jozi iliyoamriwa -2, 5" na “jozi iliyoamriwa 0, -3”.

    Wachangiaji na Attributi