10.10: Utangulizi wa Factoring Polynomials

Malengo ya kujifunza

• Pata sababu kubwa ya kawaida ya maneno mawili au zaidi
• Sababu kubwa ya kawaida sababu kutoka polynomial

kuwa tayari!

Kabla ya kuanza, fanya jaribio hili la utayari.

1. Sababu 56 katika primes. Ikiwa umekosa tatizo hili, kagua Mfano 2.9.1.
2. Panua: -3 (6a + 11). Ikiwa umekosa tatizo hili, kagua Mfano 7.4.9.
3. Kuzidisha: 4x ² (x ² + 3x - 1). Ikiwa umekosa tatizo hili, kagua Mfano 10.4.5.

Pata sababu kubwa ya kawaida ya maneno mawili au Zaidi

Mapema tuliongeza mambo pamoja ili kupata bidhaa. Sasa, tutabadilisha mchakato huu; tutaanza na bidhaa na kisha kuivunja ndani ya mambo yake. Kugawanyika bidhaa katika mambo inaitwa factoring.

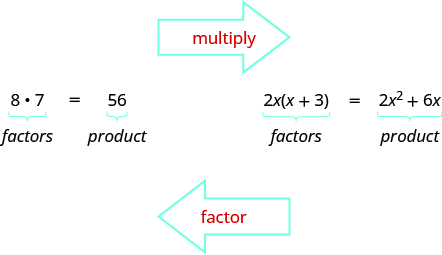
Katika lugha ya Algebra sisi factored idadi ya kupata angalau kawaida nyingi (LCM) ya namba mbili au zaidi. Sasa tutazingatia maneno na kupata sababu kubwa ya kawaida ya maneno mawili au zaidi. Njia tunayotumia ni sawa na kile tulichotumia kupata LCM.

Ufafanuzi: Sababu kuu ya kawaida

Sababu kubwa zaidi ya kawaida (GCF) ya maneno mawili au zaidi ni usemi mkubwa ambao ni sababu ya maneno yote.

Kwanza tutapata sababu kubwa ya kawaida ya namba mbili

Mfano$\PageIndex{1}$:

Kupata kubwa ya kawaida sababu ya 24 na 36.

Suluhisho

Hatua ya 1: Fanya kila mgawo katika primes. Andika vigezo vyote na vielelezo katika fomu iliyopanuliwa.	sababu 24 na 36.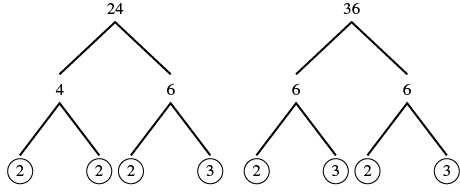
Hatua ya 2: Orodha ya mambo yote-vinavyolingana na mambo ya kawaida katika safu.
Katika kila safu, duru mambo ya kawaida.	Circle 2, 2, na 3 kwamba ni pamoja na idadi zote mbili.
Hatua ya 3: Kuleta mambo ya kawaida ambayo maneno yote hushiriki.	Kuleta chini 2, 2, 3 na kisha kuzidisha.
Hatua ya 4: Panua mambo.		GCF ya 24 na 36 ni 12.

Kumbuka kwamba tangu GCF ni sababu ya namba zote mbili, 24 na 36 zinaweza kuandikwa kama wingi wa 12.

$$\begin{split} 24 &= 12 \cdot 2 \\ 36 &= 12 \cdot 3 \end{split}$$

Zoezi$\PageIndex{1}$:

Kupata kubwa ya kawaida sababu: 54, 36.

Jibu

18

Zoezi$\PageIndex{2}$:

Kupata kubwa ya kawaida sababu: 48, 80.

Jibu

16

Katika mfano uliopita, tuligundua sababu kubwa ya kawaida ya mara kwa mara. Sababu kubwa ya kawaida ya kujieleza kwa algebraic inaweza kuwa na vigezo vilivyoinuliwa kwa nguvu pamoja na coefficients. Tunafupisha hatua tunazotumia ili kupata sababu kubwa zaidi ya kawaida.

JINSI YA: KUPATA SABABU KUBWA YA KAWAIDA

Hatua ya 1. Factor kila mgawo katika primes. Andika vigezo vyote na vielelezo katika fomu iliyopanuliwa.

Hatua ya 2. Orodha ya mambo yote-vinavyolingana mambo ya kawaida katika safu. Katika kila safu, duru mambo ya kawaida.

Hatua ya 3. Kuleta mambo ya kawaida ambayo maneno yote hushiriki.

Hatua ya 4. Panua mambo.

Mfano$\PageIndex{2}$:

Kupata kubwa ya kawaida sababu ya 5x na 15.

Suluhisho

Factor kila idadi katika primes. Circle mambo ya kawaida katika kila safu. Kuleta mambo ya kawaida.

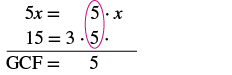GCF ya 5x na 15 ni 5.

Zoezi$\PageIndex{3}$:

Kupata kubwa ya kawaida sababu: 7y, 14.

Jibu

7

Zoezi$\PageIndex{4}$:

Kupata kubwa ya kawaida sababu: 22, 11m.

Jibu

11

Katika mifano hadi sasa, sababu kubwa ya kawaida ilikuwa mara kwa mara. Katika mifano miwili ijayo tutapata vigezo katika sababu kubwa ya kawaida.

Mfano$\PageIndex{3}$:

Kupata kubwa ya kawaida sababu ya 12x ² na 18x ³.

Suluhisho

Factor kila mgawo katika primes na kuandika vigezo na exponents katika fomu kupanua. Circle mambo ya kawaida katika kila safu. Kuleta mambo ya kawaida. Panua mambo.

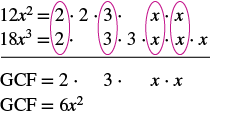GCF ya 12x ² na 18x ³ ni 6x ².

Zoezi$\PageIndex{5}$:

Kupata kubwa ya kawaida sababu: 16x ², 24x ³.

Jibu

$8x^2$

Zoezi$\PageIndex{6}$:

Kupata kubwa ya kawaida sababu: 27y ³, 18y ⁴.

Jibu

$9y^3$

Mfano$\PageIndex{4}$:

Kupata kubwa ya kawaida sababu ya 14x ³, 8x ², 10x.

Suluhisho

Factor kila mgawo katika primes na kuandika vigezo na exponents katika fomu kupanua. Circle mambo ya kawaida katika kila safu. Kuleta mambo ya kawaida. Panua mambo.

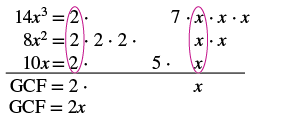GCF ya 14x ³ na 8x ², na 10x ni 2x.

Zoezi$\PageIndex{7}$:

Kupata kubwa ya kawaida sababu: 21x ³, 9x ², 15x.

Jibu

3x

Zoezi$\PageIndex{8}$:

Kupata kubwa ya kawaida sababu: 25m ⁴, 35m ³, 20m ².

Jibu

$5m^2$

Sababu ya Sababu kuu ya kawaida kutoka kwa Polynomial

Kama ilivyo katika hesabu, ambapo wakati mwingine ni muhimu kuwakilisha idadi katika fomu iliyosababishwa (kwa mfano, 12 kama 2 • 6 au 3 • 4), katika algebra inaweza kuwa na manufaa kuwakilisha polynomial katika fomu iliyopangwa. Njia moja ya kufanya hivyo ni kwa kutafuta sababu kubwa ya kawaida ya maneno yote. Kumbuka kwamba unaweza kuzidisha polynomial na monomial kama ifuatavyo:

$$\begin{split} 2(x &+ 7) \quad factors \\ 2 \cdot x &+ 2 \cdot 7 \\ 2x &+ 14 \quad product \end{split}$$

Hapa, tutaanza na bidhaa, kama 2x + 14, na kumaliza na mambo yake, 2 (x + 7). Ili kufanya hivyo tunatumia Mali ya Usambazaji “kwa reverse”.

Ufafanuzi: Mali ya Kusambaza

Ikiwa a, b, c ni namba halisi, basi (b + c) = ab + ac na ab + ac = a (b + c).

Fomu upande wa kushoto hutumiwa kuzidi. Fomu ya haki hutumiwa kuzingatia.

Hivyo ni jinsi gani sisi kutumia Mali Distributive kwa sababu polynomial? Tunapata GCF ya maneno yote na kuandika polynomial kama bidhaa!

Mfano$\PageIndex{5}$:

sababu: 2x + 14.

Suluhisho

Hatua ya 1: Pata GCF ya masharti yote ya polynomial.	Kupata GCF ya 2x na 14.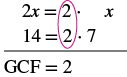
Hatua ya 2: Andika upya kila neno kama bidhaa kwa kutumia GCF.	Andika upya 2x na 14 kama bidhaa za GCF yao, 2. $$\ kuanza {kupasuliwa} 2x &= 2\ cdot x\\ 14 &= 2\ cdot 7\ mwisho {mgawanyiko}$$	$$\ kuanza {split} 2x & + 14\\ textcolor {nyekundu} {2}\ cdot x & +\ textcolor {nyekundu} {2}\ cdot 7\ mwisho {mgawanyiko}$$
Hatua ya 3: Tumia Mali ya Mgawanyo 'katika reverse' ili kuzingatia maneno.		2 (x + 7)
Hatua ya 4: Angalia kwa kuzidisha mambo.	Angalia.	$$\ kuanza {kupasuliwa} 2 (x &+ 7)\\ 2\ cdot x &+ 2\ cdot 7\\ 2x &+ 14\;\ checkmark\ mwisho {mgawanyiko}$$

Zoezi$\PageIndex{9}$:

sababu: 4x + 12.

Jibu

4 (x + 3)

Zoezi$\PageIndex{10}$:

sababu: 6a + 24.

Jibu

6 (a + 4)

Angalia kwamba katika Mfano 10.84, tulitumia neno sababu kama nomino na kitenzi:

nomino	7 ni sababu ya 14
Kitenzi	Sababu 2 kutoka 2x + 14

JINSI YA: SABABU YA SABABU KUBWA ZAIDI KUTOKA KWA POLYNOMIAL

Hatua ya 1. Pata GCF ya masharti yote ya polynomial.

Hatua ya 2. Andika upya kila neno kama bidhaa kwa kutumia GCF.

Hatua ya 3. Tumia Mali ya Distributive 'katika reverse' kwa sababu ya kujieleza.

Hatua ya 4. Angalia kwa kuzidisha mambo.

Mfano$\PageIndex{6}$:

sababu: 3a + 3.

Suluhisho

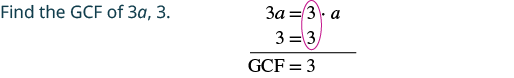Andika upya kila neno kama bidhaa kwa kutumia GCF.	$$\ textcolor {nyekundu} {3}\ cdot a +\ textcolor {nyekundu} {3}\ cdot$$
Tumia Mali ya Distributive 'katika reverse' kwa sababu GCF.	$3 (a+1) $$
Angalia kwa kuzidisha mambo ya kupata polynomial ya awali.	$$\ kuanza {kupasuliwa} 3 (a & + 1)\\ 3\ cdot &= 3\ cdot 1\\ 3a &+ 3\;\ checkmark\ mwisho {mgawanyiko}$$

Zoezi$\PageIndex{11}$:

sababu: 9a + 9.

Jibu

9 (a + 1)

Zoezi$\PageIndex{12}$:

sababu: 11x + 11.

Jibu

11 (x + 1)

Maneno katika mfano unaofuata yana mambo kadhaa kwa pamoja. Kumbuka kuandika GCF kama bidhaa ya mambo yote ya kawaida.

Mfano$\PageIndex{7}$:

sababu: 12x - 60.

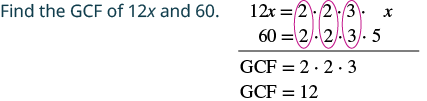Andika upya kila neno kama bidhaa kwa kutumia GCF.	$$\ textcolor {nyekundu} {12}\ cdot x -\ textcolor {nyekundu} {12}\ cdot $5
Sababu ya GCF.	$12 (x-5) $$
Angalia kwa kuzidisha mambo.	$$\ kuanza {mgawanyiko} 12 (x &- 5)\\ 12\ cdot x &- 12\ cdot 5\\ 12x &- 60\;\ checkmark\ mwisho {mgawanyiko}$$

Zoezi$\PageIndex{13}$:

sababu: 11x - 44.

Jibu

11 (x - 4)

Zoezi$\PageIndex{14}$:

sababu: 13y - 52.

Jibu

13 (y - 4)

Sasa tutazingatia sababu kubwa zaidi kutoka kwa trinomial. Tunaanza kwa kutafuta GCF ya masharti yote matatu.

Mfano$\PageIndex{8}$:

sababu: 3y ² + 6y + 9.

Suluhisho

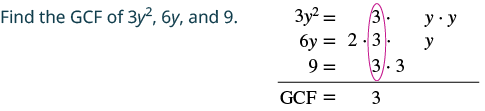Andika upya kila neno kama bidhaa kwa kutumia GCF.	$$\ textcolor {nyekundu} {3}\ cdot y ^ {2} +\ textcolor {nyekundu} {3}\ cdot 2y +\ textcolor {nyekundu} {3}\ cdot $3 $
Sababu ya GCF.	$3 (y^ {2} + 2y + 3) $$
Angalia kwa kuzidisha.	$$\ kuanza {kupasuliwa} 3 (y ^ {2} &+ 2y + 3)\\ 3\ cdot y ^ {2} &+ 3\ cdot 2y + 3\ cdot 3\\ 3y ^ {2} &+ 6y + 9\;\ alama\ mwisho {mgawanyiko}$$

Zoezi$\PageIndex{15}$:

sababu: 4y ² + 8y + 12.

Jibu

$4\left(y^{2}+2 y+3\right)$

Zoezi$\PageIndex{16}$:

sababu: 6x ² + 42x - 12.

Jibu

$6\left(x^{2}+7 x-2\right)$

Katika mfano unaofuata, sisi sababu variable kutoka binomial.

Mfano$\PageIndex{9}$:

sababu: 6x ² + 5x.

Suluhisho

Kupata GCF ya 6x ^2 na 5x na hesabu kwamba huenda na hayo.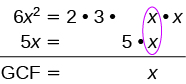
Andika upya kila neno kama bidhaa.	$$\ textcolor {nyekundu} {x}\ cdot 6x +\ textcolor {nyekundu} {x}\ cdot $5 $
Sababu ya GCF.	$$x (6x + 5)$$
Angalia kwa kuzidisha.	$$\ kuanza {mgawanyiko} x (6x &+ 5)\\ x\ cdot 6x &+ x\ cdot 5\\ 6x^ {2} &+ 5x\;\ checkmark\ mwisho {mgawanyiko}$$

Zoezi$\PageIndex{17}$:

sababu: 9x ² + 7x.

Jibu

$x(9x+7)$

Zoezi$\PageIndex{18}$:

sababu: 5a ² - 12a.

Jibu

(5a - 12)

Wakati kuna mambo kadhaa ya kawaida, kama tutakavyoona katika mifano miwili ijayo, shirika nzuri na kazi nzuri husaidia!

Mfano$\PageIndex{10}$:

sababu: 4x ³ - 20x ².

Suluhisho

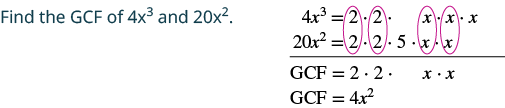Andika upya kila neno.	$$\ rangi ya maandishi {nyekundu} {4x^ {2}}\ cdot x -\ textcolor {nyekundu} {4x^ {2}}\ cdot $5
Sababu ya GCF.	$4x^ {2} (x-5) $$
Angalia.	$$\ kuanza {mgawanyiko} 4x^ {2} (x &- 5)\\ 4x^ {2}\ cdot x &- 4x^ {2}\ cdot 5\\ 4x^ {3} &- 20x^ {2}\;\ alama\ mwisho {mgawanyiko}$$

Zoezi$\PageIndex{19}$:

sababu: 2x ³ + 12x ².

Jibu

$2 x^{2}(x+6)$

Zoezi$\PageIndex{20}$:

sababu: 6y ³ - 15y ².

Jibu

$3 y^{2}(2 y-5)$

Mfano$\PageIndex{11}$:

sababu: 21y ² + 35y.

Suluhisho

Kupata GCF ya 21y ^2 na 35y.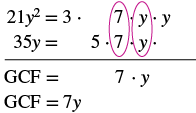
Andika upya kila neno.	$$\ textcolor {nyekundu} {7y}\ cdot 3y +\ textcolor {nyekundu} {7y}\ cdot $5 $
Sababu ya GCF.	$7y (3y + 5) $$

Zoezi$\PageIndex{21}$:

sababu: 18y ² + 63y.

Jibu

9 (2y + 7)

Zoezi$\PageIndex{22}$:

sababu: 32k ² + 56k.

Jibu

8k (4k + 7)

Mfano$\PageIndex{12}$:

sababu: 14x ³ + 8x ² ÷ 10x.

Suluhisho

Hapo awali, tuligundua GCF ya 14x ³, 8x ², na 10x kuwa 2x.

Andika upya kila neno kwa kutumia GCF, 2x.	$$\ rangi ya maandishi {nyekundu} {2x}\ cdot 7x^ {2} +\ rangi ya maandishi {nyekundu} {2x}\ cdot 4x -\ textcolor {nyekundu} {2x}\ cdot $5
Sababu ya GCF.	$2x (7x^ {2} + 4x - 5) $$
Angalia.	$$\ kuanza {kupasuliwa} 2x (7x^ {2} &+ 4x - 5)\\ 2x\ cdot 7x^ {2} &+ 2x\ cdot 4x - 2x\ cdot 5\\ 14x^ {3} &+ 8x^ {2} - 10x\;\ alama\ mwisho {mgawanyiko}$$

Zoezi$\PageIndex{23}$:

Sababu: 18y ³ - 6y ² - 24y.

Jibu

$6 y\left(3 y^{2}-y-4\right)$

Zoezi$\PageIndex{24}$:

sababu: 16x ³ + 8x ² ÷ 12x.

Jibu

$4 x\left(4 x^{2}+2 x-3\right)$

Wakati mgawo wa kuongoza, mgawo wa muda wa kwanza, ni hasi, tunaona hasi kama sehemu ya GCF.

Mfano$\PageIndex{13}$:

Sababu: -9y - 27.

Suluhisho

Wakati mgawo wa kuongoza ni hasi, GCF itakuwa hasi. Kupuuza ishara za maneno, sisi kwanza kupata GCF ya 9y na 27 ni 9.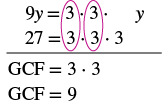
Kwa kuwa maneno -9y - 27 ina mgawo wa kuongoza hasi, tunatumia -9 kama GCF.
Andika upya kila neno kwa kutumia GCF.	$$\ rangi ya maandishi {nyekundu} {-9}\ cdot y + (\ textcolor {nyekundu} {-9})\ cdot $3 $
Sababu ya GCF.	$-9 (y+3) $$
Angalia.	$$\ kuanza {mgawanyiko} -9 (y &+ 3)\\ -9\ cdot y &+ (-9)\ cdot 3\\ -9y &- 27\;\ checkmark\ mwisho {mgawanyiko}$$

Zoezi$\PageIndex{25}$:

Sababu: -5y - 35.

Jibu

-5 (y + 7)

Zoezi$\PageIndex{26}$:

Sababu: -16z - 56.

Jibu

-8 (2z + 7)

Jihadharini sana na ishara za maneno katika mfano unaofuata.

Mfano$\PageIndex{14}$:

Sababu: -4a ² + 16a.

Suluhisho

Mgawo wa kuongoza ni hasi, hivyo GCF itakuwa hasi.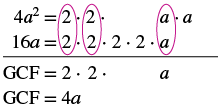
Kwa kuwa mgawo wa kuongoza ni hasi, GCF ni hasi, -4a.
Andika upya kila neno.	$$\ textcolor {nyekundu} {-4a}\ cdot a - (\ textcolor {nyekundu} {-4a})\ cdot $4 $
Sababu ya GCF.	$-4a (a-4) $$
Angalia mwenyewe kwa kuzidisha.

Zoezi$\PageIndex{27}$:

Sababu: -7a ² + 21a.

Jibu

-7a (a - 3)

Zoezi$\PageIndex{28}$:

Sababu: -6x ² + x.

Jibu

-x (6x - 1)

PATA RASILIMALI ZA ZIADA

Factor GCF

Sababu ya Binomial

Tambua GCF

Mazoezi hufanya kamili

Pata sababu kubwa ya kawaida ya maneno mawili au Zaidi

Katika mazoezi yafuatayo, pata sababu kubwa zaidi ya kawaida.

422. 40, 56
423. 45, 75
424. 72, 162
425. 150, 275
426. 3x, 12
427. 4y, 28
428. 10a, 50
429. 5b, 30
430. 16y, 24y ²
431. 9x, 15x ²
432. 18m ³, 36m ²
433. 12p ⁴, 48p ³
434. 10x, 25x ², 15x ³
435. 18a, 6a ², 22a ³
436. 24u, 6u ², 30u ³
437. 40y, 10y ², 90y ³
438. 15a ⁴, 9a ⁵, 21a ⁶
439. 35x ³, 10x ⁴, 5x ⁵
440. 27y ², 45y ³, 9y ⁴
441. 14b ², 35b ³, 63b ⁴

Sababu ya Sababu kuu ya kawaida kutoka kwa Polynomial

Katika mazoezi yafuatayo, fikiria sababu kubwa zaidi kutoka kwa kila polynomial.

442. 2x 8
443. 5y + 15
444. 3a - 24
445. 4b - 20
446. 9 - 9
447. 7x - 7
448. 5m ² + 20m + 35
449. 3n ² + 21n + 12
450. 8p ² + 32p + 48
451. 6q ² + 30q + 42
452. 8q ² + 15q
453. 9c ² + 22c
454. 13k ² + 5k
455. 17x ² + 7x
456. 5c ² + 9c
457. 4q ² + 7q
458. 5p ² + 25p
459. 3r ² + 27r
460. 24q ² - 12q
461. 30u ² - 10u
462. yz + 4z
463. ab + 8b
464. 60x - 6x ³
465. 55y - 11y ⁴
466. 48r ⁴ - 12r ³
467. 45c ³ - 15c ²
468. 4a ³ - 4ab ²
469. 6c ³ - 6cd ²
470. 30u ³ + 80u ²
471. 48x ³ + 72x ²
472. 120y ⁶ + 48y ⁴
473. 144a ⁶ + 90a ³
474. 4q ² + 24q + 28
475. 10y ² + 50y + 40
476. 15z ² - 30z - 90
477. 12u ² - 36u - 108
478. 3a ⁴ - 24a ³ + 18a ²
479. 5p ⁴ - 20p ³ - 15p ²
480. 11x ⁶ + 44x ⁵ - 121x ⁴
481. 8c ⁵ + 40c ⁴ - 56c ³
482. —3n - 24
483. -7p - 84
484. -15a ² - 40a
485. -18b ² - 66b
486. -10y ³ + 60y ²
487. -8a ³ + 32a ²
488. -4u ⁵ + 56u ³
489. -9b ⁵ + 63b ³

kila siku Math

490. Mapato Mtengenezaji wa sehemu zote za microwave amegundua kwamba mapato yaliyopatikana kutokana na kuuza microwaves gharama ya dola p kila mmoja hutolewa na polynomial -5p ² + 150p. Sababu ya sababu kubwa zaidi kutoka kwa polynomial hii.
491. Urefu wa baseball Urefu wa baseball hit na kasi 80 miguuu/pili katika 4 miguu juu ya usawa wa ardhi ni -16t ² + 80t + 4, na t = idadi ya sekunde tangu ilipigwa. Sababu ya sababu kubwa zaidi kutoka kwa polynomial hii.

Mazoezi ya kuandika

492. Sababu kubwa ya kawaida ya 36 na 60 ni 12. Eleza nini hii inamaanisha.
493. GCF ya y ⁴, y ⁵, na y ¹⁰ ni nini? Andika kanuni ya jumla inayoelezea jinsi ya kupata GCF ya y ^a, y ^b, na y ^c.

Self Check

(a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

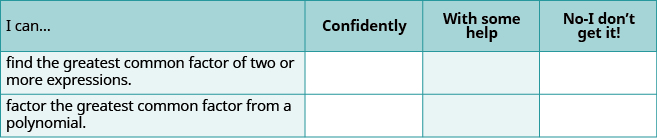
(b) Kwa ujumla, baada ya kuangalia orodha, unafikiri wewe ni vizuri tayari kwa ajili ya Sura ya? Kwa nini au kwa nini?

Wachangiaji na Majina

• Template:ContribOpenStaxPreAlgebra