10.S: Polynomials (muhtasari)

Masharti muhimu

binomial	Polynomial na maneno mawili hasa
shahada ya mara kwa mara	Kiwango cha mara kwa mara ni 0.
shahada ya polynomial	Kiwango cha polynomial ni kiwango cha juu cha masharti yake yote.
shahada ya muda	Kiwango cha muda wa polynomial ni kielelezo cha kutofautiana kwake.
sababu kubwa ya kawaida	Sababu kubwa zaidi ya kawaida (GCF) ya maneno mawili au zaidi ni usemi mkubwa ambao ni sababu ya maneno yote.
monomial	Neno la shaba la fomu ^m, ambapo a ni mara kwa mara na m ni namba nzima, inaitwa monomial.
mtetezi hasi	Ikiwa n ni integer chanya na ≥ 0, basi\(a^{-n} = \dfrac{1}{a^{n}}\).
polynomial	Polynomial ni monomial, au monomials mbili au zaidi, pamoja na kuongeza au kuondoa.
nukuu ya kisayansi	Idadi walionyesha katika nukuu ya kisayansi wakati ni ya fomu a × 10 ^n, ambapo ≥ 1 na a <10, na n ni integer.
ya trinomial	Trinomial ni polynomial na maneno matatu hasa.
sifuri exponent	Ikiwa ni nambari isiyo ya sifuri, basi ^0 = 1. Nambari yoyote isiyo ya zero iliyoinuliwa kwa nguvu ya sifuri ni 1.

Dhana muhimu

10.2 - Tumia Mali ya kuzidisha ya Watazamaji

• Nukuu ya kielelezo

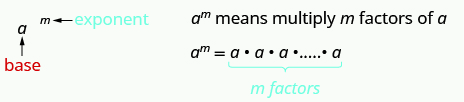
Hii ni kusoma kwa m ^th nguvu.

• Bidhaa Mali ya Watazamaji
  • Ikiwa ni namba halisi na m, n ni kuhesabu namba, basi ^m • ⁿ = ^{m + n}
  • Ili kuzidisha na besi kama, ongeza vielelezo.
• Mali ya Nguvu kwa Watazamaji
  • Ikiwa ni namba halisi na m, n ni kuhesabu namba, basi (^m) ⁿ = ^{m • n}
• Bidhaa kwa Mali ya Nguvu kwa Watazamaji
  • Ikiwa a na b ni namba halisi na m ni namba nzima, basi (ab) ^m = ^m b ^m

10.3 - Kuzidisha Polynomials

• Tumia njia ya FOIL ya kuzidisha binomials mbili.

Hatua ya 1. Panua maneno ya kwanza.
Hatua ya 2. Panua maneno ya nje.
Hatua ya 3. Panua maneno ya ndani.
Hatua ya 4. Kuzidisha maneno ya mwisho.
Hatua ya 5. Kuchanganya kama maneno, wakati iwezekanavyo.

• Kuzidisha Binomials mbili: Ili kuzidisha binomials, tumia:
  • Mali ya Kusambaza
  • Njia ya foil
  • Njia ya wima
• Kuzidisha Trinomial na Binomial: Ili kuzidisha trinomial na binomial, tumia:
  • Mali ya Kusambaza
  • Njia ya wima

10.4 - Gawanya Monomials

• Sawa FRACTIONS Mali
  • Kama, b, c ni namba nzima ambapo b 坪 0, c 坪 0, kisha $$\ dfrac {a} {b} =\ dfrac {a\ cdot c} {b\ cdot c}\ quad na\ quad\ dfrac {a\ cdot c} {b\ cdot c} =\ dfrac {a} {b} $$
• sifuri exponent
  • Ikiwa ni nambari isiyo ya sifuri, basi ⁰ = 1.
  • Nambari yoyote isiyo ya zero iliyoinuliwa kwa nguvu ya sifuri ni 1.
• Mali ya Quotient kwa Watazamaji
  • Ikiwa ni namba halisi, a 坪 0, na m, n ni namba nzima, kisha $$\ dfrac {a^ {m}} {a^ {n}} = a^ {m-n},\; m>n\ quad na\ quad\ dfrac {a^ {m} {a^ {m} {a^ {n-m}},\; n>m $$
• Quotient kwa Mali Nguvu kwa Watazamaji
  • Ikiwa a na b ni namba halisi, b 坪 0, na m ni namba ya kuhesabu, basi $$\ kushoto (\ dfrac {a} {b}\ haki) ^ {m} =\ dfrac {a^ {m}} {b ^ {m}} $$
  • Ili kuongeza sehemu kwa nguvu, ongeza nambari na denominator kwa nguvu hiyo.

10.5 - Integer Exponents na Nukuu ya kisayansi

• Muhtasari wa Mali Exponent
  • Ikiwa a, b ni namba halisi na m, n ni integers, basi

Bidhaa Mali	^m • ^n = ^m + n
Power Mali	(^m) ^n = ^m • n
Bidhaa kwa Mali ya Nguvu	(ab) ^m = ^m b ^m
Mali ya Quotient	\(\dfrac{a^{m}}{a^{n}}\)= ^m - n, a - 0, m> n
	\(\dfrac{a^{m}}{a^{n}} = \dfrac{1}{a^{n-m}}\), a - 0,0, n> m
Zero Exponent Mali	a ^0 = 1, a ∙ 0
Quotient kwa Mali Nguvu	\(\left(\dfrac{a}{b}\right)^{m} = \dfrac{a^{m}}{b^{m}}\), b ∙ 0
Ufafanuzi wa Exponent Hasi	\(a^{-n} = \dfrac{1}{a^{n}}\)

• Badilisha kutoka Nukuu ya Decimal hadi Notation ya Sayansi: Ili kubadilisha decimal kwa notation ya kisayansi:
  1. Hoja uhakika decimal ili sababu ya kwanza ni kubwa kuliko au sawa na 1 lakini chini ya 10.
  2. Hesabu idadi ya maeneo ya decimal, n, kwamba hatua ya decimal ilihamishwa. Andika namba kama bidhaa yenye nguvu ya 10.
     • Ikiwa idadi ya awali ni kubwa kuliko 1, nguvu ya 10 itakuwa 10 ⁿ.
     • Ikiwa nambari ya awali ni kati ya 0 na 1, nguvu ya 10 itakuwa 10 ⁿ.
  3. Angalia.
• Badilisha Nukuu ya kisayansi kwa Fomu ya Decimal: Ili kubadilisha notation ya kisayansi kwa fomu ya decimal
  1. Kuamua exponent, n, juu ya sababu 10.
  2. Hoja decimal n maeneo, kuongeza zero kama inahitajika.
     • Kama exponent ni chanya, hoja uhakika decimal n maeneo ya haki.
     • Kama exponent ni hasi, hoja uhakika decimal |n| maeneo ya kushoto.
  3. Angalia.

10.6 - Utangulizi wa Factoring Polynomials

• Pata sababu kubwa zaidi.
  1. Factor kila mgawo katika primes. Andika vigezo vyote na vielelezo katika fomu iliyopanuliwa.
  2. Orodha ya mambo yote-vinavyolingana mambo ya kawaida katika safu. Katika kila safu, duru mambo ya kawaida.
  3. Kuleta mambo ya kawaida ambayo maneno yote hushiriki.
  4. Panua mambo.
• Mali ya Kusambaza
  • Ikiwa a, b, c ni namba halisi, basi (b + c) = ab + ac na ab + ac = a (b + c).
• Sababu ya sababu kubwa zaidi kutoka kwa polynomial.
  1. Pata GCF ya masharti yote ya polynomial.
  2. Andika upya kila neno kama bidhaa kwa kutumia GCF.
  3. Tumia Mali ya Distributive 'katika reverse' kwa sababu ya kujieleza.
  4. Angalia kwa kuzidisha mambo.

Wachangiaji na Majina

• Template:ContribOpenStaxPreAlgebra