Skip to main content
Global

10.4: Kuzidisha Polynomials (Sehemu ya 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    173418

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Kuzidisha polynomial na monomial
    • Panua binomial kwa binomial
    • Panua trinomial na binomial
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kusambaza: 2 (x + 3). Ikiwa umekosa tatizo, kagua Mfano 7.4.1.
    2. Kusambaza: -11 (4 - 3a). Ikiwa umekosa tatizo, tathmini Mfano 7.4.10.
    3. Kuchanganya kama maneno: x 2 + 9x + 7x + 63. Ikiwa umekosa tatizo, kagua Mfano 2.3.9.

    Kuzidisha Polynomial na Monomial

    Katika Mali ya Kusambaza ulijifunza kutumia Mali ya Usambazaji ili kurahisisha maneno kama vile 2 (x -3). Umeongeza maneno yote katika mabano, x na 3, na 2, ili kupata 2x - 6. Kwa msamiati mpya wa sura hii, unaweza kusema ulikuwa unazidisha binomial, x - 3, na monomial, 2. Kuzidisha binomial kwa monomial si kitu kipya kwako!

    Mfano\(\PageIndex{1}\):

    Panua: 3 (x + 7).

    Suluhisho

    Kusambaza. 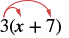CNX_BMath_Figure_10_03_001_img-01.png
      3 • x + 3 • 7
    Kurahisisha. 3x 21
    Zoezi\(\PageIndex{1}\):

    Panua: 6 (x + 8).

    Jibu

    6x 48

    Zoezi\(\PageIndex{2}\):

    Panua: 2 (y + 12).

    Jibu

    2y + 24

    Mfano\(\PageIndex{2}\):

    Panua: x (x - 8).

    Suluhisho

    Kusambaza. 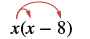CNX_BMath_Figure_10_03_044_img-01.png
      x 2 - 8x
    Kurahisisha. x 2 - 8x
    Zoezi\(\PageIndex{3}\):

    Ongeza: y (y - 9).

    Jibu

    \( y^{2}-9 y\)

    Zoezi\(\PageIndex{4}\):

    Panua: (p - 13).

    Jibu

    \( p^2 - 13p\)

    Mfano\(\PageIndex{3}\):

    Kuzidisha: 10x (4x + y).

    Suluhisho

    Kusambaza. 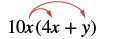CNX_BMath_Figure_10_03_045_img-02.png
      10x • 4x + 10x • y
    Kurahisisha. 40x 2 + 10xy
    Zoezi\(\PageIndex{5}\):

    Kuzidisha: 8x (x + 3y).

    Jibu

    \(8x^2+24xy \)

    Zoezi\(\PageIndex{6}\):

    Panua: 3r (6r + s).

    Jibu

    \(18r^2+3rs \)

    Kuzidisha monomial kwa kazi ya trinomial kwa njia sawa.

    Mfano\(\PageIndex{4}\):

    Kuzidisha: -2x (5x 2 + 7x - 3).

    Suluhisho

    Kusambaza. CNX_BMath_Figure_10_03_046_img-01.png
      -2x • 5x 2 + (-2x) • 7x - (-2x) • 3
    Kurahisisha. -10x 3 -14x 2 + 6x
    Zoezi\(\PageIndex{7}\):

    Panua: -4y (8y 2 + 5y - 9).

    Jibu

    \(-32y^3-20y^2+36y \)

    Zoezi\(\PageIndex{8}\):

    Kuzidisha: -6x (9x 2 + x - 1).

    Jibu

    \( -54x^3-6x^2+6x\)

    Mfano\(\PageIndex{5}\):

    Kuzidisha: 4y 3 (y 2 - 8y + 1).

    Suluhisho

    Kusambaza. 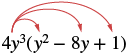CNX_BMath_Figure_10_03_047_img-01.png
      4y 3 • y 2 - 4y 3 • 8y + 4y 3 • 1
    Kurahisisha. 4y 5 -32y 4 + 4y 3
    Zoezi\(\PageIndex{9}\):

    Kuzidisha: 3x 2 (4x 2 - 3x + 9).

    Jibu

    \( 12 x^{4}-9 x^{3}+27 x^{2}\)

    Zoezi\(\PageIndex{10}\):

    Kuzidisha: 8y 2 (3y 2 - 2y - 4).

    Jibu

    \(24 y^{4}-16 y^{3}-32 y^{2} \)

    Sasa tutakuwa na monomial kama sababu ya pili.

    Mfano\(\PageIndex{6}\):

    Panua: (x + 3) p.

    Suluhisho

    Kusambaza. 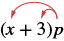CNX_BMath_Figure_10_03_048_img-01.png
      x • p + 3 • p
    Kurahisisha. xp + 3p
    Zoezi\(\PageIndex{11}\):

    Panua: (x + 8) p.

    Jibu

    \(xp+8p \)

    Zoezi\(\PageIndex{12}\):

    Panua: (a + 4) p.

    Jibu

    \(ap + 4p \)

    Kuzidisha Binomial na Binomial

    Kama kuna njia tofauti za kuwakilisha kuzidisha kwa idadi, kuna mbinu kadhaa ambazo zinaweza kutumika kuzidisha mara binomial binomial.

    Kutumia Mali ya Kusambaza

    Tutaanza kwa kutumia Mali ya Usambazaji. Angalia tena Mfano\(\PageIndex{6}\).

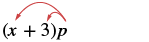      CNX_BMath_Figure_10_03_049_img-01.png
    Sisi kusambaza p kupata CNX_BMath_Figure_10_03_049_img-02.png
    Nini kama tuna (x + 7) badala ya p? Fikiria (x + 7) kama\(\textcolor{red}{p}\) hapo juu. 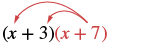CNX_BMath_Figure_10_03_049_img-03.png
    Kusambaza (x + 7). 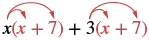CNX_BMath_Figure_10_03_049_img-04.png
    Kusambaza tena. x 2 + 7x + 3x + 21
    Kuchanganya kama maneno. x 2 + 10x + 21

    Angalia kwamba kabla ya kuchanganya maneno kama hayo, tulikuwa na maneno manne. Sisi kuzidisha masharti mawili ya binomial kwanza na masharti mawili ya pili binomial - nne kuzidisha.

    Kuwa makini kutofautisha kati ya jumla na bidhaa.

    \[\begin{split} &\textbf{Sum} \qquad \qquad \qquad \quad \textbf{Product} \\ &x + x \qquad \qquad \qquad \qquad x \cdot x \\ &\; \; 2x \qquad \qquad \qquad \qquad \qquad x^{2} \\ combine\; &like\; terms \qquad add\; exponents\; of\; like\; bases \end{split}\]

    Mfano\(\PageIndex{7}\):

    Panua: (x + 6) (x + 8).

    Suluhisho

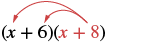      CNX_BMath_Figure_10_03_050_img-01.png
    Kusambaza (x + 8). 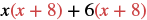CNX_BMath_Figure_10_03_050_img-02.png
    Kusambaza tena. x 2 + 8x + 6x + 48
    Kurahisisha. x 2 + 14x + 48
    Zoezi\(\PageIndex{13}\):

    Panua: (x + 8) (x + 9).

    Jibu

    \(x^{2}+17 x+72 \)

    Zoezi\(\PageIndex{14}\):

    Panua: (a + 4) (a + 5).

    Jibu

    \(a^{2}+9 a+20 \)

    Sasa tutaona jinsi ya kuzidisha binomials ambapo variable ina mgawo.

    Mfano\(\PageIndex{8}\):

    Panua: (2x + 9) (3x + 4).

    Suluhisho

    Kusambaza (3x + 4). 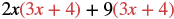CNX_BMath_Figure_10_03_051_img-01.png
    Kusambaza tena. 6x 2 + 8x + 27x 36
    Kurahisisha. 6x 2 + 35x + 36
    Zoezi\(\PageIndex{15}\):

    Panua: (5x + 9) (4x + 3).

    Jibu

    \(20 x^{2}+51 x+27 \)

    Zoezi\(\PageIndex{16}\):

    Panua: (10m + 9) (8m + 7).

    Jibu

    \(80 m^{2}+142 m+63 \)

    Katika mifano ya awali, binomials walikuwa kiasi. Wakati kuna tofauti, tunalipa kipaumbele maalum ili kuhakikisha ishara za bidhaa ni sahihi.

    Mfano\(\PageIndex{9}\):

    Panua: (4y + 3) (6y - 5).

    Suluhisho

    Kusambaza. 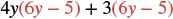CNX_BMath_Figure_10_03_052_img-01.png
    Kusambaza tena. 24y 2 - 20y + 18y - 15
    Kurahisisha. 24y 2 - 2y - 15
    Zoezi\(\PageIndex{17}\):

    Panua: (7y + 1) (8y - 3).

    Jibu

    \( 56 y^{2}-13 y-3\)

    Zoezi\(\PageIndex{18}\):

    Kuzidisha: (3x + 2) (5x - 8).

    Jibu

    \(15 x^{2}-14 x-16 \)

    Hadi kufikia hatua hii, bidhaa ya binomials mbili imekuwa trinomial. Hii si mara zote kesi.

    Mfano\(\PageIndex{10}\):

    Panua: (x + 2) (x - y).

    Suluhisho

    Kusambaza. 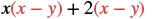CNX_BMath_Figure_10_03_053_img-02.png
    Kusambaza tena. x 2 - xy + 2x - 2y
    Kurahisisha. Hakuna maneno kama hayo ya kuchanganya.
    Zoezi\(\PageIndex{19}\):

    Panua: (x + 5) (x - y).

    Jibu

    \( x^{2}-x y+5 x-5 y\)

    Zoezi\(\PageIndex{20}\):

    Panua: (x + 2y) (x - 1).

    Jibu

    \( x^{2}-x+2 x y-2 y\)

    Wachangiaji na Majina