Skip to main content
Global

10.5: Kuzidisha Polynomials (Sehemu ya 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    173422

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Kutumia Njia ya FOIL

    Kumbuka kwamba unapozidisha binomial kwa binomial unapata maneno manne. Wakati mwingine unaweza kuchanganya kama maneno ili kupata trinomial, lakini wakati mwingine hakuna maneno kama ya kuchanganya. Hebu tuangalie mfano wa mwisho tena na uangalie hasa jinsi tulivyopata masharti manne.

    \[\begin{split} (x + 2)&(x - y) \\ x^{2} - xy &+ 2x - 2y \end{split}\]

    Je! Muda wa kwanza, x 2, unatoka wapi?

    Ni bidhaa ya x na x, maneno ya kwanza katika (x + 2) na (x - y).

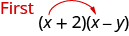
    Mabano x pamoja mara 2 mabano x minus y inavyoonekana. Kuna mshale nyekundu kutoka x ya kwanza hadi ya pili. Mbali na hili, “Kwanza” imeandikwa kwa nyekundu.

    Neno linalofuata, -xy, ni bidhaa ya x na -y, maneno mawili ya nje.

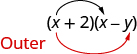
    Mabano x pamoja mara 2 mabano x minus y inavyoonekana. Kuna mshale mweusi kutoka x ya kwanza hadi x ya pili Kuna mshale mwekuNDU kutoka x kwanza hadi y Kando ya hili, “Nje” imeandikwa kwa nyekundu.

    Muda wa tatu, +2x, ni bidhaa ya 2 na x, maneno mawili ya ndani.

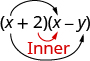
    Mabano x pamoja mara 2 mabano x minus y inavyoonekana. Kuna mshale mweusi kutoka x ya kwanza hadi x ya pili Kuna mshale mweusi kutoka x kwanza hadi y Kuna mshale mweusi kutoka kwa 2 hadi x. chini ya hapo, “Inner” imeandikwa kwa nyekundu.

    Na muda wa mwisho, -2y, ulitoka kuzidisha masharti mawili ya mwisho.

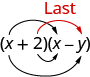
    Mabano x pamoja mara 2 mabano x minus y inavyoonekana. Kuna mshale mweusi kutoka x ya kwanza hadi x ya pili Kuna mshale mweusi kutoka x kwanza hadi y Kuna mshale mweusi kutoka 2 hadi x Kuna mshale mweusi kutoka 2 hadi y. hapo, “Mwisho” imeandikwa kwa nyekundu.

    Tunafupisha “Kwanza, Nje, Ndani, Mwisho” kama FOIL. Barua zinasimama kwa 'Kwanza, Nje, Ndani, Mwisho'. Neno FOIL ni rahisi kukumbuka na kuhakikisha tunapata bidhaa zote nne. Tunaweza kusema tunatumia njia ya FOIL kuzidisha binomials mbili.

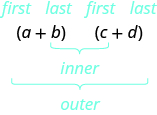
    Mabano pamoja b mara mabano c pamoja d inavyoonekana. Juu ya a ni ya kwanza, juu b ni ya mwisho, juu c ni ya kwanza, juu ya d ni ya mwisho. Kuna brace kuunganisha na d kwamba anasema nje. Kuna brace kuunganisha b na c kwamba anasema ndani.

    Hebu tuangalie (x + 3) (x + 7) tena. Sasa tutafanya kazi kupitia mfano ambapo tunatumia muundo wa FOIL kuzidisha binomials mbili.

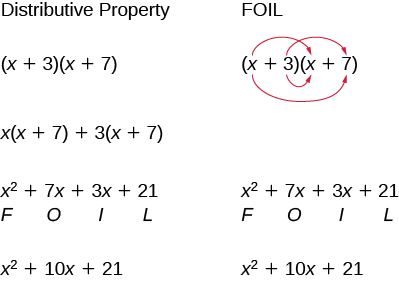
    CNX_BMath_Figure_10_03_063_img.jpg

    Mfano\(\PageIndex{11}\):

    Panua kutumia njia ya FOIL: (x + 6) (x + 9).

    Suluhisho

    Hatua ya 1: Panua maneno ya kwanza. 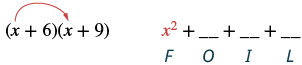CNX_BMath_Figure_10_03_054_img-01.png
    Hatua ya 2: Panua maneno ya nje. 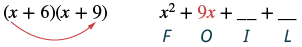CNX_BMath_Figure_10_03_054_img-02.png
    Hatua ya 3: Panua maneno ya ndani. 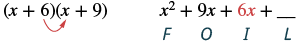CNX_BMath_Figure_10_03_054_img-03.png
    Hatua ya 4: Panua maneno ya mwisho. 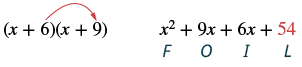CNX_BMath_Figure_10_03_054_img-04.png
    Hatua ya 5: Kuchanganya kama maneno, iwezekanavyo. x 2 + 15x + 54
    Zoezi\(\PageIndex{21}\):

    Panua kutumia njia ya FOIL: (x + 7) (x + 8).

    Jibu

    \(x^2+15x+56 \)

    Zoezi\(\PageIndex{22}\):

    Panua kutumia njia ya FOIL: (y + 14) (y + 2).

    Jibu

    \(y^2+16y+28\)

    Sisi muhtasari hatua za njia ya FOIL hapa chini. Njia ya FOIL inatumika tu kwa kuzidisha binomials, sio polynomials nyingine!

    JINSI YA: TUMIA NJIA YA FOIL KWA KUZIDISHA BINOMIALS MBILI

    Hatua ya 1. Panua maneno ya kwanza.

    Hatua ya 2. Panua maneno ya nje.

    Hatua ya 3. Panua maneno ya ndani.

    Hatua ya 4. Kuzidisha maneno ya mwisho.

    Hatua ya 5. Kuchanganya kama maneno, wakati iwezekanavyo.

    Mabano pamoja b mara mabano c pamoja d inavyoonekana. Juu ya a ni ya kwanza, juu b ni ya mwisho, juu c ni ya kwanza, juu ya d ni ya mwisho. Kuna brace kuunganisha na d kwamba anasema nje. Kuna brace kuunganisha b na c kwamba anasema ndani.

    Mfano\(\PageIndex{12}\):

    Panua: (y - 8) (y + 6).

    Suluhisho

    Hatua ya 1: Panua maneno ya kwanza. 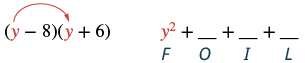CNX_BMath_Figure_10_03_055_img-01.png
    Hatua ya 2: Panua maneno ya nje. 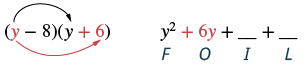CNX_BMath_Figure_10_03_055_img-02.png
    Hatua ya 3: Panua maneno ya ndani. 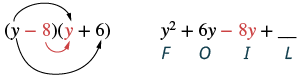CNX_BMath_Figure_10_03_055_img-03.png
    Hatua ya 4: Panua maneno ya mwisho. 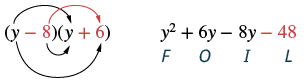CNX_BMath_Figure_10_03_055_img-04.png
    Hatua ya 5: Kuchanganya kama maneno, iwezekanavyo. y 2 - 2y - 48
    Zoezi\(\PageIndex{23}\):

    Panua: (y - 3) (y + 8).

    Jibu

    \(y^2+5y-24 \)

    Zoezi\(\PageIndex{24}\):

    Panua: (q - 4) (q + 5).

    Jibu

    \(q^2+q-20 \)

    Mfano\(\PageIndex{13}\):

    Kuzidisha: (2a + 3) (3a - 1).

    Suluhisho

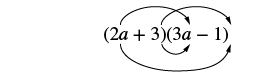      CNX_BMath_Figure_10_03_056_img-02.png
    Panua maneno ya kwanza. 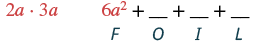CNX_BMath_Figure_10_03_056_img-03.png
    Panua maneno ya nje. 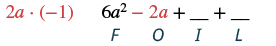CNX_BMath_Figure_10_03_056_img-04.png
    Panua maneno ya ndani. 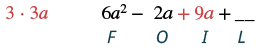CNX_BMath_Figure_10_03_056_img-05.png
    Kuzidisha maneno ya mwisho. 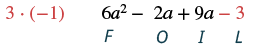CNX_BMath_Figure_10_03_056_img-06.png
    Kuchanganya kama maneno. 6a 2 + 7a - 3
    Zoezi\(\PageIndex{25}\):

    Panua: (4a + 9) (5a - 2).

    Jibu

    \(20a^2+37a-18 \)

    Zoezi\(\PageIndex{26}\):

    Kuzidisha: (7x + 4) (7x - 8).

    Jibu

    \( 49x^2-28x-32\)

    Mfano\(\PageIndex{14}\):

    Panua: (5x - y) (2x - 7).

    Suluhisho

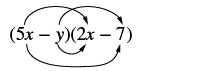      CNX_BMath_Figure_10_03_057_img-02.png
    Panua maneno ya kwanza. 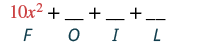CNX_BMath_Figure_10_03_057_img-03.png
    Panua maneno ya nje. 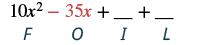CNX_BMath_Figure_10_03_057_img-04.png
    Panua maneno ya ndani. 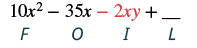CNX_BMath_Figure_10_03_057_img-05.png
    Kuzidisha maneno ya mwisho. 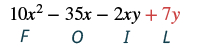CNX_BMath_Figure_10_03_057_img-06.png
    Kuchanganya kama maneno. Hakuna. 10x 2 - 35x - 2xy + 7y
    Zoezi\(\PageIndex{27}\):

    Panua: (12x - y) (x - 5).

    Jibu

    \(12 x^{2}-60 x-x y+5 y \)

    Zoezi\(\PageIndex{28}\):

    Kuzidisha: (6a - b) (2a - 9).

    Jibu

    \(12 a^{2}-54 a-2 a b+9 b \)

    Kutumia Njia ya Wima

    Njia ya FOIL ni kawaida njia ya haraka zaidi ya kuzidisha binomials mbili, lakini inafanya kazi tu kwa binomials. Unaweza kutumia Mali Distributive kupata bidhaa ya polynomials yoyote mbili. Njia nyingine inayofanya kazi kwa polynomials zote ni Njia ya Wima. Ni sana kama njia unayotumia kuzidisha idadi nzima. Angalia kwa makini mfano huu wa kuzidisha namba mbili za tarakimu.

    Tatizo la kuzidisha wima linaonyeshwa. Mara 23 46 imeandikwa kwa mstari chini. Chini ya mstari ni 138. Kando 138 imeandikwa “sehemu ya bidhaa.” Chini ya 138 ni 92. Kando 92 imeandikwa “sehemu ya bidhaa.” Chini ya 92 ni mstari na 1058. Kando 1058 imeandikwa “bidhaa.”

    Unaanza kwa kuzidisha 23 na 6 ili kupata 138. Kisha huzidisha 23 na 4, ukitengeneza bidhaa ya sehemu katika nguzo sahihi. Mwisho, unaongeza bidhaa za sehemu. Sasa tutaweza kutumia njia hii hiyo ya kuzidisha binomials mbili.

    Mfano\(\PageIndex{15}\):

    Panua kwa kutumia njia ya wima: (5x - 1) (2x - 7).

    Suluhisho

    Haijalishi ambayo binomial inakwenda juu. Line up nguzo wakati kuzidisha kama tulivyofanya wakati sisi kuzidisha 23 (46).

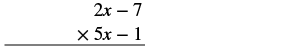      CNX_BMath_Figure_10_03_059_img-01.png
    Panua 2x - 7 na -1. CNX_BMath_Figure_10_03_059_img-02.png
    Kuzidisha 2x - 7 na 5x. CNX_BMath_Figure_10_03_059_img-03.png
    Ongeza kama maneno. 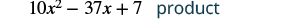CNX_BMath_Figure_10_03_059_img-04.png

    Angalia bidhaa za sehemu ni sawa na maneno katika njia ya FOIL.

    Kwenye kushoto, 5x minus mara 1 2x minus 7 inavyoonyeshwa. Chini ya hiyo ni 10 x squared minus 35x minus 2x pamoja 7. Maneno mawili ya kwanza ni ya bluu, ya pili ya pili katika nyekundu. Chini ya kuwa ni 10 x squared minus 37x plus 7. Kwa upande wa kulia, tatizo la kuzidisha wima linaonyeshwa. 2xx minus mara 7 5x minus 1 imeandikwa kwa mstari chini. Chini ya mstari ni nyekundu hasi 2x pamoja na 7. Chini ya hiyo ni 10 x squared minus 35 x katika bluu. Chini ya hapo, kuna mstari mwingine. Chini ya mstari huo ni 10 x squared minus 37x plus 7.

    Zoezi\(\PageIndex{29}\):

    Panua kwa kutumia njia ya wima: (4m - 9) (3m - 7).

    Jibu

    \( 12 m^{2}-55 m+63\)

    Zoezi\(\PageIndex{30}\):

    Panua kwa kutumia njia ya wima: (6n - 5) (7n - 2).

    Jibu

    \(42 n^{2}-47 n+10 \)

    Sasa tumetumia mbinu tatu za kuzidisha binomials. Hakikisha kufanya mazoezi ya kila njia, na jaribu kuamua ni nani unayopendelea. Mbinu tatu zimeorodheshwa hapa ili kukusaidia kukumbuka.

    Ufafanuzi: Kuzidisha Binomials mbili

    Ili kuzidisha binomials, tumia:

    • Mali ya Kusambaza
    • Njia ya foil
    • Njia ya wima

    Kumbuka, FOIL inafanya kazi tu wakati wa kuzidisha binomials mbili.

    Kuzidisha Trinomial na Binomial

    Tumeongeza monomials na monomials, monomials na polynomials, na binomials na binomials. Sasa tuko tayari kuzidisha trinomial na binomial. Kumbuka, njia ya FOIL haifanyi kazi katika kesi hii, lakini tunaweza kutumia Mali ya Usambazaji au Njia ya Wima. Sisi kwanza kuangalia mfano kwa kutumia Mali Distributive.

    Mfano\(\PageIndex{16}\):

    Panua kwa kutumia Mali ya Mgawanyo: (x + 3) (2x 2 - 5x + 8).

    Suluhisho

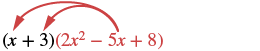      CNX_BMath_Figure_10_03_061_img-01.png
    Kusambaza. CNX_BMath_Figure_10_03_061_img-02.png
    Kuzidisha. 2x 3 - 5x 2 + 8x + 6x 2 - 15x + 24
    Kuchanganya kama maneno. 2x 3 + x 2 - 7x + 24
    Zoezi\(\PageIndex{31}\):

    Panua kwa kutumia Mali ya Mgawanyo: (y - 1) (y 2 - 7y + 2).

    Jibu

    \( y^{3}-8 y^{2}+9 y-2\)

    Zoezi\(\PageIndex{32}\):

    Panua kwa kutumia Mali ya Mgawanyo: (x + 2) (3x 2 - 4x + 5).

    Jibu

    \( 3 x^{3}+2 x^{2}-3 x+10\)

    Sasa hebu tufanye kuzidisha sawa kwa kutumia Njia ya Wima.

    Mfano\(\PageIndex{17}\):

    Panua kwa kutumia Njia ya Wima: (x + 3) (2x 2 - 5x + 8).

    Suluhisho

    Ni rahisi kuweka polynomial na maneno machache chini kwa sababu tunapata bidhaa chache za sehemu kwa njia hii.

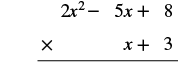      CNX_BMath_Figure_10_03_062_img-01.png
    Kuzidisha (2x 2 - 5x + 8) na 3. 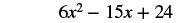CNX_BMath_Figure_10_03_062_img-02.png
    Kuzidisha (2x 2 - 5x + 8) na x. 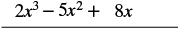CNX_BMath_Figure_10_03_062_img-03.png
    Ongeza kama maneno. 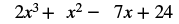CNX_BMath_Figure_10_03_062_img-04.png
    Zoezi\(\PageIndex{33}\):

    Panua kwa kutumia Njia ya Wima: (y - 1) (y 2 - 7y + 2).

    Jibu

    \(y^{3}-8 y^{2}+9 y-2 \)

    Zoezi\(\PageIndex{34}\):

    Panua kwa kutumia Njia ya Wima: (x + 2) (3x 2 - 4x + 5).

    Jibu

    \( 3 x^{3}+2 x^{2}-3 x+10\)

    PATA RASILIMALI ZA ZIADA

    Kuzidisha Monomials

    Kuzidisha Polynomials

    Kuzidisha Polynomials 2

    Kuzidisha Polynomials Tathmini

    Kuzidisha Polynomials Kutumia Mali ya Kusambaza

    Kuzidisha Binomials

    Mazoezi hufanya kamili

    Kuzidisha Polynomial na Monomial

    Katika mazoezi yafuatayo, ongeze.

    1. 4 (x + 10)
    2. (6 y + 8)
    3. 15 (r - 24)
    4. 12 (v - 30)
    5. -3 (m + 11)
    6. -4 (p + 15)
    7. -8 (z - 5)
    8. -3 (x - 9)
    9. (u + 5)
    10. q (q + 7)
    11. (n 2 - 3n)
    12. (s 2 - 6s)
    13. 12x (x - 10)
    14. 9m (m - 11)
    15. -9a (3a + 5)
    16. -4p (2p + 7)
    17. 6x (4x + y)
    18. 5a (9a + b)
    19. 5p (11p - 5q)
    20. 12u (3u - 4v)
    21. 3 (v 2 + 10v + 25)
    22. 6 (x 2 + 8x + 16)
    23. 2n (4n 2 - 4n + 1)
    24. 3r (2r 2 - 6r + 2)
    25. -8y (y 2 + 2y - 15)
    26. -5m (m 2 + 3m - 18)
    27. 5q 3 (q 2 - 2q + 6)
    28. 9r (3 r 2 - 3r + 5)
    29. -4z 2 (3z 2 + 12z - 1)
    30. -3x 2 (7x 2 + 10x - 1)
    31. (2y - 9)
    32. (8b - 1 b)
    33. (w - 6) • 8
    34. (k - 4) • 5

    Kuzidisha Binomial na Binomial

    Katika mazoezi yafuatayo, kuzidisha binomials zifuatazo kwa kutumia: (a) Mali ya Kusambaza (b) njia ya FOIL (c) njia ya wima

    1. (x + 4) (x + 6)
    2. (u + 8) (u + 2)
    3. (n + 12) (n - 3)
    4. (y + 3) (y - 9)

    Katika mazoezi yafuatayo, kuzidisha binomials zifuatazo. Tumia njia yoyote.

    1. (y + 8) (y + 3)
    2. (x + 5) (x + 9)
    3. (a + 6) (a + 16)
    4. (q + 8) (q + 12)
    5. (u - 5) (u - 9)
    6. (r - 6) (r - 2)
    7. (z - 10) (z - 22)
    8. (b - 5) (b - 24)
    9. (x - 4) (x + 7)
    10. (s - 3) (s + 8)
    11. (v + 12) (v - 5)
    12. (d + 15) (d - 4)
    13. (6n + 5) (n + 1)
    14. (7y + 1) (y + 3)
    15. (2m - 9) (10m + 1)
    16. (5r - 4) (12r + 1)
    17. (4c - 1) (4c + 1)
    18. (8n - 1) (8n + 1)
    19. (3u - 8) (5u - 14)
    20. (2q - 5) (7q - 11)
    21. (a + b) (2a + 3b)
    22. (r + s) (3r + 2s)
    23. (5x - y) (x - 4)
    24. (4z - y) (z - 6)

    Kuzidisha Trinomial na Binomial

    Katika mazoezi yafuatayo, kuzidisha kutumia (a) Mali ya Usambazaji na (b) Njia ya Wima.

    1. (u + 4) (u 2 + 3u + 2)
    2. (x + 5) (x 2 + 8x + 3)
    3. (a + 10) (3a 2 + a - 5)
    4. (n + 8) (4n 2 + n - 7)

    Katika mazoezi yafuatayo, ongeze. Tumia njia yoyote.

    1. (y - 6) (y 2 - 10y + 9)
    2. (k - 3) (k 2 - 8k + 7)
    3. (2x + 1) (x 2 - 5x - 6)
    4. (5v + 1) (v 2 - 6v - 10)

    kila siku Math

    1. Hesabu ya akili Unaweza kutumia kuzidisha binomial kuzidisha idadi bila calculator. Sema unahitaji kuzidisha mara 13 15. Fikiria 13 kama 10 + 3 na 15 kama 10 + 5.
      1. Panua (10 + 3) (10 + 5) kwa njia ya FOIL.
      2. Panua 13 • 15 bila kutumia calculator.
      3. Njia ipi ni rahisi kwako? Kwa nini?
    2. Hesabu ya akili Unaweza kutumia kuzidisha binomial kuzidisha idadi bila calculator. Sema unahitaji kuzidisha mara 18 17. Fikiria 18 kama 20 ÷ 2 na 17 kama 20 - 3.
      1. Panua (20 ÷ 2) (20 ÷ 3) kwa njia ya FOIL.
      2. Panua 18 • 17 bila kutumia calculator.
      3. Njia ipi ni rahisi kwako? Kwa nini?

    Mazoezi ya kuandika

    1. Ni njia gani unapendelea kutumia wakati wa kuzidisha binomial mbili-Mali ya Usambazaji, njia ya FOIL, au Njia ya Wima? Kwa nini?
    2. Ni njia gani unapendelea kutumia wakati wa kuzidisha trinomial kwa binomial - Mali ya Usambazaji au Njia ya Wima? Kwa nini?

    Self Check

    (a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

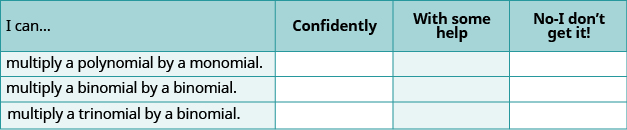
    CNX_BMath_Figure_AppB_061.jpg

    (b) Orodha hii inakuambia nini kuhusu ustadi wako wa sehemu hii? Ni hatua gani utachukua ili kuboresha?

    Wachangiaji na Majina