Skip to main content
Global

10.2: Tumia Mali ya kuzidisha ya Watazamaji (Sehemu ya 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    173434

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Kurahisisha maneno na watazamaji
    • Kurahisisha maneno kwa kutumia Bidhaa Mali ya Watazamaji
    • Kurahisisha maneno kwa kutumia Mali ya Nguvu ya Watazamaji
    • Kurahisisha maneno kwa kutumia Bidhaa kwa Mali ya Nguvu
    • Kurahisisha maneno kwa kutumia mali kadhaa
    • Kuzidisha monomials
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kurahisisha:\(\dfrac{3}{4} \cdot \dfrac{3}{4}\). Ikiwa umekosa tatizo, kagua Mfano 4.3.7.
    2. Kurahisisha: (-2) (-2) (-2). Ikiwa umekosa tatizo, tathmini Mfano 3.7.6.

    Kurahisisha Maneno na Watazamaji

    Kumbuka kwamba exponent inaonyesha kuzidisha mara kwa mara ya kiasi sawa. Kwa mfano, 2 4 ina maana ya kuzidisha mambo manne ya 2, hivyo 2 4 ina maana 2 • 2 • 2 • 2. Fomu hii inajulikana kama nukuu ya kielelezo.

    Ufafanuzi: Nukuu ya kielelezo

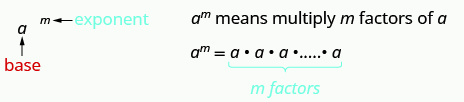
    Kwenye upande wa kushoto, kukulia kwa m inavyoonyeshwa. m ni lebo katika bluu kama exponent. a ni kinachoitwa katika nyekundu kama msingi. Kwa upande wa kulia, inasema kwa m ina maana kuzidisha m sababu za a Chini ya hii, inasema a kwa m sawa mara mara a, na m sababu zilizoandikwa hapa chini katika bluu.

    Hii ni kusoma kwa m th nguvu.

    Katika kujieleza m, exponent inatuambia mara ngapi sisi kutumia msingi a kama sababu.

    Kwenye upande wa kushoto, 7 hadi nguvu ya 3 inavyoonyeshwa. Chini ni mara 7 mara 7, na mambo 3 yaliyoandikwa hapa chini. Kwenye upande wa kulia, mabano hasi 8 hadi nguvu ya 5 huonyeshwa. Chini ni hasi mara 8 hasi mara 8 hasi mara 8 hasi mara 8 hasi 8, na mambo 5 yaliyoandikwa hapa chini.

    Kabla ya kuanza kufanya kazi na maneno variable zenye exponents, hebu kurahisisha maneno machache kuwashirikisha idadi tu.

    Mfano\(\PageIndex{1}\):

    Kurahisisha: (a) 5 3 (b) 9 1

    Suluhisho

    (a) 5 3

    Kuzidisha mambo 3 ya 5. 5 • 5 • 5
    Kurahisisha. 125

    (b) 9 1

    Kuzidisha 1 sababu ya 9. 9
    Zoezi\(\PageIndex{1}\):

    Kurahisisha: (a) 4 3 (b) 11 1

    Jibu

    64

    Jibu b

    11

    Zoezi\(\PageIndex{2}\):

    Kurahisisha: (a) 3 4 (b) 21 1

    Jibu

    81

    Jibu b

    21

    Mfano\(\PageIndex{2}\):

    Kurahisisha:\(\left(\dfrac{7}{8}\right)^{2}\) (a) (b) (0.74) 2

    Suluhisho

    (a)\(\left(\dfrac{7}{8}\right)^{2}\)

    Panua mambo mawili. $$\ kushoto (\ dfrac {7} {8}\ kulia)\ kushoto (\ dfrac {7} {8}\ haki) $$
    Kurahisisha. $$\ dfrac {49} {64} $$

    (b) (0.74) 2

    Panua mambo mawili. (0.74) (0.74)
    Kurahisisha. 0.5476
    Zoezi\(\PageIndex{3}\):

    Kurahisisha:\(\left(\dfrac{5}{8}\right)^{2}\) (a) (b) (0.67) 2

    Jibu

    \(\frac{25}{64}\)

    Jibu b

    0.4489

    Zoezi\(\PageIndex{4}\):

    Kurahisisha:\(\left(\dfrac{2}{5}\right)^{3}\) (a) (b) (0.127) 2

    Jibu

    \(\frac{8}{125}\)

    Jibu b

    0.016129

    Mfano\(\PageIndex{3}\):

    Kurahisisha: (a) (—3) 4 (b) —3 4

    Suluhisho

    (a) (—3) 4

    Kuzidisha mambo manne ya 1-3. (1-3) (-3) (1-3) (1-3)
    Kurahisisha. 81

    (b) —3 4

    Panua mambo mawili. - (3 • 3 • 3 • 3)
    Kurahisisha. -81

    Angalia kufanana na tofauti katika sehemu (a) na (b). Kwa nini majibu ni tofauti? Katika sehemu (a) mabano yanatuambia kuinua (1-3) hadi nguvu ya 4. Katika sehemu (b) sisi kuongeza tu 3 hadi 4 th nguvu na kisha kupata kinyume.

    Zoezi\(\PageIndex{5}\):

    Kurahisisha: (a) (-2) 4 (b) -1 4

    Jibu

    16

    Jibu b

    -16

    Zoezi\(\PageIndex{6}\):

    Kurahisisha: (a) (-8) 2 (b) -8 2

    Jibu

    64

    Jibu b

    -64

    Kurahisisha Maneno Kutumia Mali ya Bidhaa ya Watazamaji

    Umeona kwamba unapochanganya maneno kama hayo kwa kuongeza na kutoa, unahitaji kuwa na msingi sawa na kielelezo sawa. Lakini wakati wewe kuzidisha na kugawanya, exponents inaweza kuwa tofauti, na wakati mwingine besi inaweza kuwa tofauti, pia. Tutaweza hupata mali ya exponents kwa kuangalia kwa mwelekeo katika mifano kadhaa. Mali yote exponent kushikilia kweli kwa idadi yoyote halisi, lakini hivi sasa sisi tu kutumia idadi nzima exponents.

    Kwanza, tutaangalia mfano unaoongoza kwenye Mali ya Bidhaa.

      $x^ {2}\ dot x ^ {2} $$
    Hii ina maana gani? Ni mambo ngapi kabisa? 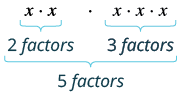CNX_BMath_Figure_10_02_015_img-02.png
    Hivyo, tuna $x^ {5} $$
    Kumbuka kwamba 5 ni jumla ya exponents, 2 na 3. $x^ {2}\ cdot x^ {3}\; ni\; x^ {2+3},\; au\; x^ {5} $$
    Tunaandika: $$\ kuanza {kupasuliwa} &x^ {2}\ cdot x^ {3}\\ &x^ {2+3}\\ &x^ {5}\ mwisho {mgawanyiko} $$

    Msingi ulikaa sawa na sisi aliongeza exponents. Hii inasababisha Bidhaa Mali kwa Exponents.

    Ufafanuzi: Bidhaa Mali ya Watazamaji

    Ikiwa ni namba halisi na m, n ni kuhesabu namba, basi

    \[a^{m} \cdot a^{n} = a^{m + n}\]

    Ili kuzidisha na besi kama, ongeza vielelezo.

    Mfano na namba husaidia kuthibitisha mali hii.

    \[\begin{split} 2^{2} \cdot 2^{3} &\stackrel{?}{=} 2^{2+3} \\ 4 \cdot 8 &\stackrel{?}{=} 2^{5} \\ 32 &= 32\; \checkmark \end{split}\]

    Mfano\(\PageIndex{4}\):

    kurahisisha: x 5 • x 7.

    Suluhisho

    Tumia mali ya bidhaa, m • n = m + n. $x^ {\ textcolor {nyekundu} {5+7}} $$
    Kurahisisha. $x^ {12} $$
    Zoezi\(\PageIndex{7}\):

    kurahisisha: x 7 • x 8.

    Jibu

    x 15

    Zoezi\(\PageIndex{8}\):

    kurahisisha: x 5 • x 11.

    Jibu

    x 16

    Mfano\(\PageIndex{5}\):

    kurahisisha: b 4 • b.

    Suluhisho

    Andika upya, b = b 1. $b^ {4}\ cdot b^ {1} $$
    Tumia mali ya bidhaa, m • n = m + n. $$b^ {\ textcolor {nyekundu} {4+1}} $$
    Kurahisisha. $$ b^ {5} $$
    Zoezi\(\PageIndex{9}\):

    Kurahisisha: p 9 • p.

    Jibu

    p 10

    Zoezi\(\PageIndex{10}\):

    Kurahisisha: m • m 7.

    Jibu

    m 8

    Mfano\(\PageIndex{6}\):

    kurahisisha: 2 7 • 2 9.

    Suluhisho

    Tumia mali ya bidhaa, m • n = m + n. $2^ {\ rangi ya maandishi {nyekundu} {7+9}} $$
    Kurahisisha. $2^ {16} $$
    Zoezi\(\PageIndex{11}\):

    kurahisisha: 6 • 6 9.

    Jibu

    6 10

    Zoezi\(\PageIndex{12}\):

    kurahisisha: 9 6 • 9 9.

    Jibu

    9 15

    Mfano\(\PageIndex{7}\):

    kurahisisha: y 17 • y 23.

    Suluhisho

    Taarifa, besi ni sawa, hivyo kuongeza exponents. $$y^ {\ textcolor {nyekundu} {17+23}} $$
    Kurahisisha. $y^ {40} $$
    Zoezi\(\PageIndex{13}\):

    kurahisisha: na 24 • y 19.

    Jibu

    na 43

    Zoezi\(\PageIndex{14}\):

    kurahisisha: z 15 • z 24.

    Jibu

    z 39

    Tunaweza kupanua Bidhaa Mali ya Exponents kwa sababu zaidi ya mbili.

    Mfano\(\PageIndex{8}\):

    kurahisisha: x 3 • x 4 • x 2.

    Suluhisho

    Ongeza vielelezo, kwani besi ni sawa. $x^ {\ textcolor {nyekundu} {3+4+2}} $$
    Kurahisisha. $x^ {9} $$
    Zoezi\(\PageIndex{15}\):

    kurahisisha: x 7 • x 5 • x 9.

    Jibu

    x 21

    Zoezi\(\PageIndex{16}\):

    kurahisisha: y 3 • y 8 • y 4.

    Jibu

    na 15

    Kurahisisha Maneno Kutumia Mali ya Nguvu ya Wasanii

    Sasa hebu tuangalie usemi wa kielelezo ambao una nguvu iliyoinuliwa kwa nguvu. Angalia kama unaweza kugundua mali ya jumla.

      $$ (x^ {2}) ^ {3} $$
    Hii ina maana gani? $x^ {2}\ dot x ^ {2}\ dot x ^ {2} $
    Ni mambo ngapi kabisa? 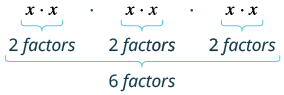CNX_BMath_Figure_10_02_021_img-03.png
    Hivyo, tuna $x^ {6} $$
    Kumbuka kwamba 6 ni bidhaa ya exponents, 2 na 3. $$ (x^ {2}) ^ {3}\; ni\; x^ {2\ cdot 3}\; au\; x^ {6} $$
    Tunaandika: $$\ kuanza {kupasuliwa} & (x^ {2}) ^ {3}\\ &x^ {2\ cdot 3}\\ &x^ {6}\ mwisho {mgawanyiko} $$

    Sisi kuzidisha exponents. Hii inasababisha Power Mali kwa Exponents.

    Ufafanuzi: Nguvu Mali ya Watazamaji

    Ikiwa ni namba halisi na m, n ni namba nzima, basi

    \[(a^{m})^{n} = a^{m \cdot n}\]

    Ili kuongeza nguvu kwa nguvu, kuzidisha wafuasi.

    Mfano na namba husaidia kuthibitisha mali hii.

    \[\begin{split} (5^{2})^{3} &\stackrel{?}{=} 5^{2 \cdot 3} \\ (25)^{3} &\stackrel{?}{=} 5^{6} \\ 15,625 &= 15,625\; \checkmark \end{split}\]

    Mfano\(\PageIndex{9}\):

    Kurahisisha: (a) (x 5) 7 (b) (3 6) 8

    Suluhisho

    (a) (x 5) 7

    Tumia Mali ya Nguvu, (m) n = m • n. $x^ {\ textcolor {nyekundu} {5\ cdot 7}} $$
    Kurahisisha. $x^ {35} $$

    (b) (3 6) 8

    Tumia Mali ya Nguvu, (m) n = m • n. $3^ {\ textcolor {nyekundu} {6\ cdot 8}} $
    Kurahisisha. $x^ {48} $$
    Zoezi\(\PageIndex{17}\):

    Kurahisisha: (a) (x 7) 4 (b) (7 4) 8

    Jibu

    x 28

    Jibu b

    7 32

    Zoezi\(\PageIndex{18}\):

    Kurahisisha: (a) (x 6) 9 (b) (8 6) 7

    Jibu

    na 54

    Jibu b

    8 42

    Wachangiaji na Majina