10.1: Kuongeza na Ondoa Polynomials

Malengo ya kujifunza

• Kutambua polynomials, monomials, binomials, na trinomials
• Kuamua kiwango cha polynomials
• Ongeza na uondoe monomials
• Ongeza na uondoe polynomials
• Tathmini polynomial kwa thamani iliyotolewa

kuwa tayari!

Kabla ya kuanza, fanya jaribio hili la utayari.

1. kurahisisha: 8x + 3x. Ikiwa umekosa tatizo hili, kagua Mfano 2.3.10.
2. Ondoa: (5n + 8) - (2n - 1). Kama amekosa tatizo hili, mapitio Mfano 7.4.13.
3. Tathmini: 4y ² wakati y = 5 Kama amekosa tatizo hili, mapitio Mfano 2.3.6.

Kutambua Polynomials, Monomials, Binomials, na Trinomials

Katika Kutathmini, Kurahisisha, na Tafsiri Maneno, umejifunza kwamba neno ni mara kwa mara au bidhaa ya vigezo vya mara kwa mara na moja au zaidi. Wakati ni ya shaba ya fomu ^m, ambapo a ni mara kwa mara na m ni namba nzima, inaitwa monomial. Monomial, au jumla na/au tofauti ya monomials, inaitwa polynomial.

Ufafanuzi: Polynomials

polynomial — monomial, au monomials mbili au zaidi, pamoja na kuongeza au kutoa

monomial — polynomial na hasa neno moja

binomial — polynomial na maneno mawili

trinomial — polynomial na maneno hasa tatu

Angalia mizizi:

• aina nyingi - ina maana wengi
• mono - inamaanisha moja
• bi - ina maana mbili
• tri - ina maana tatu

Hapa ni baadhi ya mifano ya polynomials:

Polynomial	b + 1	4y ^2 - 7y + 2	5x ^5 - 4x ^4 + x ^3 + 8x ^2 - 9x + 1
Monomial	5	4b ^2	-9x ^3
Binomial	3a - 7	na ^2 - 9	17x ^3 + 14x ^2
Trinomial	x ^2 - 5x + 6	4y ^2 - 7y + 2	5a ^4 - 3a ^3 + a

Angalia kwamba kila monomial, binomial, na trinomial pia ni polynomial. Wao ni wanachama maalum wa familia ya polynomials na hivyo wana majina maalum. Tunatumia maneno 'monomial', 'binomial', na 'trinomial' wakati wa kutaja polynomials hizi maalum na tu kuwaita wengine wote 'polynomials'.

Mfano\(\PageIndex{1}\):

Kuamua kama kila polynomial ni monomial, binomial, trinomial, au polynomial nyingine: (a) 8x ² - 7x - 9 (b) -5a ⁴ (c) x ⁴ - 7x ³ - 6x ² + 5x 2 (d) 11 - 4y ³ (e) n

Suluhisho

Polynomial	Idadi ya maneno	Aina
(a) 8x ^2 - 7x - 9	3	Trinomial
(b) -5a ^4	1	Monomial
(c) x ^4 - 7x ^3 - 6x ^2 + 5x + 2	5	Polynomial
(d) 11 - 4y ^3	2	Binomial
(e)	1	Monomial

Zoezi\(\PageIndex{1}\):

Kuamua kama kila polynomial ni monomial, binomial, trinomial, au polynomial nyingine. (a) z (b) 2x ³ - 4x ² - x - 8 (c) 6x ² - 4x + 1 (d) 9 - 4y ² (e) 3x ⁷

Jibu

monomial

Jibu b

polynomial

Jibu c

ya trinomial

Jibu d

binomial

Jibu e

monomial

Zoezi\(\PageIndex{2}\):

Kuamua kama kila polynomial ni monomial, binomial, trinomial, au polynomial nyingine. (a) y ³ - 8 (b) 9x ³ - 5x ² - x (c) x ⁴ - 3x ² - 4x - 7 (d) -y ⁴ (e) w

Jibu

binomial

Jibu b

ya trinomial

Jibu c

polynomial

Jibu d

monomial

Jibu e

monomial

Kuamua Shahada ya Polynomials

Katika sehemu hii, tutafanya kazi na polynomials ambazo zina variable moja tu katika kila muda. Kiwango cha polynomial na kiwango cha masharti yake ni kuamua na exponents ya variable.

Monomial ambayo haina kutofautiana, tu mara kwa mara, ni kesi maalum. Kiwango cha mara kwa mara ni 0 - haina kutofautiana.

Ufafanuzi: Shahada ya Polynomial

Kiwango cha neno ni kielelezo cha kutofautiana kwake.

Kiwango cha mara kwa mara ni 0.

Kiwango cha polynomial ni kiwango cha juu cha masharti yake yote.

Hebu tuone jinsi hii inavyofanya kazi kwa kuangalia polynomials kadhaa. Tutachukua hatua kwa hatua, kuanzia na monomials, na kisha kuendelea kwa polynomials na maneno zaidi.

Kumbuka: Msingi wowote imeandikwa bila exponent ina exponent alisema ya 1.

Mfano\(\PageIndex{2}\):

Pata shahada ya polynomials zifuatazo: (a) 4x (b) 3x ³ - 5x + 7 (c) -11 (d) -6x ² + 9x -3 (e) 8x + 2

Suluhisho

(a) 4x

Mtazamo wa x ni moja. x = x ^1

Shahada ni 1.

(b) 3x ³ - 5x + 7

Kiwango cha juu cha masharti yote ni 3.

Shahada ni 3.

(c) -11

Kiwango cha mara kwa mara ni 0.

Shahada ni 0.

(d) -6x ² + 9x - 3

Kiwango cha juu cha masharti yote ni 2.

Shahada ni 2.

(e) 8x + 2

Kiwango cha juu cha masharti yote ni 1.

Shahada ni 1.

Zoezi\(\PageIndex{3}\):

Pata shahada ya polynomials zifuatazo: (a) -6y (b) 4x - 1 (c) 3x ⁴ + 4x ² - 8 (d) 2y ² + 3y 9 (e) -18

Jibu

1

Jibu b

1

Jibu c

4

Jibu d

2

Jibu e

0

Zoezi\(\PageIndex{4}\):

Pata kiwango cha polynomials zifuatazo: (a) 47 (b) 2x ² - 8x + 2 (c) x ⁴ - 16 (d) y ⁵ - 5y ³ + y (e) 9a ³

Jibu

0

Jibu b

2

Jibu c

4

Jibu d

5

Jibu e

3

Kufanya kazi na polynomials ni rahisi wakati unapoorodhesha maneno katika utaratibu wa kushuka kwa digrii. Wakati polynomial imeandikwa kwa njia hii, inasemekana kuwa katika fomu ya kawaida. Angalia nyuma katika polynomials katika Mfano 10.2. Angalia kwamba wote wameandikwa kwa fomu ya kawaida. Pata tabia ya kuandika neno kwa shahada ya juu kwanza.

Kuongeza na Ondoa Monomials

Katika Lugha ya Algebra, ulirahisisha maneno kwa kuchanganya maneno kama hayo. Kuongeza na kuondoa monomials ni sawa na kuchanganya maneno kama hayo. Kama maneno lazima iwe na variable sawa na exponent sawa. Kumbuka kwamba wakati wa kuchanganya kama maneno tu coefficients ni pamoja, kamwe exponents.

Mfano\(\PageIndex{3}\):

Kuongeza: 17x ² + 6x ².

Suluhisho

Kuchanganya kama maneno.

23x ^2

Zoezi\(\PageIndex{5}\):

Kuongeza: 12x ² + 5x ².

Jibu

17x ²

Zoezi\(\PageIndex{6}\):

Ongeza: -11y ² + 8y ².

Jibu

-3y ²

Mfano\(\PageIndex{4}\):

Ondoa: 11n - (-8n).

Suluhisho

Kuchanganya kama maneno.

19n

Zoezi\(\PageIndex{7}\):

Ondoa: 9n - (-5n).

Jibu

14n

Zoezi\(\PageIndex{8}\):

Ondoa: -7a ³ - (-5a ³).

Jibu

-2a ³

Mfano\(\PageIndex{5}\):

kurahisisha: a ² + 4b ² - 7a ².

Suluhisho

Kuchanganya kama maneno.

-6a ^2 + 4b ^2

Kumbuka, -6a ² na 4b ² si kama maneno. Vigezo si sawa.

Zoezi\(\PageIndex{9}\):

Kuongeza: 3x ² + 3y ² - 5x ².

Jibu

-2x ² + 3y ²

Zoezi\(\PageIndex{10}\):

Kuongeza: 2a ² + b ² - 4a ².

Jibu

-2a ² + b ²

Kuongeza na Ondoa Polynomials

Kuongeza na kuondoa polynomials inaweza kufikiriwa kama kuongeza tu na kuondoa kama maneno. Angalia kwa masharti kama - wale walio na vigezo sawa na exponent sawa. Mali ya Commutative inatuwezesha kupanga upya masharti ili kuweka maneno kama pamoja. Inaweza pia kuwa na manufaa kusisitiza, mduara, au sanduku kama maneno.

Mfano\(\PageIndex{6}\):

Pata jumla: (4x ² - 5x + 1) + (3x ² - 8x - 9)

Suluhisho

Tambua maneno kama hayo.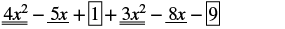
Panga upya ili kupata maneno kama hayo pamoja.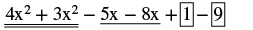
Kuchanganya kama maneno.

Zoezi\(\PageIndex{11}\):

Pata jumla: (3x ² - 2x + 8) + (x ² - 6x + 2).

Jibu

4x ² - 8x + 10

Zoezi\(\PageIndex{12}\):

Pata jumla: (7y ² + 4y - 6) + (4y ² + 5y + 1)

Jibu

11y ² + 9y - 5

Mabano ni alama za makundi. Wakati sisi kuongeza polynomials kama tulivyofanya katika Mfano 10.6, tunaweza kuandika upya kujieleza bila mabano na kisha kuchanganya kama maneno. Lakini tunapoondoa polynomials, lazima tuwe makini sana na ishara.

Mfano\(\PageIndex{7}\):

Pata tofauti: (7u ² - 5u + 3) - (4u ² - 2).

Suluhisho

Kusambaza na kutambua maneno kama hayo.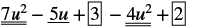
Panga upya masharti.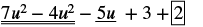
Kuchanganya kama maneno.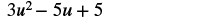

Zoezi\(\PageIndex{13}\):

Pata tofauti: (6y ² + 3y - 1) - (3y ² - 4).

Jibu

3y ² + 3y + 3

Zoezi\(\PageIndex{14}\):

Pata tofauti: (8u ² - 7u - 2) - (5u ² - 6u - 4).

Jibu

3u ² - u + 2

Mfano\(\PageIndex{8}\):

Ondoa: (m ² - 3m + 8) kutoka (9m ² - 7m + 4).

Suluhisho

Kusambaza na kutambua maneno kama hayo.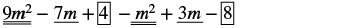
Panga upya masharti.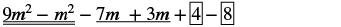
Kuchanganya kama maneno.

Zoezi\(\PageIndex{15}\):

Ondoa: (4n ² - 7n - 3) kutoka (8n ² + 5n - 3).

Jibu

4n ² + 12

Zoezi\(\PageIndex{16}\):

Ondoa: (a ² - 4a - 9) kutoka (6a ² + 4a - 1).

Jibu

5a ² + 8a + 8

Tathmini Polynomial kwa Thamani iliyotolewa

Katika Lugha ya Algebra tulipima maneno. Tangu polynomials ni maneno, tutaweza kufuata taratibu hiyo ya kutathmini polynomials-mbadala thamani iliyotolewa kwa ajili ya kutofautiana katika polynomial, na kisha kurahisisha.

Mfano\(\PageIndex{9}\):

Tathmini 3x 2 - 9x + 7 wakati (a) x = 3 (b) x = -1

Suluhisho

(a) x = 3

mbadala 3 kwa x.	3 (3) ^2 - 9 (3) + 7
Kurahisisha kujieleza na exponent.	3 • 9 - 9 (3) + 7
Kuzidisha.	27-27 + 7
Kurahisisha.	7

(b) x = -1

Mbadala -1 kwa x.	3 (-1) ^2 - 9 (-1) + 7
Kurahisisha kujieleza na exponent.	3 • 1 - 9 (-1) + 7
Kuzidisha.	3 + 9 + 7
Kurahisisha.	19

Zoezi\(\PageIndex{17}\):

Tathmini: 2x ² + 4x - 3 wakati (a) x = 2 (b) x = -3

Jibu

13

Jibu b

3

Zoezi\(\PageIndex{18}\):

Tathmini: 7y ² - y - 2 wakati (a) y = -4 (b) y = 0

Jibu

114

Jibu b

-2

Mfano\(\PageIndex{10}\):

Polynomial -16t 2 + 300 inatoa urefu wa kitu t sekunde baada ya kushuka kutoka daraja la urefu wa mguu 300. Pata urefu baada ya t = sekunde 3.

Suluhisho

Mbadala 3 kwa ajili yake.	-16 (3) ^2 + 300
Kurahisisha kujieleza na exponent.	-16 • 9 + 300
Kuzidisha.	-144 + 300
Kurahisisha.	156

Zoezi\(\PageIndex{19}\):

Polynomial -8t ² + 24t + 4 inatoa urefu, kwa miguu, wa mpira t sekunde baada ya kupigwa hewa, kutoka urefu wa awali wa futi 4. Pata urefu baada ya t = sekunde 3.

Jibu

4 miguu

Zoezi\(\PageIndex{20}\):

Polynomial -8t ² + 24t + 4 inatoa urefu, kwa miguu, ya mpira x sekunde baada ya kupigwa hewa, kutoka urefu wa awali wa miguu 4. Pata urefu baada ya sekunde t = 2.

Jibu

Miguu 20

PATA RASILIMALI ZA ZIADA

Kuongeza Polynomials

Kutoa Polynomials

Mazoezi hufanya kamili

Kutambua Polynomials, Monomials, Binomials na Trinomials

Katika mazoezi yafuatayo, onyesha kama kila moja ya polynomials ni monomial, binomial, trinomial, au polynomial nyingine.

1. 5x 2
2. z ² - 5z - 6
3. a ² + 9a + 18
4. -12p ⁴
5. y ³ - 8y ² + 2y - 16
6. 10 - 9x
7. 23y ²
8. m ⁴ + 4m ³ + 6m ² + 4m + 1

Kuamua Shahada ya Polynomials

Katika mazoezi yafuatayo, tambua kiwango cha kila polynomial.

9. 8a ⁵ - 2a ³ + 1
10. 5c ³ + 11c ² - c - 8
11. 3x - 12
12. 4y + 17
13. —13
14. -22

Kuongeza na Ondoa Monomials

Katika mazoezi yafuatayo, ongeza au uondoe monomials.

15. 6x ² + 9x ²
16. 4y ³ + 6y ³
17. -12u + 4u
18. -3m + 9m
19. 5a + 7b
20. 8g + 6z
21. Ongeza: 4a, - 3b, - 8a
22. Ongeza: 4x, 3y, - 3x
23. 18x - 2x
24. 13a-3a
25. Ondoa 5x ⁶ kutoka - 12x ⁶
26. Ondoa 2p ⁴ kutoka - 7p ⁴

Kuongeza na Ondoa Polynomials

Katika mazoezi yafuatayo, ongeza au uondoe polynomials.

27. (4y ² + 10y + 3) + (8y ² - 6y + 5)
28. (7x ² - 9x + 2) + (6x ² - 4x + 3)
29. (x ² + 6x + 8) + (-4x ² + 11x - 9)
30. (y ² + 9y + 4) + (-2y ² - 5y - 1)
31. (3a ² + 7) + (a ² - 7a - 18)
32. (p ² - 5p - 11) + (3p ² + 9)
33. (6m ² - 9m - 3) - (2m ² + m - 5)
34. (3n ² - 4n + 1) - (4n ² - n - 2)
35. (z ² + 8z + 9) - (z ² - 3z + 1)
36. (z ² - 7z + 5) - (z ² - 8z + 6)
37. (12s ² - 15s) - (s - 9)
38. (10r ² - 20r) - (r - 8)
39. Pata jumla ya (2p ³ - 8) na (p ² + 9p + 18)
40. Pata jumla ya (q ² + 4q + 13) na (7q ³ - 3)
41. Ondoa (7x ² - 4x + 2) kutoka (8x ² - x + 6)
42. Ondoa (5x ² - x + 12) kutoka (9x ² - 6x - 20)
43. Pata tofauti ya (w ² + w - 42) na (w ² - 10w + 24)
44. Pata tofauti ya (z ² - 3z - 18) na (z ² + 5z - 20)

Tathmini Polynomial kwa Thamani iliyotolewa

Katika mazoezi yafuatayo, tathmini kila polynomial kwa thamani iliyotolewa.

45. Tathmini 8y ² - 3y + 2
    1. y = 5
    2. y = -2
    3. y = 0
46. Tathmini 5y ² - y - 7 wakati:
    1. y = -4
    2. y = 1
    3. y = 0
47. Tathmini 4 - 36x wakati:
    1. x = 3
    2. x = 0
    3. x = -1
48. Tathmini 16 - 36x ² wakati:
    1. x = -1
    2. x = 0
    3. x = 2
49. Washer dirisha matone squeegee kutoka jukwaa 275 miguu juu. Polynomial -16t ² + 275 inatoa urefu wa squeegee t sekunde baada ya kushuka. Pata urefu baada ya t = sekunde 4.
50. Mtengenezaji wa sehemu zote za microwave amegundua kwamba mapato yaliyopatikana kutokana na kuuza microwaves kwa gharama ya dola p kila mmoja hutolewa na polynomial -5p ² + 350p. Pata mapato yaliyopokelewa wakati p = dola za 50.

kila siku Math

51. Ufanisi wa mafuta Ufanisi wa mafuta (kwa maili kwa kila lita) ya basi inayoenda kwa kasi ya maili x kwa saa hutolewa na polynomial\(− \dfrac{1}{160} x^{2} + \dfrac{1}{2} x\). Kupata ufanisi wa mafuta wakati x = 40 mph.
52. Kuacha Umbali Idadi ya miguu inachukua kwa gari linalosafiri kwa maili x kwa saa ili kuacha kavu, kiwango cha saruji hutolewa na 0.06x ² + 1.1x ya polynomial. Pata umbali wa kuacha wakati x = 60 mph.

Mazoezi ya kuandika

53. Kutumia maneno yako mwenyewe, kuelezea tofauti kati ya monomial, binomial, na trinomial.
54. Eloise anadhani jumla 5x ² + 3x ⁴ ni 8x ⁶. Ni nini kibaya na hoja yake?

Self Check

(a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

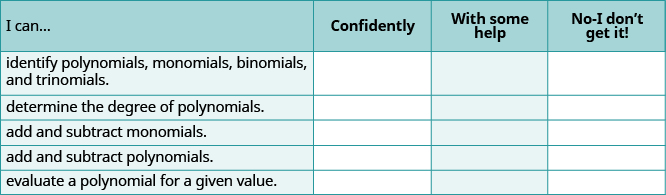
(b) Kama wengi wa hundi yako walikuwa:

... kwa ujasiri. Hongera! Umefanikiwa malengo katika sehemu hii. Fikiria ujuzi wa kujifunza uliyotumia ili uweze kuendelea kuitumia. Ulifanya nini ili uwe na ujasiri wa uwezo wako wa kufanya mambo haya? Kuwa maalum.

... kwa msaada fulani. Hii lazima kushughulikiwa haraka kwa sababu mada huna bwana kuwa mashimo katika barabara yako ya mafanikio. Katika hesabu, kila mada hujenga juu ya kazi ya awali. Ni muhimu kuhakikisha kuwa na msingi imara kabla ya kuendelea.

Nani unaweza kuomba msaada? Washiriki wenzako na mwalimu ni rasilimali nzuri. Je, kuna mahali kwenye chuo ambapo waalimu hisabati zinapatikana? Je, ujuzi wako wa kujifunza unaweza kuboreshwa?

... hakuna-siipati! Hii ni ishara ya onyo na haipaswi kupuuza. Unapaswa kupata msaada mara moja au utazidiwa haraka. Angalia mwalimu wako haraka iwezekanavyo kujadili hali yako. Pamoja unaweza kuja na mpango wa kupata msaada unayohitaji.

Wachangiaji na Majina

• Template:ContribOpenStaxPreAlgebra