7.5: Mali ya Identity, Inverses, na Zero
- Page ID
- 173305
- Tambua mali ya utambulisho wa kuongeza na kuzidisha
- Tumia mali inverse ya kuongeza na kuzidisha
- Tumia mali ya sifuri
- Kurahisisha maneno kwa kutumia mali ya utambulisho, inverses, na sifuri
Kabla ya kuanza, fanya jaribio hili la utayari.
- Pata kinyume cha -4. Ikiwa umekosa tatizo hili, tathmini Mfano 3.1.3.
- Kupata kurudisha ya\(\dfrac{5}{2}\). Kama amekosa tatizo hili, mapitio Mfano 4.4.11.
- Kuzidisha:\(\dfrac{3a}{5} \cdot \dfrac{9}{2a}\). Ikiwa umekosa tatizo hili, kagua Mfano 4.3.9.
Tambua Mali ya Utambulisho wa Kuongeza na Kuzidisha
Nini kinatokea wakati sisi kuongeza sifuri kwa idadi yoyote? Kuongeza sifuri haina mabadiliko ya thamani. Kwa sababu hii, tunaita 0 utambulisho wa kuongezea. Kwa mfano,
\[\begin{split} 13 + 0 \qquad -14 &+ 0 \qquad 0 + (-3x) \\ 13 \qquad \qquad -&14 \qquad \; -3x \end{split}\]
mali ya utambulisho wa kuongeza: kwa yoyote halisi idadi a,
\[a + 0 = a \qquad 0 + a = a\]
0 inaitwa utambulisho wa kuongezea
mali ya utambulisho wa kuzidisha: kwa idadi yoyote halisi
\[a \cdot 1 = a \qquad 1 \cdot a = a\]
1 inaitwa utambulisho wa kuzidisha
Tambua kama kila equation inaonyesha mali ya utambulisho wa kuongeza au kuzidisha. (a) 7 + 0 = 7 (b) -16 (1) = -16
Suluhisho
(a) 7 + 0 = 7
| Tunaongeza 0. | Sisi ni kutumia mali ya utambulisho wa kuongeza. |
(b) -16 (1) = -16
| Sisi ni kuzidisha kwa 1. | Tunatumia mali ya utambulisho wa kuzidisha. |
Tambua kama kila equation inaonyesha mali ya utambulisho wa kuongeza au kuzidisha: (a) 23 + 0 = 23 (b) -37 (1) = -37.
- Jibu
-
utambulisho mali ya kuongeza
- Jibu b
-
utambulisho mali ya kuzidisha
Tambua kama kila equation inaonyesha mali ya utambulisho wa kuongeza au kuzidisha: (a) 1 • 29 = 29 (b) 14 + 0 = 14.
- Jibu
-
utambulisho mali ya kuzidisha
- Jibu b
-
utambulisho wa nyongeza
Tumia Mali ya Inverse ya Kuongeza na Kuzidisha
Nini idadi aliongeza kwa 5 anatoa livsmedelstillsats utambulisho, 0?
| 5 + _____ = 0 | Tunajua\(5 + (\textcolor{red}{-5}) = 0\) |
Nini idadi aliongeza kwa -6 anatoa livsmedelstillsats utambulisho, 0?
| -6 + _____ = 0 | Tunajua\(-6 + (\textcolor{red}{6}) = 0\) |
Angalia kwamba katika kila kesi, idadi ya kukosa ilikuwa kinyume na idadi. Tunaita -a nyongeza inverse ya. kinyume cha idadi ni nyongeza yake inverse. Nambari na kinyume chake huongeza 0, ambayo ni utambulisho wa kuongezea.
Nini idadi tele na\(\dfrac{2}{3}\) anatoa utambulisho multiplicative, 1? Kwa maneno mengine, mara theluthi mbili nini matokeo katika 1?
| \(\dfrac{2}{3} \cdot\)_____ = 1 | Tunajua\(\dfrac{2}{3} \cdot \textcolor{red}{\dfrac{3}{2}} = 1\) |
Nambari gani imeongezeka kwa 2 inatoa utambulisho wa kuzidisha, 1? Kwa maneno mengine mara mbili nini matokeo katika 1?
| 2 • _____ = 1 | Tunajua\(2 \cdot \textcolor{red}{\dfrac{1}{2}} = 1\) |
Angalia kwamba katika kila kesi, nambari iliyopo ilikuwa ya usawa wa idadi.
Tunaita inverse\(\dfrac{1}{a}\) ya kuzidisha ya a (a 坪 0). Utoaji wa nambari ni inverse yake ya kuzidisha. Nambari na kuongezeka kwake kwa mara kwa mara hadi 1, ambayo ni utambulisho wa kuzidisha.
Tutaweza rasmi hali ya Inverse Mali hapa:
Inverse Mali ya Aidha kwa yoyote ya kweli idadi a,
\[a + (−a) = 0\]
-a ni inverse livsmedelstillsats ya a.
Inverse Mali ya Kuzidisha kwa idadi yoyote halisi a 坪 0,
\[a \cdot \dfrac{1}{a} = 1\]
\(\dfrac{1}{a}\)ni inverse multiplicative ya.
Pata inverse ya nyongeza ya kila kujieleza: (a) 13 (b)\(− \dfrac{5}{8}\) (c) 0.6.
Suluhisho
Ili kupata inverse ya kuongezea, tunapata kinyume.
- Inverse ya nyongeza ya 13 ni kinyume chake, -13.
- Inverse ya kuongezea\(− \dfrac{5}{8}\) ni kinyume chake,\(\dfrac{5}{8}\).
- Inverse ya kuongezea ya 0.6 ni kinyume chake, -0.6.
Pata inverse ya nyongeza ya kila kujieleza: (a) 18 (b)\(\dfrac{7}{9}\) (c) 1.2.
- Jibu
-
\(-18\)
- Jibu b
-
\(-\frac{7}{9}\)
- Jibu c
-
\(-1.2\)
Pata inverse ya nyongeza ya kila kujieleza: (a) 47 (b)\(\dfrac{7}{13}\) (c) 8.4.
- Jibu
-
\(-47\)
- Jibu b
-
\(-\frac{7}{13}\)
- Jibu c
-
\(-8.4\)
Pata inverse ya kuzidisha: (a) 9 (b)\(− \dfrac{1}{9}\) (c) 0.9.
Suluhisho
Ili kupata inverse ya kuongezea, tunapata kinyume.
- Inverse ya kuzidisha ya 9 ni ya usawa wake,\(\dfrac{1}{9}\).
- Inverse ya kuzidisha\(− \dfrac{1}{9}\) ni ya usawa wake, -9.
- Ili kupata inverse ya kuzidisha ya 0.9, sisi kwanza kubadilisha 0.9 kwa sehemu,\(\dfrac{9}{10}\). Kisha tunapata usawa,\(\dfrac{10}{9}\).
Pata inverse ya kuzidisha: (a) 5 (b)\(− \dfrac{1}{7}\) (c) 0.3.
- Jibu
-
\(\frac{1}{5}\)
- Jibu b
-
\(-7\)
- Jibu c
-
\(\frac{10}{3}\)
Pata inverse ya kuzidisha: (a) 18 (b)\(− \dfrac{4}{5}\) (c) 0.6.
- Jibu
-
\(\frac{1}{18}\)
- Jibu b
-
\(-\frac{5}{4}\)
- Jibu c
-
\(\frac{5}{3}\)
Tumia Mali ya Zero
Tayari tumejifunza kuwa sifuri ni utambulisho wa kuongezea, kwani inaweza kuongezwa kwa nambari yoyote bila kubadilisha utambulisho wa nambari. Lakini sifuri pia ina mali maalum linapokuja kuzidisha na mgawanyiko.
Kuzidisha kwa sifuri
Ni nini kinachotokea unapozidisha idadi kwa 0? Kuongezeka kwa 0 hufanya bidhaa sawa na sifuri. Bidhaa ya idadi yoyote halisi na 0 ni 0.
Kwa yoyote ya kweli idadi a,
\[a \cdot 0 = 0 \qquad 0 \cdot a = 0\]
Kurahisisha: (a) -8 • 0 (b)\(\dfrac{5}{12} \cdot 0\) (c) 0 (2.94).
Suluhisho
(a) -8 • 0
| Bidhaa ya idadi yoyote halisi na 0 ni 0. | 0 |
(b)\(\dfrac{5}{12} \cdot 0\)
| Bidhaa ya idadi yoyote halisi na 0 ni 0. | 0 |
(c) 0 (2.94)
| Bidhaa ya idadi yoyote halisi na 0 ni 0. | 0 |
Kurahisisha: (a) -14 • 0 (b)\(0 \cdot \dfrac{2}{3}\) (c) (16.5) • 0.
- Jibu
-
\(0\)
- Jibu b
-
\(0\)
- Jibu c
-
\(0\)
Kurahisisha: (a) (1.95) • 0 (b) 0 (-17) (c)\(0 \cdot \dfrac{5}{4}\).
- Jibu
-
\(0\)
- Jibu b
-
\(0\)
- Jibu c
-
\(0\)
Kugawanya na Zero
Nini kuhusu kugawa na 0? Fikiria juu ya mfano halisi: ikiwa hakuna vidakuzi kwenye jar ya kuki na watu watatu wanataka kuwashirikisha, ni vidakuzi ngapi ambavyo kila mtu atapata? Kuna cookies 0 kushiriki, hivyo kila mtu anapata cookies 0.
\[0 \div 3 = 0\]
Kumbuka kwamba tunaweza daima kuangalia mgawanyiko na kuhusiana kuzidisha ukweli. Kwa hiyo, tunajua kwamba
\[0 \div 3 = 0\; because\; 0 \cdot 3 = 0 \ldotp\]
Kwa idadi yoyote halisi, ila 0,\(\dfrac{0}{a}\) = 0 na 0 ÷ = 0.
Zero imegawanywa na idadi yoyote halisi isipokuwa sifuri ni sifuri.
Kurahisisha: (a) 0 ÷ 5 (b)\(\dfrac{0}{−2}\) (c) 0 ÷\(\dfrac{7}{8}\).
Suluhisho
(a) 0 ÷ 5
| Zero kugawanywa na idadi yoyote halisi, ila 0, ni sifuri. | 0 |
(b)\(\dfrac{0}{−2}\)
| Zero kugawanywa na idadi yoyote halisi, ila 0, ni sifuri. | 0 |
(c) 0 ÷\(\dfrac{7}{8}\)
| Zero kugawanywa na idadi yoyote halisi, ila 0, ni sifuri. | 0 |
Kurahisisha: (a) 0 ÷ 11 (b)\(\dfrac{0}{−6}\) (c) 0 ÷\(\dfrac{3}{10}\).
- Jibu
-
\(0\)
- Jibu b
-
\(0\)
- Jibu c
-
\(0\)
Kurahisisha: (a) 0 ÷\(\dfrac{8}{3}\) (b) 0 ÷ (-10) (c) 0 ÷ 12.75.
- Jibu
-
\(0\)
- Jibu b
-
\(0\)
- Jibu c
-
\(0\)
Sasa hebu fikiria juu ya kugawa idadi kwa sifuri. Matokeo ya kugawa 4 na 0 ni nini? Fikiria juu ya ukweli unaohusiana na kuzidisha. Je, kuna idadi kwamba tele kwa 0 anatoa 4?
4 ÷ 0 = ___ inamaanisha ___ • 0 = 4
Kwa kuwa idadi yoyote halisi tele kwa 0 sawa 0, hakuna idadi halisi ambayo inaweza kuzidishwa na 0 kupata 4. Tunaweza kuhitimisha kuwa hakuna jibu la 4 ÷ 0, na hivyo tunasema kuwa mgawanyiko na sifuri haujafafanuliwa.
Kwa idadi yoyote halisi a,\(\dfrac{a}{0}\), na ÷ 0 haijulikani.
Idara na sifuri haijulikani.
Kurahisisha: (a) 7.5 ÷ 0 (b)\(\dfrac{−32}{0}\) (c)\(\dfrac{4}{9}\) ÷ 0.
Suluhisho
(a) 7.5 ÷ 0
| Idara na sifuri haijulikani. | haijafafanuliwa |
(b)\(\dfrac{−32}{0}\)
| Idara na sifuri haijulikani. | haijafafanuliwa |
(c)\(\dfrac{4}{9}\) ÷ 0
| Idara na sifuri haijulikani. | haijafafanuliwa |
Kurahisisha: (a) 16.4 ÷ 0 (b)\(\dfrac{−2}{0}\) (c)\(\dfrac{1}{5}\) ÷ 0.
- Jibu
-
haijafafanuliwa
- Jibu b
-
haijafafanuliwa
- Jibu c
-
haijafafanuliwa
Kurahisisha:\(\dfrac{−5}{0}\) (a) (b) 96.9 ÷ 0 (c)\(\dfrac{4}{15}\) ÷ 0.
- Jibu
-
haijafafanuliwa
- Jibu b
-
haijafafanuliwa
- Jibu c
-
haijafafanuliwa
Sisi muhtasari mali ya sifuri.
Kuzidisha na Zero: Kwa yoyote ya kweli idadi a,
\[a \cdot 0 = 0 \qquad 0 \cdot a = 0\]
Bidhaa ya namba yoyote na 0 ni 0.
Idara na Zero: Kwa yoyote ya kweli idadi a, a ∙ 0
\[\dfrac{0}{a} = 0\]
Zero imegawanywa na idadi yoyote halisi, isipokuwa yenyewe, ni sifuri.
\[\dfrac{a}{0}\; is\; undefined \ldotp\]
Idara na sifuri haijulikani.
Kurahisisha Maneno kwa kutumia Mali ya Utambulisho, Inverses, na Zero
Sasa tutatumia kutumia mali ya utambulisho, inverses, na sifuri ili kurahisisha maneno.
Kurahisisha: 3x + 15 - 3x.
Suluhisho
| Angalia inverses livsmedelstillsats, 3x na -3x. | 0 + 15 |
| Ongeza. | 15 |
Kurahisisha: -12z + 9 + 12z.
- Jibu
-
9
Kurahisisha: -25u - 18 + 25u.
- Jibu
-
-18
Kurahisisha: 4 (0.25q).
Suluhisho
| Regroup, kwa kutumia mali associative. | [4 (0.25)] q |
| Kuzidisha. | 1.00q |
| Kurahisisha; 1 ni utambulisho multiplicative. | q |
Kurahisisha: 2 (0.5p).
- Jibu
-
p
Kurahisisha: 25 (0.04r).
- Jibu
-
r
Kurahisisha:\(\dfrac{0}{n + 5}\), ambapo n Δ -5.
Suluhisho
| Zero imegawanywa na idadi yoyote halisi isipokuwa yenyewe ni sifuri. | 0 |
Kurahisisha:\(\dfrac{0}{m + 7}\), ambapo m -7.
- Jibu
-
0
Kurahisisha:\(\dfrac{0}{d - 4}\), ambapo d Δ 4.
- Jibu
-
0
Kurahisisha:\(\dfrac{10 − 3p}{0}\).
Suluhisho
| Idara na sifuri haijulikani. | haijafafanuliwa |
Kurahisisha:\(\dfrac{18 − 6c}{0}\).
- Jibu
-
haijafafanuliwa
Kurahisisha:\(\dfrac{15 − 4q}{0}\).
- Jibu
-
haijafafanuliwa
kurahisisha:\(\dfrac{3}{4} \cdot \dfrac{4}{3}\) (6x + 12).
Suluhisho
Hatuwezi kuchanganya maneno katika mabano, kwa hiyo tunazidisha sehemu mbili kwanza.
| Kuzidisha; bidhaa ya kurudi ni 1. | 1 (6x + 12) |
| Kurahisisha kwa kutambua utambulisho multiplicative. | 6x 12 |
Kurahisisha:\(\dfrac{2}{5} \cdot \dfrac{5}{2}\) (20y+ 50).
- Jibu
-
20y + 50
Kurahisisha:\(\dfrac{3}{8} \cdot \dfrac{8}{3}\) (12z+ 16).
- Jibu
-
12z + 16
Mali yote ya namba halisi tumetumia katika sura hii ni muhtasari katika Jedwali\(\PageIndex{1}\).
| Mali | Ya Aidha | Ya kuzidisha |
|---|---|---|
| Mali ya kubadilisha | ||
| Ikiwa na b ni namba halisi basi... | a + b = b + a | a • b = b • a |
| Associative Mali | ||
| Ikiwa a, b, na c ni namba halisi basi... | (a + b) + c = a + (b + c) | (a • b) • c = (b • c) |
| Mali ya Identity | 0 ni utambulisho wa kuongezea | 1 ni utambulisho wa kuzidisha |
| Kwa yoyote ya kweli idadi a, |
a + 0 = a 0 + a = a |
a • 1 = a 1 • a = a |
| Inverse Mali | -a ni inverse ya nyongeza ya |
a, η 0 1/a ni inverse multiplicative ya |
| Kwa yoyote ya kweli idadi a, | a + (-a) = 0 | a • 1/a = 1 |
| Mali ya Kusambaza | ||
| Ikiwa a, b, c ni namba halisi, basi (b + c) = ab + ac | ||
| Mali ya Zero | ||
| Kwa yoyote ya kweli idadi a, |
a • 0 = 0 0 • a = 0 |
|
| Kwa yoyote halisi idadi a ambapo 0 |
\(\dfrac{0}{a} = 0\) \(\dfrac{a}{0}\)haijafafanuliwa |
|
Mazoezi hufanya kamili
Tambua Mali ya Utambulisho wa Kuongeza na Kuzidisha
Katika mazoezi yafuatayo, tambua kama kila mfano unatumia mali ya utambulisho wa kuongeza au kuzidisha.
- 101 + 0 = 101
- \(\dfrac{3}{5}(1) = \dfrac{3}{5}\)
- -9 • 1 = -9
- 0 + 64 = 64
Tumia Mali ya Inverse ya Kuongeza na Kuzidisha
Katika mazoezi yafuatayo, tafuta inverse ya kuzidisha.
- 8
- 14
- -17
- 19-19
- \(\dfrac{7}{12}\)
- \(\dfrac{8}{13}\)
- \(− \dfrac{3}{10}\)
- \(− \dfrac{5}{12}\)
- 0.8
- 0.4
- -0.2
- -0.5
Tumia Mali ya Zero
Katika mazoezi yafuatayo, kurahisisha kutumia mali ya sifuri.
- 48 • 0
- \(\dfrac{0}{6}\)
- \(\dfrac{3}{0}\)
- 22 • 0
- 0 ÷\(\dfrac{11}{12}\)
- \(\dfrac{6}{0}\)
- \(\dfrac{0}{3}\)
- 0 ÷\(\dfrac{7}{15}\)
- 0 •\(\dfrac{8}{15}\)
- (-3.14) (0)
- 5.72 ÷ 0
- \(\dfrac{\dfrac{1}{10}}{0}\)
Kurahisisha Maneno kwa kutumia Mali ya Utambulisho, Inverses, na Zero
Katika mazoezi yafuatayo, kurahisisha kutumia mali ya utambulisho, inverses, na sifuri.
- 19a + 44 - 19a
- 27c + 16 - 27c
- 38 + 11r - 38
- 29+ 31s - 92
- 10 (0.1d)
- 100 (0.01p)
- 5 (0.6q)
- 40 (0.05n)
- \(\dfrac{0}{r + 20}\), ambapo r ∙ -20
- \(\dfrac{0}{s + 13}\), ambapo s -13-13
- \(\dfrac{0}{u − 4.99}\), ambapo u ∙ 4.99
- \(\dfrac{0}{v − 65.1}\), ambapo v ∙ 65.1
- 0 ÷\(\left(x − \dfrac{1}{2}\right)\), wapi x Δ\(\dfrac{1}{2}\)
- 0 ÷\(\left(y − \dfrac{1}{6}\right)\), wapi y Δ\(\dfrac{1}{6}\)
- \(\dfrac{32 − 5a}{0}\), ambapo 32 - 5a ∙ 0
- \(\dfrac{28 − 9b}{0}\), ambapo 28 - 9b ∙ 0
- \(\dfrac{2.1 + 0.4c}{0}\), ambapo 2.1 + 0.4c Δ 0
- \(\dfrac{1.75 + 9 f}{0}\), ambapo 1.75 + 9 f Δ 0
- \(\left\dfrac{3}{4} + \dfrac{9}{10}m \right) \div 0\), wapi\(\dfrac{3}{4} + \dfrac{9}{10}m \neq 0\)
- \(\left(\dfrac{5}{16}n − \dfrac{3}{7}\right) \div 0\), wapi\(\dfrac{5}{16}n − \dfrac{3}{7} \neq 0\)
- \(\dfrac{9}{10} \cdot \dfrac{10}{9}\)(18p - 21)
- \(\dfrac{5}{7} \cdot \dfrac{7}{5}\)(20q - 35)
- 15\(\cdot \dfrac{3}{5}\) (4d + 10)
- 18\(\cdot \dfrac{5}{6}\) (15h + 24)
kila siku Math
- Malipo ya bima Carrie alikuwa na kujaza 5 kufanyika. Kila kujaza gharama $80. Bima yake ya meno ilimtaka kulipa 20% ya gharama. Tumia gharama ya Carrie
- kwa kutafuta copay yake kwa ajili ya kujaza kila, kisha kutafuta gharama yake ya jumla kwa ajili ya fillings 5, na
- kwa kuzidisha 5 (0.20) (80).
- Ni ipi kati ya Mali ya Hesabu Halisi uliyotumia kwa sehemu (b)?
- Kupika wakati Helen kununuliwa 24-pauni Uturuki kwa ajili ya familia yake Shukrani chakula cha jioni na anataka kujua ni muda gani wa kuweka Uturuki katika tanuri. Anataka kuruhusu 20 dakika kwa pauni wakati kupikia.
- Tumia urefu wa muda unaohitajika kuchoma Uturuki kwa kuzidisha 24 · 20 ili kupata idadi ya dakika na kisha kuzidisha bidhaa kwa 1 60 ili kubadilisha dakika ndani ya masaa.
- Kuzidisha 24\(\left(20 \cdot \dfrac{1}{60}\right)\).
- Ni ipi kati ya Mali ya Hesabu halisi inakuwezesha kuzidisha 24\(\left(20 \cdot \dfrac{1}{60}\right)\) badala ya (24 • 20)\(\dfrac{1}{60}\)?
Mazoezi ya kuandika
- Kwa maneno yako mwenyewe, kuelezea tofauti kati ya inverse ya kuongezea na inverse ya kuzidisha ya idadi.
- Je! Matumizi ya mali ya namba halisi yanawezaje iwe rahisi kurahisisha maneno?
Self Check
(a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
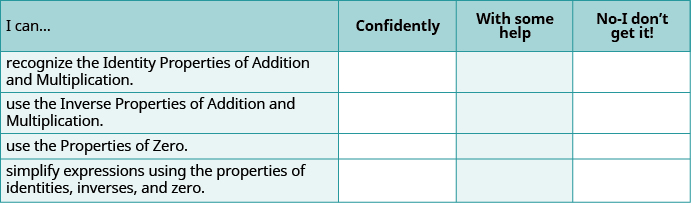
(b) Kwa kiwango cha 1—10, ungewezaje kupima ujuzi wako wa sehemu hii kwa kuzingatia majibu yako kwenye orodha? Unawezaje kuboresha hii?


