Skip to main content
Global

5.7: Tatua equations na Decimals

  1. Last updated
  2. Save as PDF
  • Page ID
    173438

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Kuamua kama decimal ni suluhisho la equation
    • Tatua equations na decimals
    • Tafsiri kwa equation na kutatua
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Tathmini x +\(\dfrac{2}{3}\) wakati x =\(− \dfrac{1}{4}\). Kama amekosa tatizo hili, mapitio Mfano 4.9.15.
    2. Tathmini 15 - y wakati y = -5. Ikiwa umekosa tatizo hili, tathmini Mfano 3.6.12.
    3. Kutatua\(\dfrac{n}{−7}\) = 42. Ikiwa umekosa tatizo hili, tathmini Mfano 4.12.5.

    Kuamua Kama Decimal ni Suluhisho la Equation

    Kutatua equations na decimals ni muhimu katika maisha yetu ya kila siku kwa sababu fedha ni kawaida imeandikwa na decimals. Wakati programu zinahusisha pesa, kama vile ununuzi mwenyewe, kufanya bajeti ya familia yako, au kupanga mipango ya baadaye ya biashara yako, utakuwa kutatua equations na decimals.

    Sasa kwa kuwa tumefanya kazi na decimals, tuko tayari kupata ufumbuzi wa equations kuwashirikisha decimals. Hatua tunazochukua ili kuamua kama namba ni suluhisho la equation ni sawa kama suluhisho ni namba nzima, integer, sehemu, au decimal. Tutaweza orodha hatua hizi hapa tena kwa ajili ya kumbukumbu rahisi.

    JINSI YA: TAMBUA KAMA NAMBARI NI SULUHISHO LA EQUATION
    • Hatua ya 1. Badilisha idadi ya kutofautiana katika equation.
    • Hatua ya 2. Kurahisisha maneno pande zote mbili za equation.
    • Hatua ya 3. Kuamua kama equation kusababisha ni kweli.
      • Ikiwa ndivyo, nambari ni suluhisho.
      • Ikiwa sio, nambari sio suluhisho.
    Mfano\(\PageIndex{1}\):

    Kuamua kama kila moja ya yafuatayo ni suluhisho la x - 0.7 = 1.5: (a) x = 1 (b) x = -0.8 (c) x = 2.2

    Suluhisho

    (a) x - 0.7 = 1.5

    Mbadala\(\textcolor{red}{1}\) kwa ajili ya x. $$\ textcolor {nyekundu} {1} - 0.7\ stackrel {?} {=} 1.5$
    Ondoa. $0.3\ mpya 1.5$ $

    Kwa kuwa x = 1 haina kusababisha equation kweli, 1 si suluhisho la equation.

    (b) x - 0.7 = 1.5

    Mbadala\(\textcolor{red}{-0.8}\) kwa ajili ya x. $$\ textcolor {nyekundu} {-0.8} - 0.7\ stackrel {?} {=} 1.5$
    Ondoa. $-1.5\ mpya $1.5$

    Kwa kuwa x = -0.8 haina kusababisha equation ya kweli, -0.8 si suluhisho la equation.

    (c) x - 0.7 = 1.5

    Mbadala\(\textcolor{red}{2.2}\) kwa ajili ya x. $$\ textcolor {nyekundu} {2.2} - 0.7\ stackrel {?} {=} 1.5$
    Ondoa. $1.5 = 1.5\;\ checkmark$$

    Kwa kuwa x = 2.2 matokeo katika equation ya kweli, 2.2 ni suluhisho la equation.

    Zoezi\(\PageIndex{1}\):

    Kuamua kama kila thamani ni suluhisho la equation iliyotolewa. x - 0.6 = 1.3: (a) x = 0.7 (b) x = 1.9 (c) x = -0.7

    Jibu

    hapana

    Jibu b

    ndiyo

    Jibu c

    hapana

    Zoezi\(\PageIndex{2}\):

    Kuamua kama kila thamani ni suluhisho la equation iliyotolewa. y - 0.4 = 1.7: (a) y = 2.1 (b) y = 1.3 (c) -1.3

    Jibu

    ndiyo

    Jibu b

    hapana

    Jibu c
    hapana

    Kutatua Equations na Decimals

    Katika sura zilizopita, tulitatua equations kwa kutumia Mali ya Usawa. Tutatumia mali hizi sawa kutatua equations na decimals.

    Mali ya Usawa

    Ondoa Mali ya Usawa

    Kwa idadi yoyote a, b, na c, Kama = b, basi - c = b - c.

    Kuongeza Mali ya Usawa

    Kwa idadi yoyote a, b, na c, Kama = b, basi a + c = b + c.

    Idara ya Mali ya Usawa

    Kwa idadi yoyote a, b, na c, na c - 0 Kama = b, basi\(\dfrac{a}{c} = \dfrac{b}{c}\)

    Mali ya kuzidisha ya Usawa

    Kwa idadi yoyote a, b, na c, Ikiwa = b, basi ac = bc

    Unapoongeza, ondoa, kuzidisha au ugawanye kiasi sawa kutoka pande zote mbili za equation, bado una usawa.

    Mfano\(\PageIndex{2}\):

    Tatua: y + 2.3 = -4.7.

    Suluhisho

    Tutatumia Mali ya Kuondoa ya Usawa ili kutenganisha kutofautiana.

    Ondoa\(\textcolor{red}{2.3}\) kutoka kila upande, ili uondoe kuongeza. $$y + 2.3\ rangi ya maandishi {nyekundu} {-2.3} = -4.7\ rangi ya maandishi {nyekundu} {-2.3} $$
    Kurahisisha. $y = -$7 $

    Angalia:

    Mbadala y =\(\textcolor{red}{-7}\). $$\ textcolor {nyekundu} {-7} + 2.3\ stackrel {?} {=} -4.7 $$
    Kurahisisha. $$-4.7 = -4.7\;\ alama ya $$

    Kwa kuwa y = -7 hufanya y + 2.3 = -4.7 kauli ya kweli, tunajua tumepata suluhisho la equation hii.

    Zoezi\(\PageIndex{3}\):

    Tatua: y + 2.7 = -5.3.

    Jibu

    \(y=-8\)

    Zoezi\(\PageIndex{4}\):

    Tatua: y + 3.6 = -4.8.

    Jibu

    \(y=-8.4\)

    Mfano\(\PageIndex{3}\):

    Tatua: a - 4.75 = -1.39.

    Suluhisho

    Tutatumia Mali ya Kuongeza ya Usawa.

    Ongeza 4.75 kwa kila upande, ili uondoe uondoaji. $$a - 4.75\ textcolor {nyekundu} {+4.75} = -1.39\ textcolor {nyekundu} {+4.75} $$
    Kurahisisha. $$a = 3.36 $$

    Angalia:

    Badilisha a =\(\textcolor{red}{3.36}\). $$\ textcolor {nyekundu} {3.36} - 4.75\ stackrel {?} {=} -1.39 $$
      $-1.39 = -1.39\;\ checkmark$$

    Kwa kuwa matokeo ni taarifa ya kweli, a = 3.36 ni suluhisho la equation.

    Zoezi\(\PageIndex{5}\):

    Tatua: a - 3.93 = -2.86.

    Jibu

    \(a=1.07\)

    Zoezi\(\PageIndex{6}\):

    Tatua: n - 3.47 = -2.64.

    Jibu

    \(n=0.83\)

    Mfano\(\PageIndex{4}\):

    Tatua: -4.8 = 0.8n.

    Suluhisho

    Tutatumia Idara ya Mali ya Usawa. Tumia Mali ya Usawa ili kupata thamani ya n.

    Lazima tugawanye pande zote mbili kwa 0.8 ili kutenganisha n. $$\ dfrac {-4.8} {\ textcolor {nyekundu} {0.8}} =\ dfrac {0.8n} {\ textcolor {nyekundu} {08}} $$
    Kurahisisha. $-6 = n $$

    Angalia:

    Mbadala n =\(\textcolor{red}{-6}\). $-4.8\ stackrel {?} {=} 0.8 (\ textcolor {nyekundu} {-6}) $$
      $$-4.8 = -4.8\;\ alama $$

    Kwa kuwa n = -6 hufanya -4.8 = 0.8n kauli ya kweli, tunajua tuna suluhisho.

    Zoezi\(\PageIndex{7}\):

    Tatua: -8.4 = 0.7b.

    Jibu

    \(b=-12\)

    Zoezi\(\PageIndex{8}\):

    Tatua: -5.6 = 0.7c.

    Jibu

    \(c=-8\)

    Mfano\(\PageIndex{5}\):

    Tatua:\(\dfrac{p}{−1.8}\) = -6.5.

    Suluhisho

    Tutatumia Mali ya kuzidisha ya Usawa.

    Hapa, p imegawanywa na -1.8. Lazima tuzidishe na -1.8 ili kutenganisha p. $$\ textcolor {nyekundu} {-1.8}\ kushoto (\ dfrac {p} {-1.8}\ haki) =\ textcolor {nyekundu} {-1.8} (-6.5) $$
    Kuzidisha. $$p = 11.7$$

    Angalia:

    Mbadala p =\(\textcolor{red}{11.7}\). $$\ dfrac {\ textcolor {nyekundu} {11.7}} {-1.8}\ stackrel {?} {=} -6.5$$
      $-6.5 = -6.5\;\ checkmark $$

    Suluhisho la\(\dfrac{p}{−1.8}\) = -6.5 ni p = 11.7.

    Zoezi\(\PageIndex{9}\):

    Tatua:\(\dfrac{c}{−2.6}\) = -4.5.

    Jibu

    \(c=-11.7\)

    Zoezi\(\PageIndex{10}\):

    Tatua:\(\dfrac{b}{−1.2}\) = -5.4.

    Jibu

    \(b=6.48\)

    Tafsiri kwa Equation na Kutatua

    Sasa kwa kuwa tumetatua equations na decimals, tuko tayari kutafsiri sentensi za neno kwa equations na kutatua. Kumbuka kuangalia maneno na misemo inayoonyesha shughuli za kutumia.

    Mfano\(\PageIndex{6}\):

    Tafsiri na kutatua: Tofauti ya n na 4.3 ni 2.1.

    Suluhisho

    Tafsiri.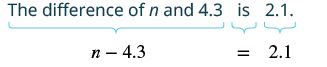
    Ongeza 4.3 kwa pande zote mbili za equation. $$n - 4.3\ textcolor {nyekundu} {+4.3} = 2.1\ rangi ya maandishi {nyekundu} {+4.3} $$
    Kurahisisha. $$n = 6.4$$

    Angalia:

    Hebu n = 6.4. Je, tofauti ya 6.4 na 4.3 ni sawa na 2.1?
    Tafsiri. $6.4 - 4.3\ stackrel {?} {=} 2.1 $$
    Kurahisisha. $2.1 = 2.1\;\ checkmark$$
    Zoezi\(\PageIndex{11}\):

    Tafsiri na kutatua: Tofauti ya y na 4.9 ni 2.8.

    Jibu

    \(y-4.9=2.8\);\(y=7.7\)

    Zoezi\(\PageIndex{12}\):

    Tafsiri na kutatua: Tofauti ya z na 5.7 ni 3.4.

    Jibu

    \(z-5.7=3.4\);\(z=9.1\)

    Mfano\(\PageIndex{7}\):

    Tafsiri na kutatua: Bidhaa ya -3.1 na x ni 5.27.

    Suluhisho

    Tafsiri.
    Gawanya pande zote mbili kwa -3.1. $$\ dfrac {-3.1x} {\ textcolor {nyekundu} {-3.1}} =\ dfrac {5.27} {\ textcolor {nyekundu} {-3.1}} $ $
    Kurahisisha. $$x = -1.7$$

    Angalia:

    Hebu x = -1.7. Je, bidhaa za -3.1 na -1.7 ni sawa na 5.27?
    Tafsiri. $-3.1 (-1.7)\ stackrel {?} {=} 5.27 $$
    Kurahisisha. $5.27 = 5.27\;\ checkmark $$
    Zoezi\(\PageIndex{13}\):

    Tafsiri na kutatua: Bidhaa ya -4.3 na x ni 12.04.

    Jibu

    \(-4.3x=12.04\);\(x=-2.8\)

    Zoezi\(\PageIndex{14}\):

    Tafsiri na kutatua: Bidhaa ya -3.1 na m ni 26.66.

    Jibu

    \(-3.1m=26.66\);\(m=-8.6\)

    Mfano\(\PageIndex{8}\):

    Tafsiri na kutatua: Quotient ya p na -2.4 ni 6.5.

    Suluhisho

    Tafsiri.
    Panua pande zote mbili kwa -2.4. $$\ textcolor {nyekundu} {-2.4}\ kushoto (\ dfrac {p} {-2.4}\ haki) =\ textcolor {nyekundu} {-2.4} (6.5) $$
    Kurahisisha. $$p = -15.6 $$

    Angalia:

    Hebu p = -15.6. Je, quotient ya -15.6 na -2.4 ni sawa na 6.5?
    Tafsiri. $$\ dfrac {\ textcolor {nyekundu} {-15.6}} {-2.4}\ stackrel {?} {=} 6.5$$
    Kurahisisha. $6.5 = 6.5\;\ checkmark$$
    Zoezi\(\PageIndex{15}\):

    Tafsiri na kutatua: Quotient ya q na -3.4 ni 4.5.

    Jibu

    \(\frac{1}{-3.4}=4.5\);\(q=-15.3\)

    Zoezi\(\PageIndex{16}\):

    Tafsiri na kutatua: Quotient ya r na -2.6 ni 2.5.

    Jibu

    \(\frac{r}{-2.6}=2.5\);\(r=-6.5\)

    Mfano\(\PageIndex{9}\):

    Tafsiri na kutatua: Jumla ya n na 2.9 ni 1.7.

    Suluhisho

    Tafsiri.
    Ondoa 2.9 kutoka kila upande. $$n + 2.9\ rangi ya maandishi {nyekundu} {-2.9} = 1.7\ rangi ya maandishi {nyekundu} {-2.9} $$
    Kurahisisha. $$n = -1.2 $$

    Angalia:

    Hebu n = -1.2. Je! Jumla -1.2 na 2.9 ni sawa na 1.7?
    Tafsiri. $-1.2 + 2.9\ stackrel {?} {=} 1.7$$
    Kurahisisha. $1.7 = 1.7\;\ checkmark$$
    Zoezi\(\PageIndex{17}\):

    Tafsiri na kutatua: Jumla ya j na 3.8 ni 2.6.

    Jibu

    \(j+3.8=2.6\);\(j=-1.2\)

    Zoezi\(\PageIndex{18}\):

    Tafsiri na kutatua: Jumla ya k na 4.7 ni 0.3.

    Jibu

    \(k+4.7=0.3\);\(k=-4.4\)

    PATA RASILIMALI ZA ZIADA

    Kutatua Equations Hatua moja Kuhusisha Decimals

    Tatua usawa wa Hatua moja na Decimals kwa Kuongeza na Kuondoa

    Tatua usawa wa Hatua moja na Decimals kwa Kuzidisha

    Kutatua Hatua moja Equation na Decimals kwa Kugawa

    Mazoezi hufanya kamili

    Kuamua Kama Decimal ni Suluhisho la Equation

    Katika mazoezi yafuatayo, onyesha kama kila namba ni suluhisho la equation iliyotolewa.

    1. x - 0.8 = 2.3
      1. x = 2
      2. x = -1.5
      3. x = 3.1
    2. y + 0.6 = -3.4
      1. y = -4
      2. y = -2.8
      3. y = 2.6
    3. \(\dfrac{h}{1.5}\)= -4.3
      1. h = 6.45
      2. h = -6.45
      3. h = -2.1
    4. 0.75k = -3.6
      1. k = -0.48
      2. k = -4.8
      3. k = -2.7

    Kutatua Equations na Decimals

    Katika mazoezi yafuatayo, tatua equation.

    1. y + 2.9 = 5.7
    2. m + 4.6 = 6.5
    3. f + 3.45 = 2.6
    4. h + 4.37 = 3.5
    5. a + 6.2 = -1.7
    6. b + 5.8 = -2.3
    7. c + 1.15 = -3.5
    8. d + 2.35 = -4.8
    9. n -2.6 = 1.8
    10. p - 3.6 = 1.7
    11. x - 0.4 = -3.9
    12. y - 0.6 = -4.5
    13. j -1.82 = -6.5
    14. k -3.19 = -4.6
    15. m - 0.25 = -1.67
    16. q - 0.47 = -1.53
    17. 0.5x = 3.5
    18. 0.4p = 9.2
    19. -1.7c = 8.5
    20. -2.9x = 5.8
    21. -1.4p = -4.2
    22. -2.8m = -8.4
    23. -120 = 1.5q
    24. -75 = 1.5y
    25. 0.24x = 4.8
    26. 0.18n = 5.4
    27. -3.4z = -9.18
    28. -2.7u = -9.72
    29. \(\dfrac{a}{0.4}\)= -20
    30. \(\dfrac{b}{0.3}\)= -9
    31. \(\dfrac{x}{0.7}\)= -0.4
    32. \(\dfrac{y}{0.8}\)= -0.7
    33. \(\dfrac{p}{−5}\)= -1.65
    34. \(\dfrac{q}{−4}\)= -5.92
    35. \(\dfrac{r}{−1.2}\)= -6
    36. \(\dfrac{s}{−1.5}\)= 1-3

    Mazoezi ya mchanganyiko

    Katika mazoezi yafuatayo, tatua equation. Kisha angalia suluhisho lako.

    1. x - 5 = -11
    2. \(− \dfrac{2}{5}\)= x + (\ dfrac {3} {4}\)
    3. p + 8 = —2
    4. p +\(\dfrac{2}{3} = \dfrac{1}{12}\)
    5. -4.2m = -33.6
    6. q + 9.5 = -14
    7. q +\(\dfrac{5}{6} = \dfrac{1}{12}\)
    8. \(\dfrac{8.6}{15}\)= - d
    9. \(\dfrac{7}{8} m = \dfrac{1}{10}\)
    10. \(\dfrac{j}{−6.2}\)= 1-3
    11. \(− \dfrac{2}{3}\)= y +\(\dfrac{3}{8}\)
    12. s - 1.75 = -3.2
    13. \(\dfrac{11}{20}\)= - f
    14. -3.6b = 2.52
    15. -4.2a = 3.36
    16. -9.1n = -63.7
    17. r -1.25 = -2.7
    18. \(\dfrac{1}{4} n = \dfrac{7}{10}\)
    19. \(\dfrac{h}{−3}\)= -8
    20. y - 7.82 = -16

    Tafsiri kwa Equation na Kutatua

    Katika mazoezi yafuatayo, kutafsiri na kutatua.

    1. Tofauti ya n na 1.9 ni 3.4.
    2. Tofauti n na 1.5 ni 0.8.
    3. Bidhaa ya -6.2 na x ni -4.96.
    4. Bidhaa ya -4.6 na x ni -3.22.
    5. Quotient ya y na -1.7 ni -5.
    6. Quotient ya z na -3.6 ni 3.
    7. Jumla ya n na -7.3 ni 2.4.
    8. Jumla ya n na -5.1 ni 3.8.

    kila siku Math

    1. Shawn alinunua jozi ya viatu kuuzwa kwa $78. Tatua equation 0.75p = 78 ili kupata bei ya awali ya viatu, p.
    2. Mary kununuliwa jokofu mpya. Bei ya jumla ikiwa ni pamoja na kodi ya mauzo ilikuwa $1,350. Pata bei ya rejareja, r, ya jokofu kabla ya kodi kwa kutatua equation 1.08r = 1,350.

    Mazoezi ya kuandika

    1. Fikiria juu ya kutatua equation 1.2y = 60, lakini si kweli kutatua. Je! Unafikiri ufumbuzi unapaswa kuwa mkubwa kuliko 60 au chini ya 60? Eleza hoja zako. Kisha kutatua equation kuona kama mawazo yako ilikuwa sahihi.
    2. Fikiria juu ya kutatua equation 0.8x = 200, lakini si kweli kutatua. Je! Unafikiri ufumbuzi unapaswa kuwa mkubwa kuliko 200 au chini ya 200? Eleza hoja zako. Kisha kutatua equation kuona kama mawazo yako ilikuwa sahihi.

    Self Check

    (a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

    (b) Kwa kiwango cha 1—10, ungewezaje kupima ujuzi wako wa sehemu hii kwa kuzingatia majibu yako kwenye orodha? Unawezaje kuboresha hii?

    Wachangiaji na Majina