Skip to main content
Global

5.6: Decimals na FRACTIONS (Sehemu ya 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    173445

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Pata mzunguko na Eneo la Mizunguko

    Mali ya miduara yamejifunza kwa zaidi ya miaka 2,000. Miduara yote ina sura sawa, lakini ukubwa wao huathiriwa na urefu wa radius, sehemu ya mstari kutoka katikati hadi hatua yoyote kwenye mduara. Sehemu ya mstari inayopita katikati ya mduara inayounganisha pointi mbili kwenye mduara inaitwa kipenyo. Kipenyo ni mara mbili kwa muda mrefu kama radius. Angalia Kielelezo\(\PageIndex{1}\).

    Ukubwa wa mduara unaweza kupimwa kwa njia mbili. Umbali unaozunguka mduara huitwa mduara wake.

    Mduara unaonyeshwa. Mstari wa dotted unaoendesha kupitia sehemu pana zaidi ya mduara umeandikwa kama kipenyo. Mstari wa dotted kutoka katikati ya mduara hadi kwenye mduara umeandikwa kama radius. Kando ya mduara ni mduara.

    Kielelezo\(\PageIndex{1}\)

    Archimedes aligundua kuwa kwa miduara ya ukubwa tofauti, kugawanya mzunguko na kipenyo daima hutoa idadi sawa. Thamani ya nambari hii ni pi, iliyoonyeshwa na barua ya Kigiriki\(\pi\) (pie inayojulikana). Hata hivyo, thamani halisi ya\(\pi\) haiwezi kuhesabiwa tangu decimal haijaisha au kurudia (tutajifunza zaidi kuhusu idadi kama hii katika Mali ya Hesabu halisi.)

    Ikiwa tunataka mzunguko halisi au eneo la mduara, tunaacha ishara\(\pi\) katika jibu. Tunaweza kupata jibu takriban kwa kubadilisha 3.14 kama thamani ya\(\pi\). Tunatumia ishara ≈ kuonyesha kwamba matokeo ni takriban, sio sahihi.

    Kumbuka: Mali ya Mizunguko

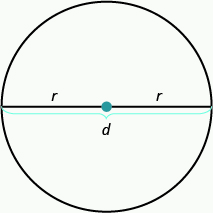
    Mduara unaonyeshwa. Mstari unaendesha kupitia sehemu pana zaidi ya mduara. Kuna dot nyekundu katikati ya mduara. nusu ya mstari kutoka katikati ya mduara kwa uhakika upande wa kulia wa mduara ni kinachoitwa na r. nusu ya mstari kutoka katikati ya mduara kwa uhakika upande wa kushoto wa mduara pia kinachoitwa na r. sehemu mbili kinachoitwa r na brace inayotolewa chini kuonyesha kwamba sehemu nzima ni kinachoitwa d.

    r ni urefu wa radius.

    d ni urefu wa kipenyo.

    Mzunguko ni 2\(\pi\) r.\[C = 2 \pi r\]

    Eneo ni\(\pi\) r 2. \[A = \pi r^{2}\]

    Kwa kuwa kipenyo ni mara mbili ya radius, njia nyingine ya kupata mzunguko ni kutumia formula C =\(\pi\) d.

    Tuseme tunataka kupata eneo halisi la mduara wa inchi 10 za radius. Ili kuhesabu eneo hilo, tunataka kutathmini formula kwa eneo wakati r = 10 inchi na kuacha jibu kwa suala la\(\pi\).

    \[\begin{split} A & = \pi r^{2} \\ A & = \pi (10^{2}) \\ A & = \pi \cdot 100 \end{split}\]

    Tunaandika\(\pi\) baada ya 100. Hivyo thamani halisi ya eneo ni A = 100 inchi\(\pi\) za mraba. Ili takriban eneo hilo, tunaweza kubadilisha\(\pi\) ≈ 3.14.

    \[\begin{split} A & = 100 \pi \\ & \approx 100 \cdot 3.14 \\ & \approx 314\; square\; inches \end{split}\]

    Kumbuka kutumia vitengo vya mraba, kama vile inchi za mraba, unapohesabu eneo hilo.

    Mfano\(\PageIndex{10}\):

    Mduara una radius sentimita 10. Takriban (a) mzunguko na (b) eneo.

    Suluhisho

    (a) Kupata mduara wakati r = 10.

    Andika formula ya mzunguko. C = 2\(\pi\) r
    badala 3.14 kwa\(\pi\) na 10 kwa r. C ≈ 2 (3.14) (10)
    Kuzidisha. C ≈ 62.8 sentimita

    (b) Pata eneo wakati r = 10.

    Andika formula kwa eneo. A =\(\pi\) r 2
    badala 3.14 kwa\(\pi\) na 10 kwa r. A ≈ (3.14) (10) 2
    Kuzidisha. A ≈ 314 sentimita za mraba
    Zoezi\(\PageIndex{19}\):

    Mduara una radius inchi 50. Takriban (a) mzunguko na (b) eneo.

    Jibu

    314 katika.

    Jibu b

    7850 sq.

    Zoezi\(\PageIndex{20}\):

    Mduara una radius miguu 100. Takriban (a) mzunguko na (b) eneo.

    Jibu

    628 ft.

    Jibu b

    31,400 futi.

    Mfano\(\PageIndex{11}\):

    Mduara una radius sentimita 42.5. Takriban (a) mzunguko na (b) eneo.

    Suluhisho

    (a) Pata mduara wakati r = 42.5.

    Andika formula ya mzunguko. C = 2\(\pi\) r
    badala 3.14 kwa\(\pi\) na 42.5 kwa r. C ≈ 2 (3.14) (42.5)
    Kuzidisha. C ≈ 266.9 sentimita

    (b) Pata eneo wakati r = 42.5.

    Andika formula kwa eneo. A =\(\pi\) r 2
    badala 3.14 kwa\(\pi\) na 42.5 kwa r. A ≈ (3.14) (42.5) 2
    Kuzidisha. A ≈ 5671.625 sentimita za mraba
    Zoezi\(\PageIndex{21}\):

    Mduara una radius sentimita 51.8. Takriban (a) mzunguko na (b) eneo.

    Jibu

    325.304 cm

    Jibu b

    8425.3736 sq sentimita

    Zoezi\(\PageIndex{22}\):

    Mduara una radius mita 26.4. Takriban (a) mzunguko na (b) eneo.

    Jibu

    165.792 m

    Jibu b

    2188.4544 sq. m

    Takriban\(\pi\) na Fraction

    Badilisha sehemu\(\dfrac{22}{7}\) kwa decimal. Ikiwa unatumia calculator yako, nambari ya decimal itajaza maonyesho na kuonyesha 3.14285714. Lakini kama sisi pande zote kwamba idadi ya sehemu mbili decimal, sisi kupata 3.14, makadirio decimal ya\(\pi\). Wakati tuna mduara na Radius kutolewa kama sehemu, tunaweza mbadala\(\dfrac{22}{7}\)\(\pi\) badala ya 3.14. Na,\(\dfrac{22}{7}\) kwa kuwa pia ni makadirio ya π, tutatumia alama ≈ kuonyesha tuna thamani ya takriban.

    Mfano\(\PageIndex{12}\):

    Mduara una\(\dfrac{14}{15}\) mita ya radius. Takriban (a) mzunguko na (b) eneo.

    Suluhisho

    (a) Pata mduara wakati r =\(\dfrac{14}{15}\)

    Andika formula ya mzunguko. C = 2\(\pi\) r
    Mbadala\(\dfrac{22}{7}\) kwa ajili\(\dfrac{14}{15}\) ya\(\pi\) na kwa r. $C\ takriban 2\ kushoto (\ dfrac {22} {7}\ kulia)\ kushoto (\ dfrac {14} {15}\ kulia) $$
    Kuzidisha. C ≈\(\dfrac{88}{15}\) mita

    . (b) Pata eneo wakati r =\(\dfrac{14}{15}\).

    Andika formula kwa eneo. A =\(\pi\) r 2
    Mbadala\(\dfrac{22}{7}\) kwa ajili\(\dfrac{14}{15}\) ya\(\pi\) na kwa r. $A\ takriban\ kushoto (\ dfrac {22} {7}\ kulia)\ kushoto (\ dfrac {14} {15}\ kulia) ^ {2} $$
    Kuzidisha. A ≈ mita\(\dfrac{616}{225}\) za mraba
    Zoezi\(\PageIndex{23}\):

    Mduara una\(\dfrac{5}{21}\) mita za radius. Takriban (a) mzunguko na (b) eneo.

    Jibu

    \(\frac{220}{147}\)m

    Jibu b
    \(\frac{550}{3087}\)sq m
    Zoezi\(\PageIndex{24}\):

    Mduara una\(\dfrac{10}{33}\) inchi za radius. Takriban (a) mzunguko na (b) eneo.

    Jibu

    \(\frac{40}{21}\)katika.

    Jibu b
    \(\frac{200}{693}\)sq. katika.
    PATA RASILIMALI ZA ZIADA

    Kubadilisha Fraction kwa Decimal - Sehemu ya 2

    Badilisha Fraction kwa Decimal (kurudia)

    Linganisha FRACTIONS na Decimals kutumia Ishara za Usawa

    Tambua Eneo la Mzunguko

    Tambua Mzunguko wa Mzunguko

    Mazoezi hufanya kamili

    Geuza FRACTIONS kwa Decimals

    Katika mazoezi yafuatayo, kubadilisha kila sehemu kwa decimal.

    1. \(\dfrac{2}{5}\)
    2. \(\dfrac{4}{5}\)
    3. \(- \dfrac{3}{8}\)
    4. \(- \dfrac{5}{8}\)
    5. \(\dfrac{17}{20}\)
    6. \(\dfrac{13}{20}\)
    7. \(\dfrac{11}{4}\)
    8. \(\dfrac{17}{4}\)
    9. \(- \dfrac{310}{25}\)
    10. \(- \dfrac{284}{25}\)
    11. \(\dfrac{5}{9}\)
    12. \(\dfrac{2}{9}\)
    13. \(\dfrac{15}{11}\)
    14. \(\dfrac{18}{11}\)
    15. \(\dfrac{15}{111}\)
    16. \(\dfrac{25}{111}\)

    Katika mazoezi yafuatayo, kurahisisha maneno.

    1. \(\dfrac{1}{2}\)+ 6.5
    2. \(\dfrac{1}{4}\)+ 10.75
    3. 2.4 +\(\dfrac{5}{8}\)
    4. 3.9 +\(\dfrac{9}{20}\)
    5. 9.73 +\(\dfrac{17}{20}\)
    6. 6.29 +\(\dfrac{21}{40}\)

    Order Decimals na FRACTIONS

    Katika mazoezi yafuatayo, tengeneza kila jozi ya namba, ukitumia < or >.

    1. \(\dfrac{1}{8}\)___0.8
    2. \(\dfrac{1}{4}\)___0.4
    3. \(\dfrac{2}{5}\)___0.25
    4. \(\dfrac{3}{5}\)___0.35
    5. 0.725___\(\dfrac{3}{4}\)
    6. 0.92___\(\dfrac{7}{8}\)
    7. 0.66___\(\dfrac{2}{3}\)
    8. 0.83___\(\dfrac{5}{6}\)
    9. -0.75___\(- \dfrac{4}{5}\)
    10. -0.44___\(- \dfrac{9}{20}\)
    11. \(- \dfrac{3}{4}\)___-0.925
    12. \(- \dfrac{2}{3}\)___-0.632

    Katika mazoezi yafuatayo, weka kila seti ya namba ili kutoka angalau hadi kubwa.

    1. \(\dfrac{3}{5}, \dfrac{9}{16}\), 0.55
    2. \(\dfrac{3}{8}, \dfrac{7}{20}\), 0.36
    3. 0.702,\(\dfrac{13}{20}, \dfrac{5}{8}\)
    4. 0.15,\(\dfrac{3}{16}, \dfrac{1}{5}\)
    5. -0.3,\(- \dfrac{1}{3}, - \dfrac{7}{20}\)
    6. -0.2,\(- \dfrac{3}{20}, - \dfrac{1}{6}\)
    7. \(- \dfrac{3}{4}, - \dfrac{7}{9}\), -0.7
    8. \(- \dfrac{8}{9}, - \dfrac{4}{5}\), -0.9

    Kurahisisha Maneno Kutumia Utaratibu wa Uendeshaji

    Katika mazoezi yafuatayo, kurahisisha.

    1. 10 (25.1 - 43.8)
    2. 30 (18.1 - 32.5)
    3. 62 (9.75 - 4.99)
    4. 42 (8.45 - 5.97)
    5. \(\dfrac{3}{4}\)(12.4 - 4.2)
    6. \(\dfrac{4}{5}\)(8.6 + 3.9)
    7. \(\dfrac{5}{12}\)(30.58 + 17.9)
    8. \(\dfrac{9}{16}\)(21.96 - 9.8)
    9. 10 ÷ 0.1 + (1.8) 4 ÷ (0.3) 2
    10. 5 ÷ 0.5 + (3.9) 6 ÷ (0.7) 2
    11. (37.1 + 52.7) ÷ (12.5 ÷ 62.5)
    12. (11.4 + 16.2) ÷ (18 ÷ 60)
    13. \(\left(\dfrac{1}{5}\right)^{2}\)+ (1.4) (6.5)
    14. \(\left(\dfrac{1}{2}\right)^{2}\)+ (2.1) (8.3)
    15. \(− \dfrac{9}{10} \cdot \dfrac{8}{15}\)+ 0.25
    16. \(− \dfrac{3}{8} \cdot \dfrac{14}{15}\)+ 0.72

    Mazoezi ya mchanganyiko

    Katika mazoezi yafuatayo, kurahisisha. Kutoa jibu kama decimal.

    1. \(3 \dfrac{1}{4}\)- 6.5
    2. \(5 \dfrac{2}{5}\)- 8.75
    3. 10.86 ÷\(\dfrac{2}{3}\)
    4. 5.79 ÷\(\dfrac{3}{4}\)
    5. \(\dfrac{7}{8}\)(103.48) +\(1 \dfrac{1}{2}\) (361)
    6. \(\dfrac{5}{16}\)(117.6) +\(2 \dfrac{1}{3}\) (699)
    7. 3.6\(\left(\dfrac{9}{8} − 2.72\right)\)
    8. 5.1\(\left(\dfrac{12}{5} − 3.91\right)\)

    Pata mzunguko na Eneo la Mizunguko

    Katika mazoezi yafuatayo, takriban (a) mzunguko na (b) eneo la kila mduara. Ikiwa vipimo vinatolewa kwa sehemu ndogo, acha majibu katika fomu ya sehemu.

    1. radius = 5 ndani.
    2. radius = 20 katika.
    3. radius = 9 ft.
    4. radius = 4 ft.
    5. radius = 46 cm
    6. radius = 38 cm
    7. radius = 18.6 m
    8. radius = 57.3 m
    9. radius =\(\dfrac{7}{10}\) maili
    10. radius =\(\dfrac{7}{11}\) maili
    11. radius =\(\dfrac{3}{8}\) yadi
    12. radius =\(\dfrac{5}{12}\) yadi
    13. kipenyo =\(\dfrac{5}{6}\) m
    14. kipenyo =\(\dfrac{3}{4}\) m

    kila siku Math

    1. Kelly anataka kununua jozi ya buti kwamba ni kuuzwa kwa bei\(\dfrac{2}{3}\) ya awali. Bei ya awali ya buti ni $84.99. Je! Bei ya kuuza ya viatu ni nini?
    2. Mbunifu ana mpango wa kuweka mosaic ya mviringo katika kuingia kwa jengo jipya. The mosaic itakuwa katika sura ya mduara na radius ya miguu 6. Ni miguu ngapi ya mraba ya tile itahitajika kwa mosaic? (Pande zote jibu lako hadi idadi nzima ijayo.)

    Mazoezi ya kuandika

    1. Je, ni rahisi kwako kubadili decimal kwa sehemu au sehemu kwa decimal? Eleza.
    2. Eleza hali katika maisha yako ambayo unaweza kuhitaji kupata eneo au mzunguko wa mduara.

    Self Check

    (a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii

    (b) Orodha hii inakuambia nini kuhusu ustadi wako wa sehemu hii? Ni hatua gani utachukua ili kuboresha?

    Wachangiaji na Majina