Skip to main content
Global

4.10: Kuongeza na Ondoa Hesabu Mchanganyiko (Sehemu ya 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    173396

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Mfano wa kuongeza idadi ya mchanganyiko na denominator ya kawaida
    • Ongeza namba zilizochanganywa na denominator ya kawaida
    • Utoaji wa mfano wa namba zilizochanganywa
    • Ondoa idadi mchanganyiko na denominator ya kawaida
    • Kuongeza na Ondoa idadi mchanganyiko na denominators tofauti
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Chora takwimu kwa mfano\(\dfrac{7}{3}\). Ikiwa umekosa tatizo hili, kagua Mfano 4.1.6.
    2. Badilisha\(\dfrac{11}{4}\) kwa idadi iliyochanganywa. Ikiwa umekosa tatizo hili, kagua Mfano 4.1.9.
    3. Badilisha\(3 \dfrac{1}{2}\) kwa sehemu isiyofaa. Kama amekosa tatizo hili, mapitio Mfano 4.1.11.

    Uongezekaji wa Mfano wa Hesabu Mchanganyiko na Denominator ya kawaida

    Hadi sasa, tumeongeza na kuondolewa sehemu sahihi na zisizofaa, lakini sio namba zilizochanganywa. Hebu tuanze kwa kufikiri juu ya kuongeza idadi mchanganyiko kwa kutumia pesa.

    Kama Ron ina\(1\) dola na\(1\) robo, ana\(1 \dfrac{1}{4}\) dola. Kama Don ina\(2\) dola na\(1\) robo, ana\(2 \dfrac{1}{4}\) dola. Nini kama Ron na Don kuweka fedha zao pamoja? Wangeweza kuwa na\(3\) dola na\(2\) robo. Wao kuongeza dola na kuongeza robo. Hii inafanya\(3 \dfrac{2}{4}\) dola. Kwa sababu robo mbili ni dola nusu, wangeweza kuwa\(3\) na dola nusu, au\(3 \dfrac{1}{2}\) dola.

    \[\begin{split} & 1 \dfrac{1}{4} \\ + & 2 \dfrac{1}{4} \\ \hline \\ & 3 \dfrac{2}{4} = 3 \dfrac{1}{2} \end{split} \nonumber \]

    Unapoongeza dola na kisha uongeze robo, ungeongeza namba nzima na kisha uongeze sehemu ndogo.

    \[1 \dfrac{1}{4} + 2 \dfrac{1}{4} \nonumber \]

    Tunaweza kutumia miduara ya sehemu ili kuiga mfano huu:

    Anza na\(1 \dfrac{1}{4}\). \(\dfrac{1}{4}\)vipande moja na moja \(1 \dfrac{1}{4}\)
    Ongeza\(2 \dfrac{1}{4}\) zaidi. wholes mbili na\(\dfrac{1}{4}\) vipande moja 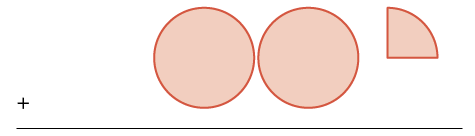\(\begin{split}+ & 2 \dfrac{1}{4} \\ & \hline \end{split}\)
    Jumla ni: wholes tatu na mbili\(\dfrac{1}{4}\) 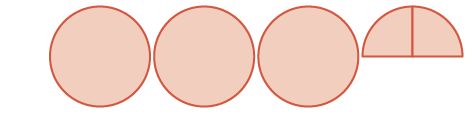\(3 \dfrac{2}{4} = 3 \dfrac{1}{2}\)
    Mfano\(\PageIndex{1}\): model

    Mfano\(2 \dfrac{1}{3} + 1 \dfrac{2}{3}\) na kutoa jumla.

    Suluhisho

    Tutatumia miduara ya sehemu, miduara nzima kwa idadi nzima na\(\dfrac{1}{3}\) vipande kwa sehemu ndogo.

    wholes mbili na moja\(\dfrac{1}{3}\) 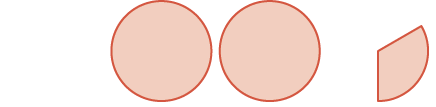\(2 \dfrac{1}{3}\)
    pamoja na moja nzima na mbili\(\dfrac{1}{3}\) s \(\begin{split}+ & 1 \dfrac{2}{3} \\ & \hline \end{split}\)
    jumla ni wholes tatu na tatu\(\dfrac{1}{3}\) s 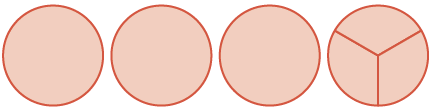\(3 \dfrac{3}{3} = 4\)

    Hii ni sawa na\(4\) wholes. Hivyo,\(2 \dfrac{1}{3} + 1 \dfrac{2}{3} = 4\).

    Zoezi\(\PageIndex{1}\)

    Tumia mfano ili kuongeza zifuatazo. Chora picha ili kuonyesha mfano wako. \(1 \dfrac{2}{5} + 3 \dfrac{3}{5}\)

    Jibu

    \(5\)

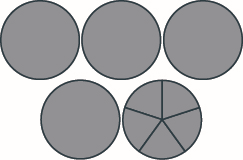
    Ex 4.6.1.png

    Zoezi\(\PageIndex{2}\)

    Tumia mfano ili kuongeza zifuatazo. Chora picha ili kuonyesha mfano wako. \(2 \dfrac{1}{6} + 2 \dfrac{5}{6}\)

    Jibu

    \(5\)

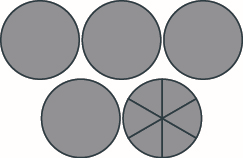
    Ex 4.6.2.png

    Mfano\(\PageIndex{2}\): model

    Mfano\(1 \dfrac{3}{5} + 2 \dfrac{3}{5}\) na kutoa jumla kama idadi mchanganyiko.

    Suluhisho

    Tutatumia miduara ya sehemu, miduara nzima kwa idadi nzima na\(\dfrac{1}{5}\) vipande kwa sehemu ndogo.

    moja nzima na tatu\(\dfrac{1}{5}\) s \(1 \dfrac{3}{5}\)
    pamoja na wholes mbili na tatu\(\dfrac{1}{5}\) s 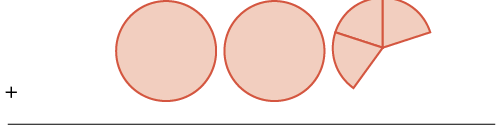\(\begin{split}+ & 2 \dfrac{3}{5} \\ & \hline \end{split}\)
    Jumla ni wholes tatu na sita\(\dfrac{1}{5}\) s 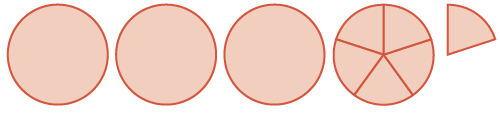\(3 \dfrac{6}{5} = 4 \dfrac{1}{5}\)

    Kuongeza duru nzima na vipande tano, tulipata jumla ya\(3 \dfrac{6}{5}\). Tunaweza kuona kwamba\(\dfrac{6}{5}\) ni sawa na\(1 \dfrac{1}{5}\), hivyo sisi kuongeza kwamba\(3\) kwa kupata\(4 \dfrac{1}{5}\).

    Zoezi\(\PageIndex{3}\)

    Model, na kutoa jumla kama idadi mchanganyiko. Chora picha ili kuonyesha mfano wako. \(2 \dfrac{5}{6} + 1 \dfrac{5}{6}\)

    Jibu

    \(4\dfrac{2}{3}\)

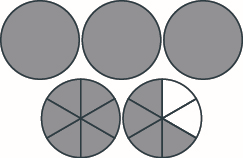
    Ex 4.6.3.png

    Zoezi\(\PageIndex{4}\)

    Model, na kutoa jumla kama idadi mchanganyiko. Chora picha ili kuonyesha mfano wako. \(1 \dfrac{5}{8} + 1 \dfrac{7}{8}\)

    Jibu

    \(3\dfrac{1}{2}\)

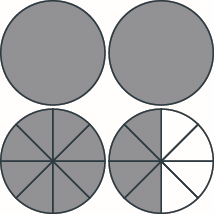
    Ex 4.6.4.png

    Ongeza Hesabu Mchanganyiko

    Mfano na miduara ya sehemu husaidia kuonyesha mchakato wa kuongeza namba zilizochanganywa: Tunaongeza namba nzima na kuongeza sehemu ndogo, na kisha tunapunguza matokeo, ikiwa inawezekana.

    JINSI YA: ONGEZA NAMBA ZILIZOCHANGANYWA NA DENOMINATOR YA KAWAIDA

    Hatua ya 1. Ongeza namba nzima.

    Hatua ya 2. Ongeza sehemu ndogo.

    Hatua ya 3. Kurahisisha, ikiwa inawezekana.

    Mfano\(\PageIndex{3}\): add

    Ongeza:\(3 \dfrac{4}{9} + 2 \dfrac{2}{9}\).

    Suluhisho

    Ongeza namba nzima. \(\begin{split} & \textcolor{red}{3} \dfrac{4}{9} \\ + & \textcolor{red}{2} \dfrac{2}{9} \\ \hline \\ & \textcolor{red}{5} \end{split}\)
    Ongeza sehemu ndogo. \(\begin{split} & 3 \textcolor{red}{\dfrac{4}{9}} \\ + & 2 \textcolor{red}{\dfrac{2}{9}} \\ \hline \\ & 5 \textcolor{red}{\dfrac{6}{9}} \end{split}\)
    Kurahisisha sehemu. \(\begin{split} & 3 \dfrac{4}{9} \\ + & 2 \dfrac{2}{9} \\ \hline \\ & \textcolor{red}{5 \dfrac{6}{9}} = 5 \dfrac{2}{3} \end{split}\)
    Zoezi\(\PageIndex{5}\)

    Pata jumla:\(4 \dfrac{4}{7} + 1 \dfrac{2}{7}\).

    Jibu

    \(5\dfrac{6}{7}\)

    Zoezi\(\PageIndex{6}\)

    Pata jumla:\(2 \dfrac{3}{11} + 5 \dfrac{6}{11}\).

    Jibu

    \(7\dfrac{9}{11}\)

    Katika Mfano\(\PageIndex{3}\), jumla ya sehemu ndogo ilikuwa sehemu sahihi. Sasa tutafanya kazi kupitia mfano ambapo jumla ni sehemu isiyofaa.

    Mfano\(\PageIndex{4}\): add

    Pata jumla:\(9 \dfrac{5}{9} + 5 \dfrac{7}{9}\).

    Suluhisho

    Ongeza namba nzima na kisha uongeze sehemu ndogo. \(\begin{split} & 9 \dfrac{5}{9} \\ + & 5 \dfrac{7}{9} \\ \hline \\ & 14 \dfrac{12}{9} \end{split}\)
    Andika upya\(\dfrac{12}{9}\) kama sehemu isiyofaa. \(14 + 1 \dfrac{3}{9}\)
    Ongeza. \(15 \dfrac{3}{9}\)
    Kurahisisha. \(15 \dfrac{1}{3}\)
    Zoezi\(\PageIndex{7}\)

    Pata jumla:\(8 \dfrac{7}{8} + 7 \dfrac{5}{8}\).

    Jibu

    \(16\dfrac{1}{2}\)

    Zoezi\(\PageIndex{8}\)

    Pata jumla:\(6 \dfrac{7}{9} + 8 \dfrac{5}{9}\).

    Jibu

    \(15\dfrac{1}{3}\)

    Njia mbadala ya kuongeza nambari zilizochanganywa ni kubadili nambari zilizochanganywa kwa sehemu zisizofaa na kisha kuongeza sehemu zisizofaa. Njia hii mara nyingi imeandikwa kwa usawa.

    Mfano\(\PageIndex{5}\): add

    Ongeza kwa kubadili namba zilizochanganywa kwa sehemu zisizofaa:\(3 \dfrac{7}{8} + 4 \dfrac{3}{8}\).

    Suluhisho

    Badilisha kwa sehemu zisizofaa. \(\dfrac{31}{8} + \dfrac{35}{8}\)
    Ongeza sehemu ndogo. \(\dfrac{31 + 35}{8}\)
    Kurahisisha nambari. \(\dfrac{66}{8}\)
    Andika upya kama nambari iliyochanganywa. \(8 \dfrac{2}{8}\)
    Kurahisisha sehemu. \(8 \dfrac{1}{4}\)

    Tangu tatizo lilipewa kwa fomu ya nambari iliyochanganywa, tutaandika jumla kama namba iliyochanganywa.

    Zoezi\(\PageIndex{9}\)

    Pata jumla kwa kubadili namba zilizochanganywa kwa sehemu zisizofaa:\(5 \dfrac{5}{9} + 3 \dfrac{7}{9}\)

    Jibu

    \(9\dfrac{1}{3}\)

    Zoezi\(\PageIndex{10}\)

    Pata jumla kwa kubadili namba zilizochanganywa kwa sehemu zisizofaa:\(3 \dfrac{7}{10} + 2 \dfrac{9}{10}\)

    Jibu

    \(6\dfrac{3}{5}\)

    Jedwali\(\PageIndex{1}\) linalinganisha njia mbili za kuongeza, kwa kutumia maneno\(3 \dfrac{2}{5} + 6 \dfrac{4}{5}\) kama mfano. Unapendelea njia ipi?

    Jedwali\(\PageIndex{1}\)
    Mchanganyiko Hesabu Vipande visivyofaa
    \(\begin{split} & 3 \dfrac{2}{5} \\ + & 6 \dfrac{4}{5} \\ \hline \\ & 9 \dfrac{6}{5} \end{split}\) \(3 \dfrac{2}{5} + 6 \dfrac{4}{5}\)
    \(9 + \dfrac{6}{5}\) \(\dfrac{17}{5} + \dfrac{34}{5}\)
    \(9 + 1 \dfrac{1}{5}\) \(\dfrac{51}{5}\)
    \(10 \dfrac{1}{5}\) \(10 \dfrac{1}{5}\)

    Utoaji wa mfano wa Hesabu Mchanganyiko

    Hebu fikiria pizzas tena ili kutoa mfano wa idadi ya mchanganyiko na denominator ya kawaida. Tuseme umeoka pizza nzima na unataka kumpa ndugu yako nusu ya pizza. Unapaswa kufanya nini kwa pizza kumpa nusu? Una kukata ndani ya vipande viwili. Kisha unaweza kumpa nusu.

    Tutatumia miduara ya sehemu (pizzas!) ili kutusaidia taswira ya mchakato. Anza kwa moja nzima.

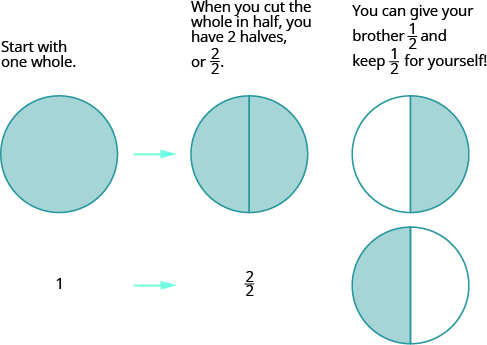
    Mduara wa kivuli unaonyeshwa. Chini ni 1. Kuna mishale inayoelekeza mduara wa kivuli umegawanyika katika sehemu mbili sawa. Chini ni 2 juu ya 2. Karibu na hii ni miduara miwili, kila mmoja imegawanywa katika sehemu mbili sawa. Mduara wa juu una nusu ya haki ya kivuli na mduara wa chini una nusu ya kushoto yenye kivuli.

    Kielelezo\(\PageIndex{1}\)

    Algebraically, ungependa kuandika:

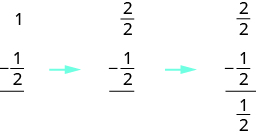
    Kwenye upande wa kushoto, inasema 1 chini ya nusu 1. Kuna mshale unaoelezea 2 juu ya 2 chini ya 1 juu ya 2. Kuna mshale mwingine akizungumzia 2 juu ya 2 bala 1 juu ya 2 sawa 1 juu ya 2.

    Mfano\(\PageIndex{6}\): subtract

    Tumia mfano wa kuondoa:\(1 − \dfrac{1}{3}\).

    Suluhisho

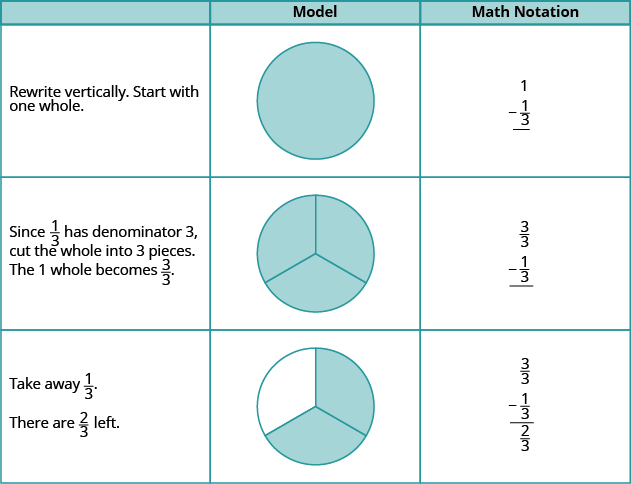
    Kuna meza yenye safu tano na nguzo tatu. Safu ya kwanza haijaandikwa. Safu ya pili inaitwa “Mfano.” Safu ya tatu inaitwa “Math Notation.” Katika safu ya kwanza, mstari wa kwanza unasema, “Andika upya kwa wima. Anza kwa moja nzima.” Mstari unaofuata unasema, “Kwa kuwa theluthi moja ina denominator 3, kata nzima vipande 3. 1 nzima inakuwa 3 theluthi.” Mstari uliofuata unasema, “Ondoa theluthi moja.” Mstari wa mwisho unasema, “Kuna theluthi mbili zilizobaki.” Katika safu ya “Mfano”, kuna picha ya mduara wa kivuli. Chini hiyo ni picha ya mduara uliovuliwa umegawanywa katika vipande vitatu sawa. Chini hiyo ni picha ya mduara iliyogawanywa katika vipande 3 sawa na vipande viwili vilivyovuliwa. Katika safu ya “Math Notation”, mstari wa kwanza unaonyesha 1 chini ya tatu. Mstari unaofuata unasema theluthi 3 chini ya tatu. Mstari wa mwisho unasema theluthi 3 chini ya 1 ya tatu ni theluthi 2.

    Zoezi\(\PageIndex{11}\)

    Tumia mfano wa kuondoa:\(1 − \dfrac{1}{4}\).

    Jibu

    \(\dfrac{3}{4}\)

    Zoezi\(\PageIndex{12}\)

    Tumia mfano wa kuondoa:\(1 − \dfrac{1}{5}\).

    Jibu

    \(\dfrac{4}{5}\)

    Nini kama sisi kuanza na zaidi ya moja nzima? Hebu tujue.

    Mfano\(\PageIndex{7}\): subtract

    Tumia mfano wa kuondoa:\(2 − \dfrac{3}{4}\).

    Suluhisho

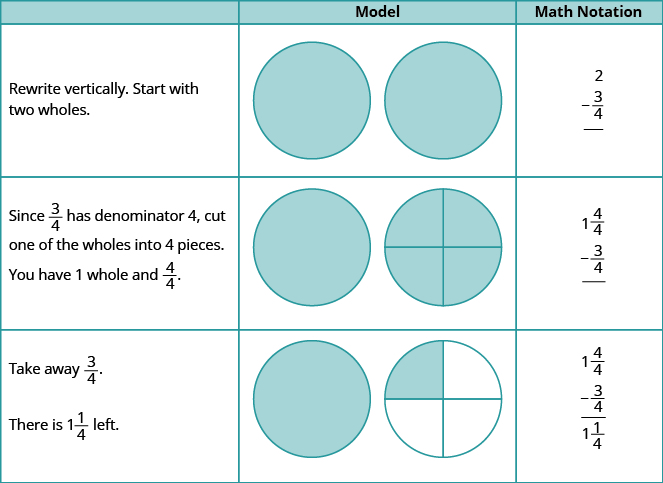
    Kuna meza yenye safu nne na nguzo tatu. Safu ya kwanza haijaandikwa. Safu ya pili inaitwa “Mfano.” Safu ya tatu inaitwa “Math Notation.” Katika safu ya kwanza, mstari wa kwanza unasema, “Andika upya kwa wima. Anza kwa wholes mbili. Mstari unaofuata unasema, “Tangu tatu nne zina denominator 4, kata moja ya vipande vipande 4. Una moja nzima na nne nne.” Mstari uliofuata unasema, “Ondoa nne tatu.” Mstari wa mwisho unasema, “Kuna 1 na 1 kushoto ya nne.” Katika safu ya “Mfano”, kuna picha ya miduara miwili ya kivuli. Chini hiyo ni picha ya duru mbili za kivuli. Moja ya miduara imegawanywa katika vipande 4 sawa. Chini hiyo ni picha ya mduara mmoja kamili wa kivuli na mduara umegawanyika katika vipande 4 sawa na kipande 1 kivuli. Katika safu ya “Math Notation”, mstari wa kwanza unaonyesha 2 minus 3 ya nne. Mstari unaofuata unasema 1 na 4 nne minus 3 nne. Mstari wa mwisho unasema 1 na 4 nne minus 3 nne sawa na 1 na 1 ya nne.

    Zoezi\(\PageIndex{13}\)

    Tumia mfano wa kuondoa:\(2 − \dfrac{1}{5}\).

    Jibu

    \(\dfrac{9}{5}\)

    Zoezi\(\PageIndex{14}\)

    Tumia mfano wa kuondoa:\(2 − \dfrac{1}{3}\).

    Jibu

    \(\dfrac{5}{3}\)

    Katika mfano unaofuata, tutaondoa zaidi ya moja nzima.

    Mfano\(\PageIndex{8}\): subtract

    Tumia mfano wa kuondoa:\(2 − 1 \dfrac{2}{5}\).

    Suluhisho

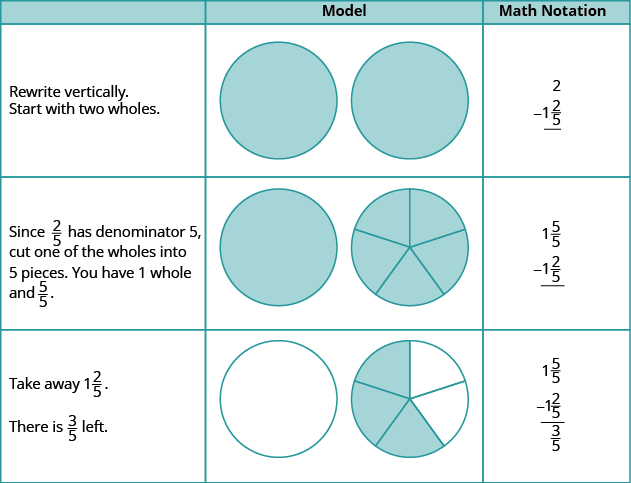
    Kuna meza yenye safu tano na nguzo tatu. Safu ya kwanza haijaandikwa. Safu ya pili inaitwa “Mfano.” Safu ya tatu inaitwa “Math Notation.” Katika safu ya kwanza, mstari wa kwanza unasema, “Andika upya kwa wima. Anza kwa wholes mbili. Mstari unaofuata unasema, “Kwa kuwa mbili-tano ina denominator 5, kata moja ya vipande vipande 5. Una moja nzima na tano tano.” Mstari unaofuata unasema, “Ondoa 1 na mbili-tano.” Mstari wa mwisho unasema, “Kuna 3 tano kushoto.” Katika safu ya “Mfano”, kuna picha ya miduara miwili ya kivuli. Chini hiyo ni picha ya duru mbili za kivuli. Moja ya miduara imegawanywa katika vipande 5 sawa. Chini hiyo ni picha ya mduara mmoja usio na shaded na mduara umegawanywa katika vipande 5 sawa na vipande 3 vilivyovuliwa. Katika safu ya “Math Notation”, mstari wa kwanza unaonyesha 2 minus 1 na 2 tano. Mstari unaofuata unasema 1 na 5 tano chini ya 1 na 2 tano. Mstari wa mwisho unasema 1 na 5 tano minus 1 na 2 tano sawa na 3 tano.

    Zoezi\(\PageIndex{15}\)

    Tumia mfano wa kuondoa:\(2 − 1 \dfrac{1}{3}\).

    Jibu

    \(\dfrac{2}{3}\)

    Zoezi\(\PageIndex{16}\)

    Tumia mfano wa kuondoa:\(2 − 1 \dfrac{1}{4}\).

    Jibu

    \(\dfrac{3}{4}\)

    Nini kama unapoanza na nambari iliyochanganywa na unahitaji kuondoa sehemu? Fikiria juu ya hali hii: Unahitaji kuweka robo tatu katika mita ya maegesho, lakini una\(\$1\) muswada tu na robo moja. Unaweza kufanya nini? Unaweza kubadilisha muswada wa dola katika\(4\) robo. Thamani ya\(4\) robo ni sawa na muswada wa dola moja, lakini\(4\) robo ni muhimu zaidi kwa mita ya maegesho. Sasa, badala ya kuwa na\(\$1\) muswada na robo moja, una\(5\) robo na unaweza kuweka\(3\) robo katika mita.

    Mifano hii kinachotokea wakati tunapoondoa sehemu kutoka kwa nambari iliyochanganywa. Sisi subtracted robo tatu kutoka dola moja na robo moja.

    Tunaweza pia mfano huu kwa kutumia duru sehemu, kiasi kama tulivyofanya kwa kuongeza idadi mchanganyiko.

    Mfano\(\PageIndex{9}\): subtract

    Tumia mfano wa kuondoa:\(1 \dfrac{1}{4} − \dfrac{3}{4}\)

    Suluhisho

    Andika upya kwa wima. Anza na moja nzima na moja ya nne. 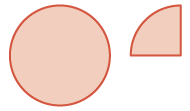\(\begin{split} & \textcolor{red}{1 \dfrac{1}{4}} \\ - & \dfrac{3}{4} \\ \hline \end{split}\)
    Kwa kuwa sehemu ndogo zina denominator 4, kata nzima vipande 4. Sasa una\(\dfrac{4}{4}\) na\(\dfrac{1}{4}\) ambayo ni\(\dfrac{5}{4}\). 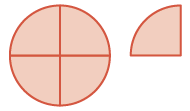\(\begin{split} & \textcolor{red}{\dfrac{5}{4}} \\ - & \dfrac{3}{4} \\ \hline \end{split}\)
    Chukua mbali\(\dfrac{3}{4}\). Kuna\(\dfrac{1}{2}\) kushoto. 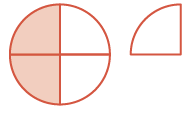\(\begin{split} & \dfrac{5}{4}\\\textcolor{red}{- & \dfrac}3}{4}}\\ \hline \\ & \dfrac{2}{4} = \dfrac{1}{2} \end{split}\)
    Zoezi\(\PageIndex{17}\)

    Tumia mfano wa kuondoa. Chora picha ili kuonyesha mfano wako. \(1 \dfrac{1}{3} − \dfrac{2}{3}\)

    Jibu

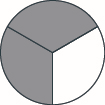
    Ex 4.6.17.png

    Zoezi\(\PageIndex{18}\)

    Tumia mfano wa kuondoa. Chora picha ili kuonyesha mfano wako. \(1 \dfrac{1}{5} − \dfrac{4}{5}\)

    Jibu

    Ex 4.6.18.png

    Wachangiaji na Attributi