Skip to main content
Global

4.3: Kuzidisha na Gawanya sehemu ndogo (Sehemu ya 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    173386

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Kurahisisha sehemu
    • Kuzidisha vipande
    • Kupata kurudisha
    • Gawanya vipande
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kupata factorization mkuu wa\(48\). Ikiwa umekosa tatizo hili, kagua Mfano 2.5.1.
    2. Chora mfano wa sehemu\(\dfrac{3}{4}\). Ikiwa umekosa tatizo hili, tathmini Mfano 4.1.2.
    3. Kupata sehemu mbili sawa na\(\dfrac{5}{6}\). Majibu yanaweza kutofautiana. Majibu ya kukubalika ni pamoja na\(\dfrac{10}{12}, \dfrac{15}{18}, \dfrac{50}{60}\), nk Kama amekosa tatizo hili, mapitio Mfano 4.1.14.

    Kurahisisha Fractions

    Katika kufanya kazi na sehemu ndogo sawa, umeona kwamba kuna njia nyingi za kuandika sehemu ndogo ambazo zina thamani sawa, au zinawakilisha sehemu sawa ya yote. Unajuaje ni nani atakayeitumia? Mara nyingi, tutatumia sehemu iliyo katika fomu rahisi.

    Sehemu inachukuliwa kuwa rahisi ikiwa hakuna mambo ya kawaida, isipokuwa\(1\), katika nambari na denominator. Ikiwa sehemu ina mambo ya kawaida katika nambari na denominator, tunaweza kupunguza sehemu kwa fomu yake rahisi kwa kuondoa mambo ya kawaida.

    Ufafanuzi: Sehemu rahisi

    Sehemu inachukuliwa kuwa rahisi ikiwa hakuna mambo ya kawaida katika nambari na denominator.

    Kwa mfano,

    • \(\dfrac{2}{3}\)ni rahisi kwa sababu hakuna sababu ya kawaida ya\(2\) na\(3\).
    • \(\dfrac{10}{15}\)si rahisi kwa sababu\(5\) ni sababu ya kawaida ya\(10\) na\(15\).

    Mchakato wa kurahisisha sehemu mara nyingi huitwa kupunguza sehemu. Katika sehemu iliyotangulia, tulitumia Mali ya Fractions sawa ili kupata sehemu ndogo sawa. Tunaweza pia kutumia sawa FRACTIONS Mali katika reverse ili kurahisisha sehemu. Tunaandika tena mali ili kuonyesha fomu zote mbili pamoja.

    Ufafanuzi: Sawa Fractions Mali

    Ikiwa\(a, b, c\) ni namba wapi\(b ≠ 0, c ≠ 0\), basi\(\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c}\) na\(\dfrac{a \cdot c}{b \cdot c} = \dfrac{a}{b}\).

    Angalia kwamba\(c\) ni jambo la kawaida katika nambari na denominator. Wakati wowote tuna sababu ya kawaida katika nambari na denominator, inaweza kuondolewa.

    JINSI YA: KURAHISISHA SEHEMU

    Hatua ya 1. Andika upya nambari na denominator ili kuonyesha mambo ya kawaida. Ikiwa inahitajika, fikiria namba na denominator katika idadi kubwa.

    Hatua ya 2. Kurahisisha, kwa kutumia sehemu sawa mali, kwa kuondoa mambo ya kawaida.

    Hatua ya 3. Panua mambo yoyote iliyobaki.

    Mfano\(\PageIndex{1}\): simplify

    Kurahisisha:\(\dfrac{10}{15}\).

    Suluhisho

    Ili kurahisisha sehemu, tunatafuta mambo yoyote ya kawaida katika namba na denominator.

    Kumbuka kwamba 5 ni sababu ya wote 10 na 15. \(\dfrac{10}{15}\)
    Fanya namba na denominator. \(\dfrac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}}\)
    Ondoa mambo ya kawaida. \(\dfrac{2 \cdot \cancel{\textcolor{red}{5}}}{3 \cdot \cancel{\textcolor{red}{5}}}\)
    Kurahisisha. \(\dfrac{2}{3}\)
    Zoezi\(\PageIndex{1}\)

    Kurahisisha:\(\dfrac{8}{12}\).

    Jibu

    \(\dfrac{2}{3}\)

    Zoezi\(\PageIndex{2}\)

    Kurahisisha:\(\dfrac{12}{16}\).

    Jibu

    \(\dfrac{3}{4}\)

    Ili kurahisisha sehemu hasi, tunatumia mchakato huo kama katika Mfano\(\PageIndex{1}\). Kumbuka kuweka ishara hasi.

    Mfano\(\PageIndex{2}\): simplify

    Kurahisisha:\(− \dfrac{18}{24}\).

    Suluhisho

    Tunaona kwamba 18 na 24 zote mbili zina sababu za 6. \(- \dfrac{18}{24}\)
    Andika upya nambari na denominator kuonyesha sababu ya kawaida. \(- \dfrac{3 \cdot \textcolor{red}{6}}{4 \cdot \textcolor{red}{6}}\)
    Ondoa mambo ya kawaida. \(- \dfrac{3 \cdot \cancel{\textcolor{red}{6}}}{4 \cdot \cancel{\textcolor{red}{6}}}\)
    Kurahisisha. \(- \dfrac{3}{4}\)
    Zoezi\(\PageIndex{3}\)

    Kurahisisha:\(− \dfrac{21}{28}\).

    Jibu

    \(-\dfrac{3}{4}\)

    Zoezi\(\PageIndex{4}\)

    Kurahisisha:\(− \dfrac{16}{24}\).

    Jibu

    \(-\dfrac{2}{3}\)

    Baada ya kurahisisha sehemu, daima ni muhimu kuangalia matokeo ili kuhakikisha kwamba nambari na denominator hazina mambo mengine sawa. Kumbuka, ufafanuzi wa sehemu rahisi: sehemu inachukuliwa kuwa rahisi ikiwa hakuna sababu za kawaida katika namba na denominator.

    Tunapopunguza sehemu isiyofaa, hakuna haja ya kuibadilisha kwa nambari iliyochanganywa.

    Mfano\(\PageIndex{3}\):

    Kurahisisha:\(− \dfrac{56}{32}\).

    Suluhisho

      \(- \dfrac{56}{32}\)
    Andika upya namba na denominator, kuonyesha mambo ya kawaida, 8. \(- \dfrac{7 \cdot \textcolor{red}{8}}{4 \cdot \textcolor{red}{8}}\)
    Ondoa mambo ya kawaida. \(- \dfrac{7 \cdot \cancel{\textcolor{red}{8}}}{4 \cdot \cancel{\textcolor{red}{8}}}\)
    Kurahisisha. \(- \dfrac{7}{4}\)
    Zoezi\(\PageIndex{5}\)

    Kurahisisha:\(− \dfrac{54}{42}\).

    Jibu

    \(-\dfrac{9}{7}\)

    Zoezi\(\PageIndex{6}\)

    Kurahisisha:\(− \dfrac{81}{45}\).

    Jibu

    \(-\dfrac{9}{5}\)

    JINSI YA: KURAHISISHA SEHEMU

    Hatua ya 1. Andika upya nambari na denominator ili kuonyesha mambo ya kawaida. Ikiwa inahitajika, fikiria namba na denominator katika idadi kubwa.

    Hatua ya 2. Kurahisisha, kwa kutumia sehemu sawa mali, kwa kuondoa mambo ya kawaida.

    Hatua ya 3. Panua mambo yoyote iliyobaki.

    Wakati mwingine inaweza kuwa si rahisi kupata mambo ya kawaida ya nambari na denominator. Wazo nzuri, basi, ni kuzingatia nambari na denominator katika idadi kubwa. (Unaweza kutaka kutumia njia ya mti wa sababu kutambua sababu kuu.) Kisha ugawanye mambo ya kawaida kwa kutumia Mali sawa ya FRACTIONS.

    Mfano\(\PageIndex{4}\): simplify

    Kurahisisha:\(\dfrac{210}{385}\).

    Suluhisho

      \(\dfrac{210}{385}\)
    Tumia miti ya sababu ili kuzingatia nambari na denominator.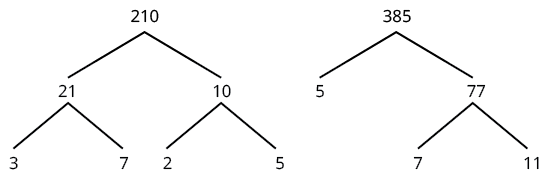
    Andika upya nambari na denominator kama bidhaa ya primes. \(\dfrac{210}{385} = \dfrac{2 \cdot 3 \cdot 5 \cdot 7}{5 \cdot 7 \cdot 11}\)
    Ondoa mambo ya kawaida. \(\dfrac{2 \cdot 3 \cdot \cancel{\textcolor{blue}{5}} \cdot \cancel{\textcolor{red}{7}}}{\cancel{\textcolor{blue}{5}} \cdot \cancel{\textcolor{red}{7}} \cdot 11}\)
    Kurahisisha. \(\dfrac{2 \cdot 3}{11}\)
    Panua mambo yoyote iliyobaki. \(\dfrac{6}{11}\)
    Zoezi\(\PageIndex{7}\)

    Kurahisisha:\(\dfrac{69}{120}\).

    Jibu

    \(\dfrac{23}{40}\)

    Zoezi\(\PageIndex{8}\)

    Kurahisisha:\(\dfrac{120}{192}\).

    Jibu

    \(\dfrac{5}{8}\)

    Tunaweza pia kurahisisha sehemu zenye vigezo. Ikiwa variable ni sababu ya kawaida katika nambari na denominator, tunaiondoa kama tunavyofanya na sababu integer.

    Mfano\(\PageIndex{5}\): simplify

    Kurahisisha:\(\dfrac{5xy}{15x}\).

    Suluhisho

      \(\dfrac{5xy}{15x}\)
    Andika upya nambari na denominator kuonyesha mambo ya kawaida. \(\dfrac{5 \cdot x \cdot y}{3 \cdot 5 \cdot x}\)
    Ondoa mambo ya kawaida. \(\dfrac{\cancel{5} \cdot \cancel{x} \cdot y}{3 \cdot \cancel{5} \cdot \cancel{x}}\)
    Kurahisisha. \(\dfrac{y}{3}\)
    Zoezi\(\PageIndex{9}\)

    Kurahisisha:\(\dfrac{7x}{7y}\).

    Jibu

    \(\dfrac{x}{y}\)

    Zoezi\(\PageIndex{10}\)

    Kurahisisha:\(\dfrac{9a}{9b}\).

    Jibu

    \(\dfrac{a}{b}\)

    Kuzidisha vipande

    Mfano unaweza kukusaidia kuelewa kuzidisha kwa sehemu ndogo. Tutatumia tiles za sehemu kwa mfano\(\dfrac{1}{2} \cdot \dfrac{3}{4}\). Ili kuzidisha\(\dfrac{1}{2}\) na\(\dfrac{3}{4}\),\(\dfrac{1}{2}\) fikiria\(\dfrac{3}{4}\).

    Anza na matofali ya sehemu kwa nne tatu. Ili kupata nusu ya nne tatu, tunahitaji kugawanya katika makundi mawili sawa. Kwa kuwa hatuwezi kugawanya\(\dfrac{1}{4}\) tiles tatu sawasawa katika sehemu mbili, sisi kubadilishana yao kwa tiles ndogo.

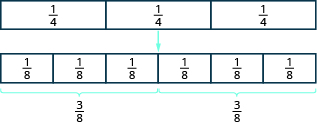
    Mstatili umegawanywa kwa wima katika vipande vitatu sawa. Kila kipande kinachoitwa kama moja ya nne. Kuna mshale unaoelezea mstatili unaofanana umegawanyika kwa wima katika vipande sita sawa. Kila kipande kinachoitwa kama moja ya nane. Kuna braces kuonyesha kwamba tatu ya rectangles hizi kuwakilisha tatu nane.

    Kielelezo\(\PageIndex{1}\)

    Tunaona\(\dfrac{6}{8}\) ni sawa na\(\dfrac{3}{4}\). Kuchukua nusu ya\(\dfrac{1}{8}\) tiles sita inatupa\(\dfrac{1}{8}\) tiles tatu, yaani\(\dfrac{3}{8}\). Kwa hiyo,

    \[\dfrac{1}{2} \cdot \dfrac{3}{4} = \dfrac{3}{8} \nonumber \]

    Mfano\(\PageIndex{6}\): model a fraction

    Tumia mchoro wa mfano\(\dfrac{1}{2} \cdot \dfrac{3}{4}\).

    Suluhisho

    Kivuli cha kwanza katika\(\dfrac{3}{4}\) mstatili.

    Mstatili unaonyeshwa, umegawanyika kwa wima katika vipande vinne sawa. Vipande vitatu ni kivuli.

    Tutachukua hii\(\dfrac{3}{4}\),\(\dfrac{1}{2}\) kwa hiyo sisi kivuli kikubwa\(\dfrac{1}{2}\) cha eneo la kivuli.

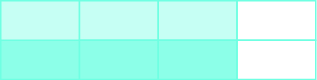
    Mstatili unaonyeshwa, umegawanyika kwa wima katika vipande vinne sawa. Vipande vitatu ni kivuli. Mstatili umegawanywa na mstari usio na usawa, na kujenga vipande nane sawa. Tatu kati ya vipande nane ni kivuli giza.

    Kumbuka kwamba 3 kati ya 8 vipande ni kivuli sana. Hii ina maana kwamba\(\dfrac{3}{8}\) ya mstatili ni kivuli sana. Kwa hiyo,\(\dfrac{1}{2}\) ya\(\dfrac{3}{4}\) ni\(\dfrac{3}{4}\), au\(\dfrac{1}{2} \cdot \dfrac{3}{4} = \dfrac{3}{8}\).

    Zoezi\(\PageIndex{11}\)

    Tumia mchoro wa mfano:\(\dfrac{1}{2} \cdot \dfrac{3}{5}\).

    Jibu

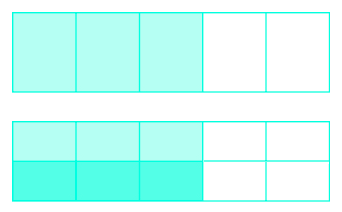
    Mstatili unaonyeshwa, umegawanywa kwa wima katika vipande vitano sawa. Vipande vitatu ni kivuli. Mstatili umegawanywa na mstari usio na usawa, na kujenga vipande kumi sawa. Tatu kati ya vipande kumi ni kivuli giza.

    \(\dfrac{3}{10}\)

    Zoezi\(\PageIndex{12}\)

    Tumia mchoro wa mfano:\(\dfrac{1}{2} \cdot \dfrac{5}{6}\).

    Jibu

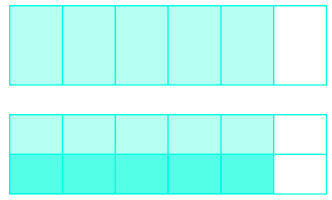
    Mstatili unaonyeshwa, umegawanyika kwa wima katika vipande sita sawa. Tano ya vipande ni kivuli. Mstatili umegawanywa na mstari usio na usawa, na kujenga maeneo kumi na mawili sawa. Tano kati ya vipande kumi na mbili ni kivuli giza.

    \(\dfrac{5}{12}\)

    Angalia matokeo tuliyopata kutoka kwa mfano katika Mfano\(\PageIndex{6}\). Tuligundua kwamba\(\dfrac{1}{2} \cdot \dfrac{3}{4} = \dfrac{3}{8}\). Je, unatambua kwamba tunaweza kupata jibu sawa kwa kuzidisha nambari na kuzidisha denominators?

      \(\dfrac{1}{2} \cdot \dfrac{3}{4}\)
    Kuzidisha nambari, na kuzidisha denominators. \(\dfrac{1}{2} \cdot \dfrac{3}{4}\)
    Kurahisisha. \(\dfrac{3}{8}\)

    Hii inasababisha ufafanuzi wa kuzidisha sehemu. Ili kuzidisha sehemu ndogo, tunazidisha nambari na kuzidisha denominators. Kisha tunaandika sehemu katika fomu rahisi.

    Ufafanuzi: Kuzidisha sehemu

    Ikiwa\(a, b, c,\) na\(d\) ni namba wapi\(b ≠ 0\) na\(d ≠ 0\), basi

    \[\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\]

    Mfano\(\PageIndex{7}\): multiply

    Panua, na uandike jibu kwa fomu rahisi:\(\dfrac{3}{4} \cdot \dfrac{1}{5}\).

    Suluhisho

      \(\dfrac{3}{4} \cdot \dfrac{1}{5}\)
    Kuzidisha nambari, na kuzidisha denominators. \(\dfrac{3 \cdot 1}{4 \cdot 5}\)
    Kurahisisha. \(\dfrac{3}{20}\)

    Hakuna mambo ya kawaida, hivyo sehemu ni rahisi.

    Zoezi\(\PageIndex{13}\)

    Panua, na uandike jibu kwa fomu rahisi:\(\dfrac{1}{3} \cdot \dfrac{2}{5}\).

    Jibu

    \(\dfrac{2}{15}\)

    Zoezi\(\PageIndex{14}\)

    Panua, na uandike jibu kwa fomu rahisi:\(\dfrac{3}{5} \cdot \dfrac{7}{8}\).

    Jibu

    \(\dfrac{21}{40}\)

    Wakati wa kuzidisha sehemu ndogo, mali ya nambari nzuri na hasi bado hutumika. Ni wazo nzuri kuamua ishara ya bidhaa kama hatua ya kwanza. Katika Mfano\(\PageIndex{8}\) tutazidisha hasi mbili, hivyo bidhaa itakuwa chanya.

    Mfano\(\PageIndex{8}\): multiply

    Panua, na uandike jibu kwa fomu rahisi:\(- \dfrac{5}{8} \left(- \dfrac{2}{3}\right)\).

    Suluhisho

      \(- \dfrac{5}{8} \left(- \dfrac{2}{3}\right)\)
    Ishara ni sawa, hivyo bidhaa ni chanya. Kuzidisha nambari, kuzidisha denominators. \(\dfrac{5 \cdot 2}{8 \cdot 3}\)
    Kurahisisha. \(\dfrac{10}{24}\)
    Angalia mambo ya kawaida katika nambari na denominator. Andika upya kuonyesha mambo ya kawaida. \(\dfrac{5 \cdot \cancel{\textcolor{red}{2}}}{12 \cdot \cancel{\textcolor{red}{2}}}\)
    Ondoa mambo ya kawaida. \(\dfrac{5}{12}\)

    Njia nyingine ya kupata bidhaa hii inahusisha kuondoa mambo ya kawaida mapema.

      \(- \dfrac{5}{8} \left(- \dfrac{2}{3}\right)\)
    Tambua ishara ya bidhaa. Kuzidisha. \(\dfrac{5 \cdot 2}{8 \cdot 3}\)
    Onyesha mambo ya kawaida na kisha uwaondoe. \(\dfrac{5 \cdot \cancel{\textcolor{red}{2}}}{12 \cdot \cancel{\textcolor{red}{2}}}\)
    Kuzidisha mambo yaliyobaki. \(\dfrac{5}{12}\)

    Tunapata matokeo sawa.

    Zoezi\(\PageIndex{15}\)

    Panua, na uandike jibu kwa fomu rahisi:\(- \dfrac{4}{7} \left(- \dfrac{5}{8}\right)\).

    Jibu

    \(\dfrac{5}{14}\)

    Zoezi\(\PageIndex{16}\)

    Panua, na uandike jibu kwa fomu rahisi:\(- \dfrac{7}{12} \left(- \dfrac{8}{9}\right)\).

    Jibu

    \(\dfrac{14}{27}\)

    Mfano\(\PageIndex{9}\): multiply

    Panua, na uandike jibu kwa fomu rahisi:\(− \dfrac{14}{15} \cdot \dfrac{20}{21}\).

    Suluhisho

      \(- \dfrac{14}{15} \cdot \dfrac{20}{21}\)
    Kuamua ishara ya bidhaa; kuzidisha. \(- \dfrac{14}{15} \cdot \dfrac{20}{21}\)
    Je, kuna mambo yoyote ya kawaida katika nambari na denominator? Tunajua kwamba 7 ni sababu ya 14 na 21, na 5 ni sababu ya 20 na 15.  
    Andika upya kuonyesha mambo ya kawaida. \(- \dfrac{2 \cdot \cancel{\textcolor{red}{7}} \cdot 4 \cdot \cancel{\textcolor{red}{5}}}{3 \cdot \cancel{\textcolor{red}{5}} \cdot 3 \cdot \cancel{\textcolor{red}{7}}}\)
    Ondoa mambo ya kawaida. \(- \dfrac{2 \cdot 4}{3 \cdot 3}\)
    Panua mambo yaliyobaki. \(- \dfrac{8}{9}\)
    Zoezi\(\PageIndex{17}\)

    Panua, na uandike jibu kwa fomu rahisi:\(− \dfrac{10}{28} \cdot \dfrac{8}{15}\).

    Jibu

    \(-\dfrac{4}{21}\)

    Zoezi\(\PageIndex{18}\)

    Panua, na uandike jibu kwa fomu rahisi:\(− \dfrac{9}{20} \cdot \dfrac{5}{12}\).

    Jibu

    \(-\dfrac{3}{16}\)

    Wakati wa kuzidisha sehemu kwa integer, inaweza kuwa na manufaa kuandika integer kama sehemu. integer yoyote, a, inaweza kuandikwa kama\(\dfrac{a}{1}\). Kwa hiyo\(3 = \dfrac{3}{1}\), kwa mfano.

    Mfano\(\PageIndex{10}\):

    Panua, na uandike jibu kwa fomu rahisi:

    1. \(\dfrac{1}{7} \cdot 56\)
    2. \(\dfrac{12}{5} (−20x)\)

    Suluhisho

      \(\dfrac{1}{7} \cdot 56\)
    Andika 56 kama sehemu. \(\dfrac{1}{7} \cdot \dfrac{56}{1}\)
    Kuamua ishara ya bidhaa; kuzidisha. \(\dfrac{56}{7}\)
    Kurahisisha. \(8\)
      \(\dfrac{12}{5} (-20x)\)
    Andika -20x kama sehemu. \(\dfrac{12}{5} \left(\dfrac{-20x}{1}\right)\)
    Kuamua ishara ya bidhaa; kuzidisha. \(- \dfrac{12 \cdot 20 \cdot x}{5 \cdot 1}\)
    Onyesha mambo ya kawaida na kisha uwaondoe. \(- \dfrac{12 \cdot \textcolor{red}{4 \cdot \cancel{5} x}}{\cancel{5} \cdot 1}\)
    Kuzidisha mambo yaliyobaki; kurahisisha. \(-48x\)
    Zoezi\(\PageIndex{19}\)

    Panua, na uandike jibu kwa fomu rahisi:

    1. \(\dfrac{1}{8} • 72\)
    2. \(\dfrac{11}{3} (−9a)\)
    Jibu

    \(9\)

    Jibu b

    \(-33a\)

    Zoezi\(\PageIndex{20}\)

    Panua, na uandike jibu kwa fomu rahisi:

    1. \(\dfrac{3}{8} • 64\)
    2. \(16x • \dfrac{11}{12}\)
    Jibu

    \(24\)

    Jibu b

    \(\dfrac{44x}{3}\)

    Wachangiaji na Majina