Skip to main content
Global

4.2: Tazama sehemu ndogo (Sehemu ya 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    173404

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Mfano sawa Fractions

    Hebu fikiria kuhusu Andy na Bobby na chakula chao favorite tena. Kama Andy anakula\(\dfrac{1}{2}\) ya pizza na Bobby anakula\(\dfrac{2}{4}\) ya pizza, je, wao kuliwa kiasi hicho cha pizza? Kwa maneno mengine, je,\(\dfrac{1}{2} = \dfrac{2}{4}\)? Tunaweza kutumia vigae sehemu ya kujua kama Andy na Bobby wamekula sehemu sawa ya pizza.

    Ufafanuzi: Sehemu sawa

    Sehemu ndogo sawa ni sehemu ndogo ambazo zina thamani sawa.

    Matofali ya fraction hutumika kama mfano muhimu wa sehemu ndogo sawa. Unaweza kutaka kutumia tiles sehemu ya kufanya shughuli zifuatazo. Au unaweza kufanya nakala ya Kielelezo 4.3 na kupanua ni pamoja na nane, kumi, na kumi na mbili.

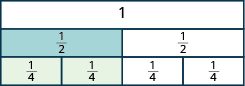
    Anza na\(\dfrac{1}{2}\) tile. Ngapi fourths sawa moja nusu? Ni wangapi wa\(\dfrac{1}{4}\) matofali hufunika\(\dfrac{1}{2}\) tile?

    Mstatili mmoja mrefu, usiogawanyika unaonyeshwa. Chini ni mstatili umegawanyika kwa vipande viwili, kila kinachoitwa kama nusu moja. Chini hiyo ni mstatili umegawanyika kwa wima katika vipande vinne, kila kinachoitwa kama moja ya nne.

    Kielelezo\(\PageIndex{7}\)

    Kwa kuwa\(\dfrac{1}{4}\) tiles mbili kufunika\(\dfrac{1}{2}\) tile, tunaona kwamba\(\dfrac{2}{4}\) ni sawa na\(\dfrac{1}{2}\), au\(\dfrac{2}{4} = \dfrac{1}{2}\).

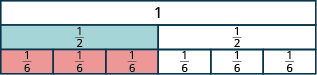
    Ni\(\dfrac{1}{6}\) tiles ngapi zinazofunika\(\dfrac{1}{2}\) tile?

    Mstatili mmoja mrefu, usiogawanyika unaonyeshwa. Chini ni mstatili umegawanyika kwa vipande viwili, kila kinachoitwa kama nusu moja. Chini hiyo ni mstatili umegawanyika kwa wima katika vipande sita, kila kinachoitwa kama moja ya sita.

    Kielelezo\(\PageIndex{8}\)

    Tangu\(\dfrac{1}{6}\) tiles tatu kufunika\(\dfrac{1}{2}\) tile, tunaona kwamba\(\dfrac{3}{6}\) ni sawa na\(\dfrac{1}{2}\). Hivyo,\(\dfrac{3}{6} = \dfrac{1}{2}\). Sehemu ndogo ni sehemu ndogo sawa.

    Mfano\(\PageIndex{13}\): equivalent fractions

    Tumia tiles za sehemu ili kupata sehemu ndogo sawa. Onyesha matokeo yako na takwimu.

    1. Ngapi eighths sawa moja nusu?
    2. Ngapi kumi sawa moja nusu?
    3. Ngapi twelfths sawa moja nusu?

    Suluhisho

    1. Inachukua\(\dfrac{1}{8}\) tiles nne ili kufunika\(\dfrac{1}{2}\) tile, hivyo\(\dfrac{4}{8} = \dfrac{1}{2}\).

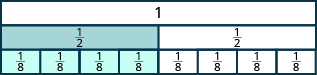
    Mstatili mmoja mrefu, usiogawanyika unaonyeshwa, ulioandikwa 1. Chini ni mstatili unaofanana umegawanyika kwa vipande viwili, kila kinachoitwa nusu 1. Chini hiyo ni mstatili unaofanana umegawanyika kwa vipande nane, kila kinachoitwa 1 nane.

    1. Inachukua\(\dfrac{1}{10}\) tiles tano ili kufunika\(\dfrac{1}{2}\) tile, hivyo\(\dfrac{5}{10} = \dfrac{1}{2}\).

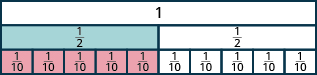
    Mstatili mmoja mrefu, usiogawanyika unaonyeshwa. Chini ni mstatili umegawanyika kwa vipande viwili, kila kinachoitwa kama nusu moja. Chini hiyo ni mstatili umegawanyika kwa wima katika vipande kumi, kila kinachoitwa kama moja ya kumi.

    1. Inachukua\(\dfrac{1}{12}\) tiles sita ili kufunika\(\dfrac{1}{2}\) tile, hivyo\(\dfrac{6}{12} = \dfrac{1}{2}\).

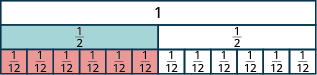
    Mstatili mmoja mrefu, usiogawanyika unaonyeshwa. Chini ni mstatili umegawanyika kwa vipande viwili, kila kinachoitwa kama nusu moja. Chini hiyo ni mstatili umegawanyika kwa wima katika vipande kumi na mbili, kila kinachoitwa kama moja ya kumi na mbili.

    Tuseme alikuwa tiles alama\(\dfrac{1}{20}\). Ngapi kati yao ingekuwa kuchukua kwa sawa\(\dfrac{1}{2}\)? Je, unafikiri tiles kumi? Kama wewe ni, wewe ni haki, kwa sababu\(\dfrac{10}{20} = \dfrac{1}{2}\).

    Tumeonyesha kuwa\(\dfrac{1}{2}, \dfrac{2}{4}, \dfrac{3}{6}, \dfrac{4}{8}, \dfrac{5}{10}, \dfrac{6}{12}\), na wote\(\dfrac{10}{20}\) ni sawa FRACTIONS.

    Zoezi\(\PageIndex{25}\)

    Matumizi tiles sehemu ya kupata FRACTIONS sawa: Ngapi themanths sawa moja ya nne?

    Jibu

    \(2\)

    Zoezi\(\PageIndex{26}\)

    Matumizi tiles sehemu ya kupata FRACTIONS sawa: Ngapi kumi na mbili sawa moja ya nne?

    Jibu

    \(3\)

    Pata FRACTIONS sawa

    Tulitumia tiles sehemu kuonyesha kwamba kuna sehemu nyingi sawa na\(\dfrac{1}{2}\). Kwa mfano,\(\dfrac{2}{4}, \dfrac{3}{6}\), na wote\(\dfrac{4}{8}\) ni sawa na\(\dfrac{1}{2}\). Tulipoweka tiles za sehemu, ilichukua nne za\(\dfrac{1}{8}\) matofali ili kufanya urefu sawa na\(\dfrac{1}{2}\) tile. Hii ilionyesha kuwa\(\dfrac{4}{8} = \dfrac{1}{2}\). Angalia Mfano\(\PageIndex{13}\).

    Tunaweza kuonyesha hii kwa pizzas, pia. Kielelezo\(\PageIndex{9a}\) kinaonyesha pizza moja, kata vipande viwili sawa na\(\dfrac{1}{2}\) kivuli. Kielelezo\(\PageIndex{9b}\) kinaonyesha pizza ya pili ya ukubwa sawa, kata vipande nane na\(\dfrac{4}{8}\) kivuli.

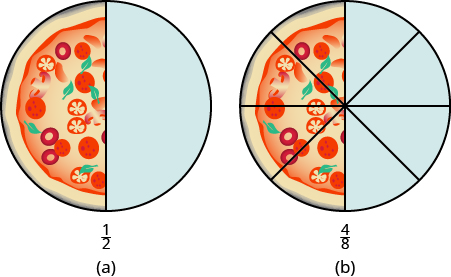
    Pizzas mbili zinaonyeshwa. Pizza upande wa kushoto imegawanywa katika vipande viwili sawa. Kipande 1 kimevuliwa. Pizza upande wa kulia imegawanywa katika vipande 8 sawa. Vipande 4 vimevuliwa.

    Kielelezo\(\PageIndex{9}\)

    Hii ni njia nyingine ya kuonyesha kwamba\(\dfrac{1}{2}\) ni sawa na\(\dfrac{4}{8}\). Tunawezaje kutumia hisabati kubadili\(\dfrac{1}{2}\)\(frac{4}{8}\)? Unawezaje kuchukua pizza iliyokatwa vipande viwili na kuikata vipande nane? Unaweza kukata kila moja ya vipande viwili kubwa katika vipande vinne vidogo! Pizza nzima ingekuwa kukatwa vipande nane badala ya mbili tu. Kihisabati, nini tumekuwa ilivyoelezwa inaweza kuandikwa kama:

    \[\dfrac{1 \cdot \textcolor{blue}{4}}{2 \cdot \textcolor{blue}{4}} = \dfrac{4}{8} \nonumber \]

    Mifano hizi husababisha Mali sawa ya sehemu, ambayo inasema kwamba ikiwa tunazidisha namba na denominator ya sehemu kwa idadi sawa, thamani ya sehemu haibadilika.

    Ufafanuzi: Sawa Fractions Mali

    Ikiwa\(a\),\(b\), na\(c\) ni namba wapi\(b ≠ 0\) na\(c ≠ 0\), basi

    \[\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c}\]

    Wakati wa kufanya kazi na sehemu ndogo, mara nyingi ni muhimu kuelezea sehemu sawa katika aina tofauti. Ili kupata aina sawa ya sehemu, tunaweza kutumia sawa Fractions Mali. Kwa mfano, fikiria sehemu moja ya nusu.

    \[\begin{split} \dfrac{1 \cdot \textcolor{blue}{3}}{2 \cdot \textcolor{blue}{3}} = \dfrac{3}{6} \; & so \; \dfrac{1}{2} = \dfrac{3}{6} \\ \dfrac{1 \cdot \textcolor{blue}{2}}{2 \cdot \textcolor{blue}{2}} = \dfrac{2}{4} \; & so \; \dfrac{1}{2} = \dfrac{2}{4} \\ \dfrac{1 \cdot \textcolor{blue}{10}}{2 \cdot \textcolor{blue}{10}} = \dfrac{10}{20} \; & so \; \dfrac{1}{2} = \dfrac{10}{20} \end{split} \nonumber \]

    Kwa hiyo, tunasema kwamba\(\dfrac{1}{2}, \dfrac{2}{4}, \dfrac{3}{6}\), na\(\dfrac{10}{20}\) ni sawa sehemu ndogo.

    Mfano\(\PageIndex{14}\): equivalent fractions

    Kupata sehemu tatu sawa na\(\dfrac{2}{5}\).

    Suluhisho

    Ili kupata sehemu sawa na\(\dfrac{2}{5}\), tunazidisha nambari na denominator kwa idadi sawa (lakini si sifuri). Hebu tuwazidishe kwa\(2\),\(3\), na\(5\).

    \[\dfrac{2 \cdot \textcolor{blue}{2}}{5 \cdot \textcolor{blue}{2}} = \dfrac{4}{10} \qquad \dfrac{2 \cdot \textcolor{blue}{3}}{5 \cdot \textcolor{blue}{3}} = \dfrac{6}{15} \qquad \dfrac{2 \cdot \textcolor{blue}{5}}{5 \cdot \textcolor{blue}{5}} = \dfrac{10}{25} \nonumber \]

    Hivyo,\(\dfrac{4}{10}, \dfrac{6}{15}\), na\(\dfrac{10}{25}\) ni sawa na\(\dfrac{2}{5}\).

    Zoezi\(\PageIndex{27}\)

    Kupata sehemu tatu sawa na\(\dfrac{3}{5}\).

    Jibu

    Majibu sahihi ni pamoja\(\dfrac{6}{10}, \dfrac{9}{15}\) na\(\dfrac{12}{20}\)

    Zoezi\(\PageIndex{28}\)

    Kupata sehemu tatu sawa na\(\dfrac{4}{5}\).

    Jibu

    Majibu sahihi ni pamoja\(\dfrac{8}{10}, \dfrac{12}{15}\) na\(\dfrac{16}{20}\)

    Mfano\(\PageIndex{15}\): equivalent fractions

    Kupata sehemu na denominator ya 21 kwamba ni sawa na\(\dfrac{2}{7}\).

    Suluhisho

    Ili kupata sehemu ndogo sawa, tunazidisha nambari na denominator kwa idadi sawa. Katika kesi hii, tunahitaji kuzidisha denominator kwa idadi ambayo itasababisha\(21\).

    Tangu tunaweza\(3\) kuzidisha\(7\) kwa kupata\(21\), tunaweza kupata sehemu sawa na kuzidisha wote numerator na denominator na\(3\).

    \[\dfrac{2}{7} = \dfrac{2 \cdot \textcolor{blue}{3}}{7 \cdot \textcolor{blue}{3}} = \dfrac{6}{21} \nonumber \]

    Zoezi\(\PageIndex{29}\)

    Kupata sehemu na denominator ya\(21\) kwamba ni sawa na\(\dfrac{6}{7}\).

    Jibu

    \(\dfrac{18}{21}\)

    Zoezi\(\PageIndex{30}\)

    Kupata sehemu na denominator ya\(100\) kwamba ni sawa na\(\dfrac{3}{10}\).

    Jibu

    \(\dfrac{30}{100}\)

    Pata sehemu ndogo na Hesabu zilizochanganywa kwenye Nambari ya Nambari

    Sasa tuko tayari kupanga njama kwenye mstari wa nambari. Hii itatusaidia kutazama sehemu ndogo na kuelewa maadili yao.

    Hebu Machapisho\(\dfrac{1}{5}, \dfrac{4}{5}, 3, 3 \dfrac{1}{3}, \dfrac{7}{4}, \dfrac{9}{2}, 5\), na\(\dfrac{8}{3}\) kwenye mstari wa nambari. Tutaanza na idadi nzima\(3\) na\(5\) kwa sababu ni rahisi kupanga njama.

    Mstari wa nambari unaonyeshwa na namba 3, 4, na 5. Kuna dots nyekundu saa 3 na saa 5.

    Sehemu ndogo zilizoorodheshwa ni\(\dfrac{1}{5}\) na\(\dfrac{4}{5}\). Tunajua FRACTIONS sahihi na maadili chini ya moja, hivyo\(\dfrac{1}{5}\) na\(\dfrac{1}{5}\) ziko kati ya idadi nzima\(0\) na\(1\). Denominators ni wote wawili\(5\), kwa hiyo tunahitaji kugawanya sehemu ya mstari wa namba kati\(0\) na\(1\) katika sehemu tano sawa. Tunaweza kufanya hivyo kwa kuchora alama nne sawa spaced juu ya mstari idadi, ambayo tunaweza kisha studio kama\(\dfrac{1}{5}, \dfrac{2}{5}, \dfrac{3}{5}\), na\(\dfrac{4}{5}\). Sasa njama inaelezea\(\dfrac{1}{5}\) na\(\dfrac{4}{5}\).

    Mstari wa nambari unaonyeshwa. Inaonyesha 0, 1 tano, 2 tano, 3 tano, 4 tano, na 1. Kuna dots nyekundu saa 1 ya tano na saa 4 tano.

    Nambari iliyochanganywa pekee ya kupanga njama ni\(3 \dfrac{1}{3}\). Kati ya nambari mbili zote ni\(3 \dfrac{1}{3}\)? Kumbuka kwamba idadi mchanganyiko ni namba nzima pamoja na sehemu sahihi, hivyo\(3 \dfrac{1}{3} > 3\). Kwa kuwa ni kubwa kuliko\(3\), lakini si kitengo nzima kubwa,\(3 \dfrac{1}{3}\) ni kati\(3\) na\(4\). Tunahitaji kugawanya sehemu ya mstari wa nambari kati\(3\) na\(4\) vipande vitatu sawa (theluthi) na njama\(3 \dfrac{1}{3}\) kwenye alama ya kwanza.

    Mstari wa nambari unaonyeshwa kwa namba nzima 0 kupitia 5. Kati ya 3 na 4, 3 na 1 ya tatu na 3 na 2 theluthi ni lebo. Kuna dot nyekundu saa 3 na 1 ya tatu.

    Hatimaye, angalia sehemu zisizofaa\(\dfrac{7}{4}, \dfrac{9}{2}\), na\(\dfrac{8}{3}\). Kuweka pointi hizi itakuwa rahisi ikiwa utabadilisha kila mmoja kwa namba iliyochanganywa.

    \[\dfrac{7}{4} = 1 \dfrac{3}{4}, \qquad \dfrac{9}{2} = 4 \dfrac{1}{2}, \qquad \dfrac{8}{3} = 2 \dfrac{2}{3} \nonumber \]

    Hapa ni mstari wa nambari na pointi zote zilizopangwa.

    Mstari wa nambari unaonyeshwa kwa namba nzima 0 kwa njia ya 6. Kati ya 0 na 1, 1 tano na 4 tano zimeandikwa na zinaonyeshwa kwa dots nyekundu. Kati ya 1 na 2, 7 nne ni lebo na kuonyeshwa kwa dot nyekundu. Kati ya 2 na 3, theluthi 8 imeandikwa na kuonyeshwa kwa dot nyekundu. Kati ya 3 na 4, 3 na 1 ya tatu ni kinachoitwa na kuonyeshwa kwa dot nyekundu. Kati ya 4 na 5, nusu 9 zimeandikwa na zinaonyeshwa kwa dot nyekundu.

    Mfano\(\PageIndex{16}\): locate and label

    Machapisho na lebo zifuatazo kwenye mstari namba:\(\dfrac{3}{4}, \dfrac{4}{3}, \dfrac{5}{3}, 4 \dfrac{1}{5}\), na\(\dfrac{7}{2}\).

    Suluhisho

    Anza kwa kupata sehemu sahihi\(\dfrac{3}{4}\). Ni kati ya\(0\) na\(1\). Kwa kufanya hivyo, ugawanye umbali kati\(0\) na\(1\) sehemu nne sawa. Kisha njama\(\dfrac{3}{4}\).

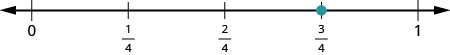
    Mstari wa nambari unaonyeshwa. Inaonyesha 0, 1 ya nne, 2 ya nne, 3 ya nne, na 1. Kuna dot nyekundu katika 3 nne.

    Kisha, tafuta nambari iliyochanganywa\(4 \dfrac{1}{5}\). Ni kati\(4\) na\(5\) kwenye mstari wa nambari. Gawanya mstari wa nambari kati\(4\) na\(5\) sehemu tano sawa, na kisha njama\(4 \dfrac{1}{5}\) moja ya tano ya njia kati\(4\) na\(5\).

    Mstari wa nambari unaonyeshwa. Inaonyesha 4, 4 na 1 tano, 4 na 2 tano, 4 na 3 tano, 4 na 4 tano, na 5. Kuna dot nyekundu saa 4 na 1 tano.

    Sasa Pata sehemu zisizofaa\(\dfrac{4}{3}\) na\(\dfrac{5}{3}\). Ni rahisi kuwapanga njama ikiwa tunawabadilisha kwa nambari zilizochanganywa kwanza.

    \[\dfrac{4}{3} = 1 \dfrac{1}{3}, \qquad \dfrac{5}{3} = 1 \dfrac{2}{3} \nonumber\]

    Gawanya umbali kati\(1\) na\(2\) ndani ya theluthi.

    Mstari wa nambari unaonyeshwa. Inaonyesha 1, 1 na 1 ya tatu, 1 na 2 theluthi, na 2. Chini ya 1 inasema theluthi 3. Chini ya 1 na 1 ya tatu inasema theluthi 4. Chini ya 1 na 2 theluthi inasema theluthi 5. Chini ya 2 inasema theluthi 6. Kuna dots nyekundu saa 1 na 1 ya tatu na 1 na 2 theluthi.

    Next hebu njama\(\dfrac{7}{2}\). Tunaandika kama nambari iliyochanganywa,\(\dfrac{7}{2} = 3 \dfrac{1}{2}\). Plot kati\(3\) na\(4\).

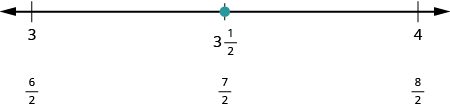
    Mstari wa nambari unaonyeshwa. Inaonyesha 3, 3 na 1 nusu, na 4. Chini ya 3 inasema nusu 6. Chini ya 3 na 1 nusu inasema nusu 7. Chini ya 4 inasema nusu 8. Kuna dot nyekundu saa 3 na 1 nusu.

    Mstari wa nambari unaonyesha namba zote ziko kwenye mstari wa nambari.

    Mstari wa nambari unaonyeshwa. Inaonyesha namba nzima 0 kwa njia ya 5. Kati ya idadi yoyote 2 ni alama 10 za kupe. Kati ya 0 na 1, kati ya alama ya 7 na ya 8 ya alama, 3 nne zimeandikwa na zinaonyeshwa kwa dot nyekundu. Kati ya 1 na 2, theluthi 4 na theluthi 5 zimeandikwa na zinaonyeshwa kwa dots nyekundu. Kati ya 3 na 4, nusu 7 zimeandikwa na zinaonyeshwa kwa dot nyekundu. Kati ya 4 na 5, 4 na 1 tano ni kinachoitwa na kuonyeshwa kwa dot nyekundu.

    Zoezi\(\PageIndex{31}\)

    Machapisho na studio yafuatayo kwenye mstari namba:\(\dfrac{1}{3}, \dfrac{5}{4}, \dfrac{7}{4}, 2 \dfrac{3}{5}, \dfrac{9}{2}\).

    Jibu

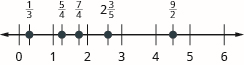
    Zoezi 4.1.31.png

    Zoezi\(\PageIndex{32}\)

    Machapisho na studio yafuatayo kwenye mstari namba:\(\dfrac{2}{3}, \dfrac{5}{2}, \dfrac{9}{4}, \dfrac{11}{4}, 3 \dfrac{2}{5}\).

    Jibu

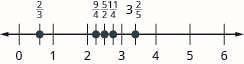
    Zoezi 4.1.32.png

    Katika Utangulizi wa Integers, sisi defined kinyume cha idadi. Ni namba ambayo ni umbali sawa kutoka sifuri kwenye mstari wa namba lakini upande wa pili wa sifuri. Tuliona, kwa mfano, kwamba kinyume cha\(7\) ni\(−7\) na kinyume cha\(−\) 7 ni\(7\).

    Mstari wa nambari unaonyeshwa. Inaonyesha namba hasi 7, 0 na 7. Kuna dots nyekundu katika hasi 7 na 7. Nafasi kati ya hasi 7 na 0 inaitwa kama vitengo 7. Nafasi kati ya 0 na 7 imeandikwa kama vitengo 7.

    Sehemu ndogo zina kupinga, pia. Kinyume cha\(\dfrac{3}{4}\) ni\(− \dfrac{3}{4}\). Ni umbali sawa kutoka\(0\) kwenye mstari namba, lakini upande wa pili wa\(0\).

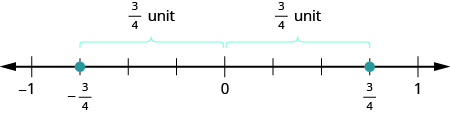
    Mstari wa nambari unaonyeshwa. Inaonyesha namba hasi 1, hasi 3 nne, 0, 3 nne, na 1. Kuna dots nyekundu katika hasi 3 nne na 3 nne. Nafasi kati ya nne hasi 3 na 0 inaitwa kama 3 ya nne ya kitengo. Nafasi kati ya 0 na 3 ya nne inaitwa kama 3 ya nne ya kitengo.

    Kufikiria sehemu ndogo hasi kama kinyume cha sehemu nzuri zitatusaidia kuzipata kwenye mstari wa nambari. Ili kupata\(− \dfrac{15}{8}\) kwenye mstari wa nambari, kwanza fikiria wapi\(\dfrac{15}{8}\) iko. Ni sehemu isiyofaa, kwa hiyo sisi kwanza tunaibadilisha kwa nambari iliyochanganywa\(1 \dfrac{7}{8}\) na kuona kwamba itakuwa kati\(1\) na\(2\) kwenye mstari wa nambari. Hivyo kinyume chake,\(− \dfrac{15}{8}\), itakuwa kati\(−1\) na\(−2\) kwenye mstari wa namba.

    Mstari wa nambari unaonyeshwa. Inaonyesha namba hasi 2, hasi 1, 0, 1, na 2. Kati ya hasi 2 na hasi 1, hasi 1 na 7 nane ni lebo na alama na dot nyekundu. Umbali kati ya hasi 1 na 7 nane na 0 ni alama kama vitengo 15 vya nane. Kati ya 1 na 2, 1 na 7 nane ni lebo na alama na dot nyekundu. Umbali kati ya 0 na 1 na 7 nane ni alama kama vitengo 15 vya nane.

    Mfano\(\PageIndex{17}\): locate and label

    Machapisho na lebo zifuatazo kwenye mstari namba:\(\dfrac{1}{4}, − \dfrac{1}{4}, 1 \dfrac{1}{3}, −1 \dfrac{1}{3}, \dfrac{5}{2}\), na\(− \dfrac{5}{2}\).

    Suluhisho

    Chora mstari wa nambari. Mark\(0\) katikati na kisha alama vitengo kadhaa upande wa kushoto na kulia.

    Ili kupata\(\dfrac{1}{4}\), ugawanye muda kati\(0\) na\(1\) katika sehemu nne sawa. Kila sehemu inawakilisha robo moja ya umbali. Hivyo njama\(\dfrac{1}{4}\) katika alama ya kwanza.

    Mstari wa nambari unaonyeshwa. Inaonyesha namba hasi 4, hasi 3, hasi 2, hasi 1, 0, 1, 2, 3, na 4. Kuna alama 4 za kupe kati ya hasi 1 na 0. Kuna alama 4 za kupe kati ya 0 na 1. Alama ya kwanza ya Jibu kati ya 0 na 1 imeandikwa kama 1 ya nne na imewekwa na dot nyekundu.

    Ili kupata\(− \dfrac{1}{4}\), ugawanye muda kati\(0\) na\(−1\) katika sehemu nne sawa. \(− \dfrac{1}{4}\)Plot katika alama ya kwanza kwa upande wa kushoto wa\(0\).

    Mstari wa nambari unaonyeshwa. Inaonyesha namba hasi 4, hasi 3, hasi 2, hasi 1, 0, 1, 2, 3, na 4. Kuna alama 4 za kupe kati ya hasi 1 na 0. Kuna alama 4 za kupe kati ya 0 na 1. Alama ya kwanza ya Jibu kati ya 0 na 1 imeandikwa kama 1 ya nne na imewekwa na dot nyekundu. Alama ya kwanza ya alama kati ya 0 na hasi 1 imeandikwa kama hasi 1 ya nne na imewekwa na dot nyekundu.

    Kwa kuwa\(1 \dfrac{1}{3}\) ni kati\(1\) na\(2\), kugawanya muda kati\(1\) na\(2\) katika sehemu tatu sawa. \(1 \dfrac{1}{3}\)Plot katika alama ya kwanza na haki ya\(1\). Kisha tangu\(−1 \dfrac{1}{3}\) ni kinyume chake\(1 \dfrac{1}{3}\) ni kati\(−1\) na\(−2\). Gawanya muda kati\(−1\) na\(−2\) katika sehemu tatu sawa. \(−1 \dfrac{1}{3}\)Plot katika alama ya kwanza kwa upande wa kushoto wa\(−1\).

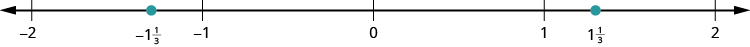
    Mstari wa nambari unaonyeshwa. Integers kutoka hasi 2 hadi 2 ni lebo. Kati ya hasi 2 na hasi 1, hasi 1 na 1 ya tatu ni lebo na alama na dot nyekundu. Kati ya 1 na 2, 1 na 1 ya tatu ni kinachoitwa na alama na dot nyekundu.

    Ili Machapisho\(\dfrac{5}{2}\) na\(− \dfrac{5}{2}\), inaweza kuwa na manufaa kuandika tena kama namba zilizochanganywa\(2 \dfrac{1}{2}\) na\(−2 \dfrac{1}{2}\). Kwa kuwa\(2 \dfrac{1}{2}\) ni kati\(2\) na\(3\), kugawanya muda kati\(2\) na\(3\) katika sehemu mbili sawa. \(\dfrac{5}{2}\)Panda kwenye alama. Kisha tangu\(−2 \dfrac{1}{2}\) ni kati\(−2\) na\(−3\), kugawanya muda kati\(−2\) na\(−3\) katika sehemu mbili sawa. \(− \dfrac{5}{2}\)Panda kwenye alama.

    Mstari wa nambari unaonyeshwa. Integers kutoka hasi 4 hadi 4 ni lebo. Kati ya hasi 3 na hasi 2, halves 5 hasi ni lebo na alama na dot nyekundu. Kati ya 2 na 3, nusu 5 ni lebo na alama na dot nyekundu.

    Zoezi\(\PageIndex{33}\)

    Machapisho na studio kila moja ya sehemu fulani kwenye mstari namba:\(\dfrac{2}{3}, − \dfrac{2}{3}, 2 \dfrac{1}{4}, −2 \dfrac{1}{4}, \dfrac{3}{2}, − \dfrac{3}{2}\)

    Jibu

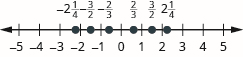
    Zoezi 4.1.33.png

    Zoezi\(\PageIndex{34}\)

    Machapisho na studio kila moja ya sehemu fulani kwenye mstari namba:\(\dfrac{3}{4}, − \dfrac{3}{4}, 1 \dfrac{1}{2}, −1 \dfrac{1}{2}, \dfrac{7}{3}, − \dfrac{7}{3}\)

    Jibu

    Zoezi 4.1.34.png

    Sehemu za Order na Hesabu Mchanganyiko

    Tunaweza kutumia alama za kukosekana kwa usawa ili sehemu ndogo. Kumbuka kwamba\(a > b\) ina maana kwamba\(a\) ni haki ya\(b\) juu ya mstari idadi. Tunapohamia kutoka kushoto kwenda kulia kwenye mstari wa nambari, maadili huongezeka.

    Mfano\(\PageIndex{18}\): order

    Agizo kila moja ya jozi zifuatazo za namba, kwa kutumia\(<\) au\(>\):

    1. \(− \dfrac{2}{3}\)____\(−1\)
    2. \(−3 \dfrac{1}{2}\)____\(−3\)
    3. \(− \dfrac{3}{7}\)____\(− \dfrac{3}{8}\)
    4. \(−2\)____\(− \dfrac{16}{9}\)

    Suluhisho

    1. \(− \dfrac{2}{3} > −1\)

    Mstari wa nambari unaonyeshwa. Integers kutoka hasi 3 hadi 3 ni lebo. Hasi 1 ni alama na dot nyekundu. Kati ya hasi 1 na 0, hasi 2 theluthi ni lebo na alama na dot nyekundu.

    1. \(−3 \dfrac{1}{2} < −3\)

    Mstari wa nambari unaonyeshwa. Integers kutoka hasi 4 hadi 4 ni lebo. Kuna dot nyekundu katika hasi 3. Kati ya hasi 4 na hasi 3, hasi 3 na nusu moja ni lebo na alama na dot nyekundu.

    1. \(− \dfrac{3}{7} < − \dfrac{3}{8}\)

    Mstari wa nambari unaonyeshwa. Nambari hasi 3, hasi 2, hasi 1, 0, 1, 2, na 3 zimeandikwa. Kati ya hasi 1 na 0, hasi 3 saba na hasi 3 nane zimeandikwa na alama na dots nyekundu.

    1. \(−2 < − \dfrac{16}{9}\)

    Mstari wa nambari unaonyeshwa. Nambari hasi 3, hasi 2, hasi 1, 0, 1, 2, na 3 zimeandikwa. Kuna dot nyekundu katika hasi 2. Kati ya hasi 2 na hasi 1, hasi 16 juu ya 9 ni lebo na alama na dot nyekundu.

    Zoezi\(\PageIndex{35}\)

    Agizo kila moja ya jozi zifuatazo za namba, kwa kutumia\(<\) au\(>\):

    1. \(− \dfrac{1}{3}\)__\(−1\)
    2. \(−1 \dfrac{1}{2}\)__\(− 2\)
    3. \(− \dfrac{2}{3}\)__\(− \dfrac{1}{3}\)
    4. \(−3\)__\(− \dfrac{7}{3}\)
    Jibu

    \(>\)

    Jibu b

    \(>\)

    Jibu c

    \(<\)

    Jibu d

    \(<\)

    Zoezi\(\PageIndex{36}\)

    Agizo kila moja ya jozi zifuatazo za namba, kwa kutumia\(<\) au\(>\):

    1. \(−3\)__\(− \dfrac{17}{5}\)
    2. \(−2 \dfrac{1}{4}\)__\(−2\)
    3. \(− \dfrac{3}{5}\)__\(− \dfrac{4}{5}\)
    4. \(−4\)__\(− \dfrac{10}{3}\)
    Jibu

    \(>\)

    Jibu b

    \(<\)

    Jibu c

    \(>\)

    Jibu d

    \(<\)

    Dhana muhimu

    • Mali ya Mmoja
      • Nambari yoyote, isipokuwa sifuri, imegawanywa na yenyewe ni moja.
        \(\dfrac{a}{a}=1\), wapi\(a\neq 0\).
    • Mchanganyiko Hesabu
      • idadi mchanganyiko lina idadi nzima\(a\) na sehemu\(\dfrac{b}{c}\) ambapo\(c \neq 0\).
      • Imeandikwa kama ifuatavyo:\(a\dfrac{b}{c}\)\(c \neq 0\)
    • Vipande vilivyofaa na visivyofaa
      • Sehemu\(\frac{a}{b}\) ni sehemu sahihi ikiwa\(a<b\) na sehemu isiyofaa ikiwa\(a \geq b\).
    • Badilisha sehemu isiyofaa kwa nambari iliyochanganywa.
      1. Gawanya denominator ndani ya nambari.
      2. Tambua quotient, salio, na mgawanyiko.
      3. Andika nambari iliyochanganywa kama\(\dfrac{\text{remainder}}{\text{divisor}}\).
    • Badilisha nambari iliyochanganywa kwa sehemu isiyofaa.
      1. Panua idadi nzima kwa denominator.
      2. Ongeza nambari kwa bidhaa iliyopatikana katika Hatua ya 1.
      3. Andika jumla ya mwisho juu ya denominator ya awali.
    • Sawa FRACTIONS Mali
      • Ikiwa\(a\),\(b\) na\(c\) ni namba ambapo\(b \neq 0\)\(c \neq 0\), basi\ (\ dfrac {a} {b} =\ dfrac {a\ cdot c} {b\ cdot c}\]).

    faharasa

    sehemu sawa

    Sehemu sawa ni sehemu mbili au zaidi ambazo zina thamani sawa.

    sehemu

    Sehemu\(\dfrac{a}{b}\) imeandikwa. katika sehemu,\(a\) ni nambari na\(b\) ni denominator. Sehemu inawakilisha sehemu ya nzima. Denominator\(b\) ni idadi ya sehemu sawa ambazo zote zimegawanywa, na namba\(a\) inaonyesha sehemu ngapi zinajumuishwa.

    idadi mchanganyiko

    idadi mchanganyiko lina idadi nzima\(a\) na sehemu\(\dfrac{b}{c}\) ambapo\(c \neq 0\). Imeandikwa kama\(a\dfrac{b}{c}\), ambapo\(c \neq 0\).

    vipande sahihi na visivyofaa

    Sehemu hiyo\(\dfrac{a}{b}\) ni sahihi ikiwa\(a<b\) na haifai ikiwa\(a>b\).

    Mazoezi hufanya kamili

    1. Kwa sehemu “a”, mduara umegawanywa katika vipande 4 sawa. Kipande 1 kimevuliwa. Katika sehemu “b”, mduara umegawanywa katika vipande 4 sawa. Vipande 3 vimevuliwa. Katika sehemu ya “c”, mduara umegawanywa katika vipande 8 sawa. Vipande 3 vimevuliwa. Katika sehemu “d”, mduara umegawanywa katika vipande 8 sawa. Vipande 5 vimevuliwa.
    2. Kwa sehemu “a”, mduara umegawanywa katika vipande 12 sawa. Vipande 7 vimevuliwa. Katika sehemu “b”, mduara umegawanywa katika vipande 12 sawa. Vipande 5 vimevuliwa. Katika sehemu ya “c”, mraba umegawanywa katika vipande 9 sawa. 4 ya vipande ni kivuli. Katika sehemu “d”, mraba umegawanywa katika vipande 9 sawa. Vipande 5 vimevuliwa.

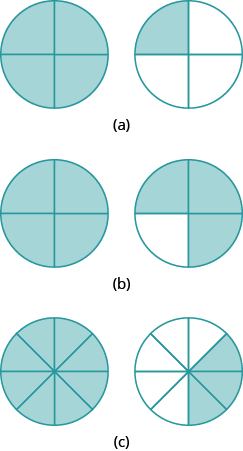
    Katika mazoezi yafuatayo, sehemu za kivuli za miduara au mraba ili kuiga sehemu ndogo zifuatazo.

    1. \(\dfrac{1}{2}\)
    2. \(\dfrac{1}{3}\)
    3. \(\dfrac{3}{4}\)
    4. \(\dfrac{2}{5}\)
    5. \(\dfrac{5}{6}\)
    6. \(\dfrac{7}{8}\)
    7. \(\dfrac{5}{8}\)
    8. \(\dfrac{7}{10}\)

    Katika mazoezi yafuatayo, tumia miduara ya sehemu ili kufanya wholes, ikiwa inawezekana, na vipande vifuatavyo.

    1. Theluthi 3
    2. 8 ya nane
    3. 7 ya sita
    4. Theluthi 4
    5. 7 tano
    6. 7 ya nne

    Katika mazoezi yafuatayo, jina la sehemu zisizofaa. Kisha kuandika kila sehemu isiyofaa kama nambari iliyochanganywa.

    1. Katika sehemu “a”, miduara miwili inavyoonyeshwa. Kila mmoja imegawanywa katika vipande 4 sawa. Mduara upande wa kushoto una vipande vyote vinne vilivyovuliwa. Mduara upande wa kulia una kipande 1 kivuli. Katika sehemu “b”, miduara miwili inavyoonyeshwa. Kila mmoja imegawanywa katika vipande 4 sawa. Mduara upande wa kushoto una vipande vyote vinne vilivyovuliwa. Mduara upande wa kulia una vipande 3 vilivyovuliwa. Katika sehemu “c”, miduara miwili inavyoonyeshwa. Kila mmoja imegawanywa katika vipande 8 sawa. Mduara upande wa kushoto una vipande vyote 8 vimevuliwa. Mduara upande wa kulia una vipande 3 vilivyovuliwa.
    2. Katika sehemu “a”, miduara 2 inavyoonyeshwa. Kila mmoja imegawanywa katika vipande 8 sawa. Mduara upande wa kushoto una vipande vyote 8 vimevuliwa. Mduara upande wa kulia una kipande 1 kivuli. Katika sehemu “b”, mraba miwili huonyeshwa. Kila mmoja imegawanywa katika vipande 4 sawa. Mraba upande wa kushoto una vipande vyote vinne vilivyovuliwa. Mduara upande wa kulia una kipande 1 kivuli. Katika sehemu “c”, mraba miwili huonyeshwa. Kila mmoja imegawanywa katika vipande 9 sawa. Mraba upande wa kushoto una vipande vyote 9 vimevuliwa. Mraba upande wa kulia una vipande viwili vilivyovuliwa.
    3. Katika sehemu “a”, miduara 3 inavyoonyeshwa. Kila mmoja imegawanywa katika vipande 4 sawa. Miduara miwili ya kwanza ina vipande vyote vinne vimevuliwa. Mduara wa tatu una vipande 3 vilivyovuliwa. Katika sehemu “b”, miduara 3 inavyoonyeshwa. Kila mmoja imegawanywa katika vipande 8 sawa. Miduara miwili ya kwanza ina vipande vyote 8 vimevuliwa. Mduara wa tatu una vipande 3 vilivyovuliwa.

    Katika mazoezi yafuatayo, futa miduara ya sehemu ili kuiga sehemu iliyotolewa.

    1. \(\dfrac{3}{3}\)
    2. \(\dfrac{4}{4}\)
    3. \(\dfrac{7}{4}\)
    4. \(\dfrac{5}{3}\)
    5. \(\dfrac{11}{6}\)
    6. \(\dfrac{13}{8}\)
    7. \(\dfrac{10}{3}\)
    8. \(\dfrac{9}{4}\)

    Katika mazoezi yafuatayo, fungua upya sehemu isiyofaa kama nambari iliyochanganywa.

    1. \(\dfrac{3}{2}\)
    2. \(\dfrac{5}{3}\)
    3. \(\dfrac{11}{4}\)
    4. \(\dfrac{13}{5}\)
    5. \(\dfrac{25}{6}\)
    6. \(\dfrac{28}{9}\)
    7. \(\dfrac{42}{13}\)
    8. \(\dfrac{47}{15}\)

    Katika mazoezi yafuatayo, fungua upya nambari iliyochanganywa kama sehemu isiyofaa.

    1. \(1 \dfrac{2}{3}\)
    2. \(1 \dfrac{2}{5}\)
    3. \(2 \dfrac{1}{4}\)
    4. \(2 \dfrac{5}{6}\)
    5. \(2 \dfrac{7}{9}\)
    6. \(2 \dfrac{5}{7}\)
    7. \(3 \dfrac{4}{7}\)
    8. \(3 \dfrac{5}{9}\)

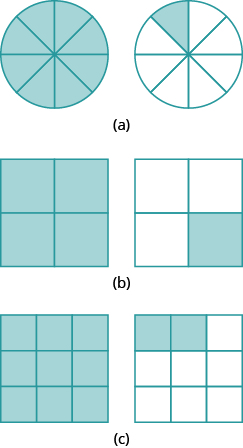
    Katika mazoezi yafuatayo, tumia tiles za sehemu au kuteka takwimu ili kupata sehemu ndogo sawa.

    1. Ngapi sixths sawa moja ya tatu?
    2. Ngapi twelfths sawa moja ya tatu?
    3. Ngapi themanths sawa tatu-fourths?
    4. Ngapi kumi na mbili sawa tatu-fourths?
    5. Ni ngapi nne sawa na halves tatu?
    6. Ngapi sixths sawa na nusu tatu?

    Katika mazoezi yafuatayo, pata sehemu tatu sawa na sehemu iliyotolewa. Onyesha kazi yako, kwa kutumia takwimu au algebra.

    1. \(\dfrac{1}{4}\)
    2. \(\dfrac{1}{3}\)
    3. \(\dfrac{3}{8}\)
    4. \(\dfrac{5}{6}\)
    5. \(\dfrac{2}{7}\)
    6. \(\dfrac{5}{9}\)

    Katika mazoezi yafuatayo, njama namba kwenye mstari wa nambari.

    1. \(\dfrac{2}{3}, \dfrac{5}{4}, \dfrac{12}{5}\)
    2. \(\dfrac{1}{3}, \dfrac{7}{4}, \dfrac{13}{5}\)
    3. \(\dfrac{1}{4}, \dfrac{9}{5}, \dfrac{11}{3}\)
    4. \(\dfrac{7}{10}, \dfrac{5}{2}, \dfrac{13}{8}, 3\)
    5. \(2 \dfrac{1}{3}, −2 \dfrac{1}{3}\)
    6. \(1 \dfrac{3}{4}, −1 \dfrac{3}{5}\)
    7. \(\dfrac{3}{4}, − \dfrac{3}{4}, 1 \dfrac{2}{3}, −1 \dfrac{2}{3}, \dfrac{5}{2}, − \dfrac{5}{2}\)
    8. \(\dfrac{2}{5}, − \dfrac{2}{5}, 1 \dfrac{3}{4}, −1 \dfrac{3}{4}, \dfrac{8}{3}, − \dfrac{8}{3}\)

    Katika mazoezi yafuatayo, tengeneza kila jozi zifuatazo za namba, ukitumia < or >.

    1. -1__\(− \dfrac{1}{4}\)
    2. -1__\(− \dfrac{1}{3}\)
    3. \(−2 \dfrac{1}{2}\)__3
    4. \(−1 \dfrac{3}{4}\)__2
    5. \(− \dfrac{5}{12}\)__\(− \dfrac{7}{12}\)
    6. \(− \dfrac{9}{10}\)__\(− \dfrac{3}{10}\)
    7. -3__\(− \dfrac{13}{5}\)
    8. -4__\(− \dfrac{23}{6}\)

    kila siku Math

    1. Muziki Hatua Ngoma ya choreographed imevunjwa katika makosa. \(\dfrac{1}{1}\)Hesabu ina hatua moja katika hesabu,\(\dfrac{1}{2}\) hesabu ina hatua mbili katika hesabu na hesabu ya 1 3 ina hatua tatu katika hesabu. Ni hatua ngapi zingekuwa katika\(\dfrac{1}{5}\) hesabu? Ni aina gani ya hesabu ina hatua nne ndani yake?
    2. Muziki Hatua Fractions hutumiwa mara nyingi katika muziki. Katika muda wa 4 4, kuna maelezo ya robo nne kwa kipimo kimoja.
      1. Ni hatua ngapi bila maelezo ya robo nane kufanya?
      2. Wimbo wa “Happy Birthday to You” una maelezo ya robo 25. Kuna hatua ngapi katika “Furaha ya Kuzaliwa kwako?”
    3. Baking Nina ni kufanya sufuria tano ya fudge kutumikia baada ya recital muziki. Kwa kila sufuria, anahitaji 1 2 kikombe cha walnuts.
      1. Ni vikombe ngapi vya walnuts anahitaji kwa sufuria tano za fudge?
      2. Je! Unafikiri ni rahisi kupima kiasi hiki unapotumia sehemu isiyofaa au nambari iliyochanganywa? Kwa nini?

    Mazoezi ya kuandika

    1. Kutoa mfano kutoka kwa uzoefu wako wa maisha (nje ya shule) ambapo ilikuwa muhimu kuelewa sehemu ndogo.
    2. Eleza jinsi Machapisho sehemu\(\dfrac{21}{4}\) yasiyofaa kwenye mstari namba ambayo tu namba nzima kutoka 0 kwa njia ya 10 ni alama.

    Self Check

    (a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

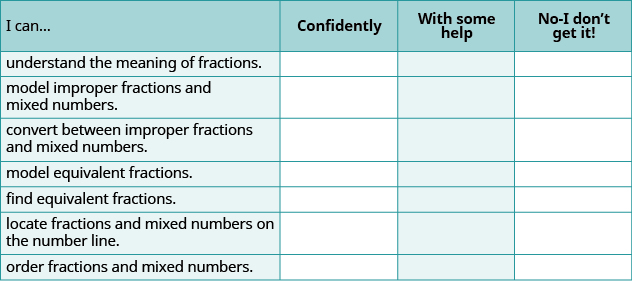
    (b) Kama wengi wa hundi yako walikuwa:

    ... kwa ujasiri. Hongera! Umefanikiwa malengo katika sehemu hii. Fikiria ujuzi wa kujifunza uliyotumia ili uweze kuendelea kuitumia. Ulifanya nini ili uwe na ujasiri wa uwezo wako wa kufanya mambo haya? Kuwa maalum.

    ... kwa msaada fulani. Hii lazima kushughulikiwa haraka kwa sababu mada huna bwana kuwa mashimo katika barabara yako ya mafanikio. Katika hesabu, kila mada hujenga juu ya kazi ya awali. Ni muhimu kuhakikisha kuwa na msingi imara kabla ya kuendelea. Nani unaweza kuomba msaada? Washiriki wenzako na mwalimu ni rasilimali nzuri. Je, kuna mahali kwenye chuo ambapo waalimu hisabati zinapatikana? Je, ujuzi wako wa kujifunza unaweza kuboreshwa?

    ... hakuna-siipati! Hii ni ishara ya onyo na haipaswi kupuuza. Unapaswa kupata msaada mara moja au utazidiwa haraka. Angalia mwalimu wako haraka iwezekanavyo kujadili hali yako. Pamoja unaweza kuja na mpango wa kupata msaada unayohitaji.

    Wachangiaji na Majina