Skip to main content
Global

4.1: Tazama sehemu ndogo (Sehemu ya 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    173387

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Kuelewa maana ya sehemu ndogo
    • Mfano wa vipande visivyofaa na namba zilizochanganywa
    • Badilisha kati ya sehemu zisizofaa na namba zilizochanganywa
    • Mfano sawa sehemu
    • Pata sehemu ndogo sawa
    • Pata sehemu ndogo na namba zilizochanganywa kwenye mstari wa nambari
    • Sehemu ndogo na nambari zilizochanganywa
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kurahisisha:\(5 • 2 + 1\). Ikiwa umekosa tatizo hili, kagua Mfano 2.1.8.
    2. Jaza tupu na\(<\) au\(>\):\(−2\) __\(−5\). Ikiwa umekosa tatizo hili, tathmini Mfano 3.1.2.

    Kuelewa Maana ya FRACTIONS

    Andy na Bobby upendo pizza. Jumatatu usiku, wanashiriki pizza sawa. Ni kiasi gani cha pizza ambacho kila mmoja hupata? Je, unafikiri kwamba kila kijana anapata nusu ya pizza? Hiyo ni kweli. Kuna pizza moja nzima, sawasawa imegawanywa katika sehemu mbili, hivyo kila kijana anapata moja ya sehemu mbili sawa. Katika hesabu, tunaandika\(\dfrac{1}{2}\) kwa maana moja kati ya sehemu mbili.

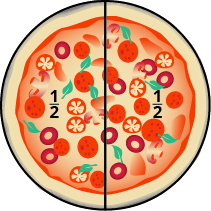
    Picha ya pizza ya pande zote iliyokatwa kwa wima katikati, na kujenga vipande viwili sawa. Kila kipande kinachoitwa kama nusu moja.

    Kielelezo\(\PageIndex{1}\)

    Siku ya Jumanne, Andy na Bobby wanashiriki pizza na wazazi wao, Fred na Christy, na kila mtu kupata kiasi sawa cha pizza nzima. Ni kiasi gani cha pizza ambacho kila mtu hupata? Kuna pizza moja nzima, imegawanywa sawasawa katika sehemu nne sawa. Kila mtu ana moja ya sehemu nne sawa, hivyo kila mmoja ana\(\dfrac{1}{4}\) ya pizza.

    Picha ya pizza ya pande zote iliyokatwa kwa wima na kwa usawa, na kujenga vipande vinne sawa. Kila kipande kinachoitwa kama moja ya nne.

    Kielelezo\(\PageIndex{2}\)

    Siku ya Jumatano, familia inakaribisha marafiki wengine juu ya chakula cha jioni cha pizza. Kuna jumla ya\(12\) watu. Kama kushiriki pizza sawa, kila mtu kupata\(\dfrac{1}{12}\) ya pizza.

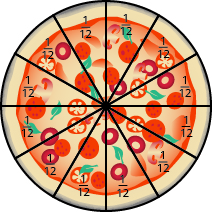
    Picha ya pizza pande zote iliyokatwa katika wedges kumi na mbili sawa. Kila kipande kinachoitwa kama moja ya kumi na mbili.

    Kielelezo\(\PageIndex{3}\)

    Ufafanuzi: Fractions

    Sehemu imeandikwa\(\dfrac{a}{b}\), wapi\(a\) na\(b\) ni integers na\(b ≠ 0\). Katika sehemu,\(a\) inaitwa nambari na\(b\) inaitwa denominator.

    Sehemu ni njia ya kuwakilisha sehemu nzima. Denominator\(b\) inawakilisha idadi ya sehemu sawa ambazo zote zimegawanywa, na namba\(a\) inawakilisha sehemu ngapi zinajumuishwa. Denominator,\(b\), haiwezi sawa na sifuri kwa sababu mgawanyiko kwa sifuri haujafafanuliwa.

    Katika Kielelezo\(\PageIndex{4}\), mduara umegawanywa katika sehemu tatu za ukubwa sawa. Kila sehemu inawakilisha\(\dfrac{1}{3}\) mduara. Aina hii ya mfano inaitwa mduara wa sehemu. Maumbo mengine, kama vile rectangles, yanaweza pia kutumika kutengeneza sehemu ndogo.

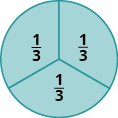
    Mzunguko umegawanywa katika wedges tatu sawa. Kila kipande kinachoitwa kama theluthi moja.

    Kielelezo\(\PageIndex{4}\)

    Sehemu hiyo\(\dfrac{2}{3}\) inawakilisha nini? Sehemu\(\dfrac{2}{3}\) ina maana mbili ya sehemu tatu sawa.

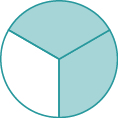
    Mzunguko umegawanywa katika wedges tatu sawa. Mbili ya wedges ni kivuli.

    Kielelezo\(\PageIndex{5}\)

    Mfano\(\PageIndex{1}\): name the fraction

    Jina sehemu ya sura iliyofunikwa katika kila takwimu.

    1. Katika sehemu “a”, mduara umegawanywa katika wedges nane sawa. Tano ya wedges ni kivuli. Katika sehemu “b”, mraba umegawanywa katika vipande tisa sawa. Vipande viwili ni kivuli.
    2. Katika sehemu “a”, mduara umegawanywa katika wedges nane sawa. Tano ya wedges ni kivuli. Katika sehemu “b”, mraba umegawanywa katika vipande tisa sawa. Vipande viwili ni kivuli.

    Suluhisho

    Tunahitaji kuuliza maswali mawili. Kwanza, ni sehemu ngapi sawa? Hii itakuwa denominator. Pili, ya sehemu hizi sawa, wangapi ni kivuli? Hii itakuwa namba.

    Ni sehemu ngapi sawa zipo? Kuna sehemu nane sawa.
    Ni wangapi wamevuliwa? Sehemu tano ni kivuli.

    Sehemu tano kati ya nane zimefunikwa. Kwa hiyo, sehemu ya mduara ambayo ni kivuli ni\(\dfrac{5}{8}\).

    Ni sehemu ngapi sawa zipo? Kuna sehemu tisa sawa.
    Ni wangapi wamevuliwa? Sehemu mbili ni kivuli.

    Sehemu mbili kati ya tisa zimefunikwa. Kwa hiyo, sehemu ya mraba ambayo ni kivuli ni\(\dfrac{2}{9}\).

    Zoezi\(\PageIndex{1}\)

    Jina sehemu ya sura iliyo kivuli katika kila takwimu:

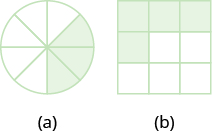
    Katika sehemu “a”, mduara umegawanywa katika wedges nane sawa. Tatu ya wedges ni kivuli. Katika sehemu “b”, mraba umegawanywa katika vipande tisa sawa. Vipande vinne ni kivuli.

    Jibu

    \(\dfrac{3}{8}\)

    Jibu b

    \(\dfrac{4}{9}\)

    Zoezi\(\PageIndex{2}\)

    Jina sehemu ya sura iliyo kivuli katika kila takwimu:

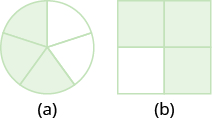
    Katika sehemu “a”, mduara umegawanywa katika wedges tano sawa. Tatu ya wedges ni kivuli. Katika sehemu “b”, mraba umegawanywa katika vipande vinne sawa. Vipande vitatu ni kivuli.

    Jibu

    \(\dfrac{3}{5}\)

    Jibu b

    \(\dfrac{3}{4}\)

    Mfano\(\PageIndex{2}\):

    Kivuli\(\dfrac{3}{4}\) cha mduara.

    Picha ya mduara.

    Suluhisho

    Denominator ni\(4\), hivyo tunagawanya mduara katika sehemu nne sawa (a). Nambari ni\(3\), hivyo sisi kivuli tatu ya sehemu nne (b).

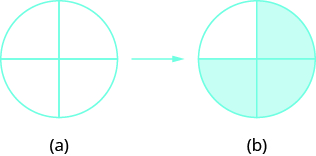
    Katika “a”, mduara unaonyeshwa umegawanywa katika vipande vinne sawa. Mshale unaonyesha kutoka “a” hadi “b”. Katika “b”, picha hiyo inavyoonyeshwa na vipande vitatu vilivyovuliwa.

    \(\dfrac{3}{4}\)ya mduara ni kivuli.

    Zoezi\(\PageIndex{3}\)

    Kivuli\(\dfrac{6}{8}\) cha mduara.

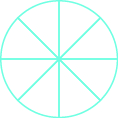
    Mduara umegawanywa katika vipande nane sawa.

    Jibu

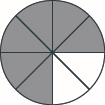
    Zoezi 4.1.3.png

    Zoezi\(\PageIndex{4}\)

    Kivuli\(\dfrac{2}{5}\) cha mstatili.

    Mstatili umegawanyika kwa wima katika vipande vitano sawa.

    Jibu

    Zoezi 4.1.4.png

    Katika Mfano\(\PageIndex{1}\) na Mfano\(\PageIndex{2}\), tulitumia miduara na rectangles kutengeneza sehemu ndogo. Fractions pia inaweza kuwa inatokana kama manipulatives kuitwa sehemu tiles, kama inavyoonekana katika Kielelezo\(\PageIndex{6}\). Hapa, yote inaelekezwa kama tile moja ya muda mrefu, isiyogawanyika ya mstatili. Chini yake ni tiles ya urefu sawa kugawanywa katika idadi tofauti ya sehemu sawa ukubwa.

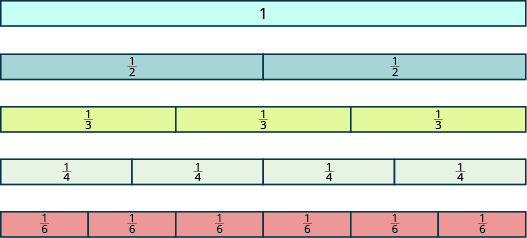
    Tile moja ya muda mrefu, isiyogawanyika ya mstatili imeonyeshwa, iliyoandikwa “1”. Chini ni tile ya mstatili wa ukubwa sawa na sura ambayo imegawanywa kwa wima katika vipande viwili sawa, kila kinachoitwa kama nusu moja. Chini hiyo ni tile nyingine ya mstatili ambayo imegawanywa katika vipande vitatu sawa, kila kinachoitwa kama theluthi moja. Chini hiyo ni tile nyingine ya mstatili ambayo imegawanywa katika vipande vinne sawa, kila kinachoitwa kama moja ya nne. Chini hiyo ni tile nyingine ya mstatili ambayo imegawanywa katika vipande sita, kila kinachoitwa kama moja ya sita.

    Kielelezo\(\PageIndex{6}\)

    Tutaweza kutumia tiles sehemu kugundua baadhi ya ukweli wa msingi kuhusu sehemu ndogo. Rejea Kielelezo\(\PageIndex{6}\) kujibu maswali yafuatayo:

    Je! Inachukua\(\dfrac{1}{2}\) tiles ngapi ili kufanya tile moja nzima? Inachukua nusu mbili kufanya nzima, hivyo mbili kati ya mbili ni\(\dfrac{2}{2}\) = 1.
    Je! Inachukua\(\dfrac{1}{3}\) tiles ngapi ili kufanya tile moja nzima? Inachukua theluthi tatu, hivyo tatu kati ya tatu ni\(\dfrac{3}{3}\) = 1.
    Je! Inachukua\(\dfrac{1}{4}\) tiles ngapi ili kufanya tile moja nzima? Inachukua nne nne, hivyo nne kati ya nne ni\(\dfrac{4}{4}\) = 1.
    Je! Inachukua\(\dfrac{1}{5}\) tiles ngapi ili kufanya tile moja nzima? Inachukua sita sita, hivyo sita kati ya sita ni\(\dfrac{6}{6}\) = 1.
    Nini ikiwa wote waligawanywa katika sehemu 24 sawa? (Sisi si umeonyesha vigae sehemu kuwakilisha hii, lakini jaribu taswira yake katika akili yako.) Je! Inachukua\(\dfrac{1}{24}\) tiles ngapi ili kufanya tile moja nzima? Inachukua 24 ishirini na nne, hivyo\(\dfrac{24}{24}\) = 1.

    Inachukua\(24\) ishirini na nne, hivyo\(\dfrac{24}{24} = 1\). Hii inatuongoza kwenye Mali ya Mmoja.

    Ufafanuzi: Mali ya Mmoja

    Nambari yoyote, isipokuwa sifuri, imegawanywa na yenyewe ni moja.

    \[\dfrac{a}{a} = 1 \qquad \qquad (a \neq 0)\]

    Mfano\(\PageIndex{3}\): fraction circles to form wholes

    Tumia miduara ya sehemu ili kufanya wholes kutumia vipande vifuatavyo:

    1. \(4\)ya nne
    2. \(5\)tano
    3. \(6\)ya sita

    Suluhisho

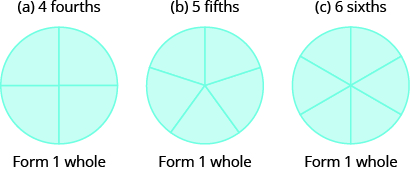
    Miduara mitatu inavyoonyeshwa. Mduara upande wa kushoto umegawanywa katika vipande vinne sawa. Mduara katikati umegawanywa katika vipande vitano sawa. Mduara upande wa kulia umegawanywa katika vipande sita sawa. Kila mduara unasema “Fomu 1 nzima” chini yake.

    Zoezi\(\PageIndex{5}\)

    Tumia miduara ya sehemu ili kufanya wholes na vipande vifuatavyo:\(3\) theluthi.

    Jibu

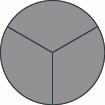
    Zoezi 4.1.5.png

    Zoezi\(\PageIndex{6}\)

    Tumia miduara ya sehemu ili kufanya wholes na vipande vifuatavyo:\(8\) nane.

    Jibu

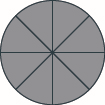
    Zoezi 4.1.6.png

    Nini kama tuna vipande sehemu zaidi ya tunahitaji kwa\(1\) ujumla? Tutaangalia hili katika mfano unaofuata.

    Mfano\(\PageIndex{4}\): fraction circles to form whole

    Tumia miduara ya sehemu ili kufanya wholes kutumia vipande vifuatavyo:

    1. \(3\)nusu
    2. \(8\)tano
    3. \(7\)theluthi

    Suluhisho

    1. \(3\)nusu kufanya\(1\) nzima na\(1\) nusu kushoto juu.

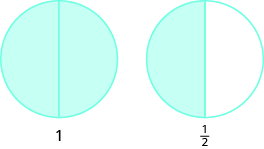
    Duru mbili zinaonyeshwa, zote mbili zimegawanywa katika vipande viwili sawa. Mduara upande wa kushoto una vipande vyote vilivyovuliwa na huitwa kama “1”. Mduara upande wa kulia una kipande kimoja kivuli na kinachoitwa kama nusu moja.

    1. \(8\)tano kufanya\(1\) nzima na\(3\) tano kushoto juu.

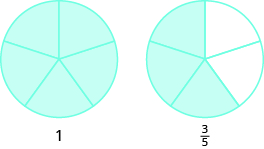
    Duru mbili zinaonyeshwa, zote mbili zimegawanywa katika vipande vitano sawa. Mduara upande wa kushoto una vipande vyote vitano vilivyovuliwa na huitwa kama “1”. Mduara upande wa kulia una vipande vitatu vilivyovuliwa na huitwa kama tano tatu.

    1. \(7\)theluthi kufanya\(2\) wholes na\(1\) tatu kushoto juu.

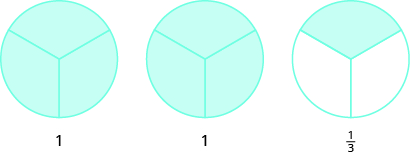
    Duru tatu zinaonyeshwa, zote zimegawanywa katika vipande vitatu sawa. Miduara miwili upande wa kushoto ina vipande vyote vitatu vilivyovuliwa na vimeandikwa na wale. Mduara upande wa kulia una kipande kimoja kivuli na kinachoitwa kama theluthi moja.

    Zoezi\(\PageIndex{7}\)

    Tumia miduara ya sehemu ili kufanya wholes na vipande vifuatavyo:\(5\) theluthi.

    Jibu

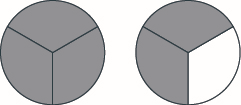
    Zoezi 4.1.7.png

    Zoezi\(\PageIndex{8}\)

    Tumia miduara ya sehemu ili kufanya wholes na vipande vifuatavyo:\(5\) nusu.

    Jibu

    Zoezi 4.1.8.png

    Sehemu zisizofaa za mfano na Hesabu zilizochanganywa

    Katika Mfano\(\PageIndex{4b}\), ulikuwa na vipande nane sawa vya tano. Ulikuwa na tano kati yao kufanya moja nzima, na ulikuwa na tano tatu kushoto juu. Hebu kutumia sehemu nukuu kuonyesha nini kilichotokea. Nyinyi mlikuwa na vipande vinane, kila moja ya tano\(\dfrac{1}{5}\), kwa hiyo mlikuwa na tano nane, ambazo tunaweza kuandika kama vile\(\dfrac{8}{5}\). Sehemu\(\dfrac{8}{5}\) ni moja nzima\(1\), pamoja na tano tatu,, au\(\dfrac{3}{5}\)\(1 \dfrac{3}{5}\), ambayo inasomewa kama moja na tatu-tano.

    Nambari\(1 \dfrac{3}{5}\) inaitwa namba iliyochanganywa. Nambari iliyochanganywa ina idadi nzima na sehemu.

    Ufafanuzi: Hesabu mchanganyiko

    idadi mchanganyiko lina idadi nzima\(a\) na sehemu\(\dfrac{b}{c}\) ambapo\(c ≠ 0\). Imeandikwa kama ifuatavyo.

    \[a \dfrac{b}{c} \qquad \qquad c \neq 0\]

    Sehemu ndogo kama vile\(\dfrac{5}{4}\),\(\dfrac{3}{2}\)\(\dfrac{5}{5}\), na\(\dfrac{7}{3}\) huitwa sehemu zisizofaa. Katika sehemu isiyofaa, namba ni kubwa kuliko au sawa na denominator, hivyo thamani yake ni kubwa kuliko au sawa na moja. Wakati sehemu ina namba ambayo ni ndogo kuliko denominator, inaitwa sehemu sahihi, na thamani yake ni chini ya moja. Fractions kama vile\(\dfrac{1}{2}\)\(\dfrac{3}{7}\),, na\(\dfrac{11}{18}\) ni sehemu ndogo.

    Ufafanuzi: Vipande vilivyofaa na visivyofaa

    Sehemu\(\dfrac{a}{b}\) ni sehemu sahihi ikiwa\(a < b\) na sehemu isiyofaa ikiwa\(a ≥ b\).

    Mfano\(\PageIndex{5}\): improper fraction

    Jina sehemu isiyofaa iliyoelekezwa. Kisha kuandika sehemu isiyofaa kama namba iliyochanganywa.

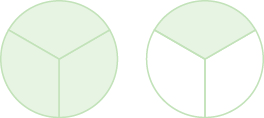
    Duru mbili zinaonyeshwa, zote mbili zimegawanywa katika vipande vitatu sawa. Mduara upande wa kushoto una vipande vyote vitatu vilivyovuliwa. Mduara upande wa kulia una kipande kimoja kivuli.

    Suluhisho

    Kila mduara umegawanywa katika vipande vitatu, hivyo kila kipande ni\(\dfrac{1}{3}\) cha mduara. Kuna vipande vinne kivuli, hivyo kuna theluthi nne au\(\dfrac{4}{3}\). Takwimu inaonyesha kwamba sisi pia tuna mduara mzima na theluthi moja, ambayo ni\(1 \dfrac{1}{3}\). Hivyo,\(\dfrac{4}{3} = 1 \dfrac{1}{3}\).

    Zoezi\(\PageIndex{9}\)

    Jina sehemu isiyofaa. Kisha uandike kama namba iliyochanganywa.

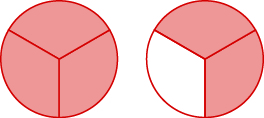
    Duru mbili zinaonyeshwa, zote mbili zimegawanywa katika vipande vitatu sawa. Mduara upande wa kushoto una vipande vyote vitatu vilivyovuliwa. Mduara upande wa kulia una vipande viwili vilivyovuliwa.

    Jibu

    \(\dfrac{5}{3}=1\dfrac{2}{3}\)

    Zoezi\(\PageIndex{10}\)

    Jina sehemu isiyofaa. Kisha uandike kama namba iliyochanganywa.

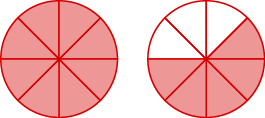
    Duru mbili zinaonyeshwa, zote mbili zimegawanywa katika vipande nane sawa. Mduara upande wa kushoto una vipande vyote nane vilivyovuliwa. Mduara upande wa kulia una vipande vitano vilivyovuliwa.

    Jibu

    \(\dfrac{13}{8}=1\dfrac{5}{8}\)

    Mfano\(\PageIndex{6}\): model a fraction

    Chora takwimu ya mfano\(\dfrac{11}{8}\).

    Suluhisho

    Denominator ya sehemu isiyofaa ni\(8\). Chora mduara umegawanywa katika vipande nane na kivuli wote. Hii inachukua huduma ya nane nane, lakini tuna\(11\) nane. Tunapaswa kivuli sehemu tatu za nane za mduara mwingine.

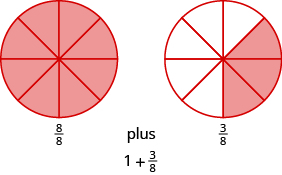
    Duru mbili zinaonyeshwa, zote mbili zimegawanywa katika vipande nane sawa. Mduara upande wa kushoto una vipande vyote nane vilivyovuliwa na huitwa kama nane ya nane. Mduara upande wa kulia una vipande vitatu vilivyovuliwa na huitwa kama themanini tatu. Mchoro unaonyesha kwamba nane nane pamoja na nane tatu ni moja pamoja na tatu nane.

    Hivyo,\(\dfrac{11}{8} = 1 \dfrac{3}{8}\).

    Zoezi\(\PageIndex{11}\)

    Chora takwimu ya mfano\(\dfrac{7}{6}\).

    Jibu

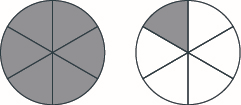
    Zoezi 4.1.11.png

    Zoezi\(\PageIndex{12}\)

    Chora takwimu ya mfano\(\dfrac{6}{5}\).

    Jibu

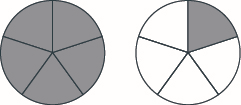
    Zoezi 4.1.12.png

    Mfano\(\PageIndex{7}\): model a fraction

    Tumia mfano wa kuandika upya sehemu isiyofaa\(\dfrac{11}{6}\) kama nambari iliyochanganywa.

    Suluhisho

    Tunaanza na\(11\) sita\(\left(\dfrac{11}{6}\right)\). Tunajua kwamba sita sita hufanya moja nzima.

    \[\dfrac{6}{6} = 1 \nonumber \]

    Hiyo inatuacha na sita zaidi ya tano, ambayo ni\(\dfrac{5}{6}\) (11 sixths minus 6 sixths ni 5 sixths). Hivyo,\(\dfrac{11}{6} = 1 \dfrac{5}{6}\).

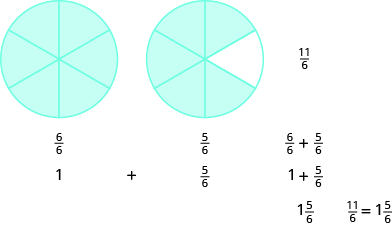
    Duru mbili zinaonyeshwa, zote mbili zimegawanywa katika vipande sita sawa. Mduara upande wa kushoto una vipande vyote sita kimvuli na kinachoitwa kama sita sita. Mduara upande wa kulia una vipande vitano kimvuli na kinachoitwa kama sita tano. Chini ya miduara, inasema moja pamoja na sita sita, kisha sita sita pamoja na sita sita sawa na sita kumi na moja, na moja pamoja na sita sita sawa na moja na sita sita. Halafu inasema kwamba kumi na moja ya sita ni sawa na sita na sita.

    Zoezi\(\PageIndex{13}\)

    Tumia mfano wa kuandika upya sehemu isiyofaa kama nambari iliyochanganywa:\(\dfrac{9}{7}\).

    Jibu

    \(1\dfrac{2}{7}\)

    Zoezi\(\PageIndex{14}\)

    Tumia mfano wa kuandika upya sehemu isiyofaa kama nambari iliyochanganywa:\(\dfrac{7}{4}\).

    Jibu

    \(1\dfrac{3}{4}\)

    Mfano\(\PageIndex{8}\): model a fraction

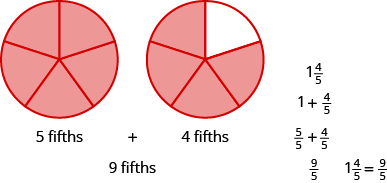
    Tumia mfano wa kuandika upya nambari iliyochanganywa\(1 \dfrac{4}{5}\) kama sehemu isiyofaa.

    Suluhisho

    Nambari iliyochanganywa\(1 \dfrac{4}{5}\) ina maana moja nzima pamoja na tano nne. Denominator ni\(5\), hivyo yote ni\(\dfrac{5}{5}\). Pamoja tano tano na tano nne ni sawa na tano tisa. Hivyo,\(1 \dfrac{4}{5} = \dfrac{9}{5}\).

    Duru mbili zinaonyeshwa, zote mbili zimegawanywa katika vipande vitano sawa. Mduara upande wa kushoto una vipande vyote vitano vilivyovuliwa na imeandikwa kama 5 tano. Mduara upande wa kulia una vipande vinne vilivyovuliwa na imeandikwa kama 4 tano. Kisha inasema kwamba 5 tano pamoja na tano 4 ni sawa na tano 9 na kwamba 9 tano ni sawa na moja pamoja na 4 tano.

    Zoezi\(\PageIndex{15}\)

    Tumia mfano wa kuandika upya nambari iliyochanganywa kama sehemu isiyofaa:\(1 \dfrac{3}{8}\).

    Jibu

    \(\dfrac{11}{8}\)

    Zoezi\(\PageIndex{16}\)

    Tumia mfano wa kuandika upya nambari iliyochanganywa kama sehemu isiyofaa:\(1 \dfrac{5}{6}\).

    Jibu

    \(\dfrac{11}{6}\)

    Badilisha kati ya vipande visivyofaa na Hesabu zilizochanganywa

    Katika Mfano\(\PageIndex{7}\), tulibadilisha sehemu\(\dfrac{11}{6}\) isiyofaa kwa nambari iliyochanganywa\(1 \dfrac{5}{6}\) kwa kutumia miduara ya sehemu. Tulifanya hivyo kwa kuungana na sita sita pamoja ili tufanye yote; ndipo tukaangalia kuona ni ngapi kati ya\(11\) vipande vilivyoachwa. Tuliona kwamba\(\dfrac{11}{6}\) alifanya kundi moja nzima ya sita sita pamoja na sita zaidi tano, kuonyesha kwamba\(\dfrac{11}{6} = \dfrac{15}{6}\).

    Maneno ya mgawanyiko\(\dfrac{11}{6}\) (ambayo yanaweza pia kuandikwa kama\(6 \overline{\smash{)}11}\)) inatuambia kujua jinsi makundi mengi ya\(6\) ni katika\(11\). Ili kubadilisha sehemu isiyofaa kwa nambari iliyochanganywa bila miduara ya sehemu, tunagawanya.

    Mfano\(\PageIndex{9}\):

    Badilisha\(\dfrac{11}{6}\) kwa nambari iliyochanganywa.

    Suluhisho

    Gawanya denominator ndani ya namba. Kumbuka\(\dfrac{11}{6}\) ina maana 11 ÷ 6.
    Tambua quotient, salio na mgawanyiko.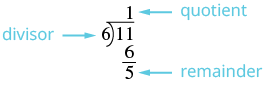
    Andika nambari iliyochanganywa kama\(quotient \dfrac{remainder}{divisor}\). \(1 \dfrac{5}{6}\)

    Hivyo,\(\dfrac{11}{6} = 1 \dfrac{5}{6}\).

    Zoezi\(\PageIndex{17}\)

    Badilisha sehemu isiyofaa kwa nambari iliyochanganywa:\(\dfrac{13}{7}\).

    Jibu

    \(1\dfrac{6}{7}\)

    Zoezi\(\PageIndex{18}\)

    Badilisha sehemu isiyofaa kwa nambari iliyochanganywa:\(\dfrac{14}{9}\).

    Jibu

    \(1\dfrac{5}{9}\)

    JINSI YA: KUBADILISHA SEHEMU ISIYOFAA KWA IDADI ILIYOCHANGANYWA

    Hatua ya 1. Gawanya denominator ndani ya namba.

    Hatua ya 2. Tambua quotient, salio, na mgawanyiko.

    Hatua ya 3. Andika nambari iliyochanganywa kama\(quotient \dfrac{remainder}{divisor}\).

    Mfano\(\PageIndex{10}\):

    Badilisha sehemu isiyofaa\(\dfrac{33}{8}\) kwa nambari iliyochanganywa.

    Suluhisho

    Gawanya denominator ndani ya namba. Kumbuka,\(\dfrac{33}{8}\) ina maana\(8 \overline{\smash{)}33}\).
    Tambua quotient, salio, na mgawanyiko.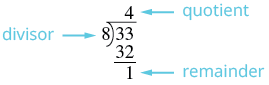
    Andika nambari iliyochanganywa kama\(quotient \dfrac{remainder}{divisor}\). \(4 \dfrac{1}{8}\)

    Hivyo,\(\dfrac{33}{8} = 4 \dfrac{1}{8}\).

    Zoezi\(\PageIndex{19}\)

    Badilisha sehemu isiyofaa kwa nambari iliyochanganywa:\(\dfrac{23}{7}\).

    Jibu

    \(3\dfrac{2}{7}\)

    Zoezi\(\PageIndex{20}\)

    Badilisha sehemu isiyofaa kwa nambari iliyochanganywa:\(\dfrac{48}{11}\).

    Jibu

    \(4\dfrac{4}{11}\)

    Katika Mfano\(\PageIndex{8}\),\(1 \dfrac{4}{5}\) tulibadilika kuwa sehemu isiyofaa kwa kwanza kuona kwamba nzima ni seti ya tano tano. Kwa hiyo tulikuwa na tano tano na tano zaidi ya tano.

    \[\dfrac{5}{5} + \dfrac{4}{5} = \dfrac{9}{5} \nonumber \]

    Wale tisa walitoka wapi? Kuna tisa ya tano, moja nzima (tano tano) pamoja na tano nne. Hebu tutumie wazo hili ili kuona jinsi ya kubadilisha nambari iliyochanganywa kwa sehemu isiyofaa.

    Mfano\(\PageIndex{11}\): convert

    Badilisha nambari iliyochanganywa\(4 \dfrac{2}{3}\) kwa sehemu isiyofaa.

    Panua idadi nzima kwa denominator. \(4 \dfrac{2}{3}\)
    Nambari nzima ni 4 na denominator ni 3.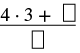
    Kurahisisha.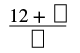
    Ongeza nambari kwa bidhaa.  
    Nambari ya nambari iliyochanganywa ni 2.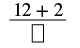
    Kurahisisha.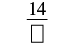
    Andika jumla ya mwisho juu ya denominator ya awali.  
    Denominator ni 3. \(\dfrac{14}{3}\)
    Zoezi\(\PageIndex{21}\)

    Badilisha nambari iliyochanganywa kwa sehemu isiyofaa:\(3 \dfrac{5}{7}\).

    Jibu

    \(\dfrac{26}{7}\)

    Zoezi\(\PageIndex{22}\)

    Badilisha nambari iliyochanganywa kwa sehemu isiyofaa:\(2 \dfrac{7}{8}\).

    Jibu

    \(\dfrac{23}{8}\)

    JINSI YA: KUBADILISHA NAMBA ILIYOCHANGANYWA KWA SEHEMU ISIYOFAA

    Hatua ya 1. Panua idadi nzima kwa denominator.

    Hatua ya 2. Ongeza nambari kwa bidhaa iliyopatikana katika Hatua ya 1.

    Hatua ya 3. Andika jumla ya mwisho juu ya denominator ya awali.

    Mfano\(\PageIndex{12}\):

    Badilisha nambari iliyochanganywa\(10 \dfrac{2}{7}\) kwa sehemu isiyofaa.

    Panua idadi nzima kwa denominator. \(10 \dfrac{2}{7}\)
    Nambari nzima ni 10 na denominator ni 7.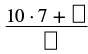
    Kurahisisha.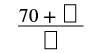
    Ongeza nambari kwa bidhaa.  
    Nambari ya nambari iliyochanganywa ni 2.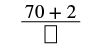
    Kurahisisha.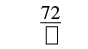
    Andika jumla ya mwisho juu ya denominator ya awali.  
    Denominator ni 7. \(\dfrac{72}{7}\)
    Zoezi\(\PageIndex{23}\)

    Badilisha nambari iliyochanganywa kwa sehemu isiyofaa:\(4 \dfrac{6}{11}\).

    Jibu

    \(\dfrac{50}{11}\)

    Zoezi\(\PageIndex{24}\)

    Badilisha nambari iliyochanganywa kwa sehemu isiyofaa:\(11 \dfrac{1}{3}\).

    Jibu

    \(\dfrac{34}{3}\)

    Wachangiaji na Majina