Skip to main content
Global

3.9: Kutatua Equations Kutumia Integers; Mali ya Idara ya Usawa (Sehemu ya 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    173352

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Kuamua kama integer ni suluhisho la equation
    • Tatua equations na integers kwa kutumia Kuongeza na Ondoa Mali ya Usawa
    • Mfano wa Mali ya Idara ya Usawa
    • Kutatua equations kutumia Mali Idara ya Usawa
    • Tafsiri kwa equation na kutatua
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Tathmini\(x + 4\) lini\(x = −4\). Ikiwa umekosa tatizo hili, kagua Mfano 3.2.9.
    2. Kutatua:\(y − 6 = 10\). Ikiwa umekosa tatizo hili, kagua Mfano 2.3.6.
    3. Tafsiri katika kujieleza algebraic\(5\) chini ya\(x\). Ikiwa umekosa tatizo hili, kagua Jedwali 1.3.1.

    Tambua Iwapo Idadi ni Suluhisho la Ulinganisho

    Katika Kutatua Equations na Ondoa na Kuongeza Mali ya Usawa, tuliona kwamba suluhisho la equation ni thamani ya kutofautiana ambayo inafanya taarifa ya kweli wakati kubadilishwa katika equation hiyo. Katika sehemu hiyo, tulipata ufumbuzi ambao ulikuwa namba nzima. Sasa kwa kuwa tumekuwa kazi na integers, tutaweza kupata ufumbuzi integer kwa equations.

    Hatua tunazochukua ili kuamua kama namba ni suluhisho la equation ni sawa kama suluhisho ni namba nzima au integer.

    JINSI YA: KUAMUA KAMA NAMBA NI Suluhisho la equation.

    Hatua ya 1. Badilisha idadi ya kutofautiana katika equation.

    Hatua ya 2. Kurahisisha maneno pande zote mbili za equation.

    Hatua ya 3. Kuamua kama equation kusababisha ni kweli.

    • Ikiwa ni kweli, nambari ni suluhisho.
    • Ikiwa si kweli, nambari sio suluhisho.
    Mfano\(\PageIndex{1}\): determine the solution

    Kuamua kama kila moja ya yafuatayo ni suluhisho la\(2x − 5 = −13\):

    1. \(x = 4\)
    2. \(x = −4\)
    3. \(x = −9\)

    Suluhisho

    (a) mbadala 4 kwa x katika equation kuamua kama ni kweli. 2x - 5 = -13
    Mbadala\(\textcolor{red}{4}\) kwa ajili ya x. \(2(\textcolor{red}{4}) - 5 \stackrel{?}{=} -13\)
    Kuzidisha. \(8 - 5 \stackrel{?}{=} -13\)
    Ondoa. \(3 \neq -13\)

    Tangu\(x = 4\) haina kusababisha equation kweli,\(4\) si ufumbuzi wa equation.

    (b) Mbadala -4 kwa x katika equation kuamua kama ni kweli. 2x - 5 = -13
    Mbadala\(\textcolor{red}{-4}\) kwa ajili ya x. \(2(\textcolor{red}{-4}) - 5 \stackrel{?}{=} -13\)
    Kuzidisha. \(-8 - 5 \stackrel{?}{=} -13\)
    Ondoa. \(-13 = -13 \; \checkmark\)

    Kwa kuwa\(x = −4\) matokeo katika equation kweli,\(−4\) ni suluhisho la equation.

    (b) Mbadala -9 kwa x katika equation kuamua kama ni kweli. 2x - 5 = -13
    Mbadala\(\textcolor{red}{-9}\) kwa ajili ya x. \(2(\textcolor{red}{-9}) - 5 \stackrel{?}{=} -13\)
    Kuzidisha. \(-18 - 5 \stackrel{?}{=} -13\)
    Ondoa. \(-23 \neq -13\)

    Tangu\(x = −9\) haina kusababisha equation kweli,\(−9\) si ufumbuzi wa equation.

    Zoezi\(\PageIndex{1}\)

    Kuamua kama kila moja ya yafuatayo ni suluhisho la\(2x − 8 = −14\):

    1. \(x = −11\)
    2. \(x = 11\)
    3. \(x = −3\)
    Jibu

    hapana

    Jibu b

    hapana

    Jibu c

    ndiyo

    Zoezi\(\PageIndex{2}\)

    Kuamua kama kila moja ya yafuatayo ni suluhisho la\(2y + 3 = −11\):

    1. \(y = 4\)
    2. \(y = −4\)
    3. \(y = −7\)
    Jibu

    hapana

    Jibu b

    hapana

    Jibu c

    ndiyo

    Kutatua Equations na Integers Kutumia Kuongeza na Ondoa Mali ya Usawa

    Katika Kutatua Equations na Ondoa na Kuongeza Mali ya Usawa, sisi kutatuliwa equations sawa na mbili inavyoonekana hapa kwa kutumia Ondoa na Kuongeza Mali ya Usawa. Sasa tunaweza kutumia tena kwa integers.

    \[\begin{split} x + 4 & = 12 \qquad \qquad \qquad y - 5 = 9 \\ x + 4 \textcolor{red}{-4} & = 12 \textcolor{red}{-4} \qquad \; \; y - 5 \textcolor{red}{+5} = 9 \textcolor{red}{+5} \\ x & = 8 \qquad \qquad \qquad \qquad \; y = 14 \end{split} \nonumber \]

    Unapoongeza au kuondoa kiasi sawa kutoka pande zote mbili za equation, bado una usawa.

    Ufafanuzi: Mali ya Usawa
    Ondoa Mali ya Usawa Kuongeza Mali ya Usawa
    Kwa idadi yoyote a, b, c, ikiwa = b kisha - c = b - c. Kwa idadi yoyote a, b, c, ikiwa = b basi a + c = b + c.
    Mfano\(\PageIndex{2}\):

    Kutatua:\(y + 9 = 5\).

    Suluhisho

    Ondoa 9 kutoka kila upande ili uondoe kuongeza. \(y + 9 \textcolor{red}{-9} = 5 \textcolor{red}{-9}\)
    Kurahisisha. \(y = -4\)

    Angalia matokeo kwa kubadili\(−4\) equation ya awali.

    Mbadala -4 kwa y \(-4 + 9 \stackrel{?}{=} 5\)
      \(5 = 5 \; \checkmark\)

    Tangu\(y = −4\) inafanya taarifa\(y + 9 = 5\) ya kweli, tuligundua ufumbuzi wa equation hii

    Zoezi\(\PageIndex{3}\)

    Kutatua:\(y + 11 = 7\)

    Jibu

    \(-4\)

    Zoezi\(\PageIndex{4}\)

    Kutatua:\(y + 15 = −4\)

    Jibu

    \(-19\)

    Mfano\(\PageIndex{3}\): solve

    Kutatua:\(a − 6 = −8\)

    Suluhisho

    Ongeza 6 kwa kila upande ili uondoe uondoaji. \(a - 6 \textcolor{red}{+6} = -8 \textcolor{red}{+6}\)
    Kurahisisha. \(a = -2\)
    Angalia matokeo kwa kubadili -2 katika equation ya awali. \(a - 6 = -8\)
    Mbadala -2 kwa. \(-2 - 6 \stackrel{?}{=} -8\)
      \(-8 = -8 \; \checkmark\)

    Suluhisho\(a − 6 = −8\) ni\(−2\). Tangu\(a = −2\) inafanya taarifa\(a − 6 = −8\) ya kweli, tuligundua ufumbuzi wa equation hii.

    Zoezi\(\PageIndex{5}\)

    Kutatua:\(a − 2 = −8\)

    Jibu

    \(-6\)

    Zoezi\(\PageIndex{6}\)

    Kutatua:\(n − 4 = −8\)

    Jibu

    \(-4\)

    Mfano wa Mali ya Idara ya Usawa

    Yote ya equations tuna kutatuliwa hadi sasa kuwa ya fomu\(x + a = b\) au\(x − a = b\). Tuliweza kutenganisha variable kwa kuongeza au kuondoa muda wa mara kwa mara. Sasa tutaweza kuona jinsi ya kutatua equations kwamba kuhusisha mgawanyiko. Sisi mfano equation na bahasha na counters katika Kielelezo\(\PageIndex{1}\).

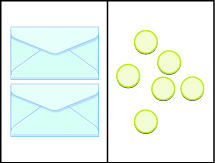
    Picha hii ina nguzo mbili. Katika safu ya kwanza ni bahasha mbili zinazofanana. Katika safu ya pili kuna miduara sita ya bluu, kuwekwa kwa nasibu.

    Kielelezo\(\PageIndex{1}\)

    Hapa, kuna bahasha mbili zinazofanana ambazo zina idadi sawa ya counters. Kumbuka, upande wa kushoto wa nafasi ya kazi lazima iwe sawa na upande wa kulia, lakini counters upande wa kushoto ni “siri” katika bahasha. Kwa hiyo ni hesabu ngapi katika kila bahasha?

    Kuamua nambari, tofauti na counters upande wa kulia katika\(2\) makundi ya ukubwa sawa. Hivyo\(6\) counters kugawanywa katika\(2\) makundi ina maana kuna lazima iwe na\(3\) counters katika kila kikundi (tangu\(6 ÷ 2 = 3\)).

    Nini equation mifano hali inavyoonekana katika Kielelezo\(\PageIndex{2}\)? Kuna bahasha mbili, na kila mmoja ana\(x\) counters. Pamoja, bahasha mbili zinapaswa kuwa na jumla ya\(6\) counters. Hivyo equation kwamba mifano ya hali ni\(2x = 6\).

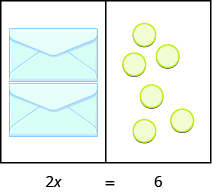
    Picha hii ina nguzo mbili. Katika safu ya kwanza ni bahasha mbili zinazofanana. Katika safu ya pili kuna miduara sita ya bluu, kuwekwa kwa nasibu. Chini ya takwimu ni mara mbili x sawa 6.

    Kielelezo\(\PageIndex{2}\)

    Tunaweza kugawanya pande zote mbili za equation na\(2\) kama tulivyofanya na bahasha na counters.

    \[\begin{split} \dfrac{2x}{\textcolor{red}{2}} & = \dfrac{6}{\textcolor{red}{2}} \\ x & = 3 \end{split} \nonumber \]

    Tuligundua kwamba kila bahasha ina\(3\) counters. Je, hii hundi? Tunajua\(2 • 3 = 6\), hivyo inafanya kazi. Hesabu tatu katika kila bahasha mbili hufanya sawa sita. Kielelezo\(\PageIndex{3}\) kinaonyesha mfano mwingine.

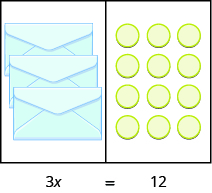
    Picha hii ina nguzo mbili. Katika safu ya kwanza ni bahasha tatu. Katika safu ya pili kuna safu nne za miduara mitatu ya bluu. Chini ya picha ni equation 3x sawa 12.

    Kielelezo\(\PageIndex{3}\)

    Sasa tuna bahasha na\(12\) counters\(3\) zinazofanana. Ni counters ngapi katika kila bahasha? Tunapaswa kutenganisha\(12\) counters katika\(3\) vikundi. Tangu\(12 ÷ 3 = 4\), kuna lazima iwe na\(4\) counters katika kila bahasha. Angalia Kielelezo\(\PageIndex{4}\).

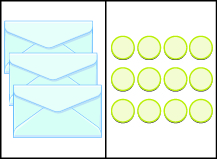
    Picha hii ina nguzo mbili. Katika safu ya kwanza ni bahasha nne. Katika safu ya pili kuna duru kumi na mbili za bluu.

    Kielelezo\(\PageIndex{4}\)

    equation kwamba mfano hali ni\(3x = 12\). Tunaweza kugawanya pande zote mbili za equation na\(3\).

    \[\begin{split} \dfrac{3x}{\textcolor{red}{3}} & = \dfrac{12}{\textcolor{red}{3}} \\ x & = 4 \end{split} \nonumber \]

    Je, hii hundi? Ni gani kwa sababu\(3 • 4 = 12\).

    Mfano\(\PageIndex{4}\): write an equation

    Andika equation inatokana na bahasha na counters, na kisha kutatua.

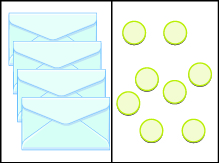
    Picha hii ina nguzo mbili. Katika safu ya kwanza ni bahasha nne. Katika safu ya pili kuna duru 8 za bluu.

    Suluhisho

    Kuna\(4\) bahasha, au maadili\(4\) haijulikani, upande wa kushoto unaofanana na\(8\) counters upande wa kulia. Hebu tupige kiasi kisichojulikana katika bahasha\(x\).

    Andika equation. \(4x = 8\)
    Gawanya pande zote mbili kwa 4. \(\dfrac{4x}{\textcolor{red}{4}} = \dfrac{8}{\textcolor{red}{4}}\)
    Kurahisisha. \(x = 2\)

    Kuna\(2\) counters katika kila bahasha.

    Zoezi\(\PageIndex{7}\)

    Andika equation inatokana na bahasha na counters. Kisha tatua.

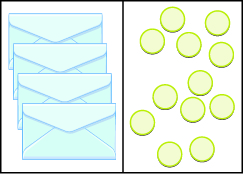
    Picha hii ina nguzo mbili. Katika safu ya kwanza ni bahasha nne. Katika safu ya pili kuna duru 12 za bluu.

    Jibu

    \(4x=12\);\(x=3\)

    Zoezi\(\PageIndex{8}\)

    Andika equation inatokana na bahasha na counters. Kisha tatua.

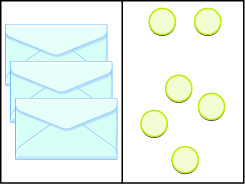
    Picha hii ina nguzo mbili. Katika safu ya kwanza ni bahasha tatu. Katika safu ya pili kuna miduara sita ya bluu.

    Jibu

    \(3x=6\);\(x=2\)

    Kutatua Equations Kutumia Mali ya Idara ya Usawa

    Mifano ya awali inaongoza kwa Idara ya Mali ya Usawa. Unapogawanya pande zote mbili za equation na nambari yoyote isiyo ya zero, bado una usawa.

    Ufafanuzi: Idara ya Mali ya Usawa

    Kwa idadi yoyote\(a, b, c\), na\(c ≠ 0\),

    \[\text{If } a = b \text{ then } \dfrac{a}{c} = \dfrac{b}{c} \ldotp\]

    Mfano\(\PageIndex{5}\): solve

    Kutatua:\(7x = −49\).

    Suluhisho

    Ili kutenganisha\(x\), tunahitaji kurekebisha kuzidisha.

    Gawanya kila upande kwa 7. \(\dfrac{7x}{\textcolor{red}{7}} = \dfrac{-49}{\textcolor{red}{7}}\)
    Rahisisha \(x = -7\)

    Angalia suluhisho.

    Mbadala -7 kwa x. \(7(-7) \stackrel{?}{=} -49\)
      \(-49 = -49 \; \checkmark\)

    Kwa hiyo,\(−7\) ni ufumbuzi wa equation.

    Zoezi\(\PageIndex{9}\)

    Kutatua:\(8a = 56\)

    Jibu

    \(7\)

    Zoezi\(\PageIndex{10}\)

    Kutatua:\(11n = 121\)

    Jibu

    \(11\)

    Mfano\(\PageIndex{6}\): solve

    Kutatua:\(−3y = 63\).

    Suluhisho

    Ili kutenganisha\(y\), tunahitaji kurekebisha kuzidisha.

    Gawanya kila upande kwa -3. \(\dfrac{-3y}{\textcolor{red}{-3}} = \dfrac{63}{\textcolor{red}{-3}}\)
    Kurahisisha. \(y = -21\)

    Angalia suluhisho.

    Mbadala -21 kwa y. \(-3(-21) \stackrel{?}{=} 63\)
      \(63 = 63 \; \checkmark\)

    Kwa kuwa hii ni kauli ya kweli,\(y = −21\) ni ufumbuzi wa equation.

    Zoezi\(\PageIndex{11}\)

    Kutatua:\(−8p = 96\)

    Jibu

    \(-12\)

    Zoezi\(\PageIndex{12}\)

    Kutatua:\(−12m = 108\)

    Jibu

    \(-9\)