3.3: Ongeza integers (Sehemu ya 1)

Malengo ya kujifunza

• Uongezekaji wa mfano wa integers
• Kurahisisha maneno na integers
• Tathmini maneno ya kutofautiana na integers
• Tafsiri misemo ya neno kwa maneno ya algebraic
• Ongeza integers katika programu

kuwa tayari!

Kabla ya kuanza, fanya jaribio hili la utayari.

1. Tathmini$x + 8$ wakati$x = 6$. Ikiwa umekosa tatizo hili, kagua Mfano 2.2.1.
2. Kurahisisha:$8 + 2(5 + 1)$. Ikiwa umekosa tatizo hili, kagua Mfano 2.1.8.
3. Tafsiri jumla ya$3$ na hasi$7$ katika kujieleza algebraic. Ikiwa umekosa tatizo hili, kagua Jedwali 2.2.3.

Uongeze wa mfano wa Integers

Sasa kwa kuwa tumeweka namba nzuri na hasi kwenye mstari wa nambari, ni wakati wa kujadili shughuli za hesabu na integers.

Wanafunzi wengi ni vizuri na kuongeza na kutoa ukweli kwa idadi chanya. Lakini kufanya kuongeza au kuondoa kwa idadi nzuri na hasi inaweza kuwa ngumu zaidi. Ugumu huu unahusiana na jinsi ubongo hujifunza.

Ubongo hujifunza vizuri kwa kufanya kazi na vitu katika ulimwengu wa kweli na kisha kuzalisha kwa dhana za abstract. Watoto hujifunza haraka kwamba ikiwa wana vidakuzi viwili na ndugu yao mkubwa anaiba moja, wana moja tu ya kushoto. Huu ni mfano halisi wa$2 − 1$. Watoto hujifunza kuongeza yao ya msingi na kutoa ukweli kutoka kwa uzoefu katika maisha yao ya kila siku. Hatimaye, wanajua ukweli wa namba bila kutegemea vidakuzi.

Kuongezea na kuondoa namba hasi zina mifano machache ya ulimwengu halisi ambayo ina maana kwetu. Walimu wa hisabati wana mbinu mbalimbali, kama vile mistari ya namba, benki, joto, na kadhalika, ili kufanya dhana hizi kuwa halisi.

Tutafanya mfano wa kuongeza na uondoaji wa hasi na counters mbili za rangi. Tunaruhusu counter ya bluu inawakilisha chanya na counter nyekundu itawakilisha hasi.

Ikiwa tuna counter moja nzuri na moja hasi, thamani ya jozi ni sifuri. Wanaunda jozi ya neutral. Thamani ya jozi hii ya neutral ni sifuri kama ilivyofupishwa kwenye Kielelezo$\PageIndex{1}$.

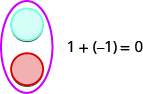
Kielelezo$\PageIndex{1}$: Counter ya bluu inawakilisha +1. Counter nyekundu inawakilisha -1. Pamoja wanaongeza sifuri.

Sisi mfano ukweli nne Aidha kwa kutumia namba$5$,$−5$ na$3$,$−3$.

$$5 + 3 \qquad −5 + (−3) \qquad −5 + 3 \qquad 5 + (−3) \nonumber$$

Mfano$\PageIndex{1}$: model the expression

Mfano:$5 + 3$.

Suluhisho

Tafsiri maneno.	5 + 3 inamaanisha jumla ya 5 na 3.
Tengeneza nambari ya kwanza. Anza na chanya 5.
Tengeneza nambari ya pili. Ongeza chanya 3.
Hesabu idadi ya hesabu.
Jumla ya 5 na 3 ni 8.	5 + 3 = 8

Zoezi$\PageIndex{1}$

Mfano wa kujieleza. $2 + 4$

Jibu

$6$

Zoezi$\PageIndex{2}$

Mfano wa kujieleza. $2 + 5$

Jibu

$7$

Mfano$\PageIndex{2}$: model the expression

Mfano:$−5 + (−3)$.

Suluhisho

Tafsiri maneno.	-5 + (-3) inamaanisha jumla ya -5 na -3.
Tengeneza nambari ya kwanza. Anza na hasi 5.
Tengeneza nambari ya pili. Ongeza hasi 3.
Hesabu idadi ya hesabu.
Jumla ya -5 na -3 ni -8.	-5 + -3 = -8

Zoezi$\PageIndex{3}$

Mfano wa kujieleza. $−2 + (−4)$

Jibu

$-6$

Zoezi$\PageIndex{4}$

Mfano wa kujieleza. $−2 + (−5)$

Jibu

$-7$

Mfano$\PageIndex{1}$ na Mfano$\PageIndex{2}$ ni sawa sana. Mfano wa kwanza unaongeza$5$ chanya na$3$ chanya - chanya zote mbili. Mfano wa pili unaongeza$5$$3$ hasi na hasi - wote hasi. Katika kila kesi, tulipata matokeo ya$8$ - ama$8$ chanya au$8$ hasi. Wakati ishara ni sawa, counters wote ni rangi sawa. Sasa hebu tuone kinachotokea wakati ishara ni tofauti.

Mfano$\PageIndex{3}$: model the expression

Mfano:$−5 + 3$.

Suluhisho

Tafsiri maneno.	-5 + 3 inamaanisha jumla ya -5 na 3.
Tengeneza nambari ya kwanza. Anza na hasi 5.
Tengeneza nambari ya pili. Ongeza chanya 3.
Ondoa jozi yoyote ya neutral.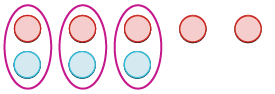
Hesabu matokeo.
Jumla ya -5 na 3 ni -2.	-5 + 3 = -2

Angalia kwamba kulikuwa na hasi zaidi kuliko chanya, hivyo matokeo ni hasi.

Zoezi$\PageIndex{5}$

Fanya mfano wa maneno, na kisha urahisishe:$2 + (-4)$

Jibu

$-2$

Zoezi$\PageIndex{6}$

Fanya mfano wa maneno, na kisha urahisishe:$2 + (−5)$

Jibu

$-3$

Mfano$\PageIndex{4}$: model the expression

Mfano:$5 + (−3)$.

Suluhisho

Tafsiri maneno.	5 + (-3) inamaanisha jumla ya 5 na -3.
Tengeneza nambari ya kwanza. Anza na chanya 5.
Tengeneza nambari ya pili. Ongeza hasi 3.
Ondoa jozi yoyote ya neutral.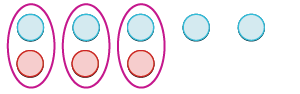
Hesabu matokeo.
Jumla ya 5 na -3 ni 2.	5 + (-3) = 2

Zoezi$\PageIndex{7}$

Fanya mfano wa maneno, na kisha urahisishe:$(−2) + 4$

Jibu

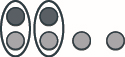
$2$

Zoezi$\PageIndex{8}$

Mfano wa maneno:$(−2) + 5$

Jibu

$3$

Mfano$\PageIndex{5}$: model the addition

Mfano kila kuongeza.

1. $4 + 2$
2. $−3 + 6$
3. $4 + (−5)$
4. $-2 + (−3)$

Suluhisho

1. $4 + 2$

Anza na chanya 4.
Ongeza chanya mbili.
Una wangapi? 6.	4 + 2 = 6

2. $−3 + 6$

Anza na hasi 3.
Ongeza chanya 6.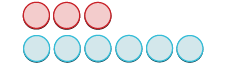
Ondoa jozi za neutral.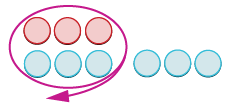
Ni wangapi wanaachwa?
3.	-3 + 6 = 3

3. $4 + (−5)$

Anza na chanya 4.
Ongeza hasi 5.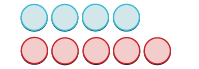
Ondoa jozi za neutral.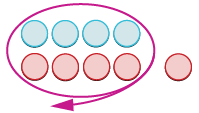
Ni wangapi wanaachwa?
-1.	4 + (-5) = -1

4. $−2 + (−3)$

Anza na hasi 2.
Ongeza hasi 3.
Una wangapi? -5.	-1 + (-3) = -5

Zoezi$\PageIndex{9}$

Mfano kila kuongeza.

1. $3 + 4$
2. $−1 + 4$
3. $4 + (−6)$
4. $−2 + (−2)$

Jibu

Jibu b

Jibu c

Jibu d

Zoezi$\PageIndex{10}$

Mfano kila kuongeza.

1. $5 + 1$
2. $−3 + 7$
3. $2 + (−8)$
4. $−3 + (−4)$

Jibu

Jibu b

Jibu c

Jibu d

Kurahisisha Maneno na Integers

Sasa kwa kuwa umeonyesha kuongeza integers ndogo nzuri na hasi, unaweza kutazama mfano katika akili yako ili kurahisisha maneno na integers yoyote.

Kwa mfano, ikiwa unataka kuongeza$37 + (−53)$, huna haja ya kuhesabu counters$37$ bluu na counters$53$ nyekundu.

Picha ya$37$ bluu counters na counters$53$ nyekundu lined up chini. Kwa kuwa kutakuwa na counters hasi zaidi kuliko counters chanya, jumla itakuwa hasi. Kwa sababu$53−37 = 16$, kuna counters$16$ zaidi hasi.

$$37 + (−53) = −16 \nonumber$$

Hebu jaribu mwingine. Tutaongeza$−74 + (−27)$. Fikiria counters$74$ nyekundu na counters$27$ zaidi nyekundu, hivyo tuna counters$101$ nyekundu wote pamoja. Hii ina maana jumla ni$−101$.

$$−74 + (−27) = −101 \nonumber$$

Angalia tena matokeo ya Mfano$\PageIndex{1}$ - Mfano$\PageIndex{2}$.

Jedwali$\PageIndex{1}$: Kuongezea kwa Integers Chanya na Hasi

5 + 3	-5 + (1-3)
wote chanya, jumla chanya	wote hasi, jumla hasi
Wakati ishara ni sawa, counters itakuwa rangi sawa, hivyo kuongeza yao.
-5 + 3	5 + (1-3)
ishara tofauti, hasi zaidi	ishara tofauti, chanya zaidi
jumla hasi	jumla chanya
Wakati ishara ni tofauti, baadhi ya counters bila kufanya jozi neutral; Ondoa kuona wangapi ni kushoto.

Mfano$\PageIndex{6}$: simplify

Kurahisisha:

1. $19 + (−47)$
2. $−32 + 40$

Suluhisho

1. Kwa kuwa ishara ni tofauti, tunaondoa$19$ kutoka$47$. Jibu litakuwa hasi kwa sababu kuna hasi zaidi kuliko chanya. $19 + (−47)=−28$
2. Ishara ni tofauti hivyo tunaondoa$32$ kutoka$40$. Jibu litakuwa chanya kwa sababu kuna chanya zaidi kuliko hasi$−32 + 40=8$

Zoezi$\PageIndex{11}$

Kurahisisha kila kujieleza:

1. $15 + (−32)$
2. $−19 + 76$

Jibu

$-17$

Jibu b

$57$

Zoezi$\PageIndex{12}$

Kurahisisha kila kujieleza:

1. $−55 + 9$
2. $43 + (−17)$

Jibu

$-46$

Jibu b

$26$

Mfano$\PageIndex{7}$: simplify

Kurahisisha:$−14 + (−36)$.

Suluhisho

Kwa kuwa ishara ni sawa, tunaongeza. Jibu litakuwa hasi kwa sababu kuna hasi tu.

$$−14 + (−36)=−50 \nonumber$$

Zoezi$\PageIndex{13}$

Kurahisisha maneno:$−31 + (−19)$

Jibu

$-50$

Zoezi$\PageIndex{14}$

Kurahisisha maneno:$−42 + (−28)$

Jibu

$-70$

Mbinu tumetumia hadi sasa kupanua kwa maneno ngumu zaidi. Kumbuka kufuata utaratibu wa shughuli.

Mfano$\PageIndex{8}$: simplify

Kurahisisha:$−5 + 3(−2 + 7)$.

Suluhisho

Kurahisisha ndani ya mabano.	-5 + 3 (5)
Kuzidisha.	-5 + 15
Ongeza kushoto kwenda kulia.	10

Zoezi$\PageIndex{15}$

Kurahisisha maneno:$−2 + 5(−4 + 7)$

Jibu

$13$

Zoezi$\PageIndex{16}$

Kurahisisha maneno:$−4 + 2(−3 + 5)$

Jibu

$0$

Wachangiaji na sifa

• Template:ContribElementaryAlgebraOpenStax