Skip to main content
Global

2.10: Kiwanda cha Waziri Mkuu na Multiple Multiple (Sehemu ya 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    173403

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Pata Multiple Multiple (LCM) ya Hesabu mbili

    Moja ya sababu tunayoangalia wingi na primes ni kutumia mbinu hizi ili kupata idadi ndogo ya kawaida ya namba mbili. Hii itakuwa na manufaa wakati sisi kuongeza na kuondoa sehemu ndogo na denominators tofauti.

    Orodha nyingi Mbinu

    Idadi ya kawaida ya namba mbili ni namba ambayo ni nyingi ya namba zote mbili. Tuseme tunataka kupata wingi wa kawaida wa 10 na 25. Tunaweza kuorodhesha virutubisho kadhaa vya kwanza vya kila nambari. Kisha tunatafuta mafungu ambayo ni ya kawaida kwa orodha zote mbili-hizi ni mafungu ya kawaida.

    \[\begin{split} 10 & \colon \; 10, 20, 30, 40, \textbf{50}, 60, 70, 80, 90, \textbf{100}, 110, \ldots \\ 25 & \colon \; 25, \textbf{50}, 75, \textbf{100}, 125, \ldots \end{split} \nonumber \]

    Tunaona kwamba\(50\) na\(100\) kuonekana katika orodha zote mbili. Wao ni wingi wa kawaida wa\(10\) na\(25\). Tungependa kupata virutubisho zaidi ya kawaida kama sisi kuendelea orodha ya mafuriko kwa kila.

    Nambari ndogo zaidi ambayo ni nyingi ya namba mbili inaitwa angalau ya kawaida nyingi (LCM). Hivyo LCM angalau ya\(10\) na\(25\) ni\(50\).

    JINSI YA: KUPATA ANGALAU KAWAIDA NYINGI (LCM) YA IDADI MBILI KWA ORODHA VINGI

    Hatua ya 1. Andika orodha kadhaa za kwanza za kila nambari.

    Hatua ya 2. Angalia kwa wingi kawaida kwa orodha zote mbili. Ikiwa hakuna mizigo ya kawaida katika orodha, weka vidokezo vya ziada kwa kila nambari.

    Hatua ya 3. Angalia kwa idadi ndogo ambayo ni ya kawaida kwa orodha zote mbili.

    Hatua ya 4. Nambari hii ni LCM.

    Mfano\(\PageIndex{5}\): lcm

    Kupata LCM ya\(15\) na\(20\) kwa orodha nyingi.

    Suluhisho

    Orodha ya kwanza mafungu kadhaa ya\(15\) na ya\(20\). Tambua mara nyingi za kwanza.

    \[\begin{split}15 & \colon \; 15, 30, 45, \textbf{60}, 75, 90, 105, 120 \\ 20 & \colon \; 20, 40, \textbf{60}, 80, 100, 120, 140, 160 \end{split} \nonumber\]

    idadi ndogo ya kuonekana katika orodha zote mbili ni\(60\), hivyo\(60\) ni angalau kawaida nyingi ya\(15\) na\(20\). Taarifa kwamba\(120\) ni katika orodha zote mbili, pia. Ni nyingi ya kawaida, lakini si angalau ya kawaida nyingi.

    Zoezi\(\PageIndex{9}\)

    Kupata angalau kawaida nyingi (LCM) ya idadi fulani:\(9\) na\(12\)

    Jibu

    \(36\)

    Zoezi\(\PageIndex{10}\)

    Kupata angalau kawaida nyingi (LCM) ya idadi fulani:\(18\) na\(24\)

    Jibu

    \(72\)

    Mambo Mkuu Method

    Njia nyingine ya kupata idadi ndogo ya kawaida ya namba mbili ni kutumia sababu zao kuu. Tutaweza kutumia njia hii ya kupata LCM ya\(12\) na\(18\).

    Tunaanza kwa kutafuta factorization mkuu wa kila idadi.

    \[12 = 2 \cdot 2 \cdot 3 \qquad \qquad 18 = 2 \cdot 3 \cdot 3 \nonumber\]

    Kisha sisi kuandika kila namba kama bidhaa ya primes, vinavyolingana primes wima iwezekanavyo.

    \[\begin{split} 12 & = 2 \cdot 2 \cdot 3 \\ 18 & = 2 \cdot \quad \; 3 \cdot 3 \end{split} \nonumber \]

    Sasa sisi kuleta chini primes katika kila safu. LCM ni bidhaa ya mambo haya.

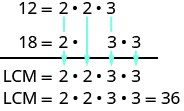
    Picha inaonyesha factorization mkuu wa 12 imeandikwa kama equation 12 sawa mara 2 mara 3. Chini equation hii ni mwingine kuonyesha factorization mkuu wa 18 imeandikwa kama equation 18 sawa 2 mara 3 mara 3. equations mbili line up wima kwa ishara sawa. Ya kwanza 2 katika factorization mkuu wa 12 inalingana na 2 katika factorization mkuu wa 18. Chini ya pili 2 katika factorization mkuu wa 12 ni pengo katika factorization mkuu wa 18. Chini ya 3 katika factorization mkuu wa 12 ni ya kwanza 3 katika factorization mkuu wa 18. Ya pili 3 katika factorization mkuu haina sababu juu yake kutoka factorization mkuu wa 12. Mstari wa usawa hutolewa chini ya factorization mkuu wa 18. Chini ya mstari huu ni equation LCM sawa na mara 2 mara 2 mara 3. Mishale ni inayotolewa chini wima kutoka factorization mkuu wa 12 kwa njia ya factorization mkuu wa 18 kuishia katika LCM equation. Mshale wa kwanza huanza saa ya kwanza 2 katika factorization mkuu wa 12 na inaendelea chini kupitia 2 katika factorization mkuu wa 18. Kumaliza na 2 ya kwanza katika LCM. Mshale wa pili huanza saa 2 ijayo katika factorization mkuu wa 12 na inaendelea chini kupitia pengo katika factorization mkuu wa 18. Kumaliza na 2 ya pili katika LCM. Mshale wa tatu huanza saa 3 katika factorization mkuu wa 12 na inaendelea chini kupitia kwanza 3 katika factorization mkuu wa 18. Kumaliza na 3 ya kwanza katika LCM. Mshale wa mwisho huanza saa ya pili ya 3 katika factorization mkuu wa 18 na inaonyesha chini ya pili 3 katika LCM.

    Kumbuka kwamba sababu kuu ya\(12\) na sababu mkuu wa\(18\) ni pamoja na katika LCM. Kwa kulinganisha juu ya primes ya kawaida, kila sababu ya kawaida ya kawaida hutumiwa mara moja tu. Hii kuhakikisha kwamba\(36\) ni angalau ya kawaida nyingi.

    JINSI YA: TAFUTA LCM KWA KUTUMIA NJIA YA MAMBO YA MKUU

    Hatua ya 1. Kupata factorization mkuu wa kila idadi.

    Hatua ya 2. Andika kila namba kama bidhaa ya primes, vinavyolingana primes wima iwezekanavyo.

    Hatua ya 3. Kuleta chini primes katika kila safu.

    Hatua ya 4. Panua mambo ya kupata LCM.

    Mfano\(\PageIndex{6}\): lcm

    Kupata LCM ya\(15\) na\(18\) kutumia mkuu sababu mbinu.

    Suluhisho

    Andika kila nambari kama bidhaa ya primes. \(15 = 3 \cdot 5 \qquad \qquad 18 = 2 \cdot 3 \cdot 3\)
    Andika kila namba kama bidhaa ya primes, vinavyolingana primes wima iwezekanavyo. \(\begin{split} 15 & = \quad \; 3 \cdot \qquad 5 \\ 18 & = 2 \cdot 3 \cdot 3 \end{split}\)
    Kuleta chini primes katika kila safu.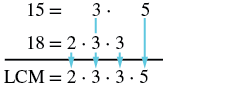
    Panua mambo ya kupata LCM.

    LCM = 2 • 3 • 3 • 5

    LCM ya 15 na 18 ni 90.
    Zoezi\(\PageIndex{11}\)

    Pata LCM kwa kutumia njia kuu ya sababu:\(15\) na\(20\)

    Jibu

    \(60\)

    Zoezi\(\PageIndex{12}\)

    Pata LCM kwa kutumia njia kuu ya sababu:\(15\) na\(35\)

    Jibu

    \(105\)

    Mfano\(\PageIndex{7}\): lcm

    Kupata LCM ya\(50\) na\(100\) kutumia mkuu sababu mbinu.

    Suluhisho

    Andika factorization mkuu wa kila idadi. \(50 = 2 \cdot 5 \cdot 5 \qquad 100 = 2 \cdot 2 \cdot 5 \cdot 5\)
    Andika kila namba kama bidhaa ya primes, vinavyolingana primes wima iwezekanavyo. \(\begin{split} 50 & = \quad \; 2 \cdot 5 \cdot 5 \\ 100 & = 2 \cdot 2 \cdot 5 \cdot 5 \end{split}\)
    Kuleta chini primes katika kila safu.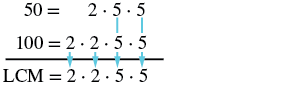
    Panua mambo ya kupata LCM.

    LCM = 2 • 2 • 5 • 5

    LCM ya 50 na 100 ni 100.
    Zoezi\(\PageIndex{13}\)

    Pata LCM kwa kutumia njia kuu ya mambo:\(55, 88\)

    Jibu

    \(440\)

    Zoezi\(\PageIndex{14}\)

    Pata LCM kwa kutumia njia kuu ya mambo:\(60, 72\)

    Jibu

    \(360\)

    Dhana muhimu

    • Pata factorization mkuu wa nambari ya composite kwa kutumia njia ya mti.
      • Pata jozi yoyote ya nambari iliyotolewa, na utumie namba hizi kuunda matawi mawili.
      • Ikiwa sababu ni mkuu, tawi hilo limekamilika. Circle mkuu.
      • Ikiwa sababu sio mkuu, uandike kama bidhaa ya jozi ya sababu na uendelee mchakato.
      • Andika nambari ya composite kama bidhaa ya primes zote zilizozunguka.
    • Pata factorization kuu ya nambari ya composite kwa kutumia njia ya ngazi.
      • Gawanya idadi kwa mkuu mdogo zaidi.
      • Kuendelea kugawa na mkuu kwamba mpaka tena mgawanyiko sawasawa.
      • Gawanya na mkuu ujao mpaka usigawanye tena sawasawa.
      • Endelea mpaka quotient ni mkuu.
      • Andika namba ya composite kama bidhaa ya primes zote pande na juu ya ngazi.
    • Kupata LCM na orodha nyingi.
      • Andika orodha kadhaa za kwanza za kila nambari.
      • Angalia kwa wingi kawaida kwa orodha zote mbili. Ikiwa hakuna mizigo ya kawaida katika orodha, weka vidokezo vya ziada kwa kila nambari.
      • Angalia kwa idadi ndogo ambayo ni ya kawaida kwa orodha zote mbili.
      • Nambari hii ni LCM.
    • Pata LCM kwa kutumia njia kuu ya mambo.
      • Kupata factorization mkuu wa kila idadi.
      • Andika kila namba kama bidhaa ya primes, vinavyolingana primes wima iwezekanavyo.
      • Kuleta chini primes katika kila safu.
      • Panua mambo ya kupata LCM.

    faharasa

    angalau ya kawaida nyingi

    Nambari ndogo zaidi ambayo ni nyingi ya namba mbili inaitwa angalau ya kawaida nyingi (LCM).

    factorization mkuu

    Factorization mkuu wa idadi ni bidhaa ya idadi ya mkuu ambayo ni sawa na idadi.

    Mazoezi hufanya kamili

    Kupata Factorization Mkuu wa Idadi Composite

    Katika mazoezi yafuatayo, pata factorization kuu ya kila nambari kwa kutumia njia ya mti wa sababu.

    1. 86
    2. 78
    3. 132
    4. 455
    5. 693
    6. 420
    7. 115
    8. 225
    9. 2475
    10. 1560

    Katika mazoezi yafuatayo, pata factorization kuu ya kila nambari kwa kutumia njia ya ngazi.

    1. 56
    2. 72
    3. 168
    4. 252
    5. 391
    6. 400
    7. 432
    8. 627
    9. 2160
    10. 2520

    Katika mazoezi yafuatayo, pata factorization kuu ya kila nambari kwa kutumia njia yoyote.

    1. 150
    2. 180
    3. 525
    4. 444
    5. 36
    6. 50
    7. 350
    8. 144

    Pata Multiple Multiple (LCM) ya Hesabu mbili

    Katika mazoezi yafuatayo, pata angalau ya kawaida (LCM) kwa kuorodhesha mizigo.

    1. 8, 12
    2. 4, 3
    3. 6, 15
    4. 12,16
    5. 30, 40
    6. 20, 30
    7. 60, 75
    8. 44, 55

    Katika mazoezi yafuatayo, pata angalau ya kawaida (LCM) kwa kutumia njia kuu ya sababu.

    1. 8, 12
    2. 12,16
    3. 24,30
    4. 28,40
    5. 70, 84
    6. 84, 90

    Katika mazoezi yafuatayo, pata angalau nyingi (LCM) kwa kutumia njia yoyote.

    1. 6, 21
    2. 9, 15
    3. 24,30
    4. 32, 40

    kila siku Math

    1. ununuzi wa vyakula Mbwa Moto huuzwa katika vifurushi vya kumi, lakini buns za mbwa wa moto huja katika pakiti za nane. Je! Ni idadi ndogo zaidi ya mbwa za moto na buns ambazo zinaweza kununuliwa ikiwa unataka kuwa na idadi sawa ya mbwa za moto na buns? (Dokezo: ni LCM!)
    2. Vyakula ununuzi Karatasi sahani zinauzwa katika paket ya 12 na vikombe chama kuja katika pakiti ya 8. Nini idadi ndogo ya sahani na vikombe unaweza kununua kama unataka kuwa na idadi sawa ya kila mmoja? (Dokezo: ni LCM!)

    Mazoezi ya kuandika

    1. Je! Unapenda kupata factorization kuu ya nambari ya composite kwa kutumia njia ya mti wa sababu au njia ya ngazi? Kwa nini?
    2. Je, ungependa kupata LCM kwa orodha nyingi au kwa kutumia njia kuu sababu? Kwa nini?

    Self Check

    (a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

    (b) Kwa ujumla, baada ya kuangalia orodha, unafikiri wewe ni vizuri tayari kwa ajili ya Sura ya? Kwa nini au kwa nini?