Skip to main content
Global

2.9: Kiwanda cha Waziri Mkuu na Multiple Multiple (Sehemu ya 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    173413

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Kupata factorization mkuu wa idadi Composite
    • Kupata angalau kawaida nyingi (LCM) ya namba mbili
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Je,\(810\) mgawanyiko na\(2, 3, 5, 6,\) au\(10\)? Ikiwa umekosa tatizo hili, kagua Mfano 2.4.5.
    2. Ni\(127\) mkuu au Composite? Ikiwa umekosa tatizo hili, kagua Mfano 2.4.8.
    3. Andika\(2 • 2 • 2 • 2\) katika nukuu ya kielelezo. Ikiwa umekosa tatizo hili, kagua Mfano 2.1.5.

    Kupata Factorization Mkuu wa Idadi Composite

    Katika sehemu iliyopita, tumegundua sababu za idadi. Nambari kuu zina sababu mbili tu, idadi\(1\) na nambari kuu yenyewe. Nambari za makundi zina mambo zaidi ya mbili, na kila nambari ya composite inaweza kuandikwa kama bidhaa ya pekee ya primes. Hii inaitwa factorization mkuu wa idadi. Wakati sisi kuandika factorization mkuu wa idadi, sisi ni kuandika upya idadi kama bidhaa ya primes. Kupata factorization mkuu wa nambari ya composite itakusaidia baadaye katika kozi hii.

    Ufafanuzi: Kiwanda cha Waziri Mkuu

    Factorization mkuu wa idadi ni bidhaa ya idadi ya mkuu ambayo ni sawa na idadi.

    Unaweza kutaka kutaja orodha ifuatayo ya idadi mkuu chini ya\(50\) kama wewe kazi kupitia sehemu hii.

    \(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47\)

    Kiwanda cha Waziri Mkuu Kutumia Njia ya Mti wa Sababu

    Njia moja ya kupata factorization mkuu wa idadi ni kufanya mti sababu. Tunaanza kwa kuandika namba, na kisha kuandika kama bidhaa ya mambo mawili. Tunaandika mambo chini ya namba na kuziunganisha kwa nambari yenye sehemu ndogo ya mstari - “tawi” la mti wa sababu.

    Ikiwa sababu ni mkuu, tunaizunguka (kama bud juu ya mti), na usijali kuwa “tawi” lolote zaidi. Ikiwa sababu sio kuu, tunarudia mchakato huu, kuandika kama bidhaa ya mambo mawili na kuongeza matawi mapya kwenye mti.

    Tunaendelea mpaka matawi yote yamekamilika na mkuu. Wakati mti wa sababu ukamilika, primes iliyozunguka hutupa factorization kuu.

    Kwa mfano, hebu kupata factorization mkuu wa\(36\). Tunaweza kuanza na jozi yoyote sababu kama vile\(3\) na\(12\). Tunaandika\(3\) na\(12\) chini\(36\) na matawi yanayounganisha.

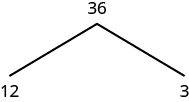
    Takwimu inaonyesha mti wa sababu na namba 36 hapo juu. Matawi mawili yanagawanyika kutoka chini ya 36. Tawi la kulia lina namba 3 mwishoni na mduara unaozunguka. Tawi la kushoto lina namba 12 mwishoni.

    Sababu\(3\) ni mkuu, kwa hiyo tunaizunguka. Sababu\(12\) ni composite, hivyo tunahitaji kupata mambo yake. Hebu tumia\(3\) na\(4\). Tunaandika mambo haya juu ya mti chini ya\(12\).

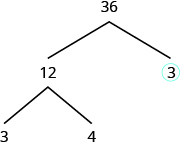
    Takwimu inaonyesha mti wa sababu na namba 36 hapo juu. Matawi mawili yanagawanyika kutoka chini ya 36. Tawi la kulia lina namba 3 mwishoni na mduara unaozunguka. Tawi la kushoto lina namba 12 mwishoni. Matawi mawili zaidi yanagawanyika kutoka chini ya 12. Tawi la kulia lina namba 4 mwishoni na tawi la kushoto lina namba 3 mwishoni.

    Sababu\(3\) ni mkuu, kwa hiyo tunaizunguka. Sababu\(4\) ni composite, na ni sababu katika\(2 • 2\). Tunaandika mambo haya chini ya\(4\). Kwa kuwa\(2\) ni mkuu, sisi mduara wote\(2s\).

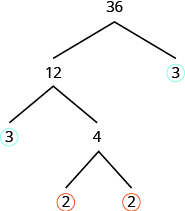
    Takwimu inaonyesha mti wa sababu na namba 36 hapo juu. Matawi mawili yanagawanyika kutoka chini ya 36. Tawi la kulia lina namba 3 mwishoni na mduara unaozunguka. Tawi la kushoto lina namba 12 mwishoni. Matawi mawili zaidi yanagawanyika kutoka chini ya 12. Tawi la kulia lina namba 4 mwishoni na tawi la kushoto lina namba 3 mwishoni na mduara unaozunguka. Matawi mawili zaidi yanagawanyika kutoka chini ya 4. Tawi la kushoto na la kulia lina namba 2 mwishoni na mduara unaozunguka.

    Factorization kuu ni bidhaa ya primes iliyozunguka. Sisi kwa ujumla kuandika factorization mkuu ili kutoka angalau kwa mkuu.

    \(2 \cdot 2 \cdot 3 \cdot 3\)

    Katika hali kama hii, ambapo baadhi ya mambo mkuu ni mara kwa mara, tunaweza kuandika factorization mkuu katika fomu kielelezo.

    \(2 \cdot 2 \cdot 3 \cdot 3\)

    \(2^{2} \cdot 3^{2}\)

    Kumbuka kwamba tunaweza kuwa na kuanza sababu mti wetu na jozi yoyote sababu ya\(36\). Tulichagua\(12\) na\(3\), lakini matokeo sawa ingekuwa sawa kama tulikuwa umeanza\(2\) na\(18\),\(4\) na\(9\), au\(6\) na\(6\).

    JINSI YA: PATA FACTORIZATION KUU YA NAMBARI YA COMPOSITE KWA KUTUMIA NJIA YA MTI
    • Hatua ya 1. Pata jozi yoyote ya nambari iliyotolewa, na utumie namba hizi kuunda matawi mawili.
    • Hatua ya 2. Ikiwa sababu ni mkuu, tawi hilo limekamilika. Circle mkuu.
    • Hatua ya 3. Ikiwa sababu sio mkuu, uandike kama bidhaa ya jozi ya sababu na uendelee mchakato.
    • Hatua ya 4. Andika nambari ya composite kama bidhaa ya primes zote zilizozunguka.
    Mfano\(\PageIndex{1}\): prime factors

    Pata factorization mkuu wa\(48\) kutumia njia ya mti wa sababu.

    Suluhisho

    Tunaweza kuanza mti wetu kwa kutumia jozi yoyote ya sababu ya 48. Hebu tumia 2 na 24. Tunazunguka 2 kwa sababu ni mkuu na hivyo tawi hilo limekamilika.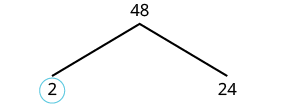
    Sasa tutazingatia 24. Hebu tumia 4 na 6.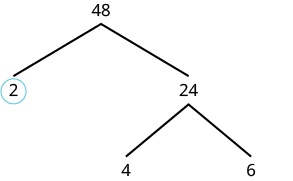

    Wala sababu ni mkuu, kwa hiyo hatuwezi kuzunguka ama. Sisi sababu 4, kwa kutumia 2 na 2. Sisi sababu 6, kwa kutumia 2 na 3.

    Sisi mduara 2s na 3 kwa kuwa wao ni mkuu. Sasa matawi yote yanaishia katika mkuu.
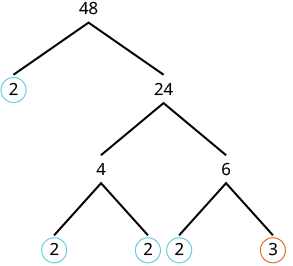    Andika bidhaa ya namba zilizozunguka. 2 • 2 • 2 • 2 • 3
    Andika kwa fomu ya kielelezo. 2 4 • 3

    Angalia hii peke yako kwa kuzidisha mambo yote pamoja. Matokeo yake yanapaswa kuwa\(48\).

    Zoezi\(\PageIndex{1}\)

    Pata factorization mkuu kwa kutumia njia ya mti wa sababu:\(80\)

    Jibu

    \(2 \cdot 2 \cdot 2 \cdot 2 \cdot 5, \text { or } 2^4 \cdot 5\)

    Zoezi\(\PageIndex{2}\)

    Pata factorization mkuu kwa kutumia njia ya mti wa sababu:\(60\)

    Jibu

    \(2 \cdot 2 \cdot 3 \cdot 5, \text { or } 2^2 \cdot 3 \cdot 5\)

    Mfano\(\PageIndex{2}\): prime factors

    Pata factorization mkuu wa\(84\) kutumia njia ya mti wa sababu.

    Suluhisho

    Tunaanza na jozi ya sababu 4 na 21. Wala sababu ni mkuu hivyo sisi sababu yao zaidi.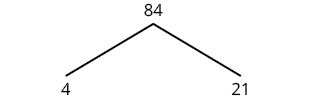
    Sasa mambo yote ni ya kwanza, kwa hiyo tunawazunguka.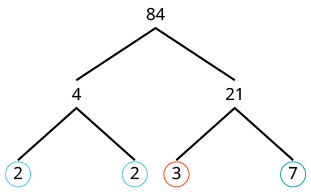
    Kisha tunaandika 84 kama bidhaa za primes zote zilizozunguka. 2 • 2 • 3 • 7 = 2 2 • 3 • 7

    Chora mti sababu ya\(84\).

    Zoezi\(\PageIndex{3}\)

    Pata factorization mkuu kwa kutumia njia ya mti wa sababu:\(126\)

    Jibu

    \(2 \cdot 3 \cdot 3 \cdot 7, \text { or } 2 \cdot 3^2 \cdot 7\)

    Zoezi\(\PageIndex{4}\)

    Pata factorization mkuu kwa kutumia njia ya mti wa sababu:\(294\)

    Jibu

    \(2 \cdot 3 \cdot 7 \cdot 7, \text { or } 2 \cdot 3 \cdot 7^2\)

    Factorization Mkuu Kutumia Njia ya Ngazi

    Njia ya ngazi ni njia nyingine ya kupata sababu kuu za nambari ya composite. Inasababisha matokeo sawa na njia ya mti wa sababu. Watu wengine wanapendelea njia ya ngazi kwa njia ya mti wa sababu, na kinyume chake.

    Kuanza kujenga “ngazi,” ugawanye nambari iliyotolewa kwa sababu yake ndogo zaidi. Kwa mfano, kuanza ngazi kwa\(36\), tunagawanya\(36\) na\(2\), sababu ndogo zaidi ya\(36\).

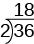
    Picha inaonyesha mgawanyiko wa 2 hadi 36 ili kupata quotient 18. Mgawanyiko huu inawakilishwa kwa kutumia mgawanyiko mabano na 2 upande wa nje wa kushoto wa mabano, 36 ndani ya mabano na 18 juu 36, nje mabano.

    Ili kuongeza “hatua” kwenye ngazi, tunaendelea kugawanya na mkuu huo mpaka haigawanyika tena sawasawa.

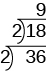
    Picha inaonyesha mgawanyiko wa 2 hadi 36 ili kupata quotient 18. Mgawanyiko huu inawakilishwa kwa kutumia mgawanyiko mabano na 2 upande wa nje wa kushoto wa mabano, 36 ndani ya mabano na 18 juu 36, nje mabano. Mwingine mgawanyiko mabano imeandikwa karibu 18 kwa 2 upande wa kushoto wa mabano na a 9 juu 18, nje ya mabano.

    Kisha tunagawanya na mkuu wa pili; hivyo\(9\) tunagawanya\(3\).

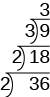
    Picha inaonyesha mgawanyiko wa 2 hadi 36 ili kupata quotient 18. Mgawanyiko huu inawakilishwa kwa kutumia mgawanyiko mabano na 2 upande wa nje wa kushoto wa mabano, 36 ndani ya mabano na 18 juu 36, nje mabano. Mwingine mgawanyiko mabano imeandikwa karibu 18 kwa 2 upande wa kushoto wa mabano na a 9 juu 18, nje ya mabano. Mwingine mgawanyiko mabano imeandikwa karibu 9 kwa 3 upande wa kushoto wa mabano na a 3 juu 9, nje ya mabano.

    Tunaendelea kugawanya ngazi kwa njia hii mpaka quotient ni mkuu. Tangu quotient\(3\),, ni mkuu, sisi kuacha hapa. Je! Unaona kwa nini njia ya ngazi wakati mwingine huitwa mgawanyiko uliowekwa?

    Factorization kuu ni bidhaa ya primes zote pande na juu ya ngazi.

    \(2 \cdot 2 \cdot 3 \cdot 3\)

    \(2^{2} \cdot 3^{2}\)

    Angalia kwamba matokeo ni sawa na tulivyopata kwa njia ya mti wa sababu.

    JINSI YA: PATA FACTORIZATION KUU YA NAMBARI YA COMPOSITE KWA KUTUMIA NJIA YA NGAZI

    Hatua ya 1. Gawanya idadi kwa mkuu mdogo zaidi.

    Hatua ya 2. Kuendelea kugawa na mkuu kwamba mpaka tena mgawanyiko sawasawa.

    Hatua ya 3. Gawanya na mkuu ujao mpaka usigawanye tena sawasawa.

    Hatua ya 4. Endelea mpaka quotient ni mkuu.

    Hatua ya 5. Andika namba ya composite kama bidhaa ya primes zote pande na juu ya ngazi.

    Mfano\(\PageIndex{3}\): prime factors

    Pata factorization kuu ya\(120\) kutumia njia ya ngazi.

    Suluhisho

    Gawanya idadi kwa mkuu mdogo, ambayo ni 2.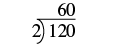
    Endelea kugawa na 2 mpaka haigawanyika tena sawasawa.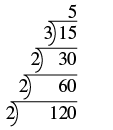
    Gawanya na mkuu ijayo, 3.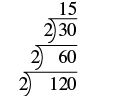
    Quotient, 5, ni mkuu, hivyo ngazi imekamilika. Andika factorization mkuu wa 120.

    2 • 2 • 2 • 3 • 5

    2 3 • 3 • 5

    Angalia hili mwenyewe kwa kuzidisha mambo. Matokeo yake yanapaswa kuwa\(120\).

    Zoezi\(\PageIndex{5}\)

    Pata factorization kuu kwa kutumia njia ya ngazi:\(80\)

    Jibu

    \(2 \cdot 2 \cdot 2 \cdot 2 \cdot 5, \text { or } 2^4 \cdot 5\)

    Zoezi\(\PageIndex{6}\)

    Pata factorization kuu kwa kutumia njia ya ngazi:\(60\)

    Jibu

    \(2 \cdot 2 \cdot 3 \cdot 5, \text { or } 2^2 \cdot 3 \cdot 5\)

    Mfano\(\PageIndex{4}\): prime factors

    Pata factorization kuu ya\(48\) kutumia njia ya ngazi.

    Suluhisho

    Gawanya idadi kwa mkuu mdogo, 2.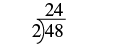
    Endelea kugawa na 2 mpaka haigawanyika tena sawasawa.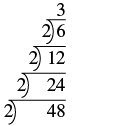
    Quotient, 3, ni mkuu, hivyo ngazi imekamilika. Andika factorization mkuu wa 48.

    \(2 • 2 • 2 • 2 • 3\)

    \(2^4 • 3\)
    Zoezi\(\PageIndex{7}\)

    Pata factorization kuu kwa kutumia njia ya ngazi:\(126\)

    Jibu

    \(2 \cdot 3 \cdot 3 \cdot 7, \text { or } 2 \cdot 3^2 \cdot 7\)

    Zoezi\(\PageIndex{8}\)

    Pata factorization kuu kwa kutumia njia ya ngazi:\(294\)

    Jibu

    \(2 \cdot 3 \cdot 7 \cdot 7, \text { or } 2 \cdot 3 \cdot 7^2\)