2.7: Kupata Mizigo na Mambo (Sehemu ya 1)

Tambua Idadi ya Idadi

Annie ni kuhesabu viatu katika chumbani yake. Viatu vinaendana kwa jozi, hivyo hawana haja ya kuhesabu kila mmoja. Anahesabu kwa wawili:$2, 4, 6, 8, 10, 12$. Ana$12$ viatu katika chumbani kwake.

Idadi$2, 4, 6, 8, 10, 12$ huitwa wingi wa$2$. Mizigo ya$2$ inaweza kuandikwa kama bidhaa ya idadi kuhesabu na$2$. Mizigo sita ya kwanza ya$2$ hutolewa hapa chini.

\[\begin{split} 1 \cdot 2 & = 2 \\ 2 \cdot 2 & = 4 \\ 3 \cdot 2 & = 6 \\ 4 \cdot 2 & = 8 \\ 5 \cdot 2 & = 10 \\ 6 \cdot 2 &= 12 \end{split} \nonumber \]

Nambari nyingi ni bidhaa ya nambari na namba ya kuhesabu. Hivyo nyingi ya$3$ itakuwa bidhaa ya idadi kuhesabu na$3$. Chini ni mafungu sita ya kwanza ya$3$.

\[\begin{split} 1 \cdot 3 & = 3 \\ 2 \cdot 3 & = 6 \\ 3 \cdot 3 & = 9 \\ 4 \cdot 3 & = 12 \\ 5 \cdot 3 & = 15 \\ 6 \cdot 3 &= 18 \end{split} \nonumber \]

Tunaweza kupata wingi wa idadi yoyote kwa kuendelea na mchakato huu. Jedwali$\PageIndex{1}$ linaonyesha wingi wa$2$ kupitia$9$ kwa namba kumi na mbili za kuhesabu kwanza.

Jedwali$\PageIndex{1}$
Idadi ya Kuhesabu	1	2	3	4	5	6	7	8	9	10	11	12
Wingi wa 2	2	4	6	8	10	12	14	16	18	20	22	24
Wingi wa 3	3	6	9	12	15	18	21	24	27	30	33	36
Wingi wa 4	4	8	12	16	20	24	28	32	36	40	44	48
Wingi wa 5	5	10	15	20	25	30	35	40	45	50	55	60
Wingi wa 6	6	12	18	24	30	36	42	48	54	60	66	72
Wingi wa 7	7	14	21	28	35	42	49	56	63	70	77	84
Wingi wa 8	8	16	24	32	40	48	56	64	72	80	88	96
Wingi wa 9	9	18	27	36	45	54	63	72	81	90	99	108

Ufafanuzi: Nyingi ya Idadi

idadi ni nyingi ya$n$ kama ni bidhaa ya idadi kuhesabu na$n$.

Kutambua ruwaza kwa wingi wa$2$$5$,$10$,, na$3$ itasaidia kwako unapoendelea katika kozi hii.

Kielelezo$\PageIndex{1}$ kinaonyesha idadi ya kuhesabu kutoka$1$ kwa$50$. Mizigo ya$2$ ni yalionyesha. Je! Unaona mfano?

$Picha inaonyesha chati yenye safu tano na nguzo kumi. Mstari wa kwanza unaorodhesha namba kutoka 1 hadi 10. Mstari wa pili unaorodhesha namba kutoka 11 hadi 20. Mstari wa tatu unaorodhesha namba kutoka 21 hadi 30. Mstari wa nne unaorodhesha namba kutoka 31 na 40. Mstari wa tano unaorodhesha namba kutoka 41 hadi 50. Sababu zote za 2 zinaonyeshwa kwa bluu.$

Kielelezo$\PageIndex{1}$: Mizigo ya 2 kati ya 1 na 50

Nambari ya mwisho ya kila nambari iliyoonyeshwa kwenye Kielelezo$\PageIndex{1}$ ni ama$0$$2$$4$,$6$,, au$8$. Hii ni kweli kwa bidhaa ya$2$ na idadi yoyote kuhesabu. Hivyo, kuwaambia kama idadi yoyote ni nyingi ya$2$ kuangalia tarakimu ya mwisho. Kama ni$0$,$2$,$4$,$6$, au$8$, basi idadi ni nyingi ya$2$.

Mfano$\PageIndex{1}$: multiples of $2$

Kuamua kama kila moja ya yafuatayo ni nyingi ya$2$:

$489$
$3,714$

Suluhisho

ni 489 nyingi ya 2?
Ni tarakimu ya mwisho 0, 2, 4, 6, au 8?	Hapana.
	489 si nyingi ya 2.

ni 3,714 nyingi ya 2?
Ni tarakimu ya mwisho 0, 2, 4, 6, au 8?	Ndiyo.
	3,714 ni nyingi ya 2.

Zoezi$\PageIndex{1}$

Kuamua kama kila idadi ni nyingi ya$2$:

$678$
$21,493$

Jibu: ndiyo
Jibu b: hapana

Zoezi$\PageIndex{2}$

Kuamua kama kila idadi ni nyingi ya$2$:

$979$
$17,780$

Jibu: hapana
Jibu b: ndiyo

Sasa hebu tuangalie wingi wa$5$. Kielelezo$\PageIndex{2}$ inaonyesha mafungu yote ya$5$ kati$1$ na$50$. Je, taarifa kuhusu wingi wa$5$?

$Picha inaonyesha chati yenye safu tano na nguzo kumi. Mstari wa kwanza unaorodhesha namba kutoka 1 hadi 10. Mstari wa pili unaorodhesha namba kutoka 11 hadi 20. Mstari wa tatu unaorodhesha namba kutoka 21 hadi 30. Mstari wa nne unaorodhesha namba kutoka 31 na 40. Mstari wa tano unaorodhesha namba kutoka 41 hadi 50. Sababu zote za 5 zinaonyeshwa kwa bluu.$

Kielelezo$\PageIndex{2}$: Mizigo ya 5 kati ya 1 na 50

Wote wingi wa$5$ mwisho na ama$5$ au$0$. Tu kama sisi kutambua wingi wa$2$ kwa kuangalia tarakimu ya mwisho, tunaweza kutambua mafungu ya$5$ kwa kuangalia tarakimu ya mwisho.

Mfano$\PageIndex{2}$: multiples of $5$

Kuamua kama kila moja ya yafuatayo ni nyingi ya$5$:

$579$
$880$

Suluhisho

Je 579 nyingi ya 5?
Je, tarakimu ya mwisho ni 5 au 0?	Hapana.
	579 si nyingi ya 5.

Je 880 nyingi ya 5?
Je, tarakimu ya mwisho ni 5 au 0?	Ndiyo.
	880 si nyingi ya 5.

Zoezi$\PageIndex{3}$

Kuamua kama kila idadi ni nyingi ya$5$.

$675$
$1,578$

Jibu: ndiyo
Jibu b: hapana

Zoezi$\PageIndex{4}$

Kuamua kama kila idadi ni nyingi ya$5$.

$421$
$2,690$

Jibu: hapana
Jibu b: ndiyo

Kielelezo$\PageIndex{3}$ inaonyesha wingi wa$10$ kati$1$ na$50$. Vipande vyote vya mwisho$10$ wote na sifuri.

$Picha inaonyesha chati yenye safu tano na nguzo kumi. Mstari wa kwanza unaorodhesha namba kutoka 1 hadi 10. Mstari wa pili unaorodhesha namba kutoka 11 hadi 20. Mstari wa tatu unaorodhesha namba kutoka 21 hadi 30. Mstari wa nne unaorodhesha namba kutoka 31 na 40. Mstari wa tano unaorodhesha namba kutoka 41 hadi 50. Sababu zote za 10 zinaonyeshwa kwa bluu.$

Kielelezo$\PageIndex{3}$: Mizigo ya 10 kati ya 1 na 50

Mfano$\PageIndex{3}$: multiples of $10$

Kuamua kama kila moja ya yafuatayo ni nyingi ya$10$:

$425$
$350$

Suluhisho

ni 425 nyingi ya 10?
Je, tarakimu ya mwisho ya sifuri?	Hapana.
	425 si nyingi ya 10.

Je 350 nyingi ya 10?
Je, tarakimu ya mwisho ya sifuri?	Ndiyo.
	350 ni nyingi ya 10.

Zoezi$\PageIndex{5}$

Kuamua kama kila idadi ni nyingi ya$10$:

$179$
$3,540$

Jibu: hapana
Jibu b: ndiyo

Zoezi$\PageIndex{6}$

Kuamua kama kila idadi ni nyingi ya$10$:

$110$
$7,595$

Jibu: ndiyo
Jibu b: hapana

Kielelezo$\PageIndex{4}$ inaonyesha mafungu ya$3$. mfano kwa wingi wa$3$ si kama dhahiri kama mwelekeo kwa wingi wa$2$,$5$, na$10$.

$Picha inaonyesha chati yenye safu tano na nguzo kumi. Mstari wa kwanza unaorodhesha namba kutoka 1 hadi 10. Mstari wa pili unaorodhesha namba kutoka 11 hadi 20. Mstari wa tatu unaorodhesha namba kutoka 21 hadi 30. Mstari wa nne unaorodhesha namba kutoka 31 na 40. Mstari wa tano unaorodhesha namba kutoka 41 hadi 50. Sababu zote za 3 zinaonyeshwa kwa bluu.$

Kielelezo$\PageIndex{4}$: Mizigo ya 3 kati ya 1 na 50

Tofauti na mifumo mingine tumekuwa kuchunguza hadi sasa, muundo huu hauhusishi tarakimu ya mwisho. mfano kwa wingi wa$3$ ni msingi wa jumla ya tarakimu. Kama jumla ya tarakimu ya idadi ni nyingi ya$3$, basi idadi yenyewe ni nyingi ya$3$. Angalia Jedwali$\PageIndex{2}$.

Jedwali$\PageIndex{2}$
Nyingi ya 3	3	6	9	12	15	18	21	24
Jumla ya tarakimu	3	6	9	1 + 2 3	1 + 5 6	1 + 8 9	2 + 1 3	2 + 4 6

Fikiria idadi$42$. Nambari ni$4$ na$2$, na jumla yao ni$4 + 2 = 6$. Kwa kuwa$6$ ni nyingi ya$3$, tunajua kwamba pia$42$ ni nyingi ya$3$.

Mfano$\PageIndex{4}$: multiples of $3$

Kuamua kama kila moja ya idadi fulani ni nyingi ya$3$:

$645$
$10,519$

Suluhisho

Ni$645$ nyingi ya$3$?

Pata jumla ya tarakimu.	6 + 4 + 5 = 15
Je 15 nyingi ya 3?	Ndiyo.
Kama sisi ni uhakika, tunaweza kuongeza tarakimu yake ili kujua. Tunaweza kuangalia kwa kugawa 645 na 3.	645 ÷ 3
Quotient ni 215.	3 • 215 = 645

Ni$10,519$ nyingi ya$3$?

Pata jumla ya tarakimu.	1 + 0 + 5 + 1 + 9 = 16
Je 15 nyingi ya 3?	Hapana.
Hivyo 10,519 si nyingi ya 3 ama..	645 ÷ 3
Tunaweza kuangalia hii kwa kugawa na 10,519 na 3.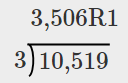

Tunapogawanya$10,519$ na$3$, hatuwezi kupata idadi ya kuhesabu, hivyo$10,519$ sio bidhaa ya namba ya kuhesabu na$3$. Si nyingi ya$3$.

Zoezi$\PageIndex{7}$

Kuamua kama kila idadi ni nyingi ya$3$:

$954$
$3,742$

Jibu: ndiyo
Jibu b: hapana

Zoezi$\PageIndex{8}$

Kuamua kama kila idadi ni nyingi ya$3$:

$643$
$8,379$

Jibu: hapana
Jibu b: ndiyo

Angalia nyuma katika chati ambapo yalionyesha wingi wa$2$, ya$5$, na ya$10$. Kumbuka kwamba wingi wa$10$ ni idadi ambayo ni mafungu ya wote$2$ na$5$. Hii ni kwa sababu$10 = 2 • 5$. Vivyo hivyo$6 = 2 • 3$, tangu, wingi wa$6$ ni namba ambazo ni nyingi za wote$2$ na$3$.

Tumia vipimo vya mgawanyiko wa kawaida

Njia nyingine ya kusema kwamba$375$ ni nyingi ya$5$ ni kusema kwamba$375$ ni mgawanyiko na$5$. Kwa kweli,$375 ÷ 5$ ni$75$, hivyo$375$ ni$5 • 75$. Taarifa katika Mfano$\PageIndex{4}$ ambayo$10,519$ si nyingi$3$. Wakati sisi kugawanywa$10,519$ na$3$ hatukupata idadi kuhesabu, hivyo$10,519$ si mgawanyiko na$3$.

Ufafanuzi: Ugawanyiko

Kama idadi$m$ ni nyingi ya$n$, basi tunasema kwamba$m$ ni mgawanyiko na$n$.

Kwa kuwa kuzidisha na mgawanyiko ni shughuli za kinyume, mifumo ya mizigo tuliyoipata inaweza kutumika kama vipimo vya ugawanyiko. Jedwali$\PageIndex{3}$ muhtasari vipimo mgawanyiko kwa baadhi ya namba kuhesabu kati ya moja na kumi.

Jedwali$\PageIndex{3}$: Vipimo vya mgawanyiko
Nambari inagawanyika na
2	ikiwa tarakimu ya mwisho ni 0, 2, 4, 6, au 8
3	ikiwa jumla ya tarakimu inagawanyika na 3
5	ikiwa tarakimu ya mwisho ni 5 au 0
6	ikiwa inagawanyika na 2 na 3
10	ikiwa tarakimu ya mwisho ni 0

Mfano$\PageIndex{5}$: divisibility

Kuamua kama$1,290$ ni mgawanyiko na$2$$3$,,$5$, na$10$.

Suluhisho

Meza$\PageIndex{4}$ inatumika vipimo mgawanyiko kwa$1,290$. Katika safu ya mbali ya kulia, tunaangalia matokeo ya vipimo vya mgawanyiko kwa kuona kama quotient ni namba nzima.

Jedwali$\PageIndex{4}$
Imegawanyika na...?	Mtihani	Kugawanyika?	Check
2	Je tarakimu ya mwisho 0, 2, 4, 6, au 8?	ndiyo	1290 ÷ 2 = 645
3	Je, jumla ya tarakimu inagawanyika na 3? 1 + 2 + 9 + 0 = 12	ndiyo	1290 ÷ 3 = 430
5	Je tarakimu ya mwisho 5 au 0?	ndiyo	1290 ÷ 5 = 258
10	Ni tarakimu ya mwisho 0?	ndiyo	1290 ÷ 10 = 129

Hivyo,$1,290$ ni mgawanyiko na$2$,$3$,$5$, na$10$.

Zoezi$\PageIndex{9}$

Kuamua kama nambari iliyotolewa inagawanyika na$2$$3$,$5$,, na$10$.

$6240$

Jibu: Inagawanyika na$2$$3$,,$5$, na$10$

Zoezi$\PageIndex{10}$

Kuamua kama nambari iliyotolewa inagawanyika na$2$$3$,$5$,, na$10$.

$7248$

Jibu: Kugawanyika$2$ na$3$, si$5$ au$10$

Mfano$\PageIndex{6}$: divisibility

Kuamua kama$5,625$ ni mgawanyiko na$2$$3$,,$5$, na$10$.

Suluhisho

Jedwali$\PageIndex{5}$ linatumika vipimo mgawanyiko$5,625$ na vipimo matokeo kwa kutafuta quotients.

Jedwali$\PageIndex{5}$
Imegawanyika na...?	Mtihani	Kugawanyika?	Check
2	Je tarakimu ya mwisho 0, 2, 4, 6, au 8?	hapana	5625 ÷ 2 = 2812.5
3	Je, jumla ya tarakimu inagawanyika na 3? 5 + 6 + 2 + 5 = 18	ndiyo	5625 ÷ 3 = 1875
5	Je tarakimu ya mwisho 5 au 0?	ndiyo	5625 ÷ 5 = 1125
10	Ni tarakimu ya mwisho 0?	hapana	5625 ÷ 10 = 562.5

Hivyo,$5,625$ ni mgawanyiko$3$ na$5$, lakini si$2$, au$10$.

Zoezi$\PageIndex{11}$

Kuamua kama nambari iliyotolewa inagawanyika na$2$$3$,$5$,, na$10$.

$4962$

Jibu: Kugawanyika na$2$$3$,, si$5$ au$10$

Zoezi$\PageIndex{12}$

Kuamua kama nambari iliyotolewa inagawanyika na$2$$3$,$5$,, na$10$.

$3765$

Jibu: Imegawanyika$3$ na$5$

Pata Mambo Yote ya Idadi

Kuna mara nyingi njia kadhaa za kuzungumza juu ya wazo moja. Hadi sasa, tumeona kwamba kama$m$ ni nyingi ya$n$, tunaweza kusema kwamba$m$ ni mgawanyiko na$n$. Tunajua kwamba$72$ ni bidhaa ya$8$ na$9$, hivyo tunaweza kusema$72$ ni nyingi ya$8$ na$72$ ni nyingi ya$9$. Tunaweza pia kusema$72$ ni mgawanyiko na$8$ na kwa$9$. Njia nyingine ya kuzungumza juu ya hili ni kusema kwamba$8$ na$9$ ni sababu za$72$. Wakati$72 = 8 ⋅ 9$ sisi kuandika tunaweza kusema kwamba tuna factored$72$.

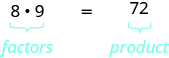
$Picha inaonyesha equation 8 mara 9 sawa 72. Ya 8 na 9 ni kinachoitwa kama sababu na 72 ni kinachoitwa bidhaa.$

Ufafanuzi: Mambo

Kama$a • b = m$, basi$a$ na$b$ ni sababu ya$m$, na$m$ ni bidhaa ya$a$ na$b$.

Katika algebra, inaweza kuwa na manufaa kuamua mambo yote ya idadi. Hii inaitwa factoring idadi, na inaweza kutusaidia kutatua aina nyingi za matatizo.

Kwa mfano, tuseme mchoreographer anapanga ngoma kwa recital ya ballet. Kuna wachezaji 24, na kwa eneo fulani, mchoreographer anataka kupanga wachezaji katika makundi ya ukubwa sawa kwenye hatua.

Kwa njia ngapi wachezaji wanaweza kuwekwa katika makundi ya ukubwa sawa? Kujibu swali hili ni sawa na kutambua mambo ya$24$. $\PageIndex{6}$Jedwali linafupisha njia tofauti ambazo mchoreographer anaweza kupanga wachezaji.

Jedwali$\PageIndex{6}$
Idadi ya Vikundi	Wachezaji kwa Kikundi	Jumla ya Wachezaji
1	24	1 • 24 = 24
2	12	2 • 12= 24
3	8	3 • 8= 24
4	6	4 • 6= 24
6	4	6 • 4= 24
8	3	8 • 3= 24
12	2	12 • 2= 24
24	1	24 • 1= 24

Je! Unaona mwelekeo gani katika Jedwali$\PageIndex{6}$? Je, taarifa kwamba idadi ya makundi mara idadi ya wachezaji kwa kila kundi daima$24$? Hii ina maana, kwa kuwa daima kuna$24$ wachezaji.

Unaweza kuona mfano mwingine ikiwa unatazama kwa makini nguzo mbili za kwanza. Nguzo hizi mbili zina seti sawa ya namba-lakini kwa utaratibu wa reverse. Wao ni vioo vya mtu mwingine, na kwa kweli, nguzo zote mbili zinaorodhesha mambo yote$24$, ambayo ni:

$1, 2, 3, 4, 6, 8, 12, 24$

Tunaweza kupata mambo yote ya idadi yoyote kuhesabu kwa utaratibu kugawa idadi kwa kila idadi kuhesabu, kuanzia na$1$. Ikiwa quotient pia ni namba ya kuhesabu, basi mgawanyiko na quotient ni sababu za idadi. Tunaweza kuacha wakati quotient inakuwa ndogo kuliko mgawanyiko.

JINSI YA: PATA MAMBO YOTE YA IDADI YA KUHESABU.

Hatua ya 1. Gawanya nambari kwa kila namba ya kuhesabu, ili, mpaka quotient ni ndogo kuliko mgawanyiko.

Ikiwa quotient ni namba ya kuhesabu, mgawanyiko na quotient ni jozi ya mambo.
Ikiwa quotient sio namba ya kuhesabu, mgawanyiko sio sababu.

Hatua ya 2. Andika orodha zote za sababu.

Hatua ya 3. Andika mambo yote ili kutoka ndogo hadi kubwa.

Mfano$\PageIndex{7}$: factors

Kupata mambo yote ya$72$.

Suluhisho

Gawanya$72$ na kila moja ya namba kuhesabu kuanzia na$1$. Ikiwa quotient ni namba nzima, mgawanyiko na quotient ni jozi ya mambo.

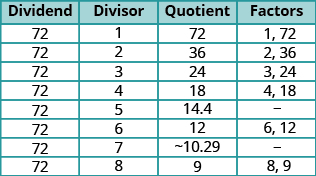
$Takwimu inaonyesha meza yenye safu kumi na nguzo nne. Mstari wa kwanza ni mstari wa kichwa na huandika safu “Mgawanyo”, “Mgawanyiko”, “Quotient”, na “Mambo”. Chini ya safu ya “Mgawanyo” safu zote zinaonyesha namba 72. Katika mstari wa pili safu ya “Mgawanyiko” ni 1, safu ya “Quotient” ni 72 na safu ya “Mambo” ni 1 na 72. Katika mstari wa tatu safu ya “Mgawanyiko” ni 2, safu ya “Quotient” ni 36 na safu ya “Mambo” ni 2 na 36. Katika mstari wa nne safu ya “Mgawanyiko” ni 3, safu ya “Quotient” ni 24 na safu ya “Mambo” ni 3 na 24. Katika mstari wa tano safu ya “Mgawanyiko” ni 4, safu ya “Quotient” ni 18 na safu ya “Mambo” ni 4 na 18. Katika mstari wa sita safu ya “Mgawanyiko” ni 5, safu ya “Quotient” ni 14.4 na safu ya “Mambo” ni tupu. Katika mstari wa saba safu ya “Mgawanyiko” ni 6, safu ya “Quotient” ni 12 na safu ya “Mambo” ni 6 na 12. Katika mstari wa nane safu ya “Mgawanyiko” ni 7, safu ya “Quotient” ni karibu 10.29 na safu ya “Mambo” ni tupu. Katika mstari wa tisa safu ya “Mgawanyiko” ni 8, safu ya “Quotient” ni 9 na safu ya “Mambo” ni 8 na 9. Katika mstari wa kumi safu ya “Mgawanyiko” ni 9, safu ya “Quotient” ni 8 na safu ya “Mambo” ni 9 na 8.$

Mstari unaofuata ingekuwa na$9$ mgawanyiko wa na quotient ya$8$. Quotient itakuwa ndogo kuliko mgawanyiko, hivyo sisi kuacha. Kama sisi kuendelea, tutakuwa kuishia tu orodha ya mambo sawa tena katika utaratibu reverse. Orodha ya mambo yote kutoka ndogo hadi kubwa$1$, tuna$2$,$3$,$4$,$6$,$8$,$9$,$12$,$18$,$24$,$36$, na$72$.

Zoezi$\PageIndex{13}$

Pata sababu zote za nambari iliyotolewa:$96$

Jibu: $1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96$

Zoezi$\PageIndex{14}$

Pata sababu zote za nambari iliyotolewa:$80$

Jibu: $1, 2, 4, 5, 8, 10, 16, 20, 40, 80$