Skip to main content
Global

2.6: Kutatua Equations Kutumia Ondoa na Kuongeza Mali ya Usawa (Sehemu ya 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    173394

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Tafsiri Maneno ya Neno kwa Equations Algebraic

    Kumbuka, equation ina ishara sawa (\(=\)) kati ya maneno mawili ya algebraic. Hivyo kama tuna sentensi kwamba inatuambia kwamba maneno mawili ni sawa, tunaweza kutafsiri katika equation. Tunatafuta maneno ya kidokezo ambayo inamaanisha sawa. Maneno mengine yanayotafsiri kwa ishara sawa ni:

    • ni sawa na
    • ni sawa na
    • ni
    • anatoa
    • ilikuwa
    • itakuwa

    Inaweza kuwa na manufaa kuweka sanduku karibu na neno (s) sawa katika sentensi ili kukusaidia kuzingatia tofauti juu ya kila maneno. Kisha kutafsiri kila maneno kwa maneno, na uandike kila upande wa ishara sawa.

    Tutafanya mazoezi ya kutafsiri sentensi za neno katika milinganyo ya algebraic. Baadhi ya hukumu itakuwa idadi ya msingi ukweli na hakuna vigezo kutatua kwa. Baadhi ya sentensi kutafsiri katika equations na vigezo. Lengo sasa hivi ni kutafsiri maneno katika algebra.

    Mfano\(\PageIndex{8}\): translate

    Tafsiri sentensi katika equation algebraic: Jumla ya\(6\) na\(9\) ni\(15\).

    Suluhisho

    Neno ni inatuambia ishara sawa huenda kati\(9\) na\(15\).

    Pata neno “sawa”. Jumla ya 6 na 9 ni 15
    Andika ishara =. Jumla ya 6 na 9 = 15
    Tafsiri maneno upande wa kushoto wa neno sawa katika kujieleza algebraic. 6 + 9 = _____
    Tafsiri maneno kwa haki ya neno sawa katika kujieleza algebraic. 6 + 9 = 15
    Zoezi\(\PageIndex{15}\)

    Tafsiri sentensi katika equation algebraic: Jumla ya\(7\) na\(6\) anatoa\(13\).

    Jibu

    \(7+6=13\)

    Zoezi\(\PageIndex{16}\)

    Tafsiri sentensi katika equation algebraic: Jumla ya\(8\) na\(6\) ni\(14\).

    Jibu

    \(8+6=14\)

    Mfano\(\PageIndex{9}\): translate

    Tafsiri sentensi katika equation algebraic: bidhaa ya\(8\) na\(7\) ni\(56\).

    Suluhisho

    Eneo la neno linatuambia kwamba ishara sawa inakwenda kati\(7\) na\(56\).

    Pata neno “sawa”. Bidhaa ya 8 na 7 ni 56
    Andika ishara =. Bidhaa ya 8 na 7 = 56
    Tafsiri maneno upande wa kushoto wa neno sawa katika kujieleza algebraic. 8 • 7 = _____
    Tafsiri maneno kwa haki ya neno sawa katika kujieleza algebraic. 8 • 7 = 56
    Zoezi\(\PageIndex{17}\)

    Tafsiri sentensi katika equation algebraic: bidhaa ya\(6\) na\(9\) ni\(54\).

    Jibu

    \(6\cdot 9 = 54\)

    Zoezi\(\PageIndex{18}\)

    Tafsiri sentensi katika equation algebraic: bidhaa ya\(21\) na\(3\) anatoa\(63\).

    Jibu

    \(21\cdot 3 = 63\)

    Mfano\(\PageIndex{10}\): translate

    Tafsiri sentensi katika equation algebraic: Mara mbili tofauti ya\(x\) na\(3\) anatoa\(18\).

    Suluhisho

    Pata neno “sawa”.
    Tambua maneno muhimu: mara mbili; tofauti ya... na... Mara mbili ina maana mara mbili.
    Tafsiri.
    Zoezi\(\PageIndex{19}\)

    Tafsiri sentensi iliyotolewa katika equation algebraic: Mara mbili tofauti ya\(x\) na\(5\) anatoa\(30\).

    Jibu

    \(2(x-5)=30\)

    Zoezi\(\PageIndex{20}\)

    Tafsiri sentensi iliyotolewa katika equation algebraic: Mara mbili tofauti ya\(y\) na\(4\) anatoa\(16\).

    Jibu

    \(2(y-4)=16\)

    Tafsiri kwa Equation na Kutatua

    Sasa hebu tufanye mazoezi ya kutafsiri sentensi katika equations algebraic na kisha kutatua yao. Tutatatua equations kwa kutumia Ondoa na Kuongeza Mali ya Usawa.

    Mfano\(\PageIndex{11}\): translate and solve

    Tafsiri na kutatua: Tatu zaidi\(x\) ya ni sawa na\(47\).

    Suluhisho

      Tatu zaidi ya x ni sawa na 47.
    Tafsiri. \(x + 3 = 47\)
    Ondoa 3 kutoka pande zote mbili za equation. \(x + 3 \textcolor{red}{-3} = 47 \textcolor{red}{-3}\)
    Rahisisha \(x = 44\)
    Tunaweza kuangalia. Hebu x = 44. \(44 + 3 \stackrel{?}{=} 47\)
      \(47 = 47 \; \checkmark\)

    Hivyo\(x = 44\) ni suluhisho.

    Zoezi\(\PageIndex{21}\)

    Tafsiri na kutatua: Saba zaidi\(x\) ya ni sawa na\(37\).

    Jibu

    \(x + 7 = 37; x = 30\)

    Zoezi\(\PageIndex{22}\)

    Tafsiri na kutatua: Eleven zaidi\(y\) ya ni sawa na\(28\).

    Jibu

    \(y + 11 = 28; y = 17\)

    Mfano\(\PageIndex{12}\): translate and solve

    Tafsiri na kutatua: tofauti ya\(y\) na\(14\) ni\(18\).

    Suluhisho

      Tofauti ya y na 14 ni 18.
    Tafsiri. \(y - 14 = 18\)
    Ongeza 14 kwa pande zote mbili. \(y - 14 \textcolor{red}{+14} = 18 \textcolor{red}{+14}\)
    Kurahisisha. \(y = 32\)
    Tunaweza kuangalia. Hebu y = 32. \(32 - 14 \stackrel{?}{=} 18\)
      \(18 = 18 \; \checkmark\)

    Hivyo\(y = 32\) ni suluhisho.

    Zoezi\(\PageIndex{23}\)

    Tafsiri na kutatua: Tofauti ya\(z\) na\(17\) ni sawa na\(37\).

    Jibu

    \(z - 17 = 37; z = 54\)

    Zoezi\(\PageIndex{24}\)

    Tafsiri na kutatua: Tofauti ya\(x\) na\(19\) ni sawa na\(45\).

    Jibu

    \(x - 19 = 45; x = 64\)

    Dhana muhimu

    • Kuamua kama idadi ni suluhisho la equation.
      1. Badilisha idadi ya kutofautiana katika equation.
      2. Kurahisisha maneno pande zote mbili za equation.
      3. Kuamua kama equation kusababisha ni kweli. Ikiwa ni kweli, nambari ni suluhisho.
      Ikiwa si kweli, nambari sio suluhisho.
    • Ondoa Mali ya Usawa
      • Kwa idadi yoyote\(a\),\(b\), na\(c\),
    • Kutatua equation kwa kutumia Ondoa Mali ya Usawa.
      1. Tumia Mali ya Kuondoa ya Usawa ili kutenganisha kutofautiana.
      2. Kurahisisha maneno pande zote mbili za equation.
      3. Angalia suluhisho.
    • Kuongeza Mali ya Usawa
      • Kwa idadi yoyote\(a\),\(b\), na\(c\),
    • Tatua equation kwa kutumia Mali ya Kuongeza ya Usawa.
      1. Tumia Mali ya Kuongeza ya Usawa ili kutenganisha kutofautiana.
      2. Kurahisisha maneno pande zote mbili za equation.
      3. Angalia suluhisho.

    faharasa

    ufumbuzi wa equation

    Suluhisho la equation ni thamani ya kutofautiana ambayo inafanya taarifa ya kweli wakati kubadilishwa katika equation. Mchakato wa kutafuta suluhisho la equation inaitwa kutatua equation.

    Mazoezi hufanya kamili

    Tambua Iwapo Idadi ni Suluhisho la Ulinganisho

    Katika mazoezi yafuatayo, onyesha kama kila thamani iliyotolewa ni suluhisho la equation.

    1. x + 13 = 21
      1. x = 8
      2. x = 34
    2. y + 18 = 25
      1. y = 7
      2. y = 43
    3. m - 4 = 13
      1. m = 9
      2. m = 17
    4. n - 9 = 6
      1. n = 3
      2. n = 15
    5. 3p + 6 = 15
      1. p = 3
      2. p = 7
    6. 8q + 4 = 20
      1. q = 2
      2. q = 3
    7. 18d - 9 = 27
      1. d = 1
      2. d = 2
    8. 24 f - 12 = 60
      1. f = 2
      2. f = 3
    9. 8u - 4 = 4u + 40
      1. u = 3
      2. u = 11
    10. 7v - 3 = 4v + 36
      1. v = 3
      2. v = 11
    11. 20h - 5 = 15h + 35
      1. h = 6
      2. h = 8
    12. 18k - 3 = 12k + 33
      1. k = 1
      2. k = 6

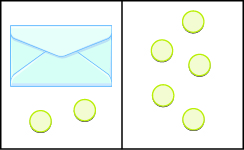
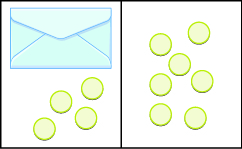
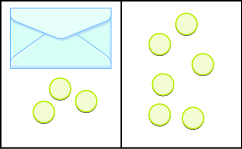
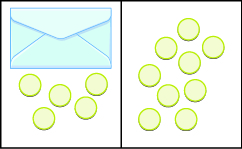
    Mfano wa Mali ya Kutoa ya Usawa

    Katika mazoezi yafuatayo, andika equation inayotokana na bahasha na counters na kisha kutatua kutumia mali ya kuondoa ya usawa.

    1. Picha imegawanywa kwa nusu vertically. Kwenye upande wa kushoto ni bahasha yenye counters 2 chini yake. Kwenye upande wa kulia ni counters 5.
    2. Picha imegawanywa kwa nusu vertically. Kwenye upande wa kushoto ni bahasha yenye counters 4 chini yake. Kwenye upande wa kulia ni counters 7.
    3. Picha imegawanywa kwa nusu vertically. Kwenye upande wa kushoto ni bahasha yenye counters tatu chini yake. Kwenye upande wa kulia ni counters 6.
    4. Picha imegawanywa kwa nusu vertically. Kwenye upande wa kushoto ni bahasha yenye counters 5 chini yake. Kwenye upande wa kulia ni counters 9.

    Kutatua Equations kwa kutumia Ondoa Mali ya Usawa

    Katika mazoezi yafuatayo, tatua kila equation kwa kutumia mali ya kuondoa ya usawa.

    1. a + 2 = 18
    2. b + 5 = 13
    3. p + 18 = 23
    4. q + 14 = 31
    5. r + 76 = 100
    6. s + 62 = 95
    7. 16 = x + 9
    8. 17 = y + 6
    9. 93 = p + 24
    10. 116 = q + 79
    11. 465 = d + 398
    12. 932 = c + 641

    Kutatua Equations kwa kutumia Mali ya Kuongeza ya Usawa

    Katika mazoezi yafuatayo, tatua kila equation kwa kutumia mali ya kuongeza ya usawa.

    1. y - 3 = 19
    2. x - 4 = 12
    3. u - 6 = 24
    4. v - 7 = 35
    5. f - 55 = 123
    6. g - 39 = 117
    7. 19 = n - 13
    8. 18 = m - 15
    9. 10 = p - 38
    10. 18 = q - 72
    11. 268 = y - 199
    12. 204 = z - 149

    Tafsiri maneno ya Neno kwa Equations Algebraic

    Katika mazoezi yafuatayo, tafsiri sentensi iliyotolewa katika equation algebraic.

    1. Jumla ya 8 na 9 ni sawa na 17.
    2. Jumla ya 7 na 9 ni sawa na 16.
    3. Tofauti ya 23 na 19 ni sawa na 4.
    4. Tofauti ya 29 na 12 ni sawa na 17.
    5. Bidhaa ya 3 na 9 ni sawa na 27.
    6. Bidhaa ya 6 na 8 ni sawa na 48.
    7. Quotient ya 54 na 6 ni sawa na 9.
    8. Quotient ya 42 na 7 ni sawa na 6.
    9. Mara mbili tofauti ya n na 10 inatoa 52.
    10. Mara mbili tofauti ya m na 14 inatoa 64.
    11. Jumla ya mara tatu y na 10 ni 100.
    12. Jumla ya mara nane x na 4 ni 68.

    Tafsiri kwa Equation na Kutatua

    Katika mazoezi yafuatayo, tafsiri sentensi iliyotolewa katika equation algebraic na kisha kutatua.

    1. Tano zaidi ya p ni sawa na 21.
    2. Tisa zaidi ya q ni sawa na 40.
    3. Jumla ya r na 18 ni 73.
    4. Jumla ya s na 13 ni 68.
    5. Tofauti ya d na 30 ni sawa na 52.
    6. Tofauti ya c na 25 ni sawa na 75.
    7. 12 chini ya u ni 89.
    8. 19 chini ya w ni 56.
    9. 325 chini ya c anatoa 799.
    10. 299 chini ya d anatoa 850.

    kila siku Math

    1. Bima Vince ya gari bima ina $500 GNU. Pata kiasi ambacho kampuni ya bima italipa, p, kwa madai ya $1800 kwa kutatua equation 500 + p = 1800.
    2. Bima Marta ya mmiliki wa nyumba sera ya bima ina $750 GNU. Kampuni ya bima ililipa $5800 ili kutengeneza uharibifu uliosababishwa na dhoruba. Pata gharama ya jumla ya uharibifu wa dhoruba, d, kwa kutatua equation d -750 = 5800.
    3. Sale kununua Arthur kununuliwa suti kwamba alikuwa kuuzwa kwa $120 off. Alilipa $340 kwa suti. Pata bei ya awali, p, ya suti kwa kutatua equation p -120 = 340.
    4. Uuzaji wa ununuzi Rita alinunua sofa iliyokuwa ikiuzwa kwa $1299. Alilipa jumla ya $1409, ikiwa ni pamoja na kodi ya mauzo. Pata kiasi cha kodi ya mauzo, t, kwa kutatua equation 1299 + t = 1409.

    Mazoezi ya kuandika

    1. Je, x = 1 ni suluhisho la equation 8x - 2 = 16 ÷ 6x? Unajuaje?
    2. Andika equation y - 5 = 21 kwa maneno. Kisha kufanya juu ya tatizo neno kwa equation hii.

    Self Check

    (a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

    (b) Orodha hii inakuambia nini kuhusu ustadi wako wa sehemu hii? Ni hatua gani utachukua ili kuboresha?